1.3. Основные виды связей

Помимо заданных – активных сил – на тело, равновесие которого рассматривается, действуют силы, приложенные со стороны опор – связей. Реакция связи потому так и называется потому, что возникает в ответ – реагирует на действие сил, приложенных к телу. В зависимости от устройства связи обладают различными возможностями по ограничению перемещения точки закрепления.

Рассмотрим некоторые из так называемых идеальных связей. Понятие идеальных связей – важнейшее понятие механики будет подробно рассмотрено в дальнейшем при изучении аналитической механики. Пока будем считать связь идеальной, если возможно не учитывать явление трения.

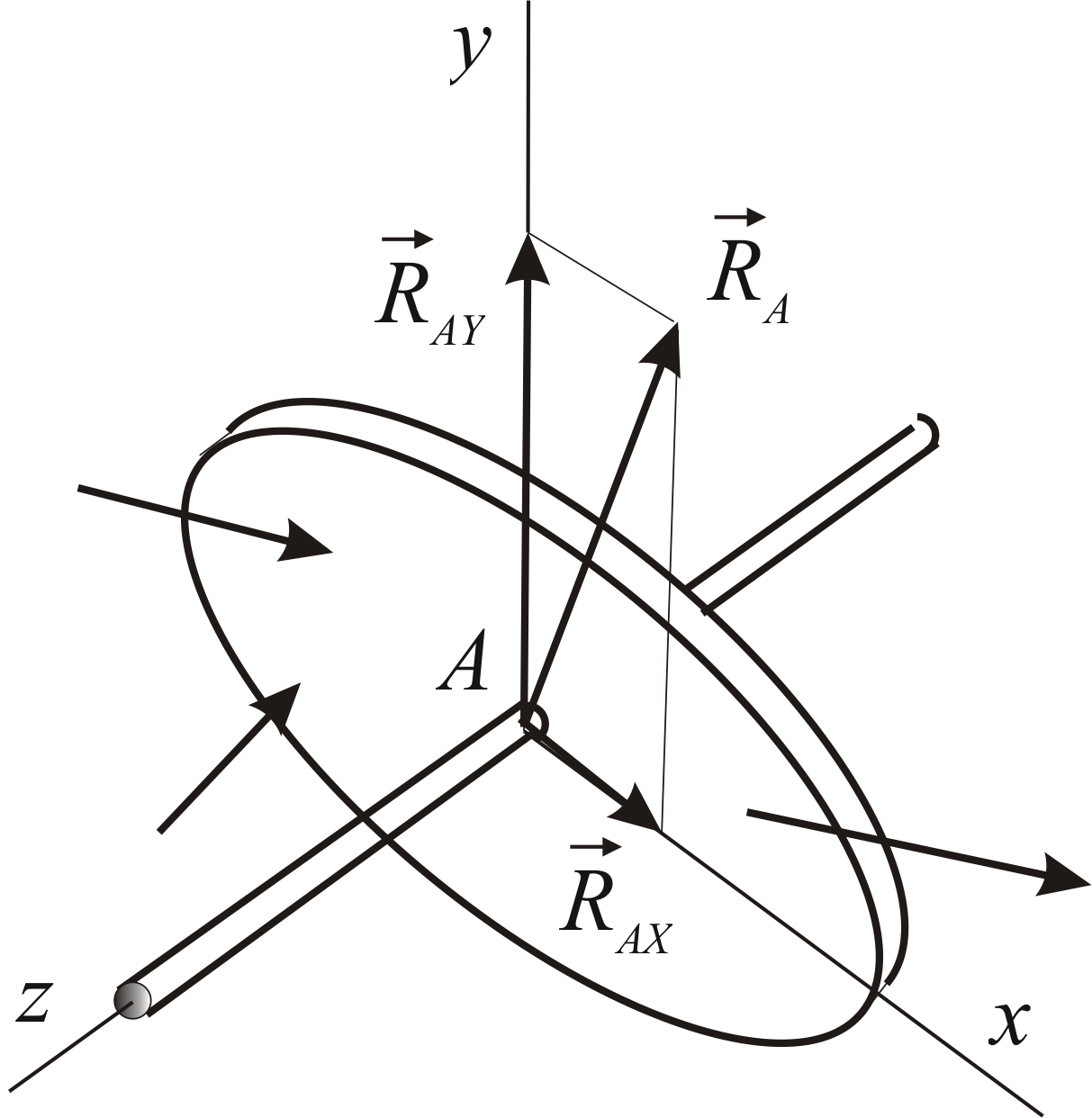
Одна из самых распространённых опор – неподвижный цилиндрический шарнир (подшипник). Простейшую схему такой опоры можно представить следующим образом: имеется закреплённый стержень, на который надета пластина (Рис. 1.4). Такая опора позволяет пластине скользить вдоль стержня и вращаться вокруг него. Под действием активной нагрузки возникает точечный контакт между стержнем и пластиной. Реакция направлена по нормали к стержню (оси шарнира), но заранее неизвестно в какой точке осуществляется контакт и, следовательно, по какой из нормалей к оси шарнира будет направлена реакция.

Рис. 1.4		Рис.1.5

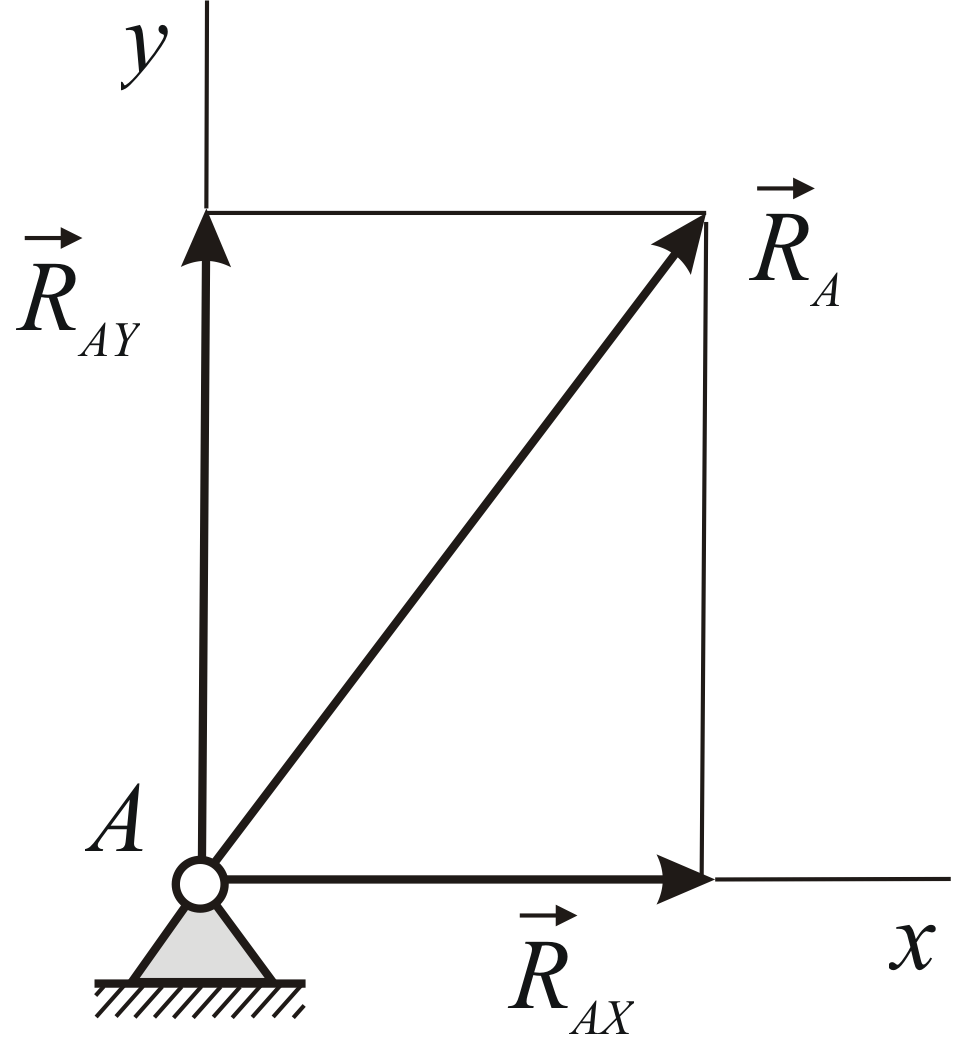
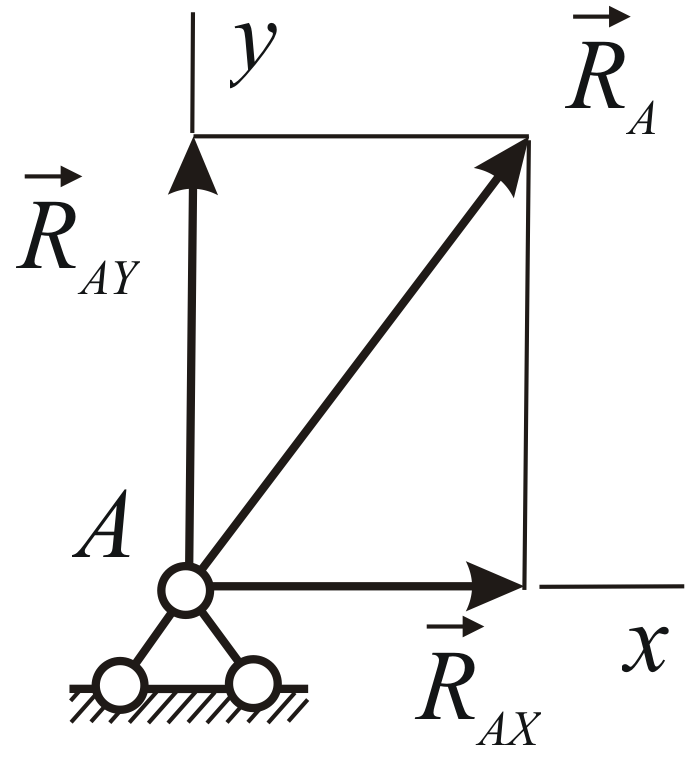
Таким образом, в общем случае реакция неподвижного шарнира расположена в плоскости, перпендикулярной оси шарнира, но в этой плоскости она заранее неизвестна ни по модулю, ни по направлению. Для её определения удобно ввести две неизвестные по модулю составляющие, направленные параллельно координатным осям в положительном направлении этих осей и. Неизвестными величинами в таком случае будут проекции силы реакции шарнира на координатные осии.

Размерами шарнира при расчётах пренебрегают. Схематическое изображение неподвижного шарнира представлено на Рис. 1.5. Конструктивно неподвижный цилиндрический шарнир, как правило, представляет собой шарикоподшипник.

Для некоторых видов опор перемещения точки закрепления ограничиваются только в определённом направлении. По этому направлению и действует сила реакции связей. В качестве неизвестной величины для опор такого типа имеет смысл рассматривать модуль реакции опоры.

Рассмотрим опоры, относящиеся к такому типу.

Гибкая невесомая нерастяжимая нить.Нить не даёт телу перемещаться в единственном направлении – вдоль нити от точки закрепления (на растяжение нити). Реакция такой нитивсегда направлена вдоль нити к точке подвеса (Рис.1.6).

Рис. 1.6		Рис. 1.7

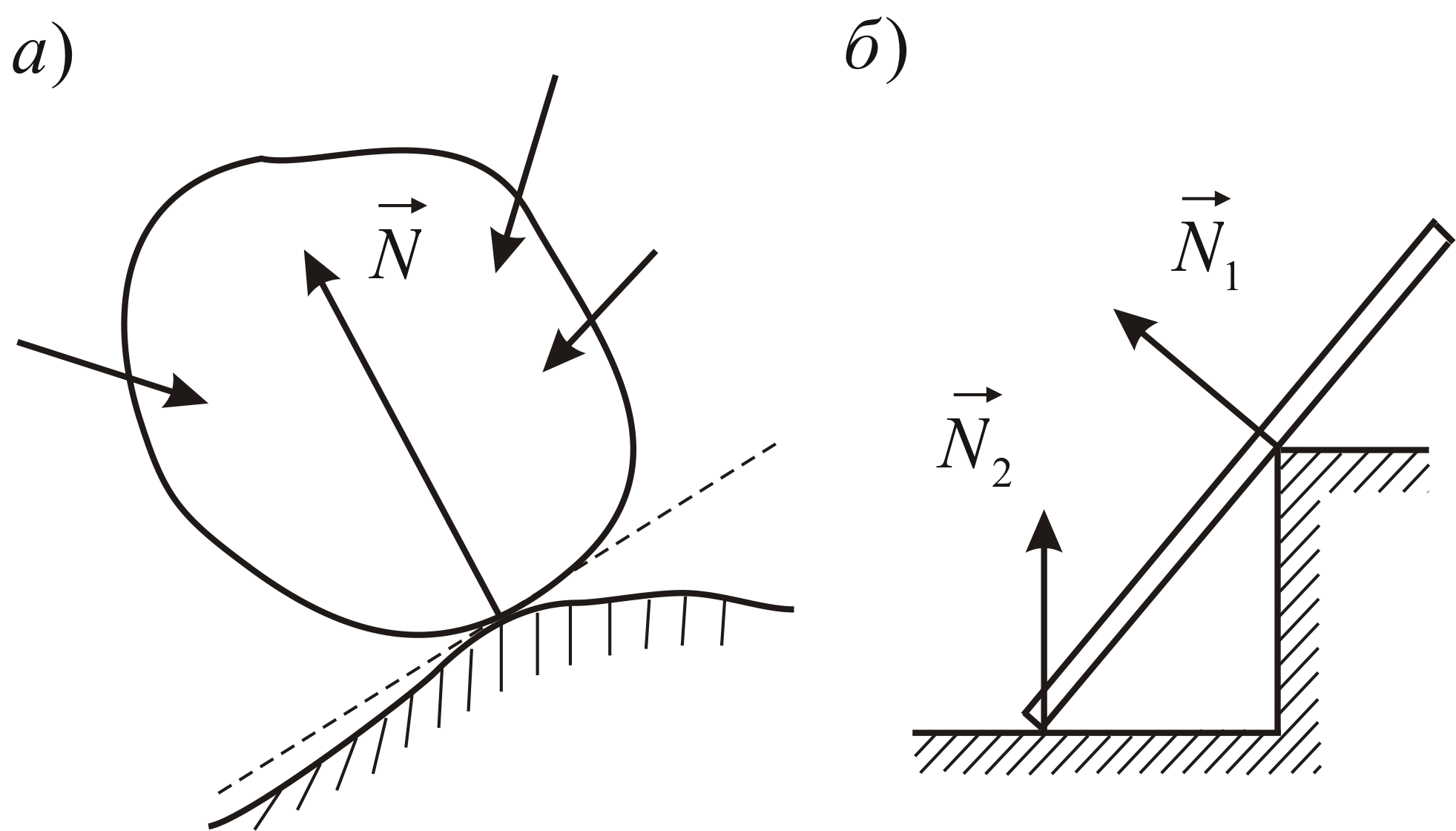
Гладкая (без трения) поверхность.Реакция такой поверхности направлена по общей нормали к поверхностям тел, проведённой в точке контакта, причём наружу от опорной поверхности (Рис.1.7а). Если в точке контакта у одной из поверхностей нормаль не определена (Рис.1.7б), то реакция направлена по нормали к другой поверхности.

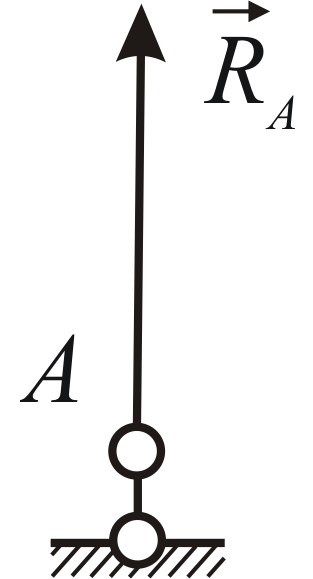
Невесомый ненагруженный стержень с шарнирно закреплёнными концами. Пусть тело закреплено при помощи неподвижного шарнираи невесомого стержня, шарнирно закреплённого на концах (Рис. 1.8).

Рассмотрим стержень (Рис.1.9). Он находится в равновесии под действием двух сил, приложенных в точкахи. Две силы могут уравновесить друг друга только в том случае, когда они действуют по одной прямой. Таким образом, сила давления тела на стерженьнаправлена вдоль стержня. Учитывая третий закон Ньютона, приходим к выводу, что реакция ненагруженного стержня направлена вдоль прямой, соединяющей шарнирно закреплённые концы стержня.

Рис. 1.8		Рис. 1.9.

Схематическое изображение такой опоры и её реакция представлены на Рис.1.10.

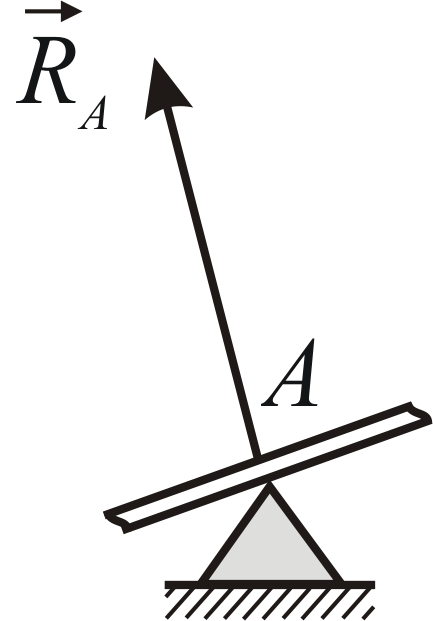
Подвижный цилиндрический шарнирпредставляет собой цилиндрический шарнир, поставленный на катки, на которых он может без сопротивления перемещаться по опорной поверхности. Реакция направлена по нормали к опорной поверхности (Рис.1.11).

Рис.1.10		Рис.1.11		Рис.1.12		Рис.1.13		Рис.1.14

Аналогичные реакции возникают в шарнирно-скользящейопоре (Рис.1.12) иигольчатойопоре (Рис.1.13).

Заметим, что шарнирно-неподвижную опору (Рис.1.5) можно представить как систему двух шарнирно закреплённых на концах стержней (Рис.1.14).

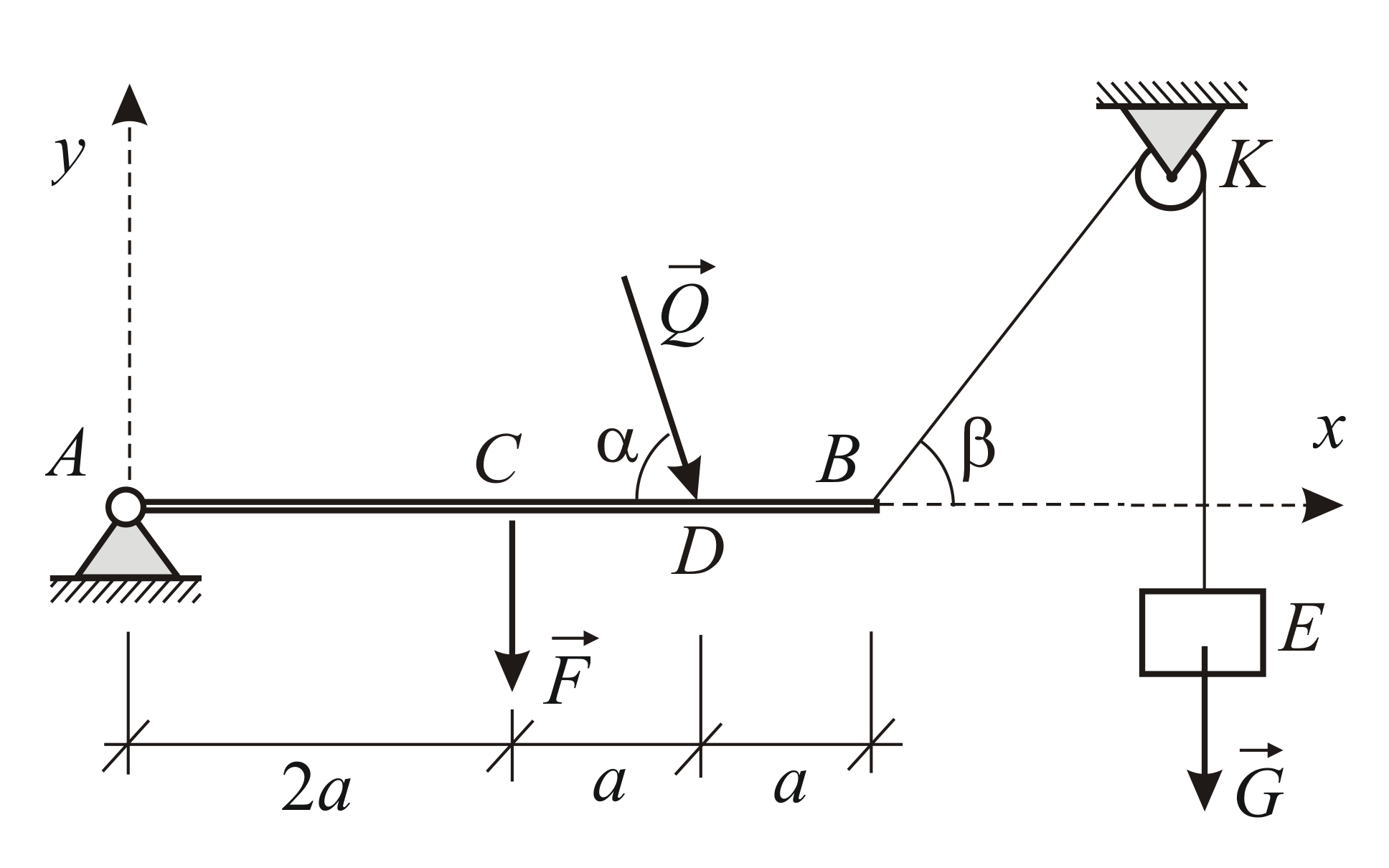
Пример 1.1

Балка имеет шарнирно неподвижную опору в точкеи прикреплена к концу троса в точке. Балка нагружена силамии, приложенными как показано на Рис. 1.15. Трос переброшен через блоки растягивается противовесом. Пренебрегая трением на блоке, определить силу реакции шарнираи силу тяжестипротивовеса.

Дано:

Рассмотрим равновесие стержня . Кроме заданных сили, на балку действуют сила реакции троса , приложенная в точке, и сила реакции шарнира, приложенная в точке.

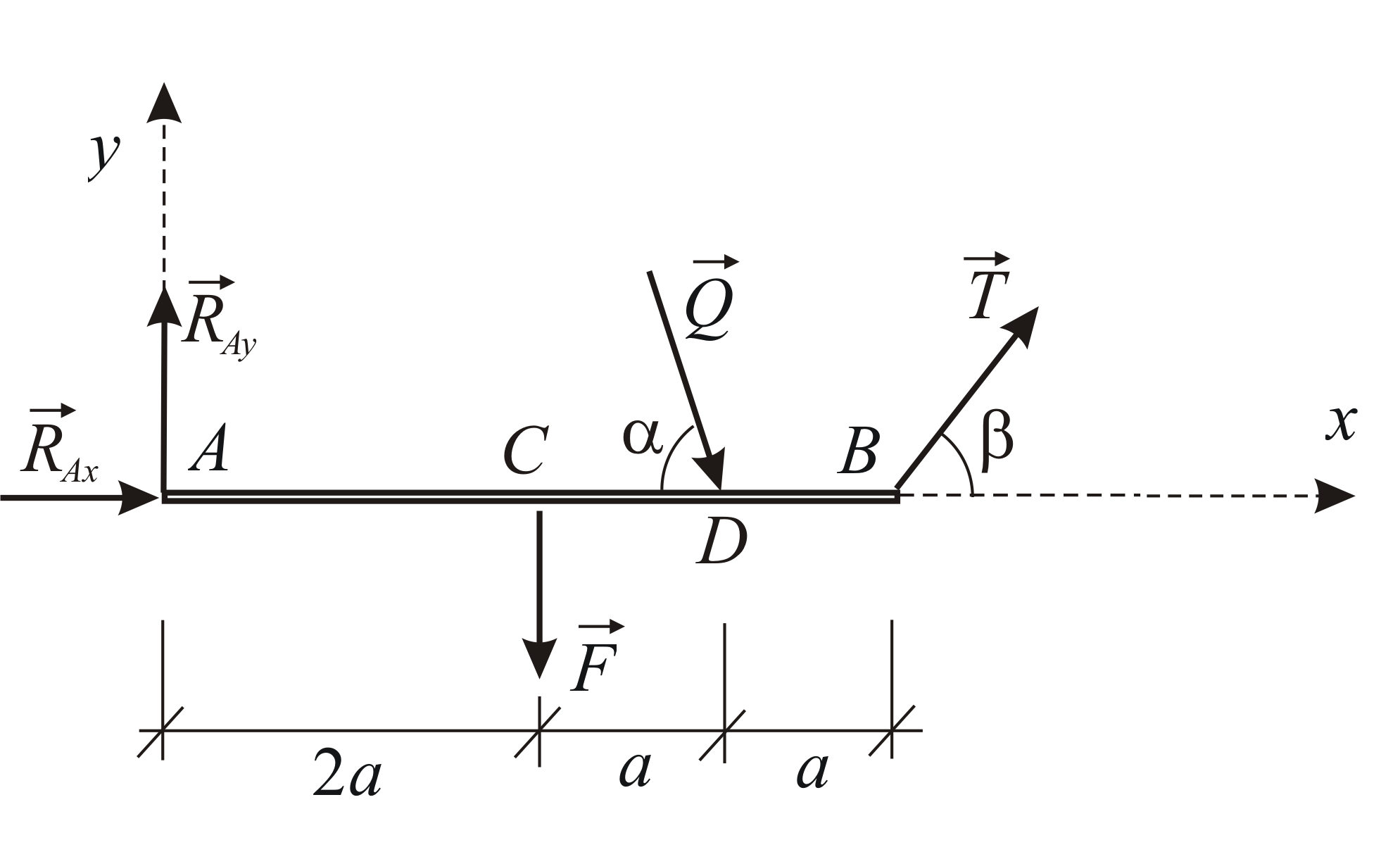
Рис. 1.15		Рис. 1.16

Неизвестную по модулю и направлению силу представим двумя неизвестными по модулю составляющими, направленными вдоль выбранных координатных осей. Направление реакции в точкеизвестно. Заданную силуимеет смысл разложить в точкена две составляющие, параллельные координатным осям. Силовая схема представлена на Рис.1.16.

Условия равновесия в рассматриваемом случае имеют вид:

Решая полученную систему уравнений, находим:

Остаётся определить силу тяжести противовеса.

Рассмотрим равновесие тела (Рис.1.17). Получаем:

Рассмотрим равновесие блока (Рис.1.18). Составляя уравнение моментов относительно оси блока, получаем:

Таким образом,

Рис. 1.17		Рис. 1.18

Как видно, натяжения концов нити, переброшенной через блок, при отсутствии трения одинаковые.

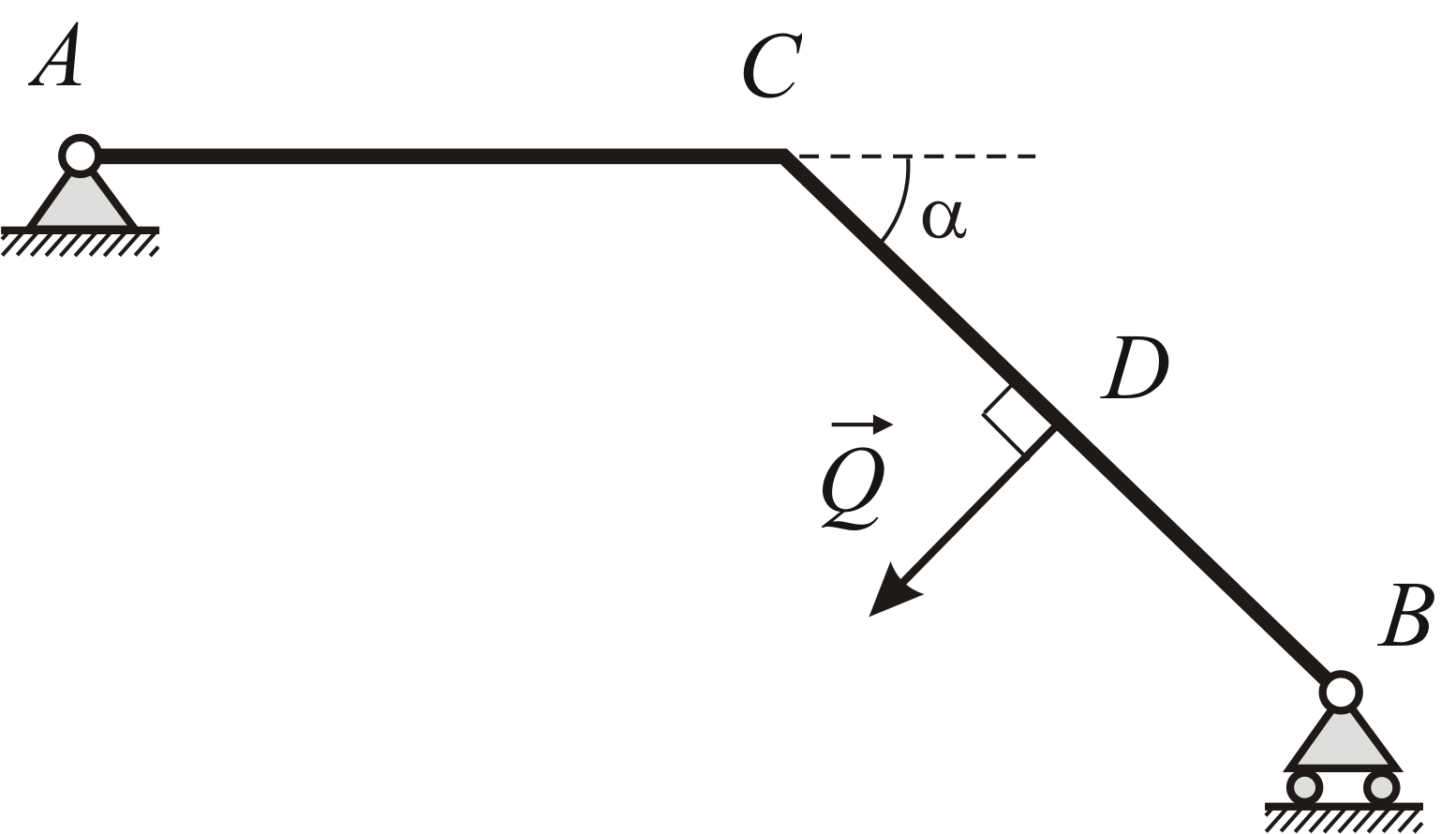
Пример 1.2

Ломаный стержень имеет шарнирно неподвижную опору в точкеи шарнирно подвижную опору в точке. В точкеприложена сила, линия действия которой перпендикулярна(Рис.1.19). Дано:кН,м,м,Определить реакции опор.

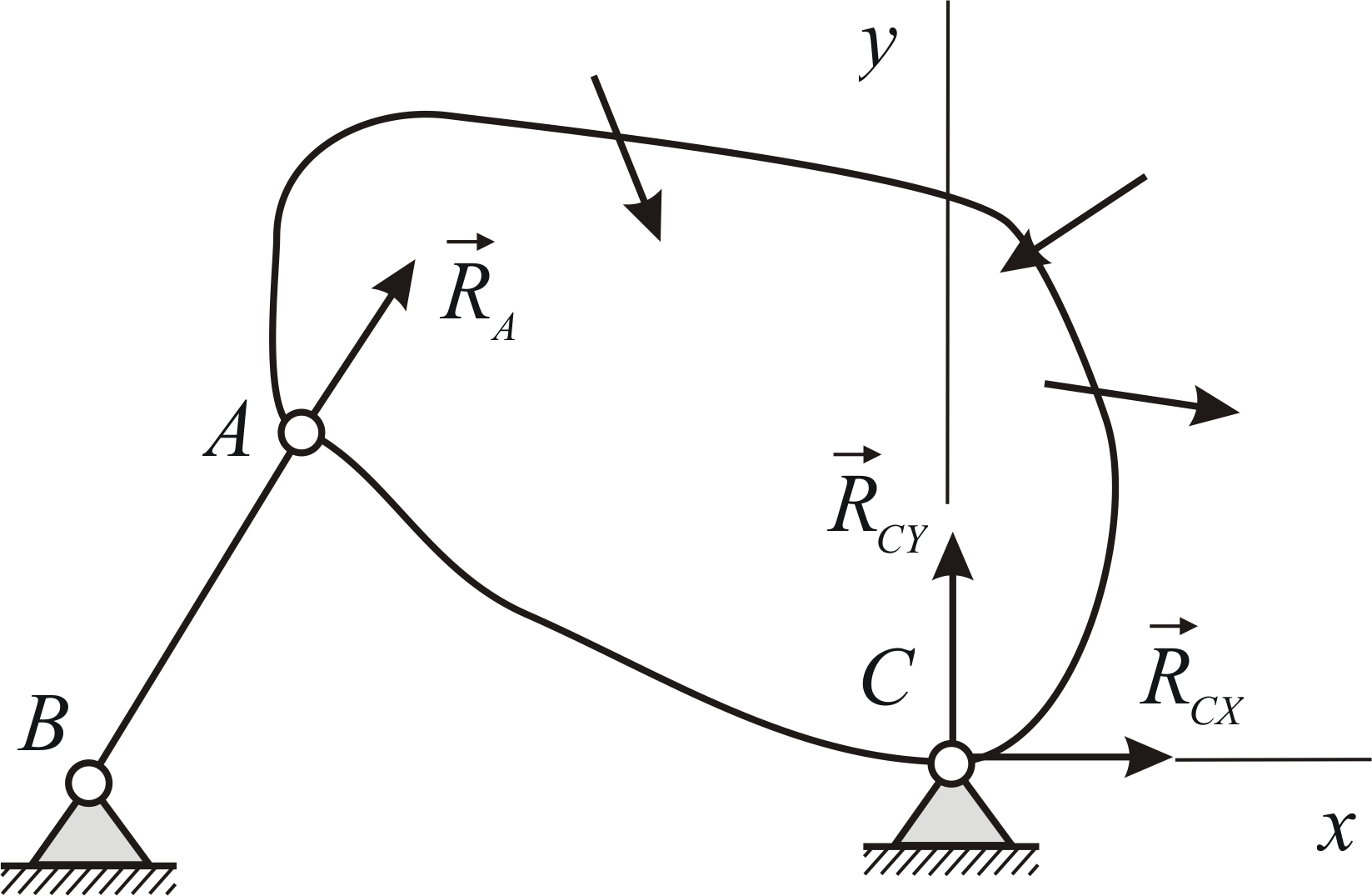
Рассмотрим равновесие стержня . Направление реакции шарниразаранее неизвестно. Можно определить линию действия этой силы при помощи теоремы о трёх силах и решить задачу графически. Однако на таком пути часто возникают хотя и преодолимые, но неоправданные сложности, связанные с решением чисто геометрических проблем. Намного эффективнее аналитический путь решения задачи.

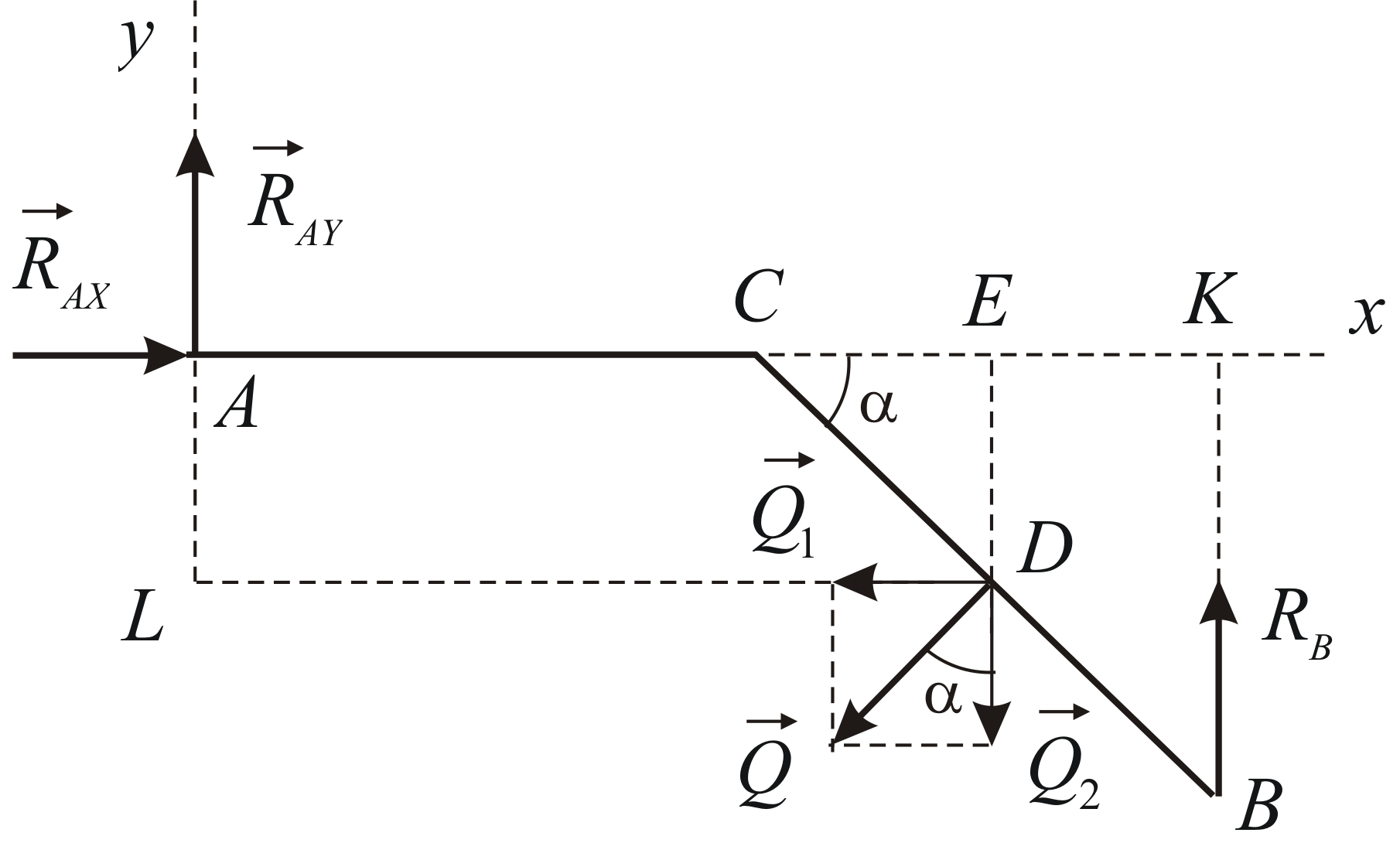
Рис. 1.19		Рис. 1.20

Неизвестную по модулю и направлению силу представим двумя неизвестными по модулю составляющими, направленными вдоль выбранных координатных осей. Направление реакции в точкеизвестно. Заданную силуимеет смысл разложить в точкена две составляющие, параллельные координатным осям. Силовая схема представлена на Рис.1.20.

Условия равновесия в рассматриваемом случае имеют вид:

Решая полученную систему уравнений, находим:

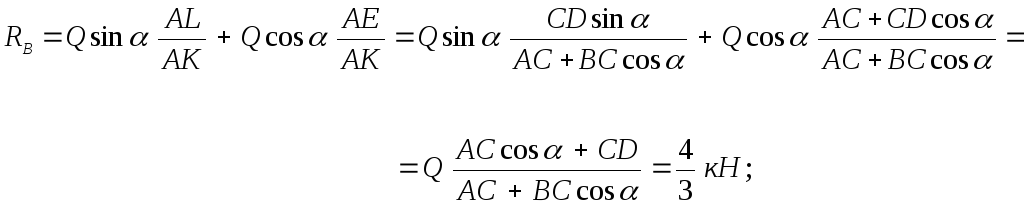
Замечание.

Имеет смысл получать решение в общем виде (в буквенных обозначениях). Численные значения следует подставлять только на последнем этапе решения задачи.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:

1. Какова методика решения задач об определении реакций опор?

2. Каковы условия равновесия плоской системы сил?

3. Как вычисляется проекция вектора силы на координатную ось?

4. Как вычисляется момент силы относительно оси, перпендикулярной плоскости расположения сил?

5. Как представляется реакция шарнирно-подвижной и шарнирно-неподвижной опор?

6. Как представляется реакция троса, гладкой поверхности и стержневой опоры?

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 2.28; 2.29; 2.30; 2.31; 2.41; 4.7; 4.8; 4.10; 4.11; 4.12; 4.13; 4.14; 4.15.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплект СР-1.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2