4.2. Теорема об изменении кинетического момента относительно неподвижной оси

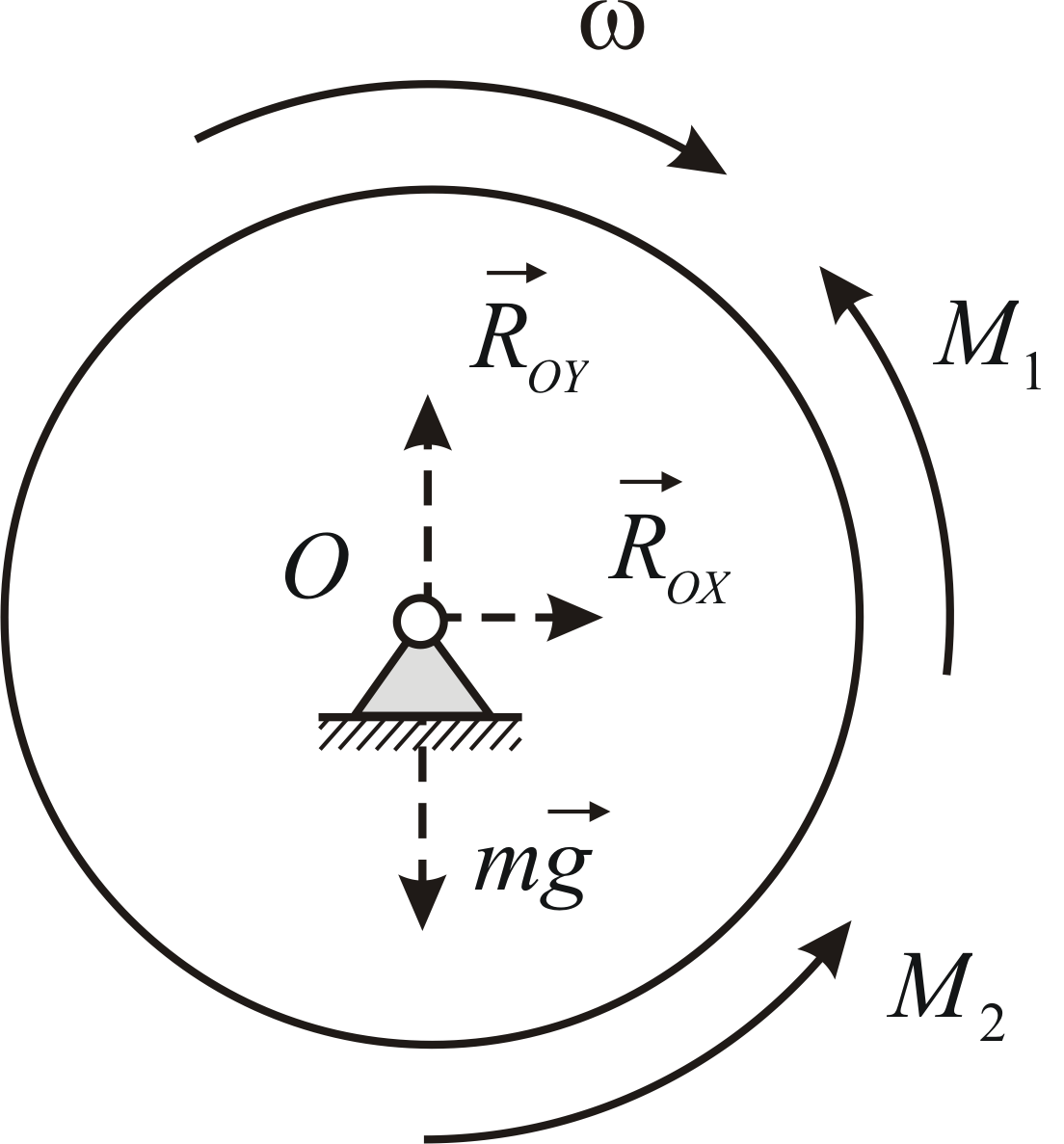
Пример 4.7

Маховик вращается вокруг оси, проходящей через его центр масс, с угловой скоростью . Электрический тормоз создает тормозящий момент, пропорциональный угловой скорости маховика. Моментот трения в подшипниках считается постоянным (Рис.4.7). Определить, через какой промежуток времениостановится маховик, если момент инерции маховика относительно оси вращения.

Рис.4.7

Дифференциальное уравнение вращательного движения в рассматриваемом случае имеет вид:

или

Интегрируя полученное уравнение при заданных начальных условиях:

определяем время торможения:

.

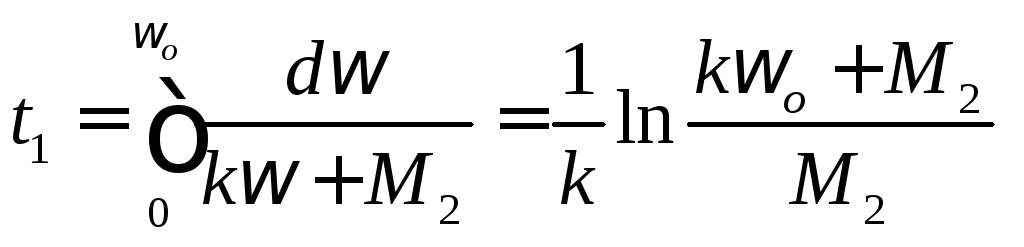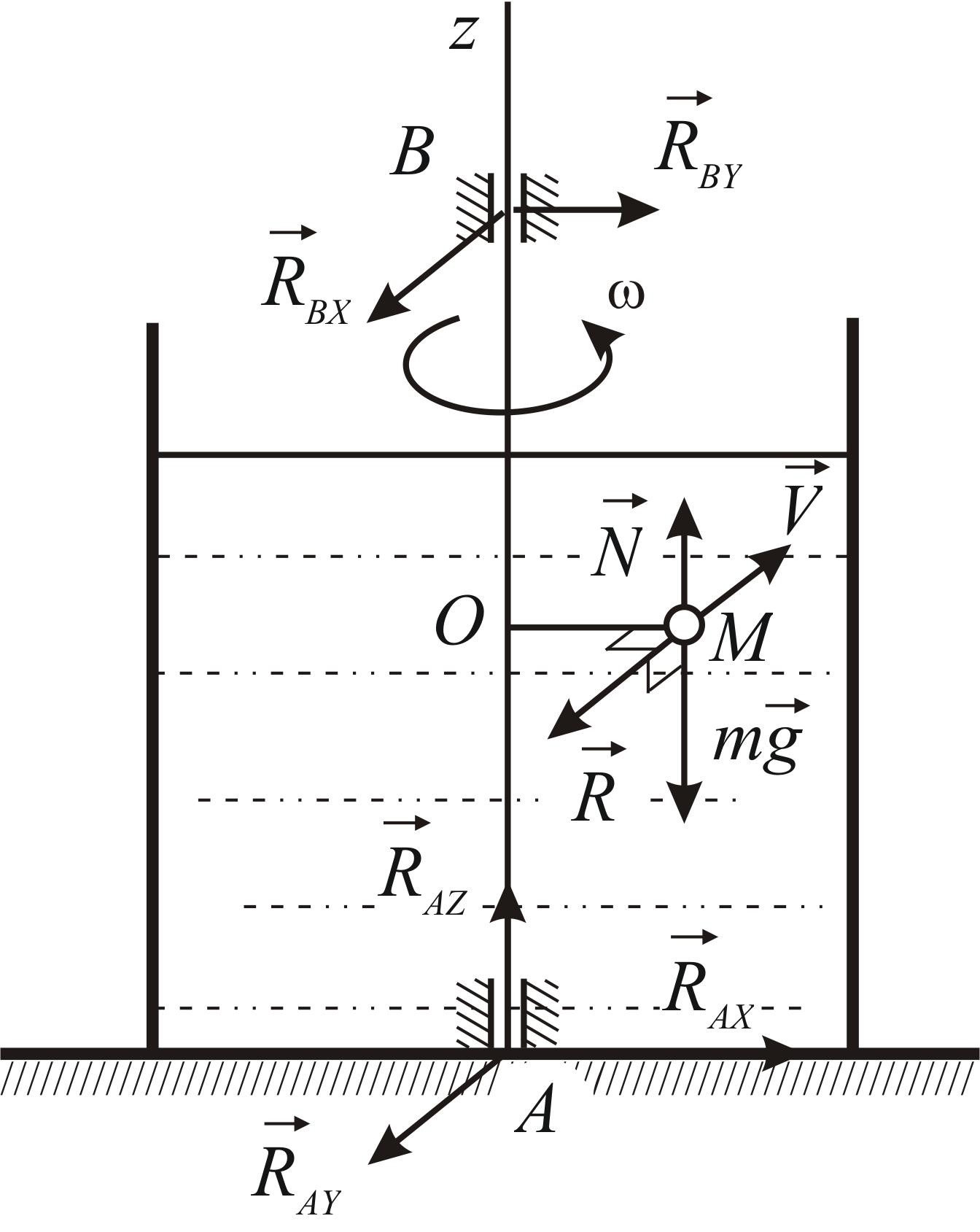
Пример 4.8

Шарик , находящийся в сосуде с жидкостью и прикрепленный к концу стержнядлины, приводится во вращение вокруг вертикальной осис начальной

угловой скоростью (Рис. 4.8). Сила сопротивления жидкости пропорциональна угловой скорости. Определить, через какой промежуток времениугловая скорость стержня станет в два раза меньше начальной, а также число оборотов, которое сделает стержень за этот промежуток времени. Массу шарика считать сосредоточенной в его центре, массой стержня пренебречь.

В динамике, также как и в статике, существенное значение имеет правильный выбор тела, движение которого будет рассматриваться. В данной задаче имеет смысл рассмотреть движение системы, состоящей из шарика и стержней и. При таком выборе неизвестные реакции опор не войдут в уравнение движения. На Рис. 4.8 изображены все внешние силы, действующие на указанную систему. Из всех этих сил только одна – сила сопротивления создает момент относительно оси вращения системы:

или

Поскольку формулировка задачи содержит несколько вопросов, имеет смысл интегрировать уравнение с переменным верхним пределом:

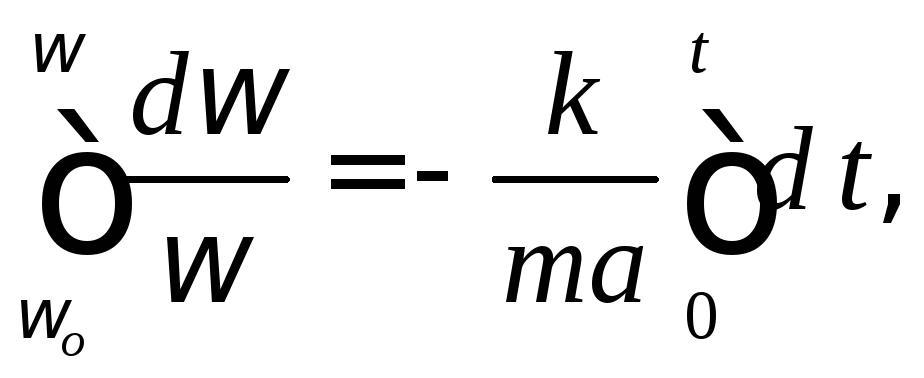откуда и

Рис.4.8

Полагая в полученном решении, определяем промежуток времени, по истечение которого угловая скорость уменьшится наполовину:

Число оборотов , сделанных стержнем за время, связано с углом поворота стержня:. Интегрируя равенство, получаем:

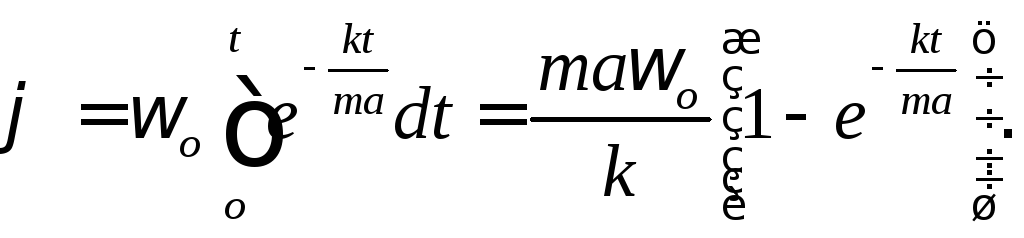
Подставляя сюда значение , получаем:

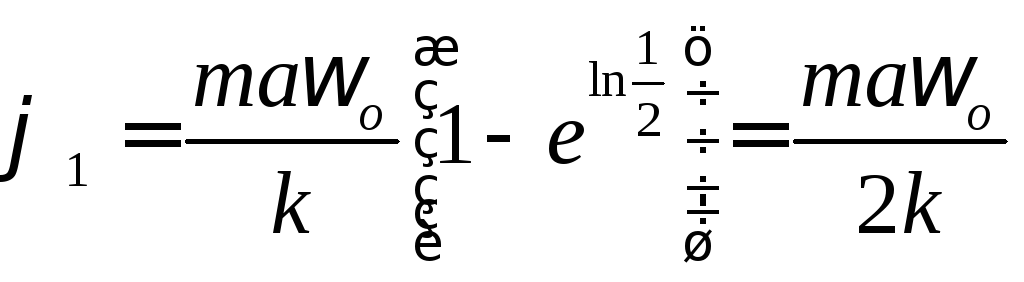и, следовательно, Вращение механической системы с изменяющимся осевым моментом инерции

Если в процессе движения момент инерции системы относительно оси вращения изменяется, используется теорема об изменении момента количества движения механической системы относительно неподвижной оси:

.

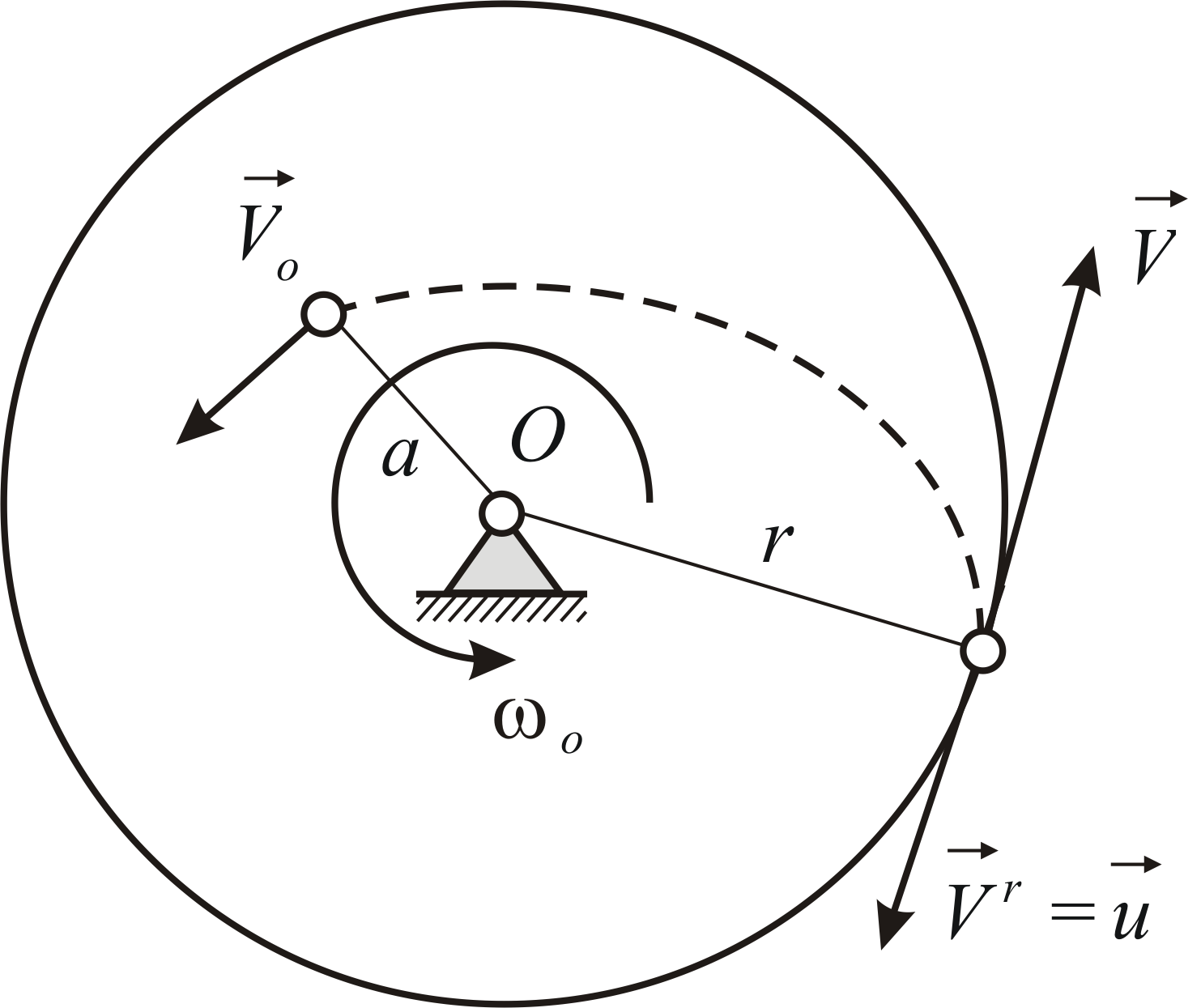
Пример 4.9

Круглая горизонтальная платформа вращается без сопротивления вокруг вертикальной оси с угловой скоростью . При этом на расстоянииот оси вращения стоит человек, масса которого равна(Рис.4.9). Момент инерции платформы относительно оси вращения равен, радиус –. Как изменится угловая скорость платформы, если человек перейдет на ее край и начнет двигаться по ее ободу против вращения с относительной скоростью?

Рис. 4.9

Приложенные к системе внешние силы (силы тяжести и реакции шарнира) не создают момента относительно оси вращения, следовательно, имеем закон сохранения кинетического момента относительно оси:

Отсюда:

где – скорости, сообщаемые человеку платформой. Окончательно получаем:

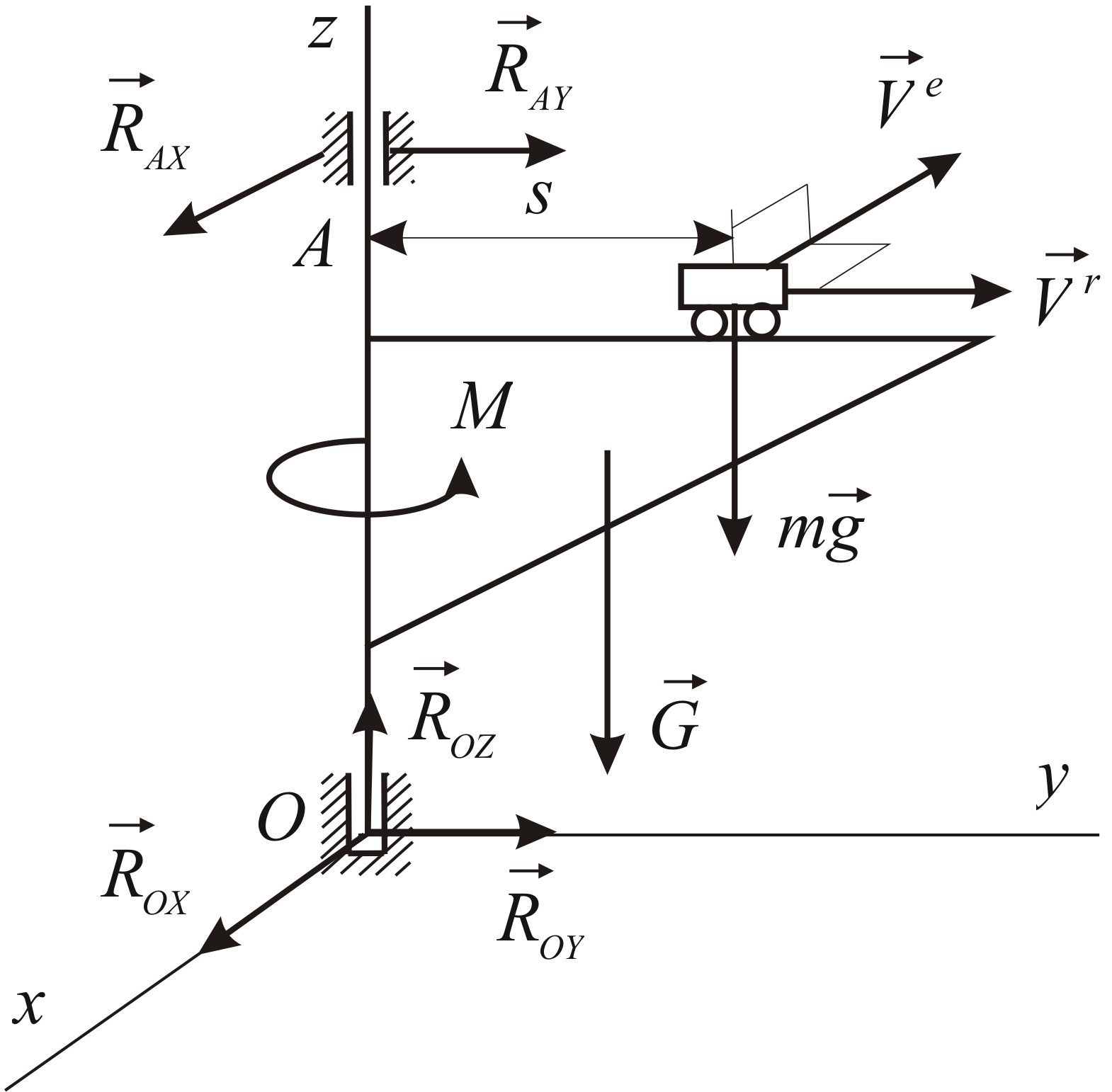
Пример 4.10

Тележка поворотного подъемного крана движется с постоянной относительной скоростью относительно стрелы (Рис. 4.10). Мотор, вращающий кран, создает в период разгона постоянный вращающий момент. Определить угловую скорость крана в зависимости от расстоянияот тележки до оси вращения, если масса тележки с грузом равна; момент инерции крана без тележки относительно оси вращения равен. Вращение начинается в момент, когда тележка находится на расстоянииот оси крана.

Теорема об изменении кинетического момента относительно оси в рассматриваемом случае приводит к уравнению:

интегрируя которое при нулевых начальных условиях, получаем:

Рис. 4.10

Кинетический момент системы относительно оси вращения складывается из кинетического момента крана без тележки и кинетического момента тележки. Количество движения тележки можно разложить на две составляющие – относительную, которую получает тележка при своем движении по стреле крана, и переносную, которую сообщает тележке кран при повороте стрелы. Момент относительно оси вращения крана создает только переносная составляющая количества движения тележки.

Таким образом,

где – скорость той точки стрелы, в которой находится тележка. Окончательно получаем:

Следовательно,

Относительное движение тележки равномерное:

Отсюда: