1. Первая и вторая задачи динамики материальной точки

Пример 1.1

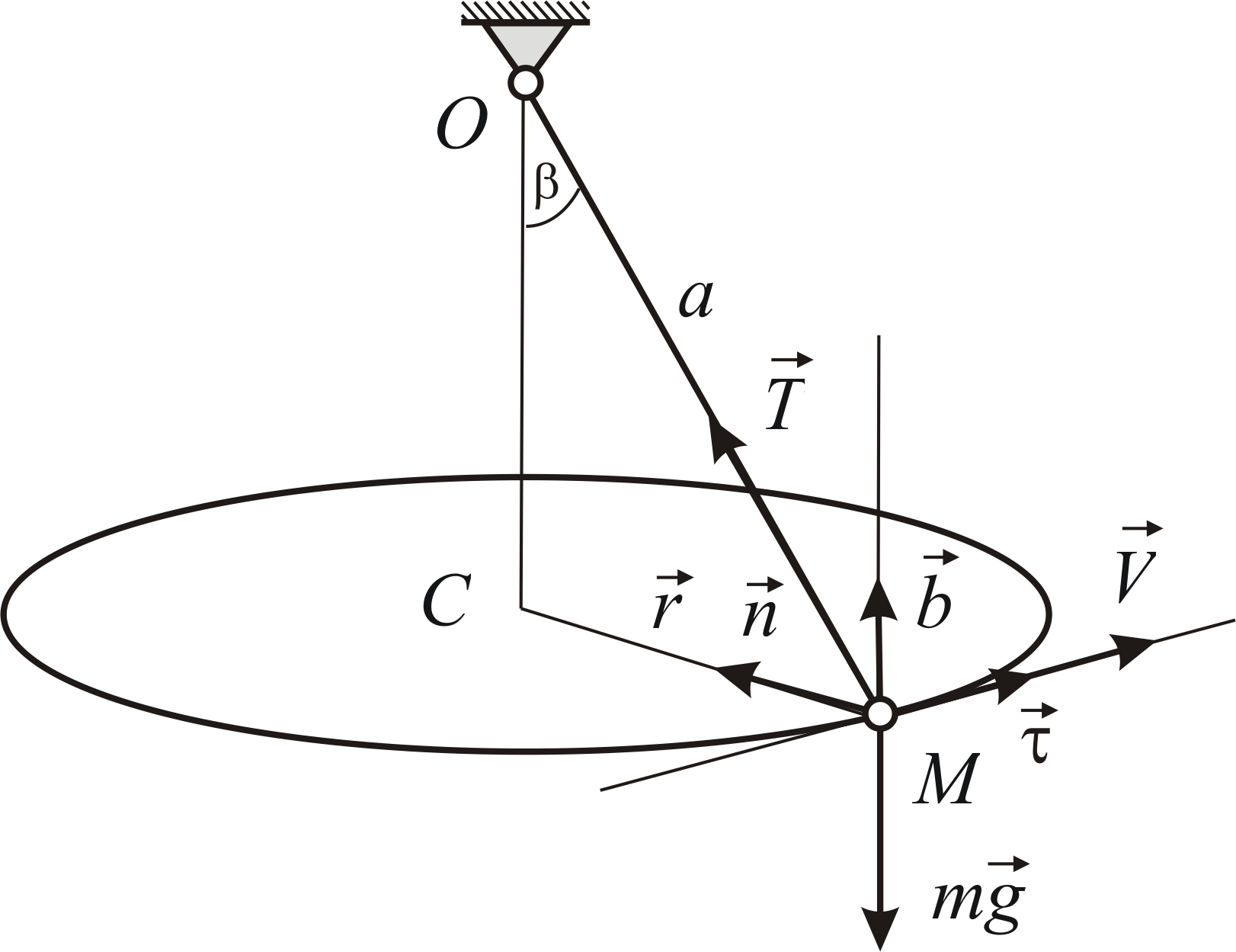
Груз массы, подвешенный на нити длины, другой конец которой закреплен в точке, представляет собой конический маятник, т.е. описывает окружность в горизонтальной плоскости (Рис.1.1). Нить образует с вертикалью угол. Определить скорость грузаи силу натяжения нити.

Рис.1.1

Рассмотрим движение груза, который по условию задачи можно считать материальной точкой. Поскольку траектория точки известна, используем уравнения движения в проекциях на оси естественного трёхгранника. В рассматриваемом случае эти уравнения имеют вид:

Последнее уравнение позволяет определить силу :Из первого уравнения можно сделать вывод, что в процессе движения скорость точки не изменяет свою величину; определить эту величину можно из второго уравнения:

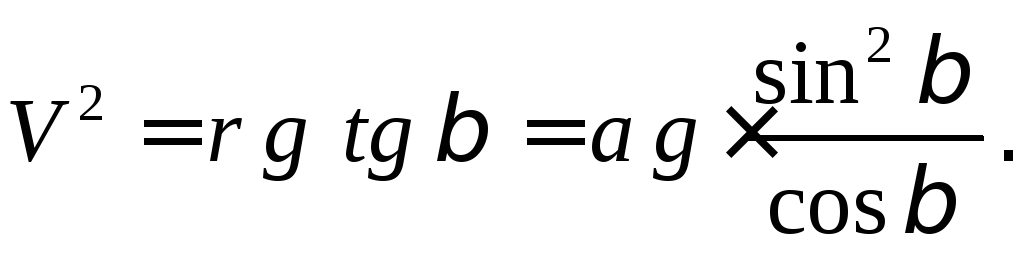
Заметим, что в решении фигурирует сила реакции нити, но искомая сила натяжения нити равна ей по модулю.

Пример 1.2

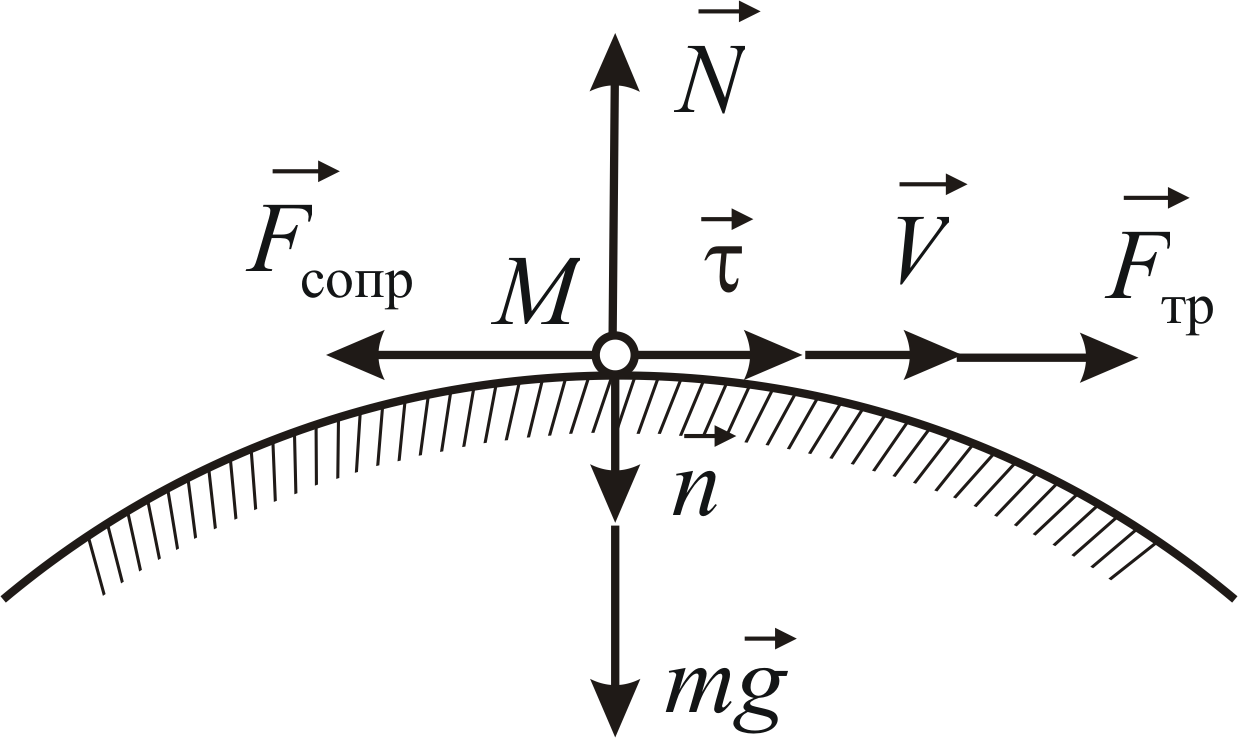
Автомобиль массы движется по выпуклому мосту равномерно со скоростью(Рис.1.2). Радиус кривизны в середине моста. Определить силу давления автомобиля на мост в момент прохождения его через середину моста.

Рис.1.2

Рассмотрим автомобиль в верней точке моста. Силы, действующие в направлении касательной к траектории – сила трения, сила сопротивления воздуха неизвестны. В направлении главной нормали к траектории действуют известная сила тяжести и нормальная реакция опоры, которую и требуется определить. Поэтому запишем уравнение движения в проекциях на главную нормаль к траектории. В рассматриваемом случае это уравнение принимает вид:

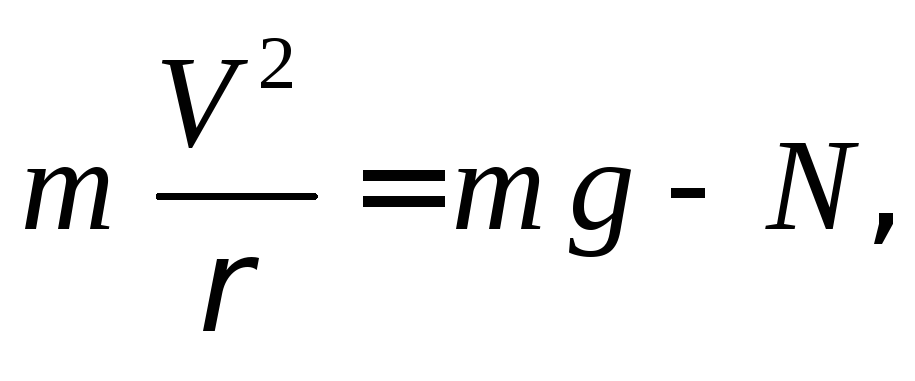отсюда:

По третьему закону Ньютона сила давления автомобиля на мост по модулю равна нормальной реакции.

Пример 1.3

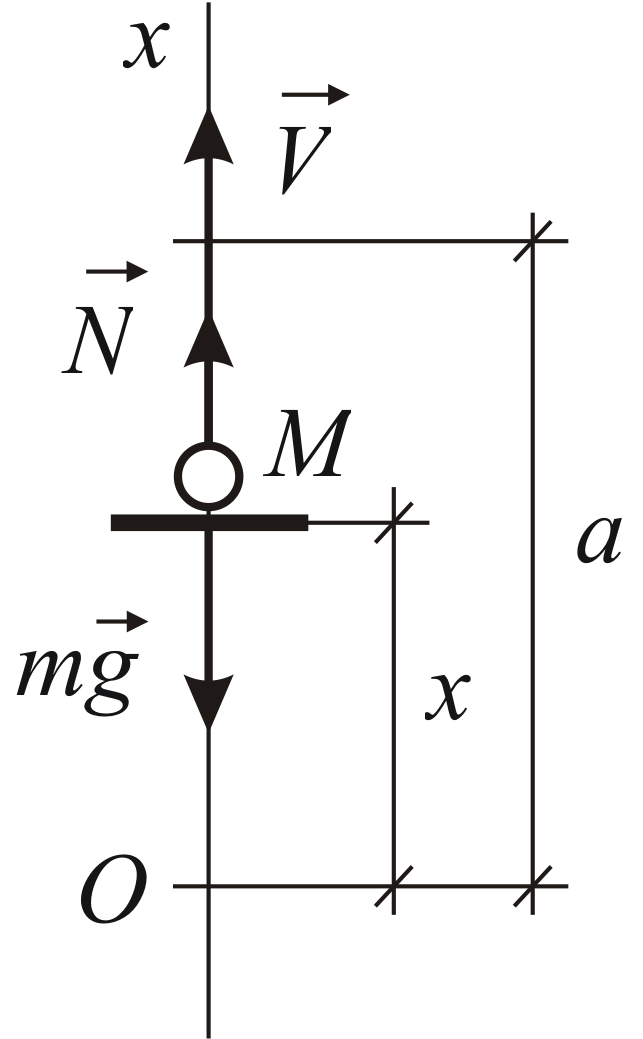
Решето рудообогатительного грохота движется поступательно по вертикали по закону . Найти наименьшую частотуколебаний решета, при которой куски руды, лежащие на нем, будут отделяться от него и подбрасываться вверх.

Рис.1.3.

Направим осьвертикально вверх (Рис.1.3). Дифференциальное уравнение движения имеет вид:

Отсюда:

Минимальное значение нормальная реакция принимает в верхней точке, где :

Если кусок руды отделяется от решета, то отсюда

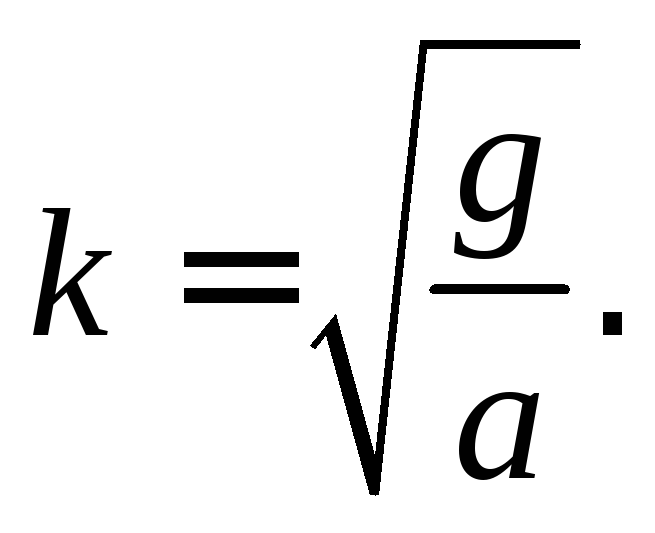
Пример 1.4

Материальная точка массы совершает прямолинейное движение под действием силы, изменяющейся по закону, гдеи— постоянные величины. В начальный момент точка имела скорость. Найти уравнение движения точки.

Направим ось вдоль прямой, по которой движется точка, совместив начало отсчета с начальным положением точки. На основании второго закона Ньютона в проекции на осьполучаем:

Интегрируя полученное дифференциальное уравнение движения точки

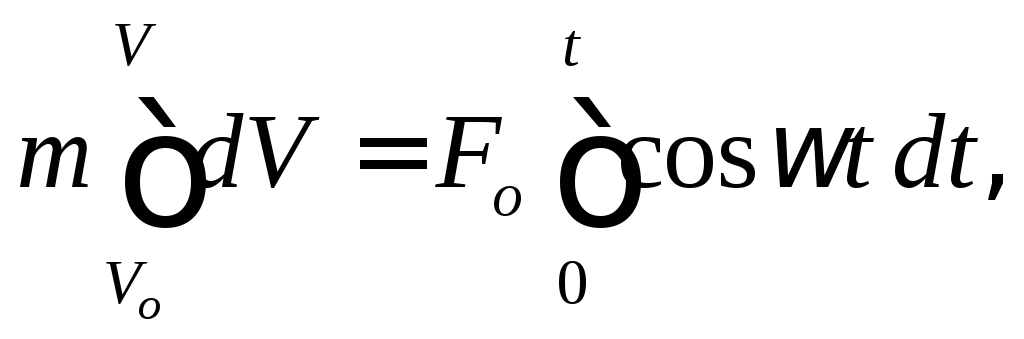
определяем зависимость ее скорости от времени:

Поскольку , полученное уравнение представляет собой дифференциальное уравнение относительно функции:

интегрируя которое, определяем закон движения точки:

Пример 1.5

На какую высоту и за какое времяподнимется тело весом, брошенное вертикально вверх со скоростью, если сопротивление воздуха может быть выражено формулой, где— скорость тела?

Направим ось вертикально вверх, полагаяна поверхности Земли (Рис.1.4). Дифференциальное уравнение движения имеет вид:

или, учитывая что , вид:

Рис.1.4

Уравнениепредставляет собой обыкновенное дифференциальное уравнение первого порядка с разделяющимися переменными. Чтобы получить зависимость скорости от времени, выполняем интегрирование с переменным верхним пределом. Учитывая начальные условия, получаем:

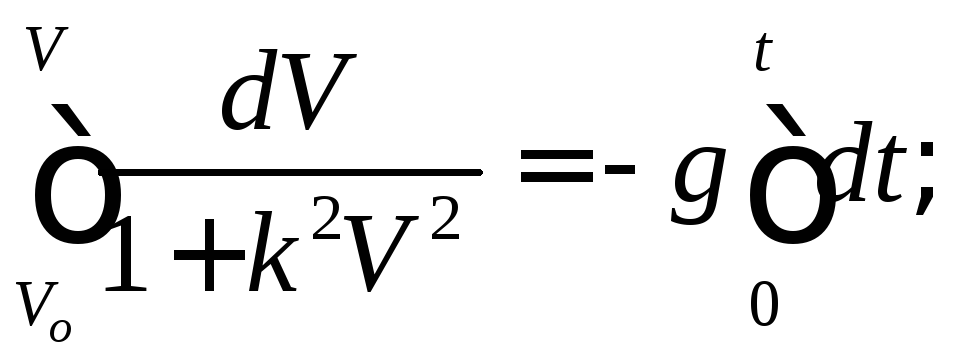
отсюда:

Теперь мы имеем возможность определить время подъема тела на максимальную высоту. Подставляя в уравнение (с) условия

при получаем

Остается определить максимальную высоту подъема . Уравнениеможно рассматривать как дифференциальное уравнение относительно функции, поскольку, но интегрирование уравнения

представляется неудобным.

Помимо зависимости , для определениянас вполне устраивает зависимость, поскольку скорость в верхней точке известна:. Перейдем в уравненииот производной пок производной по, полагая

Уравнение принимает вид:

Интегрируя уравнение

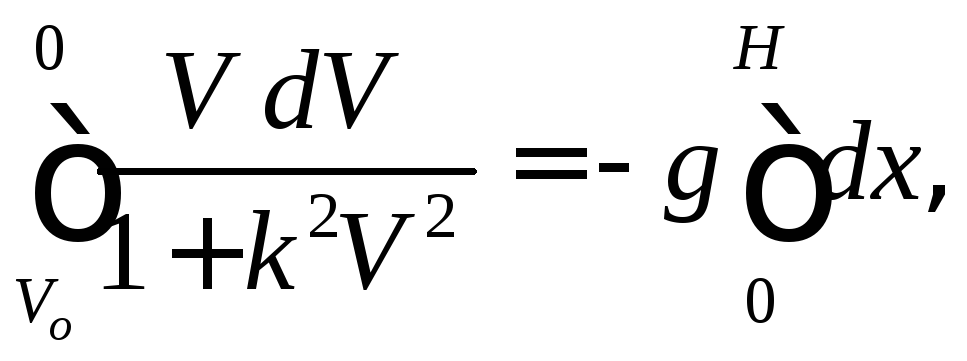получаем:

Заметим, что соотношение представляет собой одну из форм записи теоремы об изменении кинетической энергии, которую мы докажем позднее.