
Лекция 7
.docЛЕКЦИЯ 7.
1. О приведении общего уравнения 2-го порядка на плоскости к каноническому виду
Напомним, что это уравнение имеет вид
![]() ,
(1)
,
(1)
где
![]() .
(2)
.
(2)
Функция двух переменных
![]()
называется квадратичной формой, а матрица
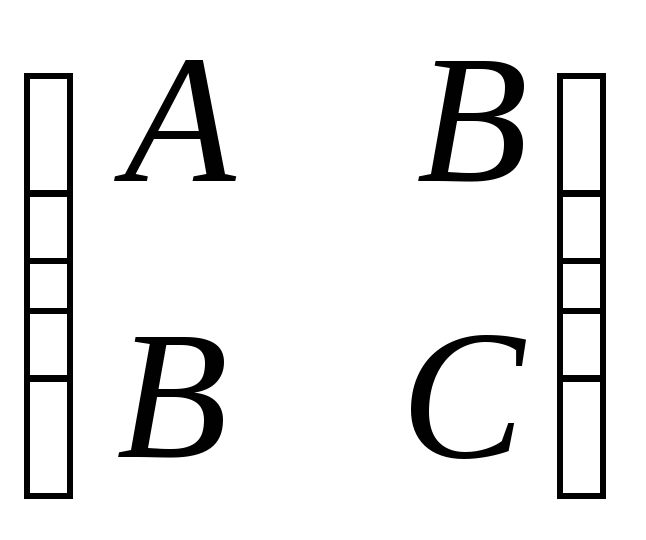
называется матрицей квадратичной формы. (Она симметрична, т.е. совпадают коэффициенты, симметрично расположенные относительно главной диагонали).
Ее коэффициенты A и С, стоящие на главной диагонали – это коэффициенты при «квадратах»: при x2 и y2 соответственно.
Смешанный член 2Bxy можно записать так
![]() ,
,
так что B есть коэффициент как при xy, так и при yx, поэтому он занимает 2 места на побочной диагонали.
Определитель этой матрицы есть величина
![]() .
.
Оказывается, знак этого определителя, а также знаки коэффициентов A и С при квадратах играют решающую роль при выяснении вопроса о типе кривой, заданной общим уравнением (1).
Функция двух переменных
![]()
есть, по определению, линейная функция.
Таким образом, левая часть уравнения (1) есть сумма:
квадратичная форма + линейная функция.
Все вместе есть квадратичная функция, или многочлен второй степени от переменных x и y.
Какие кривые или линии на плоскости может определять алгебраическое уравнение второго порядка (1) с условием (2)? Во-первых, общее уравнение (1) с условием (2) может определять одну из 3-х рассмотренных нами кривых второго порядка: эллипс, гиперболу или параболу (из которых первые две являются центральными, а последняя центра не имеет). Если это так, то параллельным сдвигом и поворотом координатных осей можно привести (1) к каноническому виду одной из трех указанных кривых.
Пример. Если
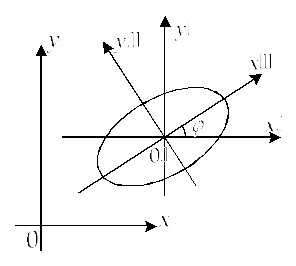
уравнение (1) задает произвольный эллипс,
то сдвиг начала координат в точку
![]() и поворот на угол
приводят уравнение эллипса к каноническому
виду
и поворот на угол
приводят уравнение эллипса к каноническому
виду
![]()
Кроме того, (1) может определять пару прямых:
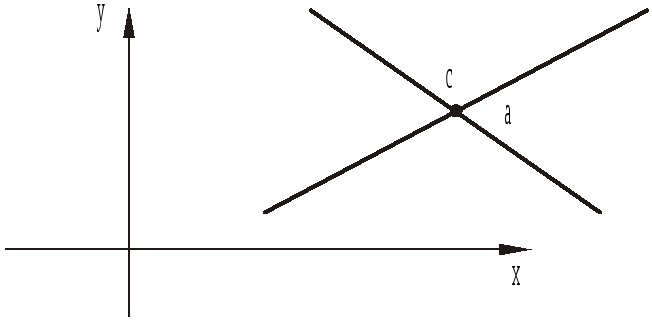
а) пересекающихся, например:
![]() или
или
![]() ,
,
и в этом случае у множества решений уравнения (1), т.е. у пары прямых, есть центр симметрии – точка пересечения прямых;
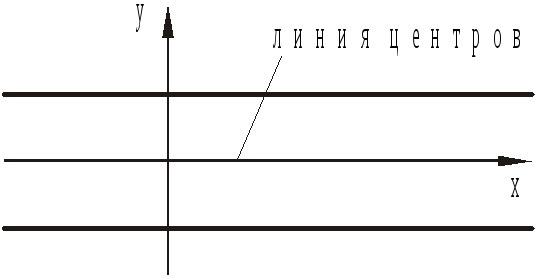
б) параллельных, например:
![]() или
или
![]()
и в этом случае есть линия центров симметрии,
а, значит, снова по крайней мере один центр есть;
в) совпадающих, например:
![]() .
.
Снова есть линия центров, совпадающая с прямой.
Далее, (1) может определять точку, например
![]()
– «вырожденный» эллипс.
В этом случае опять центр есть.
Наконец, (1) может определять пустое множество
![]() .
.
Определитель матрицы квадратичной формы
![]()
не меняется при сдвиге и повороте, или говорят, что он является инвариантом этих преобразований. В связи с этим линии второго порядка классифицируются по следующим трем типам:
1) эллиптический,
при
![]() ;
;
2) гиперболический,
при
![]() ;
;
3) параболический,
при
![]() .
.
Такую же классификацию мы будем применять к уравнению (1).
Теорема. В зависимости от типа общее уравнение второго порядка
![]()
определяет одну из следующих линий:
-
эллиптический тип: эллипс, точка, пустое множество;
-
гиперболический тип: гипербола, пара пересекающихся прямых;
-
параболический тип: парабола, пара параллельных прямых, пара совпадающих прямых.
Доказывается, что для того, чтобы линия оказалась эллипсом необходимо, чтобы уравнение имело эллиптический тип, гиперболой – гиперболический, параболой – параболический.
Однако это лишь
необходимые условия, но не достаточные.
Например, уравнение эллиптического
типа может определять и точку
![]() – вырожденный эллипс, и пустое множество
– вырожденный эллипс, и пустое множество
![]() .
.
2. Решение задач по теме "Кривые второго порядка на плоскости"
Задача 1.
Найти точки пересечения прямой
![]() и эллипса
и эллипса
![]() .
.
Решение. Точки пересечения лежат одновременно на прямой и на эллипсе их координаты удовлетворяют одновременно обоим уравнениям надо решить систему
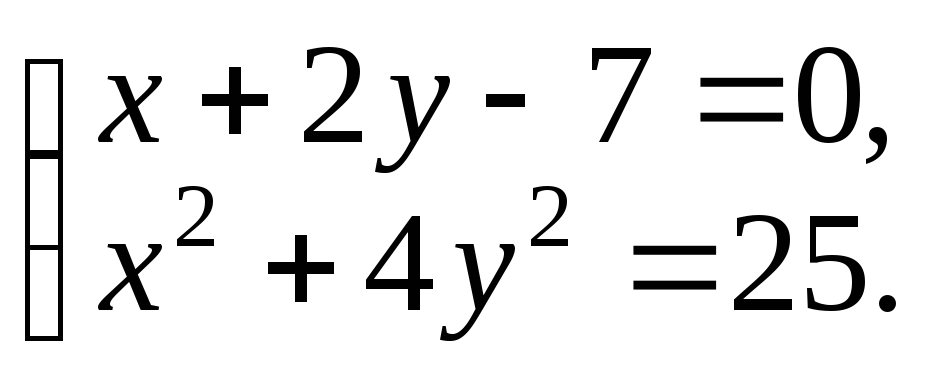
Выражаем x
из первого
уравнения:
![]() и подставляем во второе:
и подставляем во второе:
![]() .
Решаем:
.
Решаем:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
![]() .
.
Подставляем
найденные значения в первое уравнение
и находим соответствующие x:
![]() ;
;
![]() .
.
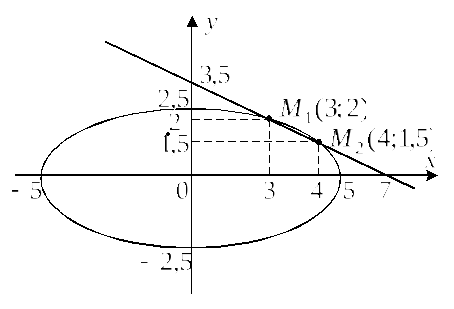
Ответ:
![]() ,
,
![]() .
.
Задача 2. Установить, какая линия определяется уравнением
![]()
и нарисовать ее на плоскости в системе координат.
Решение. Преобразуем уравнение:
![]() ;
;
![]() ;
;
выделяем полный
квадрат
![]() ;
;
![]() ;
;
раскрываем скобки:
(-4):
![]() .
.
Делим на (-4) и получаем каноническое уравнение гиперболы:
![]()
с центром в точке
(2; -1) и полуосями
![]() .
.
Но исходное уравнение задает не всю гиперболу, а только ее часть. При возведении в квадрат надо учесть, что обе части равенства должны быть одного знака, т.е.
![]() .
.
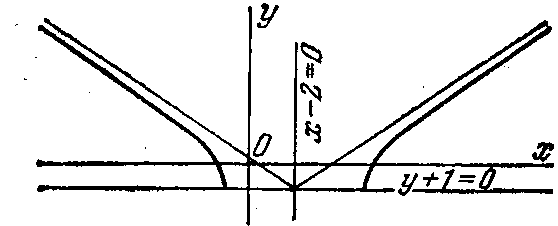
Получается часть
гиперболы, расположенная над прямой
![]() .
.
3. Общее уравнение поверхности второго порядка
Рассмотрим общее уравнение второй степени в пространстве
![]() . (3)
. (3)
Это уравнение
связывает три пространственные переменные
![]() и определяет поверхность
второго порядка. Классификация
поверхностей второго порядка в
пространстве сложнее и разнообразнее,
чем классификация кривых 2-го порядка
на плоскости.
и определяет поверхность
второго порядка. Классификация
поверхностей второго порядка в
пространстве сложнее и разнообразнее,
чем классификация кривых 2-го порядка
на плоскости.
Уравнение (3) может определять поверхность в обычном смысле, но могут возникнуть и вырожденные случаи, например, пара плоскостей (пересекающихся, параллельных, совпадающих) или точка, или пустое множество.
Мы обратимся сейчас к некоторым важным поверхностям, представленным в канонической форме.
4. Эллипсоид
Уравнение
![]()
называется каноническим уравнением эллипсоида.
Эллипсоид – поверхность, которая в некоторой системе координат может быть представлена этим уравнением.
Здесь
![]() – полуоси эллипсоида. Положим
– полуоси эллипсоида. Положим
![]() .
Получим сечение эллипсоида координатной
плоскостью XOY
– эллипс:
.
Получим сечение эллипсоида координатной
плоскостью XOY
– эллипс:
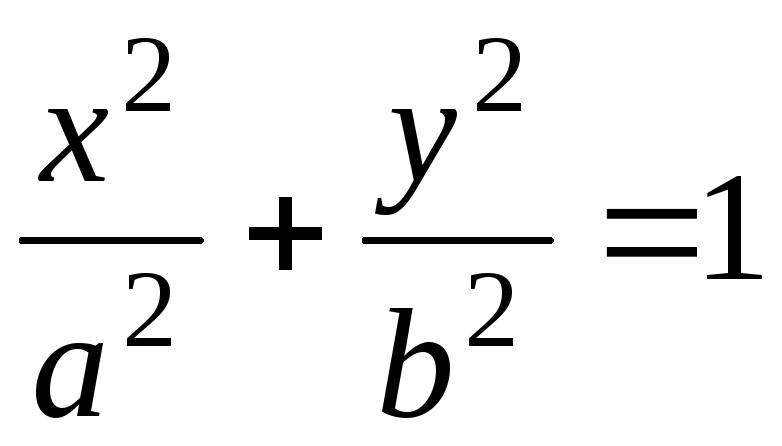
Сечения другими координатными плоскостями также представляют собой эллипсы.

Если
![]() ,
то эллипсоид превращается в шар радиуса
R
с центром в начале координат:
,
то эллипсоид превращается в шар радиуса
R
с центром в начале координат:
![]() .
.
5. Другие канонические поверхности второго порядка
Задание. Рассмотрите и нарисуйте поверхности (см. Клетеник "Сборник задач ..." §46):
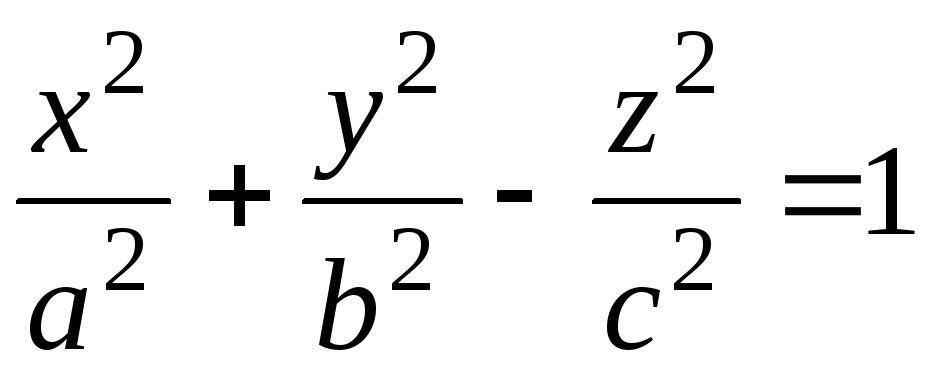 –
однополостный гиперболоид,
–
однополостный гиперболоид,
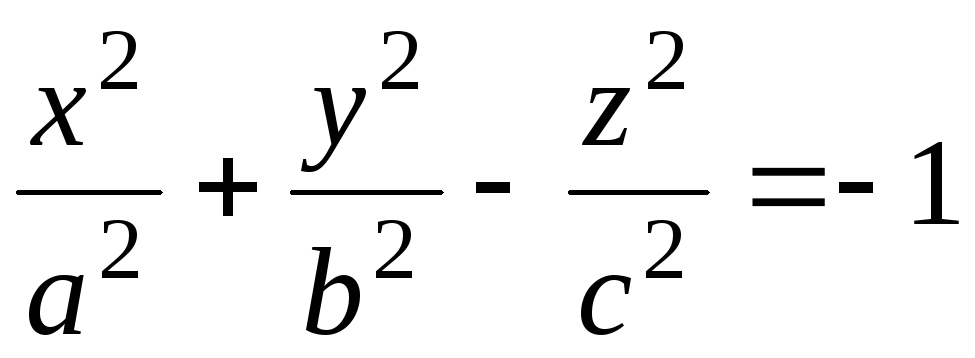 – двуполостный
гиперболоид,
– двуполостный
гиперболоид,
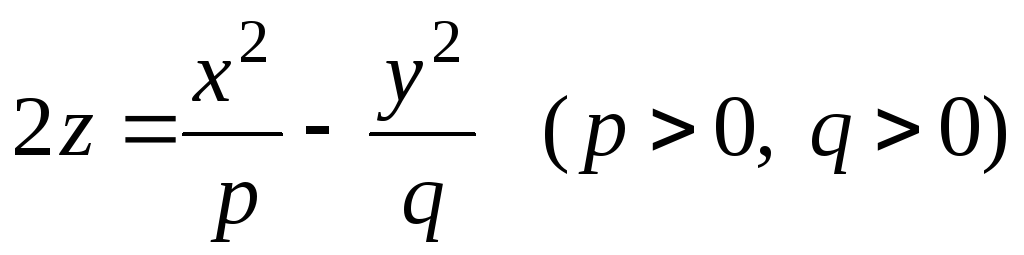 –
гиперболический
параболоид (седло),
–
гиперболический
параболоид (седло),
![]() –
эллиптический параболоид,
–
эллиптический параболоид,
 –
коническая
поверхность,
–
коническая
поверхность,
![]() – цилиндрическая
поверхность.
– цилиндрическая
поверхность.
Первая поверхность – однополостный гиперболоид получается при вращении прямой вокруг оси, которая с ней скрещивается (то есть не параллельна и не пересекается).

На этой идее основана сетчатая конструкция башни, созданная из стальных балок архитектором Шуховым в 1920-22 гг. Это знаменитая Радио- и Теле- башня на Шаболовке в Москве.


