Лекция 14

ЛЕКЦИЯ 14. ЗНАКООПРЕДЕЛЕННЫЕ КВАДРАТИЧНЫЕ ФОРМЫ. КРИТЕРИЙ СИЛЬВЕСТРА

1. Знакоопределенность квадратичных форм.

Пусть

– симметричная матрица порядка n, Q(x) = (Ax, x) – соответствующая квадратичная форма, где .

Квадратичная форма Q(x) называется положительно определенной, если

для всех .

Квадратичная форма Q(x) называется неотрицательно определенной, если

и такой, что .

Квадратичная форма называется отрицательно определенной, если

.

Квадратичная форма называется неположительно определенной, если

и такой, что .

Ясно, что

Q(x) – отрицательно определенная положительно определенная,

Q(x) – неположительно определенная неотрицательно определенная.

Поэтому мы будем рассматривать только условия положительной и неотрицательной определенностей.

Квадратичная форма называется знакоопределенной, если она является положительно, неотрицательно, отрицательно или неположительно определенной.

Примеры.

1⁰. – положительно определенная в R².

2⁰. – неотрицательно определенная, но положительно определенной не является, так как Q(x) = 0 на прямой x₁ = – x₂.

3⁰. – отрицательно определенная в R².

4⁰. не является знакоопределенной, так как при котором Q(x) > 0 (например, х = (1, 0)) и , при котором Q(y) < 0 (например, y = (0, 1)).

Тип квадратичной формы можно определить с помощью следующей теоремы.

Теорема 1.

(а) Квадратичная форма положительно определена все собственные числа матрицы А положительны.

(б) Квадратичная форма неотрицательно определена все собственные числа матрицы А неотрицательны.

Без доказательства.

Вычисление собственных чисел матрицы требует вычисления корней многочлена степени n (характеристического многочлена), что не всегда легко. Есть другой способ определить “знак” квадратичной формы.

2. Критерий Сильвестра положительной определенности.

Для матрицы

рассмотрим n ее миноров

,

,

,

...

,

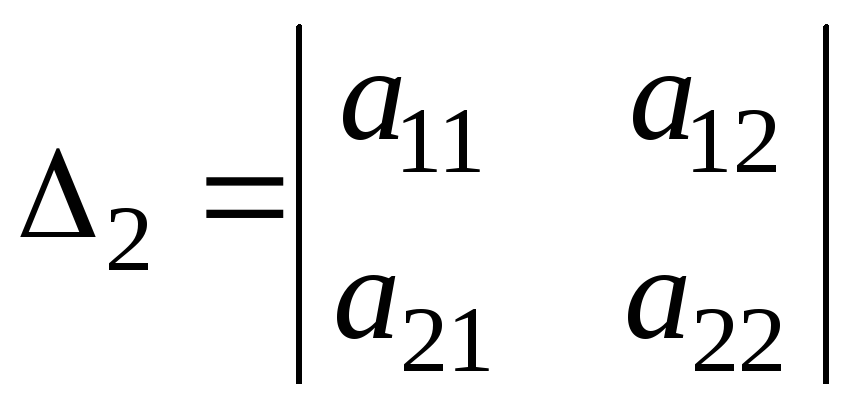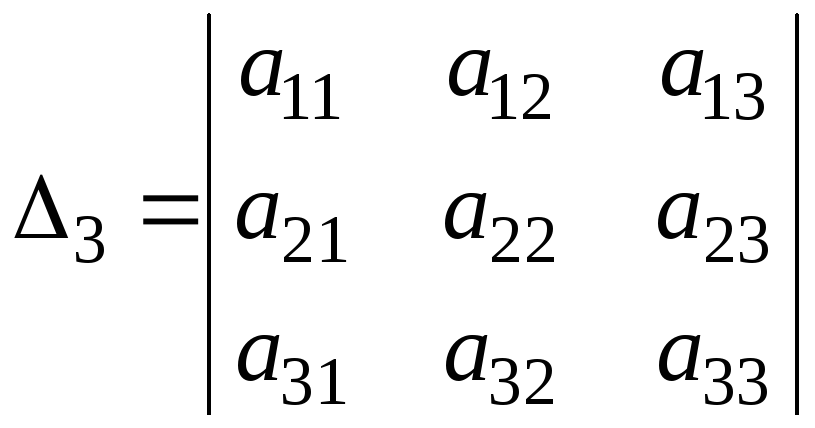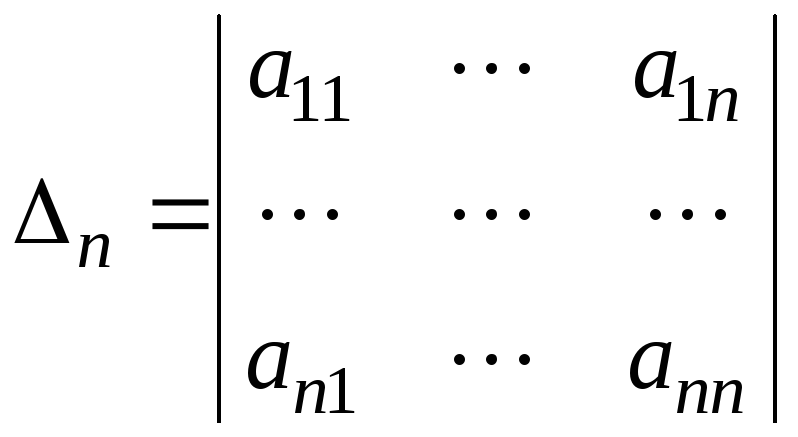которые будем называть угловыми.

Теорема 2 (критерий Сильвестра). (Ах, х) положительно определена , то есть все угловые миноры положительны.

Пример.

.

Удобнее рассмотреть

.

Ее матрица имеет вид

.

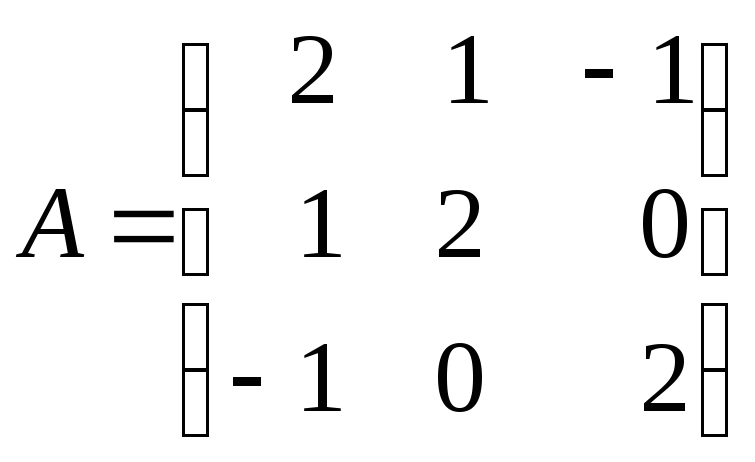Вычислим угловые миноры:

,

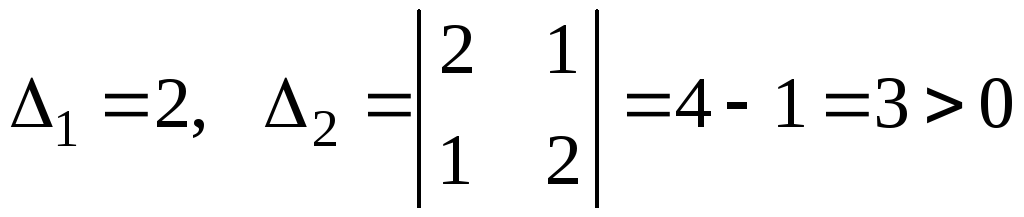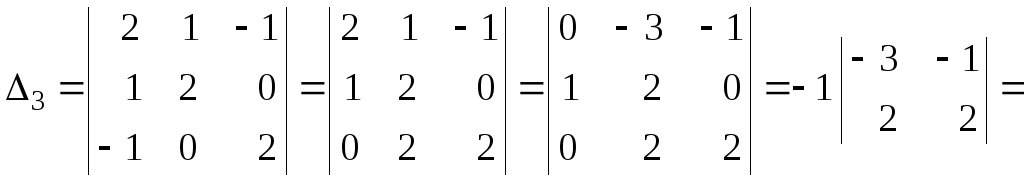
– положительно определена  Q – положительно определена.

3. Критерий неотрицательной определенности.

Определим главный минор порядка k с помощью следующей процедуры:

– выбираем произвольные k элементов на главной диагонали;

– берем строки и столбцы, содержащие эти элементы;

– на их пересечении располагается матрица порядка k. Ее определитель есть главный минор порядка k (определяемый данным набором из k диагональных элементов).

Например, матрица 3-го порядка

имеет

1) три главных минора 1-го порядка

,

2) три главных минора 2-го порядка

,

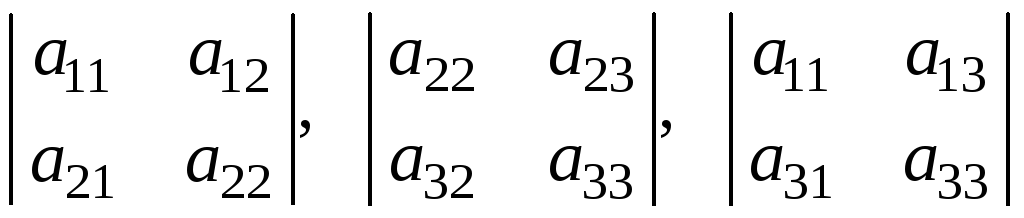3) один главный минор 3-го порядка – это определитель матрицы А.

Теорема 3. Квадратичная форма (Ах, х) неотрицательно определена все главные миноры матрицы А неотрицательны.

Замечание. Из неотрицательности угловых миноров не следует неотрицательность главных миноров (хотя из положительности угловых миноров следует положительность всех главных).

Пример 1.

.

Квадратичная форма не является знакоопределенной, поскольку при , а при . При этом все угловые миноры матрицы квадратичной формы

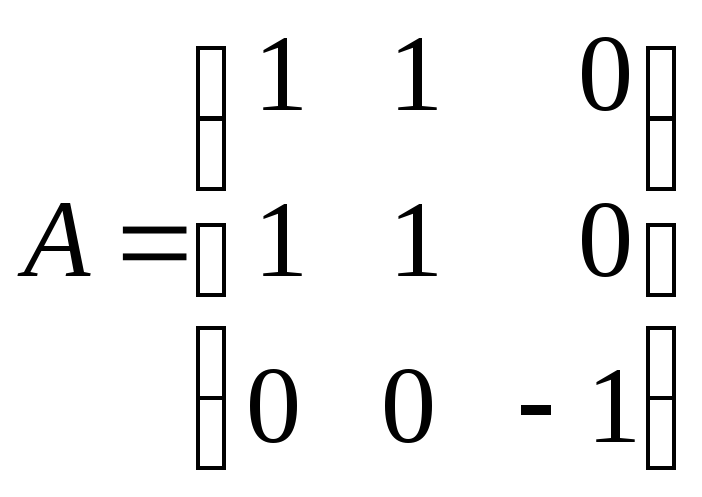
неотрицательны:

,

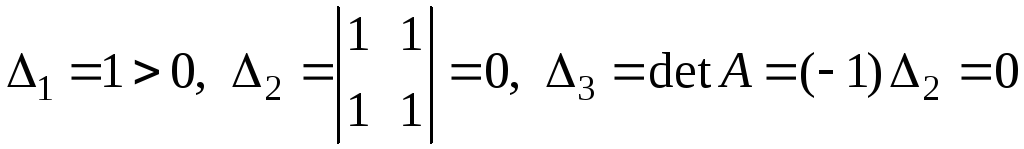но матрица А имеет отрицательный главный минор .

Пример 2.

.

.

Угловые миноры:

, .

Смотрим главные миноры:

а) 1-го порядка – положительны;

б) 2-го порядка: угловой минор и

;

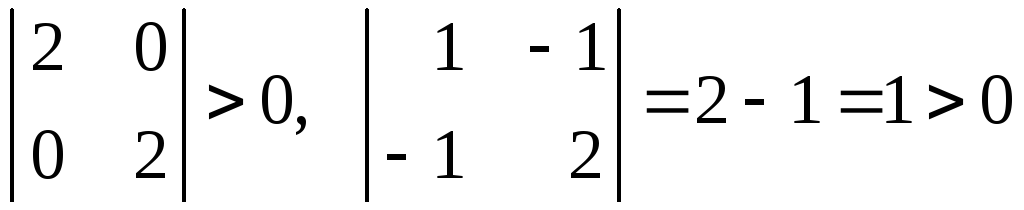в) 3-го порядка: определитель

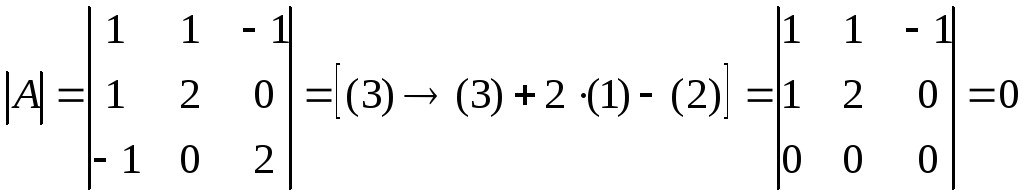
квадратичная форма неотрицательно определена.

Применения линейной алгебры в экономике

1. Модель “затраты – выпуск”.

Имеется предприятие, выпускающее п видов продукции в количествах х₁, х₂, ... , х_п соответственно.

Вектор 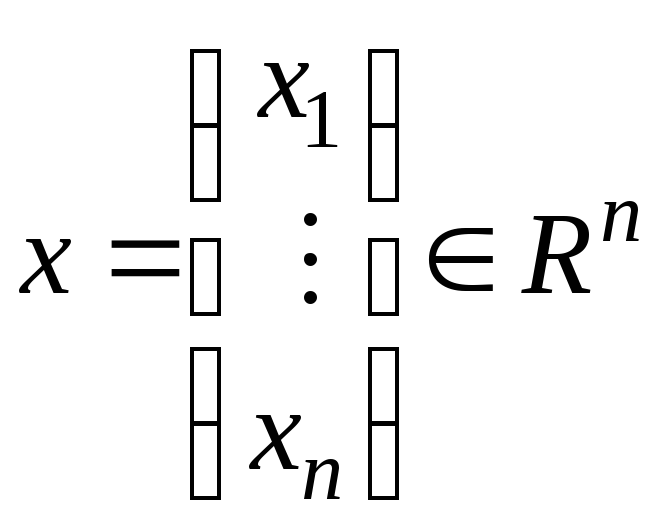называется планом выпуска.

При этом расходуется т видов ресурсов, имеющихся в количествах b₁, b₂, ... , b_m соответственно.

Вектор называется вектором ресурсов.

Известны расходные коэффициенты a_ij – количество i-го ресурса, необходимого для производства единицы j-го продукта, i = 1, ... , m, j = 1, ... , n.

Они образуют матрицу

,

которую называют матрицей расходных коэффициентов, или технологической матрицей. При плане х = (х₁, ... , х_п) расход i-го ресурса составит величину

,

или в матричной форме

,

где у – вектор расхода ресурсов.

Можно рассматривать модель, когда расходы не превышают запасы:

,

то есть

,

где неравенства между векторами понимаются покомпонентно. А можно потребовать, чтобы расходовались все имеющиеся ресурсы. Тогда

,

то есть

.

Рассмотрим последний вариант. Пусть даны запасы ресурсов b и матрица расходных коэффициентов А. Требуется определить план выпуска такой, что

.

Это означает, что надо найти решение линейной системы.

Если т = п и , то решение дается формулой

.

Но, как правило, не все так просто: и, кроме того, нас интересуют планы х, удовлетворяющие дополнительному условию:

,

то есть .

Простой является задача: дан план х, найти расход ресурсов у. Тогда

у = Ах,

то есть для ее решения надо А умножить на х.

2. Модель межотраслевого баланса (модель Леонтьева).

Имеется n отраслей промышленности. Каждая отрасль производит один продукт, который потребляют она сама и другие отрасли, а остаток предназначен для непроизводственного, или конечного потребления.

Рассмотрим процесс производства за некоторый период времени, например, за год.

Обозначим

х_i – общий (валовой) объем продукции i-той отрасли (i = 1, ... , n);

х_ij – объем продукции i-той отрасли, потребляемый j-той отраслью (i, j = 1, ... , n);

y_i – объем конечного продукта i-той отрасли для непроизводственного потребления (i = 1, ... , n).

Все величины – в одних единицах, например, в рублях.

Соотношения баланса имеют вид:

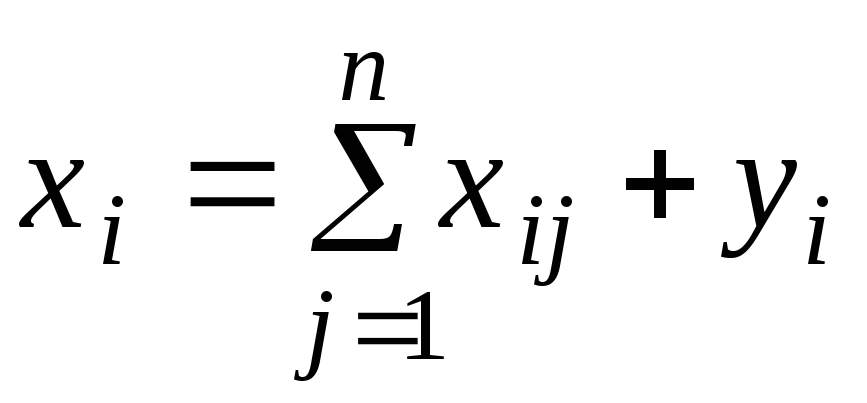, i = 1, ....., n. (1)

Другими словами, общий продукт = продукт, потребляемый n отраслями + конечный продукт.

Введем коэффициенты прямых затрат:

, i, j = 1, ... , n.

Это – затраты продукции i-той отрасли на производство единицы продукции j-той отрасли. Будем считать, что a_ij – постоянны (технологические коэффициенты), то есть не зависят от x_ij, x_j. Тогда имеет место зависимость

i, j = 1, ... , n (2)

– линейная зависимость материальных затрат от валового выпуска.

Подставляя (2) в (1), получаем:

i = 1, ....., n (3)

– линейные балансовые соотношения.

Обозначим

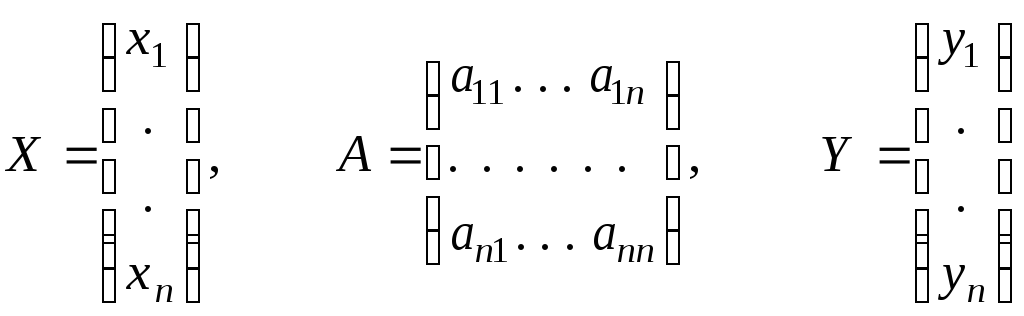
Тогда (3) можно записать в виде:

(4)

3. Основная задача межотраслевого баланса.

Дана матрица прямых затрат А и вектор конечного продукта Y; найти вектор валового выпуска Х.

Перепишем (4) в виде:

, (5)

где Е – единичная матрица.

Пусть матрица (Е – А) – невырождена, то есть . Тогда существует обратная матрица (Е – А)^-1. Умножая (5) на (Е – А)^-1 слева, получаем:

. (6)

Матрица называется матрицей полных затрат.

Из (6) получаем

. (7)

Выясним смысл коэффициентов матрицы

.

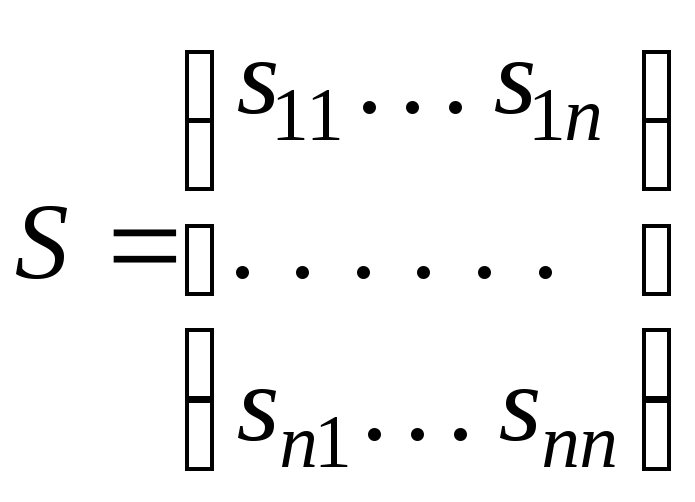Для этого положим Y = Y¹ = (1, 0, ... , 0), то есть требуется получить единицу первого конечного продукта, а остальные – нули. Тогда

.

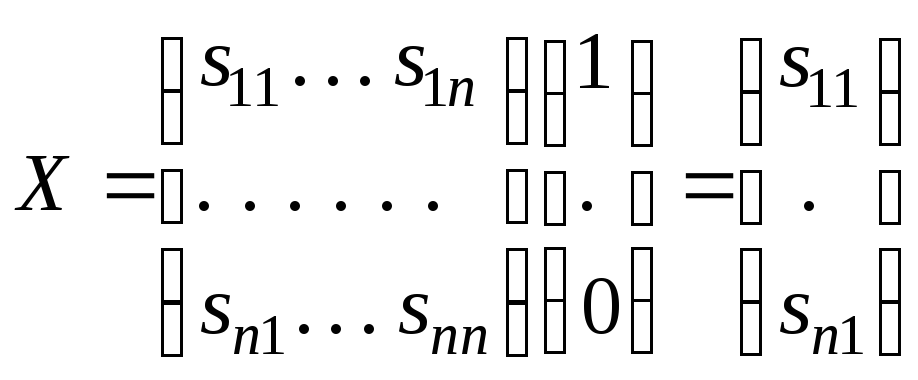Итак, на производство единицы первого конечного продукта каждая отрасль требует

полного выпуска (полных затрат), соответственно. Аналогично, положив

(1 на j-м месте), получаем

,

то есть на выпуск единицы j-го конечного продукта потребуется

полного выпуска (полных затрат) 1-й, 2-й, ... , п-й отрасли, соответственно. Итак, s_ij – количество полных затрат (или валового выпуска) i-той отрасли, необходимых для производства единицы продукта j-той отрасли. Знание матрицы полных затрат позволяет легко найти решение задачи по формуле (7).

4. Продуктивная матрица.

В соответствии с экономическим смыслом задачи должно быть:

.

Здесь означает, что , а означает, что . Кроме того, .

Определение. Матрица А называется продуктивной, если для любого вектора существует вектор , являющийся решением основной задачи межотраслевого баланса:

.

Пусть S = (Е – А)^-1 существует и имеет неотрицательные коэффициенты. Тогда ясно, что

.

Последнее вытекает из правила умножения матрицы на вектор и того факта, что скалярное произведение двух векторов с неотрицательными коэффициентами есть неотрицательная величина. Итак, имеет место

Теорема 1. Пусть S = (Е – А)^-1 существует и имеет неотрицательные коэффициенты. Тогда матрица А продуктивна.

Имеется другой критерий продуктивности, не требующий знания обратной матрицы.

Теорема 2. Пусть А – матрица с неотрицательными элементами a_ij и пусть для любого j-го столбца

,

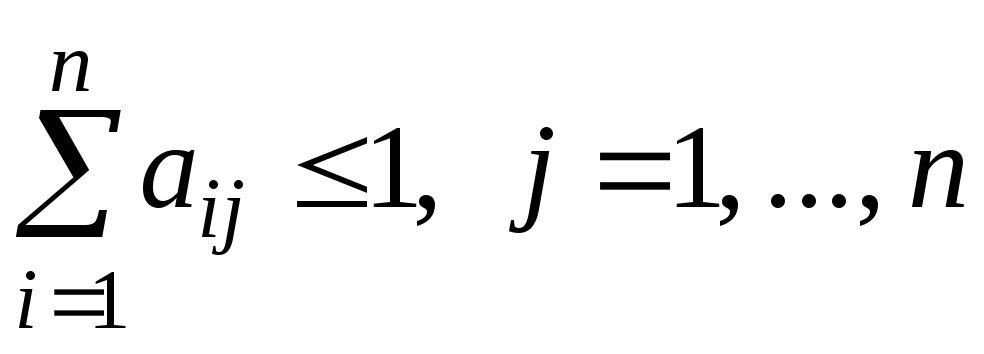причем существует столбец с номером k, для которого

.

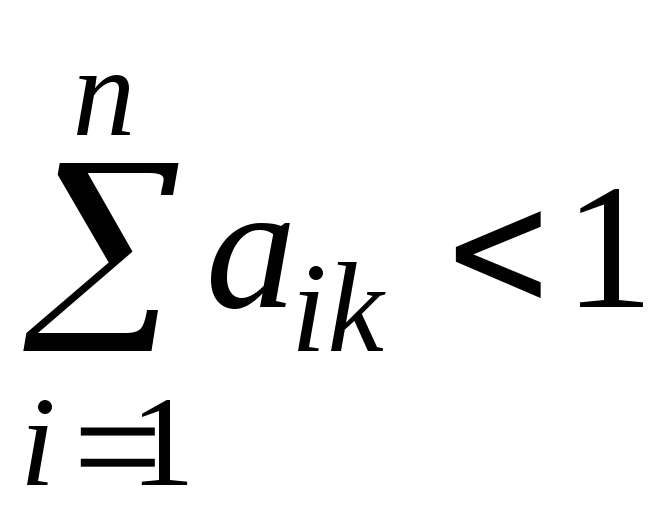Тогда А продуктивна.

5. Пример.

В таблице приведены данные об исполнении баланса за отчетный период в условных денежных единицах:

Потребление Производство	Энергетика	Машино-строение	Конечный продукт	Валовой выпуск
Энергетика Машиностроение	7 12	21 15	72 73	100 100

Требуется вдвое увеличить конечный продукт энергетики, сохранив конечный продукт машиностроения. Каков должен быть новый валовой выпуск каждой отрасли?

Здесь х₁ = 100, х₂ = 100,

х₁₁ = 7, х₁₂ = 21,

х₂₁ = 12, х₂₂ = 15.

Следовательно, коэффициенты прямых затрат равны соответственно

а₁₁ = 0,07, а₁₂ = 0,21,

а₂₁ = 0,12, а₂₂ = 0,15.

Таким образом,

.

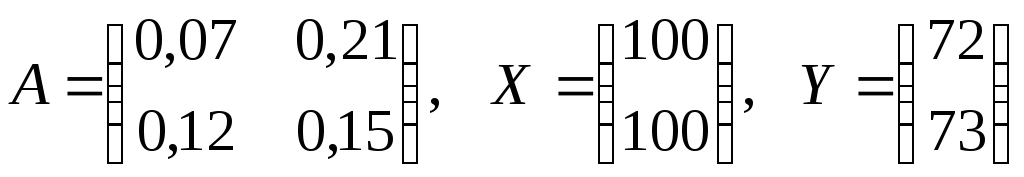Матрица А прямых затрат с положительными коэффициентами имеет суммы столбцов

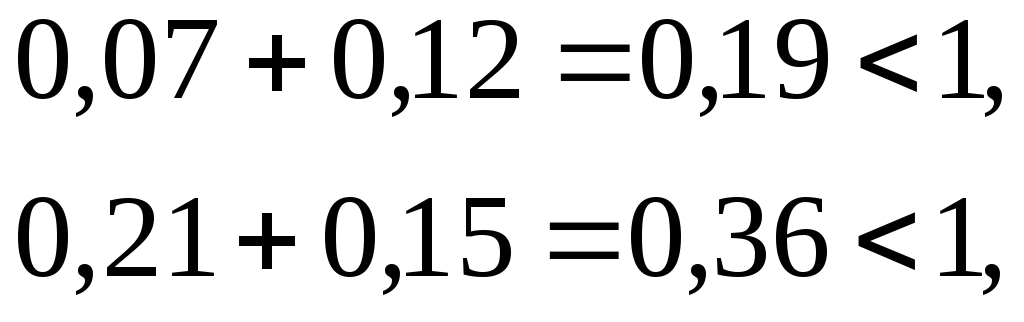
и, следовательно, удовлетворяет условию продуктивности.

Найдем (Е – А)^-1. Имеем

;

.

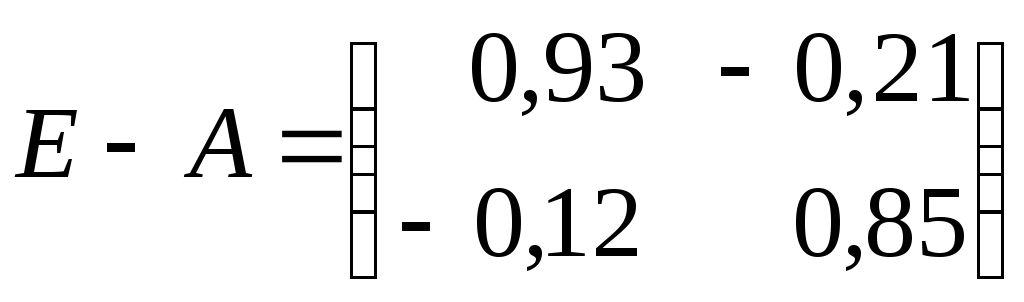Матрица из алгебраических дополнений имеет вид

,

а транспонирование дает:

.

Следовательно,

.

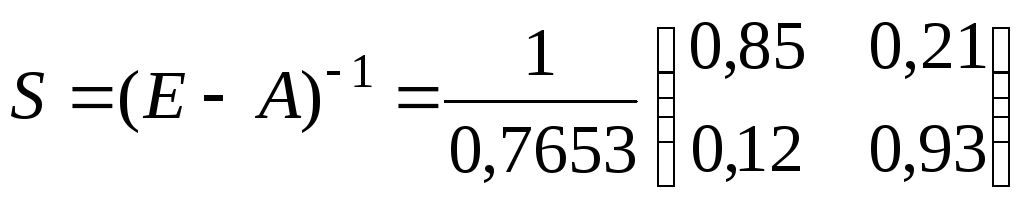По условию новый вектор конечного продукта равен

.

Найдем новый вектор валового выпуска

.

Итак, новые значения валового выпуска будут

(было 100) – энергетика, (было 100) – машиностроение.

Вывод: для увеличения конечного выпуска энергетики вдвое валовой выпуск машиностроения также приходится увеличить (на 11%), а валовой выпуск энергетики надо увеличить всего на 80% (а не на 100%!).