Примеры:

1.Исследовать на экстремум функцию:

Необходимые условия экстремума:

.

Достаточные условия экстремума: составим матрицу из вторых производных:

.

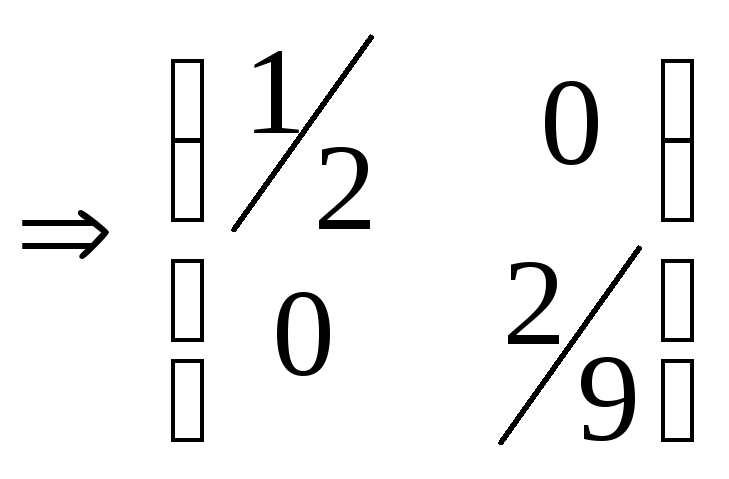Г

лавные миноры положительны, значит второй дифференциал положителен:

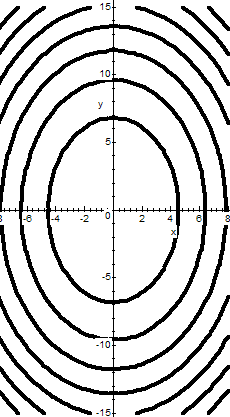
Функция в точке (0,0) имеет минимум. Впрочем, это ясно если построить линии

уровня функции, u =const: (эллипсы). Функциязадает эллиптический параболоид.

2.

Необходимые условия экстремума:

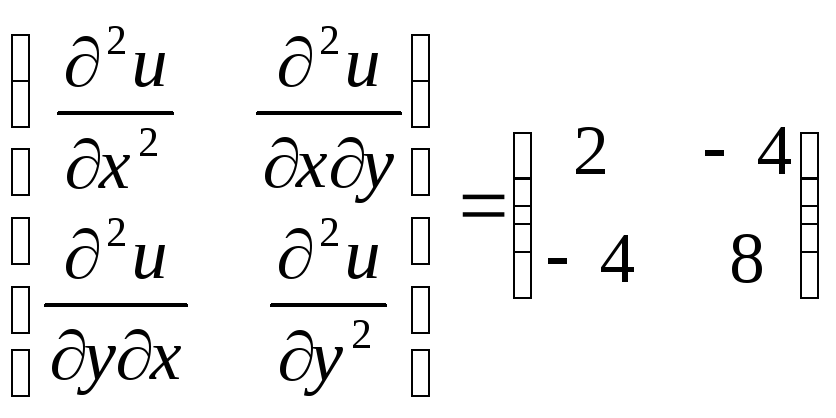
Достаточные условия экстремума: . Второй дифференциал – полуопределён. Обратим внимание на то,что:

при этом ясно, что на линии функция равна нулю, а вне этой линииu> 0. (параболический цилиндр).

§. Наибольшие и наименьшие значения функции в замкнутой области.

Пусть функция определена и непрерывна в ограниченной замкнутой областиD. По теореме Вейерштрасса, функция в этой области достигает наибольшего и наименьшего значения.

Чтобы найти наибольшее и наименьшее значение функции в замкнутой ограниченной области D нужно найти все внутренние точки D «подозрительные» на экстремум и сравнить со значениями функции в граничных точках области. Наибольшее (наименьшее) из этих значений и будет наибольшим (наименьшим) значением функции в области.

Примеры:

1. Найти наибольшее значение функциив треугольнике:.

Получаем: . Внутри областиобращаются в ноль только в точкеНа границах области функцияu= 0.

Наибольшее значение функции u(x,y):

2⁰.Найти наибольшее и наименьшее значение функции:при условии.

а).Из условия:и, исключая изпеременнуюполучим:

. Сформулируем новую задачу:

Найти наибольшее и наименьшее значение функции в кругеx² +y² 1.

;

.

Из необходимых условий следует, что:

а1). x= 0,y= 0; (= 0); а2).x= 0,y=; (= 0,25);

а3). y= 0;x=(= 1); а4).

Последняя система, очевидно, решений не имеет.

б). Теперь надо посмотреть функциюна границе области, т. е. когда:

x²+y²= 1y²= 1 –x²для.

Для нее: и, следовательно :

б1). x= 0; (= 0) б2).x=; (= 0,25).

в). И, наконец, надо посмотреть точкиx = ±1 при этом в1).x= ± 1, (= 0).

Вывод:наибольшее значение функции в области== 1,

наименьшее значение ==== 0.

3.Для функции одного переменного, если внутри промежутка имелось только одна точка локального экстремума, то в ней обязательно достигалось наименьшее либо наибольшее значение. Для функций многих переменных это, вообще говоря, не так.

Δ. Для примера рассмотрим функцию в прямоугольнике:. Необходимые условия экстремума:,.

Отсюда следует: а1). x= 0,y= 0. а2).x= 2,y= 2 – не принадлежат прямоугольнику.

Достаточное условие экстремума в точке (0,0):

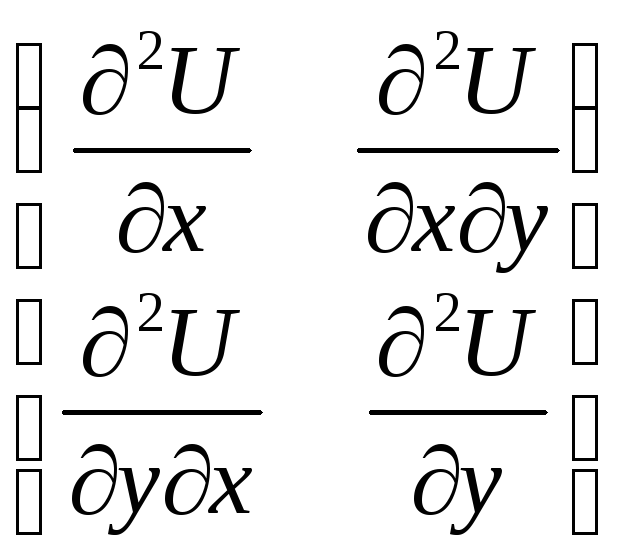=,₁= – 8;₂= 12.

Функция вDимеет локальный максимум. И, при этом,. Однако это значение не является наибольшим в области, ибо:. ▲

§ Функции многих переменных, заданные неявно.

А.УравнениеF(x₁,x₂,…,x_k,y) = 0 в (n+1) – мерном параллелепипеде:

a_i≤x_i≤b_i,i= 1, 2, 3….,n;c≤y≤dопределяетy как однозначную функцию отx_i:

y=y(x₁,x₂, …..x_n), если для любой точки (x₁,x₂, ….x_n) содержащейся вn-мерном параллелепипедеa_i≤x_i≤b_i,i= 1, 2, 3….,nуравнение имеет один и только один кореньyв промежутке [c,d].

T^o.Пусть:

1.F(x₁,x₂,……x_k,y) определена и непрерывна в (n+ 1) – мерном параллелепипеде:

с центром в,

2.Частные производные(i=1, 2,…..,n) исуществуют и непрерывны вD,

3.,4. .

Тогда:

а.В некоторой окрестностиуравнениеопределяетукак однозначную функциюy=f(x₁,x₂,…x_n),

б.При этом,,

в.Функцияy=f(x₁,x₂,…x_n) непрерывна по всем своим аргументам,

г.И имеет непрерывные частные производные,, …..,.

Б.При каких условиях, в общем случае, системаmуравнений:

(*)

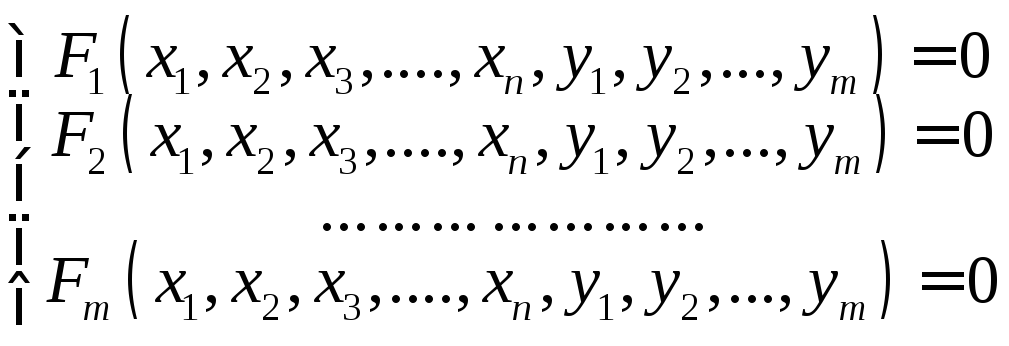определяет y₁,y₂,…,y_mкак однозначные функции: ?

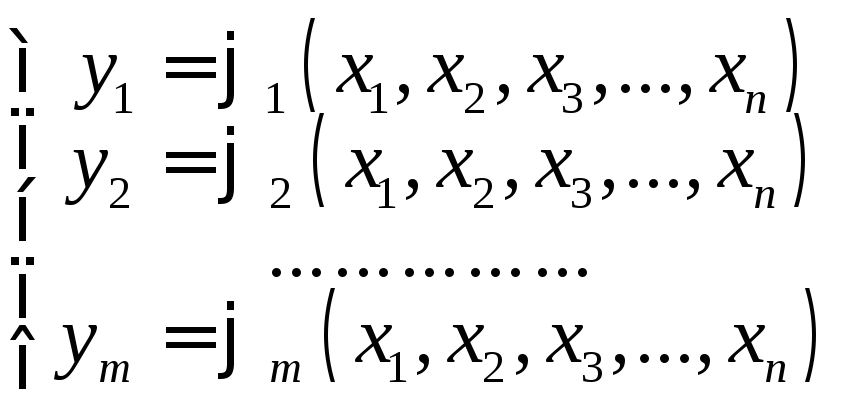Ответ на этот вопрос дает следующая теорема, которая вместе с предыдущей носит название теоремы о неявных функциях.

T^o.Пусть:

1.Все функцииF₁(..),F₂(…), ….F_m(…) определены и непрерывны в (n+m) мерном параллелепипеде:

с центром в точке ,

2.Существуют и непрерывны вD частные производные всех функцийF_j (…) по всем аргументам,

3.Точкаудовлетворяет всем уравнениям системы (*),

4.ЯкобианJсистемы в этой точке отличен от нуля.

J==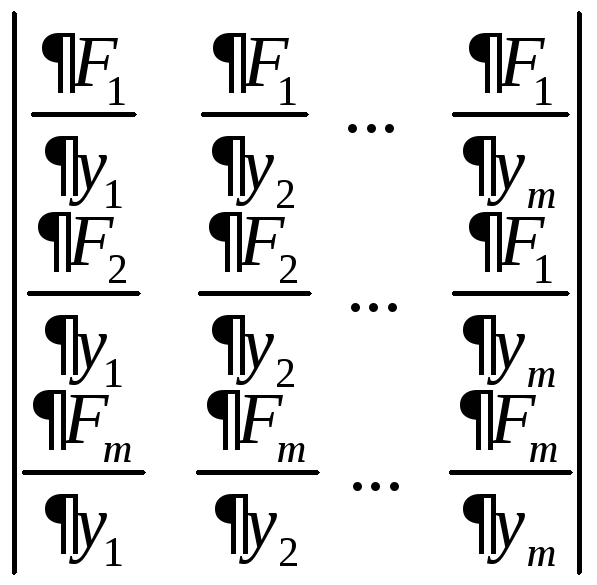0.

Тогда:

а.В некоторой окрестности точкисистема уравнений (*) определяетy₁=f₁ (x₁,x₂,…x_n),y₂=f₂(x₁,x₂,…x_n),…,y_m=f_m(x₁,…,x_n), как однозначные функции от аргументовx₁,x₂, ….,x_n,

б.При этом,y_j⁰=f_j(x₁⁰,x₂⁰, …,x_n⁰),j = 1, 2, …,m,

в.Функцииf₁,f₂, ….,f_mнепрерывны в точке (x₁⁰,x₂⁰, …,x_n⁰),

г.И имеют непрерывные частные производные по всем аргументам.