§. Дифференциалы высших порядков.

Определение nдифференциала индуктивное:.

Пусть Тогда:

Найдем второй дифференциал. =

= =

=

= +

+ .

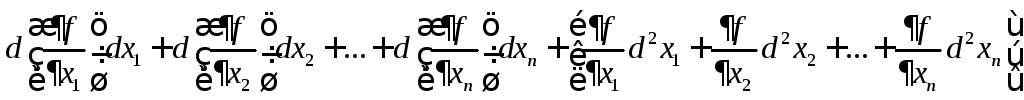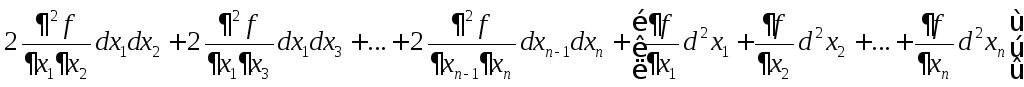Для второго дифференциала получена формула:

В этой формуле выражение в квадратных скобках в правой части отсутствует, если – независимые переменные, и присутствует если

Это показывает, что форма второго дифференциала не инвариантна относительно замены переменных.

Формула для формального запоминания второго дифференциала для функции nнезависимых переменных имеет вид:.

а для дифференциала k^-гопорядка:

Замечание:Обратим внимание на то, что если функциилинейны т.е. имеют видто второй дифференциал и более дифференциалы более высокого порядка инвариантны по форме.

§. Формула Тейлора.

Напоминание:Для функции одного переменногоF(t) ранее была получена формула ее разложения в ряд Тейлора (по формуле Тейлора) в дифференциальной форме:

, где величина.

При этом, – в левой части иdt ­– в правой части совпадают.

В этом виде формула Тейлора справедлива и для функций нескольких переменных.

В дальнейшем, для упрощения письма ограничимся рассмотрением функции двух переменных .

Т. Пусть u = f (x,y) определена и непрерывна в некоторой окрестности точки и имеет в этой окрестности непрерывные производные до (n+1)^-го порядка включительно. Пусть итаковы, что точкапринадлежит указанной окрестности.

Тогда: =

= , где. При этомв левой части, совпадают сdx и dy в правой части.

Δ. Соединим точки Р и Р₀ прямолинейным отрезком, принадлежащим упомянутой в формулировке теоремы, окрестности: ;;.

Подставляя это в , получим.

Тогда: =

= , где .

При этом dtв правой части равенства равно Δt=1–0 =1.

Теперь воспользуемся тем, что при линейной замене переменных высшие дифференциалы инвариантны по форме. (*)

Аналогично для ,,…,и.

Подставляя в формулу (*) получаем требуемое. ▲

§ Экстремумы функций нескольких переменных.

Def: Пусть определена в области D ивнутренняя точка областиD.Если

то говорят, что в точке функция имеет локальный максимум. Если– локальный минимум, строгий или нет.

Необходимое условие экстремумафункции нескольких переменных:

Пусть имеет в точкеконечные

У функции зафиксируемПолучимТогда функциякак функция одного переменногоимеет по

экстремум и, следовательно,. Аналогично

Итак:необходимым условием экстремума дифференцируемой функции

является равенство нулю всех ее частных производных, т.е. точки «подозрительные» на экстремум удовлетворяют системе уравнений:

.

§. Достаточные условия экстремума.

Пусть определена, непрерывна и имеет непрерывные производные первого и второго порядка в некоторой окрестности стационарной точки. Тогда:

Разложим функцию в ряд Тейлора в окрестности стационарной точки.

=.

(При этом .– вычислены в точке,.

Обозначая , получим, где

при , и, следовательно,

.

В силу того, что второе слагаемое в скобках бесконечно мало по сравнению с первым, знак приращения определяется знаком второго дифференциала функции (если он не обращается в нуль). Следовательно от знака второго дифференциала зависит наличие экстремума функции в исследуемой точке.

В алгебре:

Def. Вещественно значная функция векторного аргументаназывается квадратичной формой, а квадратная матрица– матрицей квадратичной формы.

Из определения квадратичной формы ясно, что второй дифференциал функции является квадратичной формой , матрица которой состоит изОт свойств этой квадратичной формы и зависит имеет ли функция экстремум в рассматриваемой точке или нет.

Def.Квадратичная форманазывается положительно определённой, если она принимает положительные значения при всех значениях аргументов, не равных нулю одновременно., причем.

Def.Квадратичная форманазывается отрицательно определённой, если.

Def.Квадратичная форма называется полуопределённой, если

(или ).

Def.Квадратичная форма называется неопределённой, если

и.

Критерий Сильвестра :Для того чтобы квадратичная форма была положительно определённой необходимо и достаточно, чтобы все главные миноры матрицы квадратичной формы были положительны. Для того чтобы квадратичная форма была отрицательно определённой необходимо и достаточно чтобы главные миноры матрицы квадратичной формы чередовались по знаку начиная с минуса:

Если миноры будут ++++… или –+–+… но среди них встречаются нулевые то форма будет полуопределённой. Δ▲.

Пример:Формаимеет матрицу:

А=. Ее миноры:

Все миноры положительны, форма положительно определена . В самом деле, нетрудно проверить, что: .

Т. Если квадратичная формат.е. второй дифференциал функции,

будет положительно определённой то функция, в испытуемой точке, функция будет иметь минимум; если отрицательно определённой то функция будет иметь максимум.

Если форма полуопределена, то для ответа на вопрос о экстремуме функции требуется привлечение производных более высокого порядка. Во всех остальных случаях – экстремума нет. Δ▲.