§. Производная сложной функции.

Т⁰.Если– функция дифференцируемая в точкеР₀и функциидифференцируемы вt₀, то функциядифференцируема в точкеt₀и

.

Δ. =

= =.

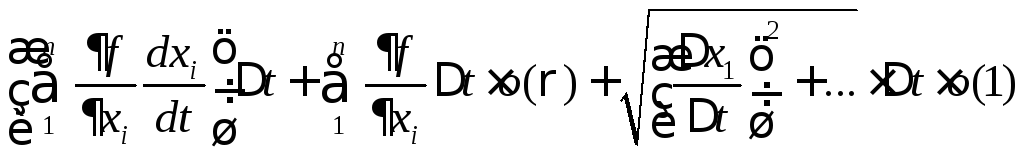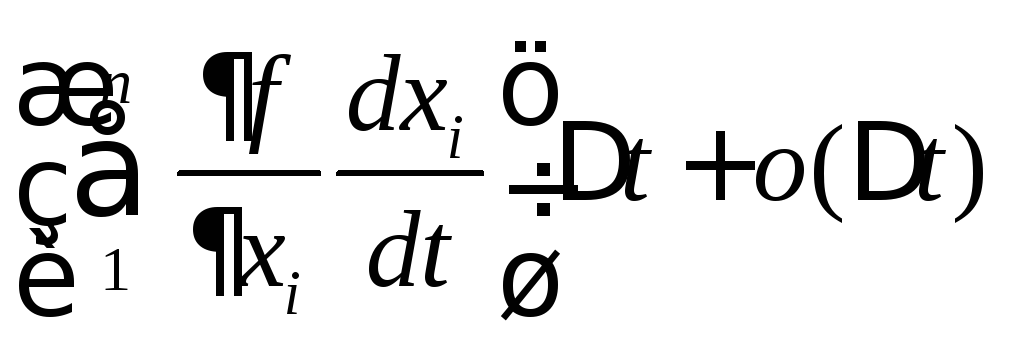Это и доказывает дифференцируемость функции и

. ▲

Без труда можно доказать и формулы для дифференцирования сложной функции и в более общем случае:

Пусть и. Тогда длясправедливо:.

Примеры.

1⁰. Пустьи. Найтии.

;.

2⁰. (контрпример). Пустьи. Найти.

а);б).

Получили результаты, противоречащие один другому. Этот случай показывает, что формула производной сложной функции в этом случае не работает.

NB. Оказывается существование частных производных недостаточно для дифференцируемости (хотя наоборот верно). Дифференцируемость более жесткое требование, чем существование частных производных.

§. Формула конечных приращений для функции многих переменных.

=

= =

= .

Δ. Доказательство основано на возможности соединить точки иРпрямолинейным отрезком, принадлежащим области. ▲

§. Производная функции по направлению.

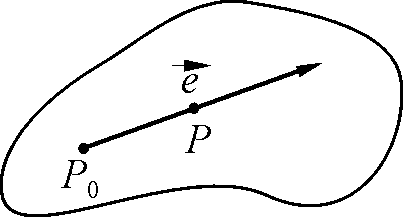
Пусть задана функция трех переменныхи в пространстве задано направление. Производной функциипо направлениюназывается .

Запишем параметрическое уравнение прямой проходящей через точки Р иР₀:

;:.

Тогда: и, значит

.

Если ввести в рассмотрение вектор то получим.

Значит , где- угол между направлениеми направлением.

Следовательно, показывает направление наискорейшего возрастания функцииf, а его длина совпадает со скоростью возрастания функции в этом направлении.

§. Инвариантность формы 1го дифференциала при замене переменных.

Пусть , и.

Тогда и

===

= =

= = .

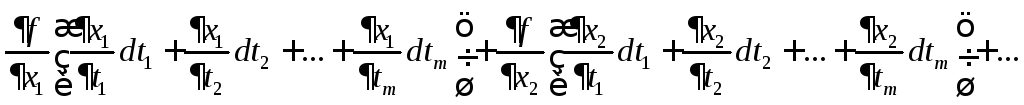То есть: .

Последняя формула выражает свойство инвариантности формы первого дифференциала относительно замены переменных.

§. Производные высших порядков.

Определение производной более высокого порядка, чем первый, можно дать индуктивно. Обозначения для высших производных: .

Пример:

1⁰.Найти частные производные первого и второго порядка функции.

Производные первого порядка: ;;.

Производные второго порядка:

;;;

;;;

;;.

Производные называются вторыми одноименными производными.

Обозначение обозначает, что от функциипроизводная бралась вначале по, а затем по, а при нахождениинаоборот, вначале по, а затем по.

Обратим внимание на совпадения соответствующих вторых смешанных производных:

.

Возникает вопрос: случайно ли это совпадение?

2⁰.Рассмотрим функцию, заданную соотношениями:

и.

Функция непрерывна в (0,0) т.к. 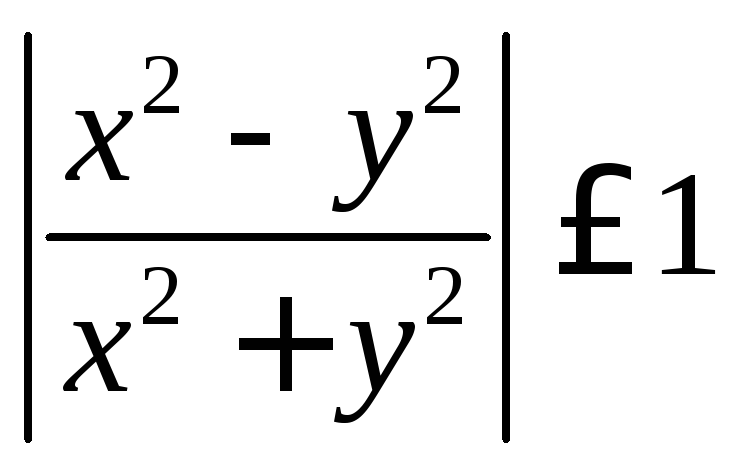и, следовательно,.

а) .б) .

в) .

Если в положитьх = 0, получим,в (0,0).

г).

Полагая y= 0, получим,в (0,0).

Получили, что в точке (0,0). Смешанные производные в точке (0,0) не совпадают.

Итак, вторые смешанные производные не всегда совпадают. А когда?

Т.Пустьопределена в открытой областии в этой области, существуют, а такжеи, наконец,непрерывны в некоторой точке. Тогда:.

Δ. Рассмотрим .

а).Введем вспомогательную функцию. Эта функция дифференцируема:и, следовательно, непрерывна.

Учитывая это, получим:

= = =…

Дважды применим формулу конечных приращений:

…= =.

б)Введем. Тогда аналогично получаем, что

.

Устремим и воспользовавшись непрерывностьюв точкеполучаем:. ▲

В общем случае:

Т⁰.Пустьопределена в открытой областиевклидового пространстваЕ_nи имеет в этой области всевозможные частные производные до (n-1)^гопорядка включительно и смешанные производныеn^гопорядка, причем все производные непрерывны в области. Тогда значение любойn^йсмешанной производной не зависит от того порядка, в котором производится дифференцирование. Δ▲.