Раздел 8. Функции многих переменных. §. Воспоминания о будущем.

Пусть V_n– линейное пространство.

Def.: В множествеRвведено скалярное произведение, еслитакое, что:;;

;.

Если в линейном пространстве V_nвведено скалярное произведение, то пространство называетсяевклидовымпространством (в дальнейшем евклидово пространство, зачастую, будет обозначаться.

Def.:В множествеRвведена норма, если, такое, что:

;;.

Линейное пространство V_n, в котором введена норма называется нормированным пространством.

Def.В множествеRвведена метрика, еслитакое, что

;;.

Если в множестве Rвведена метрика, тоRназывается метрическим пространством.

Если в пространстве V_nвведено скалярное произведение (V_n–евклидово пространствоE_n), то в нем можно естественным образом ввести нормуи метрику.

Говорят что, норма и метрика индуцируются скалярным произведением.

Пусть E_n– евклидово пространство с индуцированными нормой и метрикой, и– ортонормированный базис вE_n.

Тогда: .

Def: открытый шар.

замкнутый шар.

сфера

открытый параллелепипед

замкнутый параллелепипед.

Def: – ε - окрестность точких₀.

– проколотая ε - окрестности точких₀.

– прямоугольная окрестность точких_0.

проколотая прямоугольная ε - окрестность.

F

°.Любая ε – окрестность точки содержится в некоторой прямоугольной окрестности той же точки и, наоборот, содержит в себе некоторую прямоугольную окрестность той же точки.

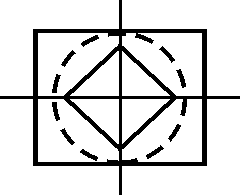
Факт этот свидетельствует о том что, топологии введенные с помощью прямоугольных и сферических окрестностей эквивалентны.

Аксиома полуотделимости:Из любых двух точек евклидового пространства каждая имеет окрестность, не содержащая другую точку.

Аксиома отделимости: Для любой пары точек евклидового пространства существуют их непересекающиеся окрестности.

Def:ТочкаР(х₁, ….,х_n) называется внутренней точкой множестваМ, если.

Def:ТочкаРназывается граничной точкой множестваМ, если

.

Def:ТочкаРназывается предельной точкой множестваМ(или точкой сгущения), если

.

Def:МножествоМназывается открытым, если все его точки внутренние.

Def:МножествоМназывается ограниченным, если.

Def:Если, то говорят, что в множестве М задана кривая. КриваяL:называется непрерывной, если- непрерывные функции.

D

ef:МножествоМназывается связным, если любые его точки можно соединить непрерывной кривой, все точки которой принадлежат множествуМ.

Def:МножествоМназывается односвязным, если любой замкнутый контур в множествеМможно непрерывным движением стянуть в точку принадлежащую множествуМ.

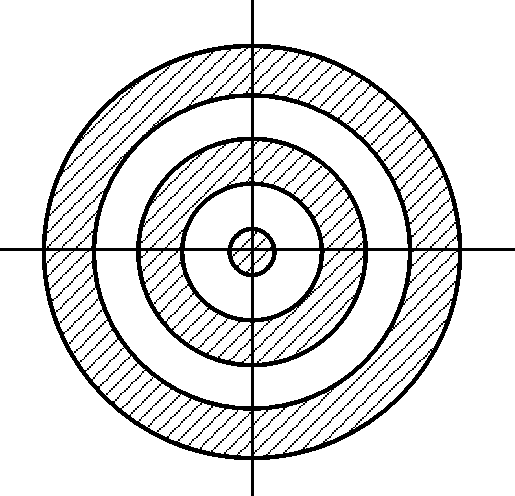
Пример:область определения функции– круг радиуса 2 с центром в начале координат – связна, а область определения функции– концентрические кольца (см. рис.) –не связна:

.

Def:Последовательностьточек евклидового пространства называется сходящейся, к элементу пространстваР, если.

Тº. Для того, чтобынеобходимо и достаточно, чтобы последовательности координат сходились к соответствующей координате т.Р.

Δ 1) Пусть , т.е.

.

2) Пусть последовательность, тогда, и значит▲

Def:Последовательностьточек евклидового пространства называется фундаментальной, если.

Тº.Для того, чтобы последовательностьсходилась необходимо и достаточно, чтобы она была фундаментальной.

Δ. Доказательство основано на переходе к покоординатной сходимости и ссылке на то, что для числовых последовательностей этот факт доказан. ▲

Тº. (Больцано - Вейерштрасса) Из любой бесконечной ограниченной последовательности точек евклидового пространства можно выделить сходящуюся подпоследовательность.

Δ Задана бесконечная, ограниченная последовательность , такая, что. Рассмотрим последовательность первых координат элементов

этой последовательности . Это бесконечная и ограниченная числовая последовательность и, следовательно, из нее можно выделить сходящуюся подпоследовательность. Тем самым, из последовательностивыделена подпоследовательность, у которой последовательность первых координат сходится. Обозначим элементы этой последовательности вновь.

Далее рассмотрим последовательность вторых координат элементов этой последовательности , и проведем ту же процедуру. … Проделав эту процедуруmраз (m– размерность евклидового пространства), в конце концов, получим последовательностьс покоординатной сходимостью. Следовательно, построенная последовательность сходится. ▲