§21.Матрицы и действия над ними. Линейное пространство матриц

Матрицей n  m называется прямоугольная таблица , где а_ij – принадлежат некоторому числовому полю K и называются элементами матрицы A или матричными элементами А. Иногда пишут А_nm. Здесь индексы определяют размеры матрицы А (1^й – количество строк, 2^й – количество столбцов). Матрицы А и В называются равными (А = В), если их размеры совпадают и а_ij = b_ij.

На множестве матриц одинаковых размеров можно определить операцию сложения: C = A + B так, что c_ij = а_ij + b_ij, и операцию умножения на скаляр из внешнего поля К: D = A  d_ij = а_ij.

1. Множество матриц А_nm с так определенными операциями поэлементного сложения и умножения на скаляр образуют линейное пространство К_nm. Доказать самостоятельно.

При этом dimK_nm = nm, а базис образуют матрицы E_ij , у каждой из которых элемент, стоящий на пересечении i-ой строчки и j-ого столбца равен 1, а остальные элементы равны 0. Нейтральным элементом является матрица  у которой все элементы равны 0.

Если у матрицы А_nm n = m ,то матрица А называется квадратной, а число n называют порядком этой матрицы. При этом если для еe элементов а_ij = а_ji – матрица называется симметрической (или симметричной), а если а_ij = –а_ji, то матрица называется кососимметрической (или кососимметричной).

2. Всякая квадратная матрица может быть разложена в сумму симметрической и кососимметрической матрицы.

◀ Пусть матрица А_nm задана своими элементами: A_nm = (а_ij), i = 1, 2, …, n, j = 1, 2, …, m. Построим матрицы S_nm и элементы, которых связаны са_ij следующими соотношениями . При этомs_ij = s_ji и . Т.е. матрицыS_nm и соответственно симметричная и кососимметричная. Кроме того

, т.е. А = S +.▶

3. Множество симметричных (кососимметричных) матриц порядка n образуют линейное пространство. Самостоятельно установите базис и размерность этих пространств.

§22. ЕщЕ действия над матрицами

а) Произведение матриц С_nk = A_nmB_mk определим по правилу: c_ij =(это правило в обиходе называется: умножение строка на столбец).

Пример: , но. Из определения произведения матриц ясно, что матрицы можно умножать не всегда, а только если количество элементов в строке 1^ой матрицы и количество элементов в столбце 2^ой матрицы совпадают. Кроме того, видно, что операция умножения матриц, вообще говоря, не коммутативна.

Можно отметить следующие свойства операции умножения матриц:

а1) А(ВС) = (АВ)С – ассоциативный закон;

а2) А(В + С) = АВ + АС – левый и

а3) (А + В)С = АС + ВС правый дистрибутивные законы.

Def: Если в линейном пространстве V над полем К, корректным образом, введена еще одна внутренняя операция, удовлетворяющая свойствам:

⊙(х⊗у) = (⊙х)⊗у = х⊗(⊙у);

х⊗(у⊗z) = (х⊗у)⊗z; 3) (х ⊕ у)⊗z = х⊗z ⊕ у⊗z,

то линейное пространство над полем К называется алгеброй.

Таким образом, определив операцию умножения матриц, удовлетворяющую свойствам а1), а2), а3) мы можем говорить об алгебре матриц (для квадратных матриц).

б) Транспонирование матриц А^Т  =а_ji.

Пример: .

Свойства операции транспонирования:

б1) (А)^Т = А^Т;

б2) (А + В)^Т = А^Т + В^Т;

б3) (АВ)^Т = А^ТВ^Т.

в) Для матриц с комплексными элементами – операция комплексного сопряжения. .

г) Для матриц с комплексными элементами – операция эрмитового сопряжения. (для операции эрмитового сопряжения, математики чаще употребляют значокА^*, а физики А⁺).

Свойства операции эрмитового сопряжения:

г1) ; г2); г3);

г4) ; г5).

Примеры: ;;;.

Элементы а₁₁, а₂₂, …, a_nn – называются диагональными (главными диагональными) элементами матрицы.

Если i > j a_ij = 0 матрица называется матрицей нижнего треугольного вида, если i < j a_ij = 0 – матрицей верхнего треугольного вида:

; .

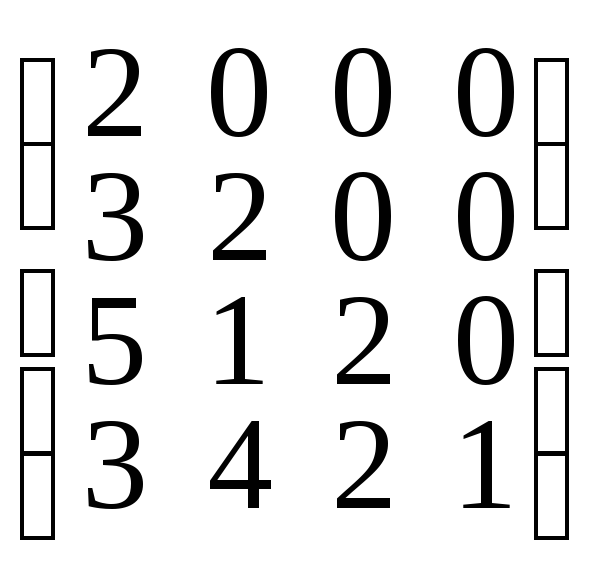нижний верхний

треугольный треугольный

вид вид

Примечание: Если А^* = А, то матрица называется эрмитовой (самосопряженной).

В вещественном пространстве матрица А, удовлетворяющая условию: АА^Т = А^ТА = Е называется ортогональной, а комплексном пространстве – унитарной.