Экзаменационные задачи по курсу "высшая алгебра" . Часть I

1. Образуют ли линейное пространство все функции вида , гдеи- произвольные числа?

2. Образуют ли линейное пространство все непрерывные функции, обращающиеся в 3 при ?

3. Образуют ли линейное пространство все непрерывные функции, обращающиеся в 0 при ?

4. В пространстве полиномов степени не выше 3, является ли подпространством совокупность полиномов у которых ?

5. Найти базис и размерность подпространства многочленов, степени не выше , удовлетворяющих условию:.

6. Найти базис и размерность подпространства полиномов, степени не выше и удовлетворяющих условию:.

7. Найти базис и размерность линейной оболочки, натянутой на векторы: .

8. Найти размерность линейного подпространства, порожденного векторами: .

9. Найти размерность и базис линейной оболочки, натянутой на систему векторов: а) ;

б) .

10. Найти координаты вектора в базисе

.

11. Показать, что векторы образуют базис и найти координаты векторав этом базисе.

12. Найти координаты полинома в базиселинейного пространства полиномов степени не выше.

13. Найти координаты вектора в ортогональном базисе, если.

14. Являются ли векторы линейно независимыми или не являются?

15. Найти угол между векторами и, если

.

16. Найти матрицу Грамма системы векторов , если

.

17. Найти матрицу Грамма системы векторов , если

.

18. Ортогонализовать следующие системы векторов, которые заданы своими координатами в стандартном ортонормированном базисе:

а) ;

б) ;

в) .

19. В пространстве полиномов степени не выше 2, введено скалярное произведение: . В этом пространстве ортогонализовать систему векторов.

20. Ортогонализовать векторы , если.

21. Проверив, что билинейная форма определяет скалярное произведение, в этом скалярном произведении ортогонализовать системы векторов:

а) ;

б) .

22. Ортогонализовать следующие системы векторов с указанными скалярными произведениями:

а) ,;

б) ,;

в) ,;

г) ,.

23. Дополнить следующие системы векторов до ортонормированного базиса:

а) ;

б) ;

в) .

24. Найти произведение матриц:

а) ; б).

25. Найти ранг матрицы:

а) ; б); в).

26. Найти ранг и базисный минор матрицы:

а) ; б).

27. Найти матрицу, обратную к заданной матрице:

а) ; б); в).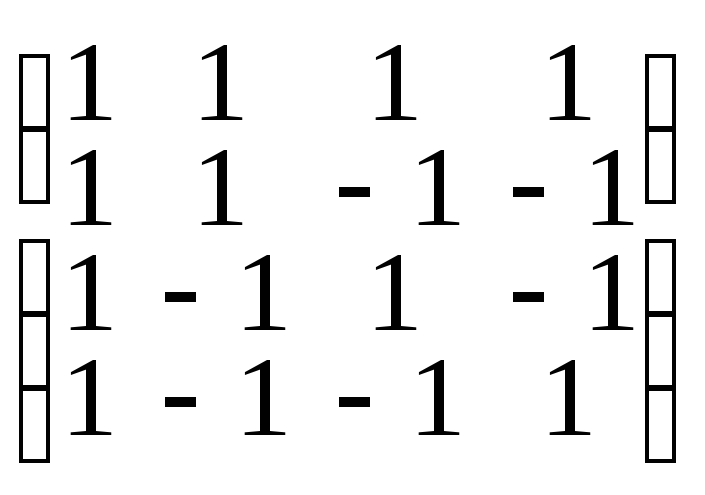

28. Вычислить , если:

а ) , б), в)

; ;.

29. Решить матричные уравнения:

а) ; б);

в) ; г).

30. Сколько миноров k ^-го порядка содержат определитель порядка ?

31. Пользуясь теоремой Лапласа, вычислить определители:

а) ; б); в).

32. Вычислить определители

а) ; б); в).

33. Решить уравнения:

а) ; б).

34. Найти общее решение следующих однородных систем линейных уравнений:

а) ; б); в);

г) ; д).

35. Решить систему по правилу Крамера: .

36. Решить следующие системы неоднородных уравнений:

а) ; б);

в) .

37. Подобрать так чтобы система уравнений имела решения:

а) ; б).

38. Будет ли линейным оператором в пространстве всех многочленов оператор дифференцирования?

39. Доказать, что оператор в трехмерном пространстве, где- постоянный вектор, является линейным оператором.

40. Найти матрицу оператора в указанном базисе пространства полиномов степени не выше:

а) ; б).

41. Найти матрицу оператора в базисе.

42. Найти матрицу оператора в базисе.

43. Доказать, что оператор является линейным и отображает пространство(функций, интегрируемых на) на пространство многочленов первой степени оти. Найти матрицу этого оператора в подпространстве, базисом которого является система векторов.

44. Найти собственные значения и собственные векторы линейного оператора, заданного своей матрицей:

а) ; б); в); г);

д) ; е); ж).

45. Дана матрица 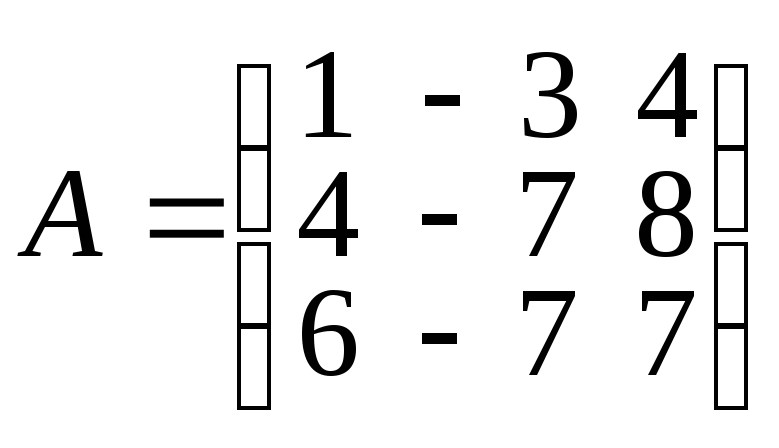и полином. Найти собственные числа и собственные векторы оператора.

46. Найти матрицу билинейной формы в базисе

.

47. Найти матрицу билинейной формы в базисе

e₁(1,-1,1), e₂(1,1,-1), e₃(1,-1,-1).

48. Найти матрицу билинейной формы в базисе

e₁(1,-1,1), e₂(1,1,-1), e₃(1,-1,-1).

49. Найти матрицу билинейной формы в базисе.

50. Определить число положительных и отрицательных канонических коэффициентов для квадратичной формы: .

51. Найти все значения параметра , при которых следующие квадратичные формы являются положительно определенными:

а) ;

б) ;

в) ;

г) .

52. Привести следующие квадратичные формы к каноническому виду:

а) ;

б) ;

в) ;

г);

д) ;

е) ;

ж) ;

з) ;

и) .

53. Найти ортогональную проекцию и ортогональную составляющуювекторана подпространство, порожденное системой векторов:

а) ;

б) ;

в) .

54. Найти ортогональную проекцию и ортогональную составляющуювек­­торана подпространство, определяемое системой уравнений.

55. Найти проекцию вектора на подпространство с базисом, если скалярное произведение имеет вид:.

56. Найти проекцию вектора на подпространство с базисом, если скалярное произведение имеет вид:.

57. Найти угол между вектором и линейной оболочкой:

а) ;

б) .

58. Найти угол между вектором и линейным подпространством, натянутым на векторы:

а) ;

б) ;

в) ;

г) .

59. Найти расстояние между вектором и линейной оболочкой векторов.

60. Найти расстояние между вектором и линейным подпространством, решений системы:.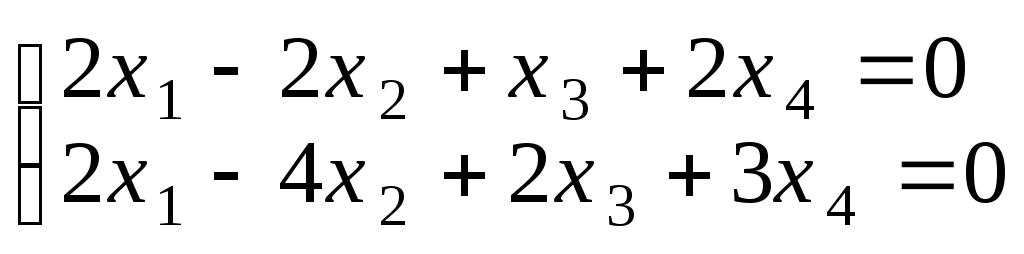

61. Найти расстояние от вектора до гиперплоскости, заданной системой уравнений:.

62. Составить формулы преобразования координат при переходе от базиса к базису.

63. В стандартном базисе найти матрицу оператора, переводящего векторы в векторысоответственно:

а) ;

б) .

64. Найти матрицу перехода от базиса к базисупространства многочленов степени не выше.

65. Каковы будут координаты векторов и, если векторы нового базиса выражаются через векторы старого базиса по формулам:.

66. Линейный оператор в стандартном базисе задан матрицей . 67. Найти матрицу указанного линейного оператора в базисе.

68. Найти матрицу билинейной формы , заданной в стандартном базисе, в новом базисе:

а) ,

;

б) ,

;

в) ,

.

61