§2. Квадратичная форма
Если в билинейной форме (х, у) положить у = х, то получим частный случай билинейной формы – квадратичную форму (х, х).
Представив билинейную форму (х, у) в виде суммы симметрической и антисимметрической билинейных форм, получим:
.
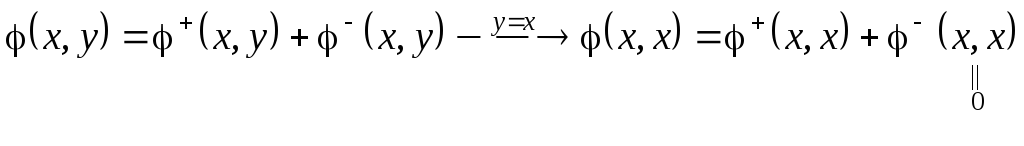Отсюда, ясно, что каждой билинейной форме однозначно ставится в соответствие квадратичная форма (ее матрица симметричная), но не наоборот. Т.е., в общем случае, по имеющейся квадратичной форме нельзя однозначно восстановить билинейную форму, из которой она получена. НО …
2°. Для каждой квадратичной формы существует, и при том только одна, симметричная билинейная форма, из которой получена данная квадратичная форма. (Эта симметричная билинейная форма называется полярной к заданной квадратичной форме).
◀ (х + у, х + у) = (х, х) + (у, х) + (х, у) + (у, у) если (х, у) = (у, х), то
(х+у,
х+у)
= (х,
х)
+ 2(х,
у)
+ (у,
у),
т.е. (х,
у)
=
{(х+у,
х+у)
– (х,
х)
– (у,
у)}.
▶
§3. Классификация квадратичных форм
а) Если rangA = n (А – матрица квадратичной формы, n – размерность пространства V), то форма (х, х) (и форма (х, у)) называется невырожденной.
б) Форма называется положительно (отрицательно) определенной, если х (х, х) > 0 ((х, х) < 0). Такие формы называются знакопостоянными.
в) Если х (х, х) 0 (или (х, х) 0) то, форма (х, х) называется квазизнакопостоянной.
г) Если х 0 и у 0 такое, что (х, х) > 0 и (у, у) < 0, то форма (х, х) называется знакопеременной.
3°. Если форма (х, у) полярная к форме (х, х) и (х, у) положительно определена то (х, у) – задает в V скалярное произведение.
Доказать самостоятельно.
§4. Канонический вид квадратичных форм
Учитывая, что элементы матрицы квадратичной формы aij = (ei, ej) мы можем заключить, что элементы матрица квадратичной формы зависят от выбора базиса.
Если
для формы (х,
х)
в пространстве V
существует базис
в котором матрица(х,
х)
имеет диагональный вид (т.е. aij
= 0 для
i
j),
и следовательно форма (х,
х)
записывается так
то такой базис называется каноническим
базисом(х,
х)
в пространстве V
а запись формы в этом базисе называется
каноническим видом формы.
Постановка задачи: Для формы (х, х) 0 найти базис, в котором форма имеет канонический вид.
Метод Лагранжа (метод выделения полных квадратов) приведения формы к каноническому виду.
Пусть
в некотором базисе
форма имеет вид:
.
1).
Пусть aii
= 0 (i),
но aij
0. Не ограничивая общности можно считать,
что а12
≠ 0. Тогда
и получим
(в записи формы появились члены, содержащие
квадраты координат).
2). aii 0. Допустим, что а12 ≠ 0. Тогда:
.
При
этом:
.
Связь
между координатами ξi
и ηi
позволяет установить векторы нового
базиса
.
Пример:
=
=
=
=
.
При
этом
,
т.е.
.
Векторы нового базиса е1, е2, е3, е3, получаются из старых f1, f2, f3, f4 так:
e1 = f1; e2 = 3f1 + 2f2; e3 = –2f1 + 0,5f3 + 0,5f4; e4 = 0,5f3 – 0,5f4.
Метод Якоби приведения формы к каноническому виду.
Пусть
форма (x,
x)
в базисе
имеет матрицуА,
где aik
= (fi,
fk);
и, при этом, главные миноры матрицы
квадратичной формы отличны от нуля:
10,
20,
30,
…, n
= detA
0
. Форма (x,
x)
в базисе
имеет вид:(x,
x)
=
.
Требуется найти базис {e1,
e2,
…, en},
чтобы (ei,
ek)
= 0 (i
k).
Векторы канонического базиса {e1,
e2,
…, en},
ищем из соотношений:
.
(1)
При этом, нетрудно заметить, что ℒ(е1, е2, …, еn) = ℒ(f1, f2,…, fn). Отметим, что если (ek, fi) = 0, i = 1, 2, …, k –1, то (ei, ek) = 0 i = 1, 2, …, k –1. В счамом деле
(ei, ek) = (ek, i1f1 + i2f2 + … + iifi) = 0.
Тогда коэффициенты ij будем искать из соотношений:
(ek, fi) = 0 (j < k)
(ek, fk) = 1. (*)
Тогда для коэффициентов разложения: ek = k1f1 + k2f2 + k3f3 +…+ knfn из условий (*),
получим систему уравнений :
(ek,f1) = k1 (f1,f1) + k2 (f2,f1) + k3 (f3,f1) + … … … + kk (fk,f1) = 0
(ek,f2) = k1 (f1,f2) + k2 (f2,f2) + k3 (f3,f2) + … … … + kk (fk,f2) = 0
… … … … … … … … … … … … … … … … … … … … … … … …
(ek,fk-1) = k1 (f1,fk-1) + k2 (f2,fk-1) + k3 (f3,fk-1) + … … + kk (fk,fk-1) = 0
(ek,fk) = k1 (f1,fk) + k2 (f2,fk) + k3 (f3,fk) + … … … … + kk (fk,fk) = 1
Полученная система линейных уравнений имеет единственное решение, ибо ее определитель Δk 0. При этом получим, что: (ek, ei) = 0 (k i), и (ek, ek) 0.
Запишем:
(ek,ek) = k1 (ek,f1) + k2 (ek,f2) + k3 (ek,f3) + … + kk-1 (ek,fk-1) + kk (ek,fk) = kk.
Найти kk можем из системы уравнений, которая записана выше, по правилу Крамера:
kk
=
.
Таким образом, форма (x,
x)
в базисе
имеет канонический вид:
(x,
x)
=
,
где11=
,
22=
,
33=
,
…, nn=
.
Здесь 0
= 1.
Пример приведения квадратичной формы к каноническому виду методом Якоби.
Пусть
форма:
задана в базисеf1(2,
0, 0), f2(0,
1, 0), f3(0,
0, 1), а полярная ей билинейная форма
имеет вид:
.
Матрица
билинейной формы и соответствующей ей
квадратичной формы равна:
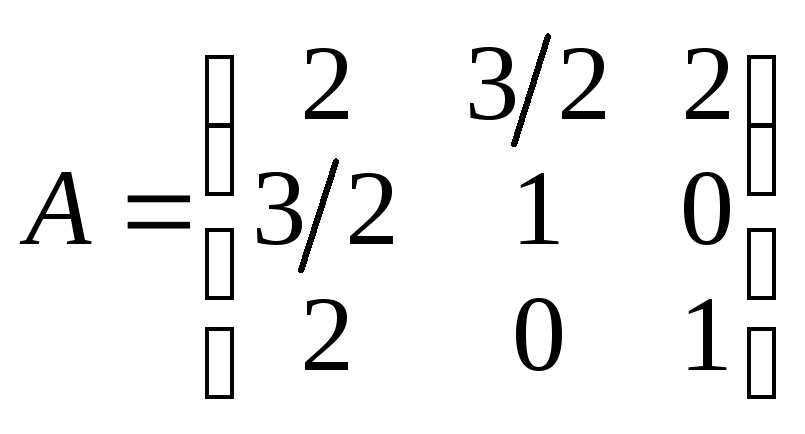и
ее главные миноры:1
= 2; 2
= –14;
3
= –174.
Векторы е1,
е2,
е3
ищем в виде:
e1 = 11f1 = ( 11,0,0 ), e2 = 21f1 + 22f2 = (21, 22, 0), e3 = 31f1 + 32f2 + 33f = (31, 32, 33).
Получаем:
а)
(e1,
f1)
= 1
211
= 1
11
=
e1
;
б)
е2(6,
–8, 0);
в)
.
Получены векторы канонического базиса:
e1
=
f1;
е2(6,
–8, 0) = 6f1
– 8f2;
=
(8f1
–12f2
+ f3)
и в этом базисе форма (х, х) имеет канонический вид:
.