3. Метод представления определителя в виде суммы определителей.

Вычислить определитель:.

Заметив, что элементы первого столбца представлены как суммы двух чисел, разложим определитель в сумму двух определителей:

.

Теперь каждый из полученных определителей разложим в сумму двух определителей, воспользовавшись тем, что элементы вторых столбцов у них также представлены в виде сумм, и т.д. Проделав это, получим (n > 2), что строки полученных определителей будут такими: a_i, a_i, … _, a_i или b_1, b_2, … _,b_n . Строки 1^го типа пропорциональны, 2^го типа равны и, следовательно, все слагаемые равны нулю. Следовательно: D_n = 0 (n > 2).

Для определителей такого же типа, но первого и второго порядков получим:

D₁ = | a₁+ b₁ | = a₁+ b₁; D₂ = =

= a₁b₂ – a₂b₂ + b₁a₂ – a₁b₁ = (a₁ – a₂)b₂ + (a₂ + a₁)b₁ = (a₁ – a₂)(b₂ – b₁).

Метод рекуррентных (возвратных) соотношений.

Вычислить определитель n–го порядка: .

Разлагая определитель по элементам первой строки, получим рекурентное соотношение: D_n=.

Разложив определитель в правой части соотношения по первому столбцу, запишем новое рекурентное соотношение: D_n = 5D_n–1 – 6D_n–2.

Представляя это соотношение в виде: D_n – 2D_n–1 = 3(D_n–1 – 2D_n–2) и вводя обозначение:

Т_n = D_n – 2D_n–1 получим: Т_n = 3Т_n–1 – 3²Т_n–2 = … =3 ^n-2T₂=3ⁿ.

Аналогично, записав рекурентное соотношение в виде: D_n – 3D_n–1 = 2(D_n–1 – 3D_n–2) и обозначая: V_n = D_n – 3D_n–1 получим V_n = 2V_n=1 = 2²V_n–2=…= 2ⁿ .

т

.е.D_n = 3^{n + 1} – 2^{n + 1}.

В общем случае, для рекуррентных соотношений типа: D_n = pD_{n – 1} + qD_{n – 2 .}можно проделать следующее: пусть  и  корни уравнения x² – px – q = 0, т.е. p =  + ,

q = –. Тогда D_n = D_{n – 1} + D_{n –1} – D_{n – 2}^; D_n – D_{n -–1} = (D_{n – 1} – D_{n – 2}), т.е. S_{n =} S_{n – 1} или D_n – D_{n -–1} = (D_{n – 1} – D_{n – 2}), т.е. V_{n =} V_{n – 1} .

Аналогично можно поступить и в более сложных рекуррентных соотношениях.

5. Метод изменения элементов определителя.

19. Если ко всем элементам определителя D добавить одно и то же число x, то определитель увеличится на произведение числа x на сумму алгебраических дополнений всех элементов определителя D.

◀ Пусть D = | a_ij |; D = | a_ij + x |. Разложим D в сумму двух определителей относительно первой строки, каждый из них на два относительно второй строки и т.д. Слагаемые, содержащие более одной строки элементов x, равны нулю.

Слагаемые, содержащие одну строку элементов x, разложим по этой строке. Получим D = D + x. ▶

а). . Вычтем из всех элементов определителя числоx

. Тогда D_n = (a₁ – x)(a₂ – x)…(a_n – x) + x= (a₁ – x)(a₂ – x)...

…(a_n – x) + x = (a₁ – x) (a₂ – x) … (a_n – x) + x= (a₁ – x )( a₂ – x )…( a_n– x ) +

+ x =

= x(a₁ – x) (a₂ – x) … (a_n – x) .

Раздел 5. СистемЫ линейных уравнений

§ 1. Постановка задачи и терминология

Требуется найти x₁, x₂ … x_n удовлетворяющие следующим соотношениям:

.

Здесь a_ijR (i = 1, 2, … , m; j = 1, 2,… , n) и b_iR (i =1, 2,… , m) – заданные числа.

Введем обозначения: 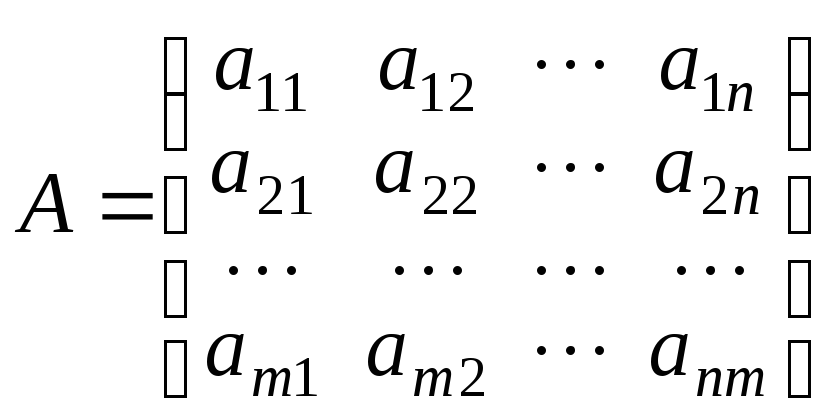– главная матрица системы уравнений;

–вектор-столбец неизвестных; – вектор-столбец правых частей.

При таких обозначениях система может быть записана в матричной форме: Ax = b.

Вектор называется решением системы Ax = b, если Ac  b.

Если b₁ = b₂ = … = b_m= 0, то система уравнений называется однородной.

.

Если хотя бы одно из значений b_i (i = 1, …, m) отлично от нуля система уравнений называется неоднородной.

Матрица 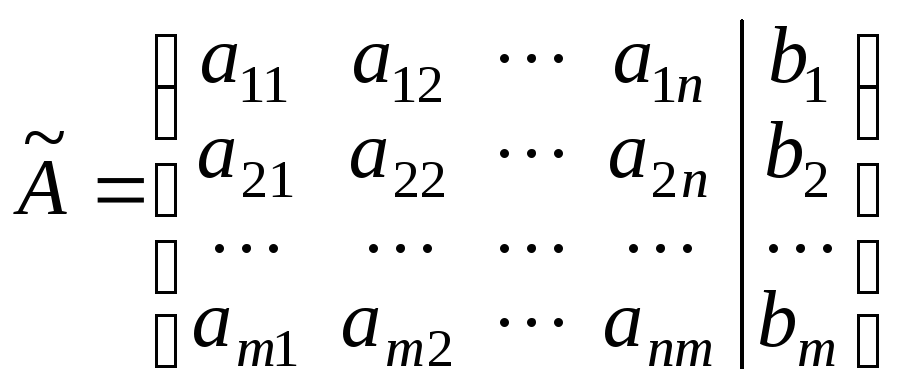называется расширенной матрицей системы уравнений.

Если система линейных уравнений имеет хотя бы одно решение, то она называется совместной. Если система линейных уравнений имеет единственное решение, то она называется определенной.

Вопросы, на которые нам предстоит ответить по отношению к системе линейных уравнений:

А. Совместна ли система, т.е. имеет ли она хотя бы одно решение?

В. При положительном ответе на предыдущий вопрос определена ли система, т.е. будет ли ее решение единственным?

С. Как находить решение системы?

В случае однородной системы на вопрос А, можно ответить сразу:

Однородная система уравнений всегда совместна. Набор x₁ = x₂ = … = x_n = 0 является решением системы. Такое решение называется тривиальным решением. Поэтому для однородной системы линейных уравнений вопрос В звучит следующим образом:

Имеет ли система линейных однородных уравнений другие решения, кроме тривиальных?