§8. Пример вычисления определителя

Вычислить определитель 5^го порядка:

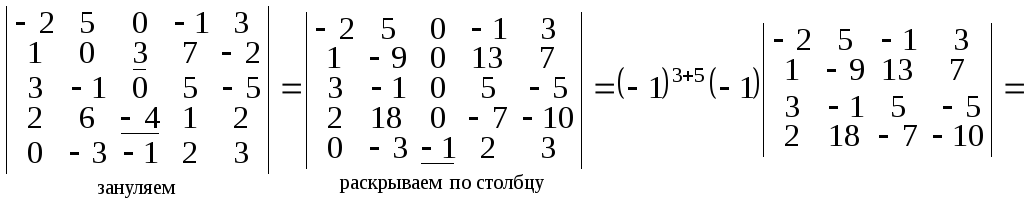
–24(104 – 61) = –2443 = –1032.

§9. Теорема Лапласа

Пусть задана квадратная матрица A_nn. Выберем в матрице A k-строк i₁, i₂, …, i_k и k-столбцов j_1, j_2, ... j_k. Определитель матрицы образованной элементами, стоящими на пересечении выбранных столбцов и строк называется минором k^го порядка и обозначается _. Если из матрицы А вычеркнуть выбранные строки и столбцы то определитель оставшейся матрицы называется минором дополнительным к минору и обозначается .

Величина называется алгебраическим дополнением к минору и обозначается .

18. Теорема Лапласа.

detA = .

Суммирование здесь производится по всем минорам k^го порядка, стоящим в выбранных k-строках или в выбранных k–столбцах. ◀ ▶

Пример. Вычислить следующий определитель раскрывая его по минорам второго порядка, стоящим во второй и третьей строках определителя:

Существует шесть различных миноров второго порядка, стоящих в указанных строках:

M₁₂= ; M₁₃= ; M₁₄= ; M₂₃= ; M₂₄= ; M₃₄= .

Дополнительные к ним миноры:

; ; ; ; ; .

Найдем соответствующие алгебраические дополнения:

A₁₂ = (-1)^2+3+3+4 M₃₄ = M₃₄; A₁₃ = (-1)^2+3+2+4 M₂₄ = -M₂₄; A₁₄ = (-1)^2+3+2+3 M₂₃ = M₂₃; A₂₃ = (-1)^2+3+1+4 M₁₄ = M₁₄; A₂₄ = (-1)^2+3+1+3 M₁₃ = -M₁₃; A₃₄ = (-1)^2+3+1+2 M₁₂ = M₁₂.

Теперь, используя теорему Лапласа, можно записать:

 = M₁₂A₁₂ + M₁₃A₁₃ + M₁₄A₁₄ + M₂₃A₂₃ + M₂₄A₂₄ + M₃₄A₃₄ = M₁₂M₃₄ - M₁₃M₂₄ + M₁₄M₂₃ + + M₂₃M₁₄ - M₂₄M₁₃ + M₃₄M₁₂ = 2 ( M₁₂M₃₄ - M₁₃M₂₄ + M₁₄M₂₃ ) = 2 (-1354+1245-911) = –522.

§10. Некоторые приемы вычисления определителей nГо порядка

1. Метод приведения к треугольному виду.

а) Вычислить определитель: .

Вычитая первую строку из всех остальных, получаем определитель, который имеет треугольный вид и, следовательно, равен произведению диагональных элементов:

. В итоге D_n = (–1)^n–1.

б) Вычислить определитель:.

Вычитаем первую строку из всех остальных, а затем, из столбцов определителя выносим: из первого а₁ – х; из второго а₂ – х; …..; из n ^го а_n – х. Получим:

D = (a₁ – x) (a₂ – x)… (a_n – x).

Запишем первый элемент первого столбца в виде: = 1 +, и все столбцы полученного определителя прибавим к первому столбцу. Получим определитель треугольного вида, который равен произведению диагональных элементов. Следовательно:

D = (a₁– x) (a₂ – x)…(a_n – x)x+++ … +.

2. Метод выделения линейных множителей.

а) Вычислить определитель .

1. Прибавляя к первому столбцу определителя остальные три, обнаружим, что в первом столбце есть общий множитель, который равен х + у + z. Следовательно, определитель делится на х + у + z.

2. Аналогично, прибавляя к первому столбцу второй и вычитая из него третий и четвертый столбцы, получаем, что определитель делится на х – у – z.

3. Если первый столбец сложить с третьим и вычесть второй и четвертый, то получим, что определитель делится на х – у + z.

4. Если к первому столбцу прибавить четвертый и вычесть второй и третий столбцы, то обнаружим, что определитель имеет множитель х – у + z. Итак:

= .

Ясно, что определитель является многочленом 4^й степени по x, по y и по z. Справа тоже многочлен той же степени. Поэтому V = const. В определитель x⁴ входит в слагаемом:

a₁₂a₂₁a₃₄a₄₃ = (–1)²хххх = х⁴.

В правой части старший член по х: Vx⁴, т.е. V = 1. Получаем результат:

= (x + y + z)(x – y – z)(x – y + z)(x + y – z) = x⁴ + y⁴ + z⁴ – 2x²y² – 2x²z² – 2у²z².

б) Вычислить определитель n-го порядка: .

Этот определитель называется определителем Вандермонда. Рассматривая его как многочлен (n –1)^й степени относительно x_n увидим, что он обращается в 0 при x_n = x_1, x_n = x_2, … x_n = x_{n – 1}. Тогда D_n = a_{n – 1}(x_n – x₁)(x_n – x₂) … (x_n – x_n–1), причем a_n–1 = = D_n–1. Повторяя эту процедуру, получим: D_n = (x₂ – x₁)(x₃ – x₂)(x₃ – x₁)(x₄ – x₃)(x₄ – x₂)(x₄ – –x₁)… = .