
Алгебра / Короткие_Вопросы_2
.doc-
Дайте визначення оператора, який діє з
 в
в
 .
. -
Дайте визначення лінійного оператора.
-
Що називають нульовим оператором?
-
Що називають одиничним оператором?
-
Що називають оператором подібності?
-
Що називають оператором диференціювання?
-
Які два лінійні оператори називаються рівними?
-
Дайте визначення суми двох лінійних операторів.
-
Дайте визначення операції множення лінійного оператора на число.
-
Визначте лінійний простір лінійних операторів, які задано на
 (внутрішня та зовнішня операції,
нейтральний елемент, протилежний
елемент).
(внутрішня та зовнішня операції,
нейтральний елемент, протилежний
елемент). -
Дайте визначення операції множення двох лінійних операторів.
-
Як можна задати другу внутрішню операцію на лінійному просторі лінійних операторів?
-
Як вводиться поняття матриці лінійного оператора?
-
Запишіть формулу, яка визначає елементи матриці лінійного оператора.
-
Взаємнооднозначне співвідношення між лінійними операторами та квадратними матрицями можна ввести: а) незалежно від вибору базису; б) у заданому базисі; в) тільки в ортонормованому базисі.
-
Опишіть метод побудови матриці лінійного оператора у заданому базисі.
-
Дайте визначення образа лінійного оператора.
-
Як позначається образ лінійного оператора?
-
Дайте визначення ядра лінійного оператора.
-
Як позначається ядро лінійного оператора?
-
Як визначити розмірність образа лінійного оператора, коли лінійний оператор задано матрицею?
-
Як визначити розмірність ядра лінійного оператора, коли лінійний оператор задано матрицею?
-
Нехай

лінійний простір, в якому діє лінійний
оператор А. Яка з наступних формул є
найбільш коректною: а)
лінійний простір, в якому діє лінійний
оператор А. Яка з наступних формул є
найбільш коректною: а)
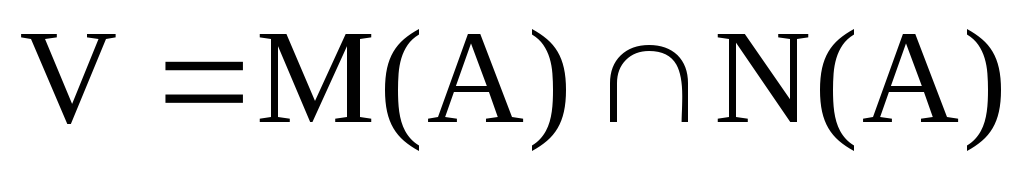 ;
б)
;
б)
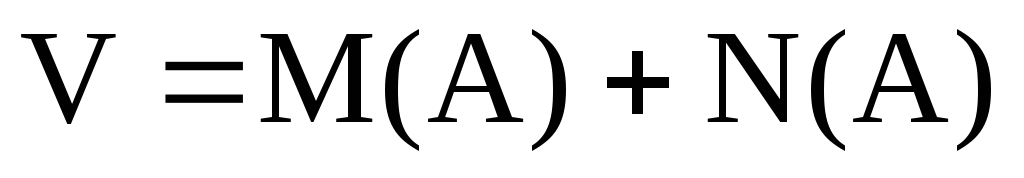 ;
в)
;
в)
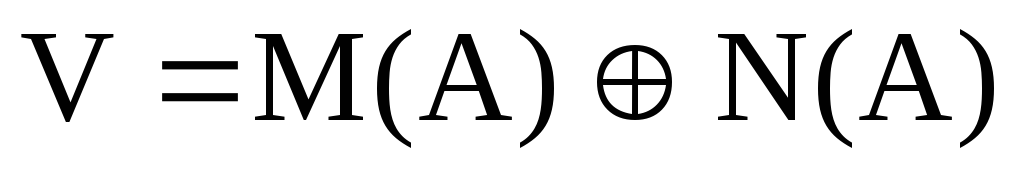 ?
? -
Що називають дефектом лінійного оператора?
-
Дайте визначення невиродженого лінійного оператора.
-
Чому дорівнює ядро невиродженого лінійного оператора?
-
Як визначити розмірність образа невиродженого лінійного оператора, який задано квадратною матрицею?
-
Доведіть, що при дії лінійного оператора з
 в
в
 нейтральний елемент з
нейтральний елемент з
 відображається в нейтральний елемент
з
відображається в нейтральний елемент
з
 .
. -
Якщо лінійний оператор А є невиродженим, то що можна сказати про визначник матриці лінійного оператора?
-
За якої умови лінійний оператор А має обернений?
-
Якщо лінійний оператор А має обернений, то що можна сказати про визначник матриці лінійного оператора?
-
Чому дорівнює дефект невиродженого оператора?
-
Доведіть, що невироджений лінійний оператор, що діє з
 в
в
 ,
встановлює взаємнооднозначне
співвідношення між векторами
,
встановлює взаємнооднозначне
співвідношення між векторами
 та
та
 .
. -
Невироджений лінійний оператор переводить лінійно незалежні вектори в: а) лінійно залежні вектори; б) лінійно незалежні вектори; в) ортогональні вектори.
-
Дайте визначення лінійного підпростору, інваріантного до лінійного оператора.
-
Відносно яких двох лінійних операторів є інваріантними будь- які лінійні підпростори лінійного простору, в якому ці оператори діють?
-
Які два лінійні підпростори довільного лінійного простору є інваріантними відносно будь- яких операторів, що діють в цьому просторі?
-
Якщо лінійний підпростір
 є інваріантним відносно лінійного
оператора А (
є інваріантним відносно лінійного
оператора А ( ),
то: а)
),
то: а)
 не є інваріантним підпростором оберненого
лінійного оператора
не є інваріантним підпростором оберненого
лінійного оператора
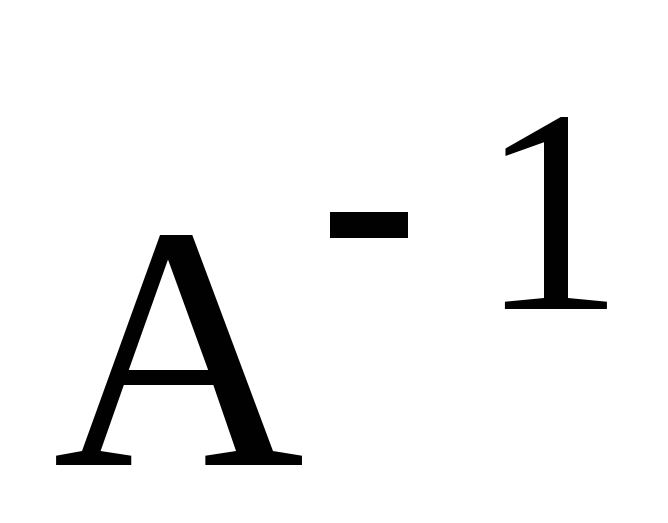 ;
б)
;
б)
 є інваріантним підпростором оберненого
лінійного оператора
є інваріантним підпростором оберненого
лінійного оператора
 ;
в)
;
в)
 є інваріантним підпростором оберненого
лінійного оператора
є інваріантним підпростором оберненого
лінійного оператора
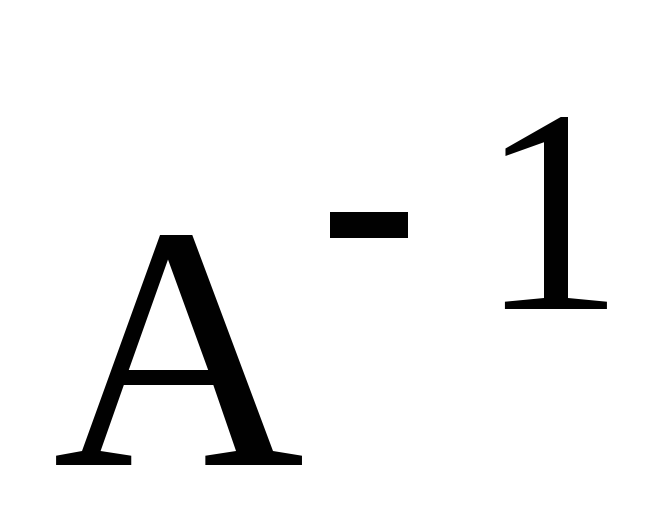 ,
якщо
,
якщо
 .
. -
Дайте визначення власного вектора лінійного оператора.
-
Чи може власний вектор лінійного оператора бути нейтральним елементом?
-
Дайте визначення власного значення лінійного оператора.
-
Чи може власне значення лінійного оператора дорівнювати 0?
-
Нехай

одновимірний інваріантний підпростір
лінійного оператора А, тоді: а) серед
векторів
одновимірний інваріантний підпростір
лінійного оператора А, тоді: а) серед
векторів
 існує один власний вектор лінійного
оператора А; б) серед векторів
існує один власний вектор лінійного
оператора А; б) серед векторів
 не існує власних векторів лінійного
оператора А; в) усі вектори
не існує власних векторів лінійного
оператора А; в) усі вектори
 (окрім
(окрім
 )
є власними векторами лінійного оператора
А.
)
є власними векторами лінійного оператора
А. -
Нехай

власний вектор лінійного оператора А,
тоді: а) усі вектори лінійної оболонки
власний вектор лінійного оператора А,
тоді: а) усі вектори лінійної оболонки
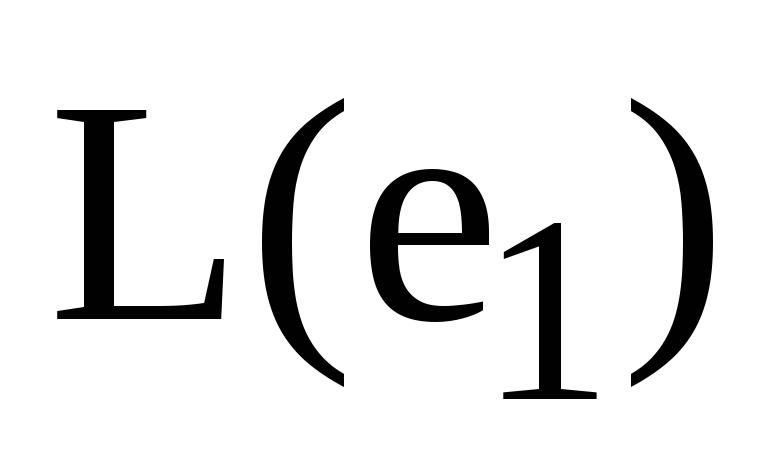 є власними векторами лінійного оператора
А, але їм відповідають різні власні
значення; б) усі вектори лінійної
оболонки
є власними векторами лінійного оператора
А, але їм відповідають різні власні
значення; б) усі вектори лінійної
оболонки
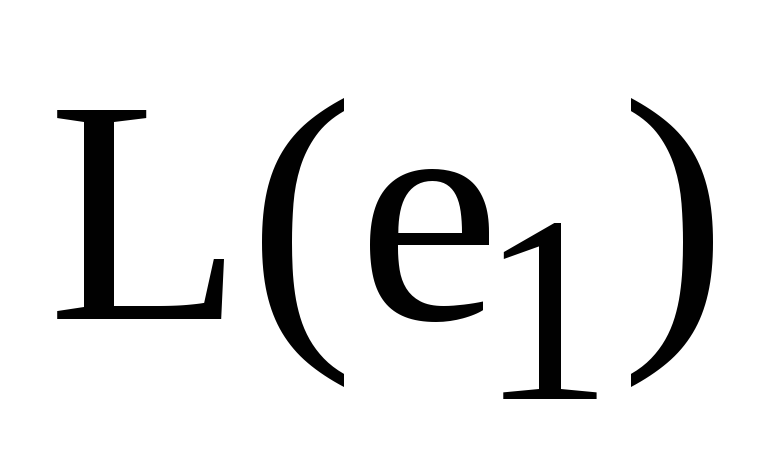 (окрім власне
(окрім власне
 )
не є власними векторами лінійного
оператора А; в) усі вектори лінійної
оболонки
)
не є власними векторами лінійного
оператора А; в) усі вектори лінійної
оболонки
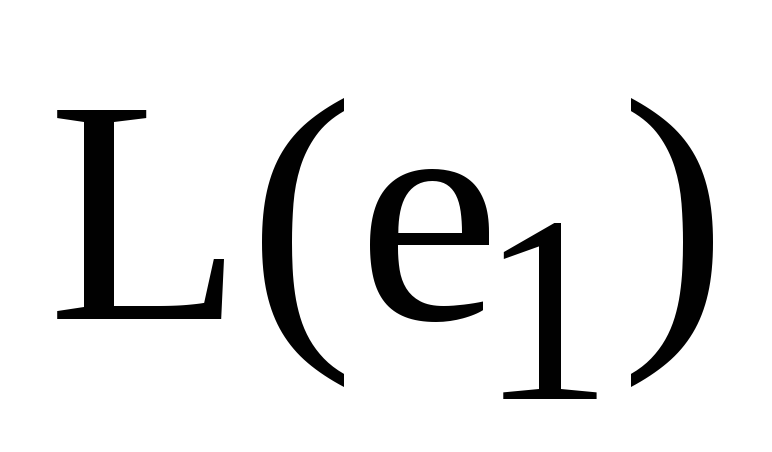 (окрім
(окрім
 )
є власними векторами лінійного оператора
А і при цьому їм відповідає одне власне
значення.
)
є власними векторами лінійного оператора
А і при цьому їм відповідає одне власне
значення. -
Опишіть метод знаходження власних векторів та власних значень лінійного оператора.
-
Дайте визначення характеристичного многочлена лінійного оператора А.
-
Як знайти власні значення лінійного оператора?
-
Як знайти власні вектори лінійного оператора?
-
Знайдіть власні вектори та власні значення лінійного оператора, заданого матрицею
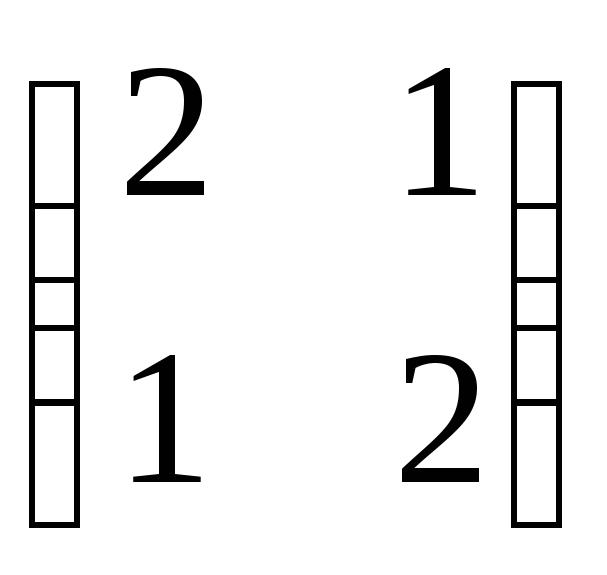 .
. -
Знайдіть власні вектори та власні значення лінійного оператора, заданого матрицею
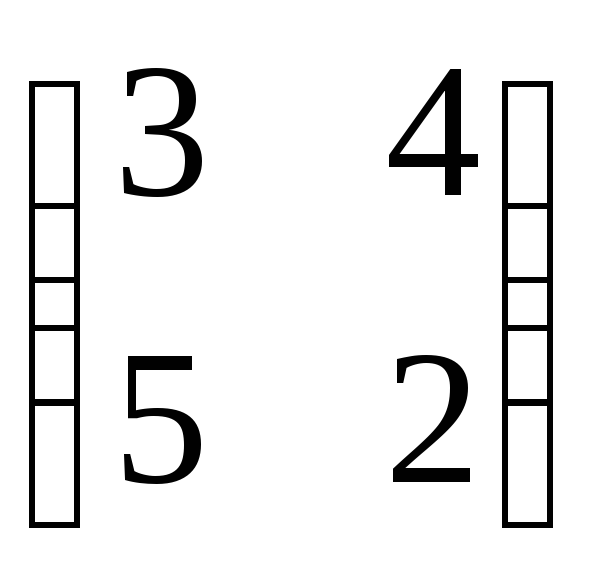 .
. -
Знайдіть власні вектори та власні значення лінійного оператора, заданого матрицею
 .
. -
Який вигляд має матриця лінійного оператора у базисі власних векторів?
-
Власні вектори лінійного оператора, які відповідають різним власним значенням є: а) лінійно залежними; б) лінійно незалежними; в) пропорційними один одному.
-
Дайте визначення спектру лінійного оператора.
-
Дайте визначення сліду матриці.
-
Для всякого лінійного оператора А у дійсному лінійному просторі розмірності n>2 існує: а) тільки один одновимірний інваріантний лінійний простір; б) тільки один двовимірний інваріантний лінійний простір; в) одновимірний або двовимірний інваріантний лінійний простір.
-
Якщо
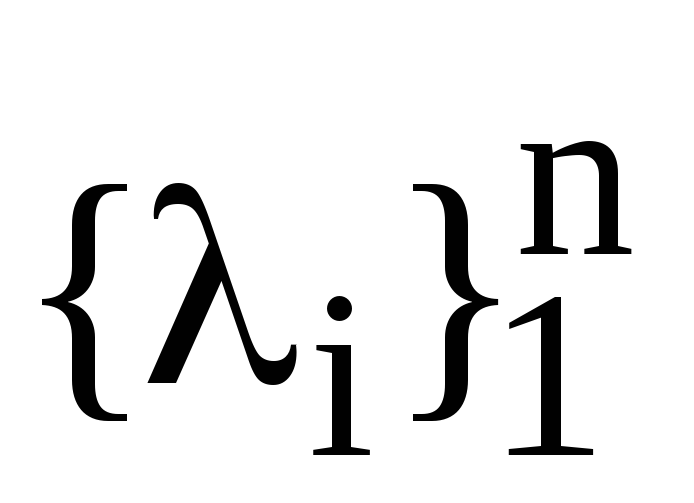
власні значення лінійного оператора
А, то чому дорівнюють власні значення
оберненого лінійного оператора
власні значення лінійного оператора
А, то чому дорівнюють власні значення
оберненого лінійного оператора
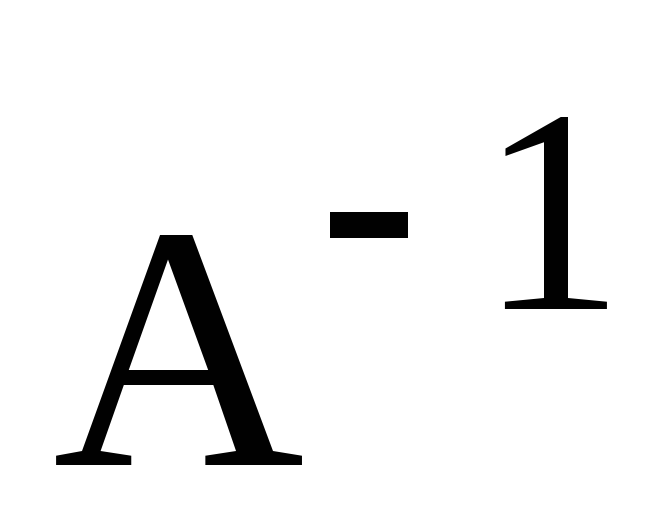 за умови його існування?
за умови його існування? -
Сформулюйте правило побудови матриці переходу з базису
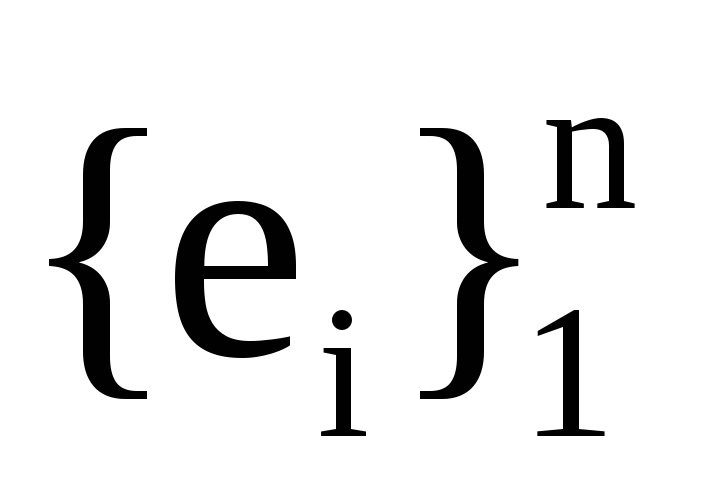 до
базису
до
базису
 .
. -
Якщо
 ―
елементи матриці переходу з базису
―
елементи матриці переходу з базису
 до
базису
до
базису
 ,
то базисні вектори пов’язані формулою:
а)
,
то базисні вектори пов’язані формулою:
а)
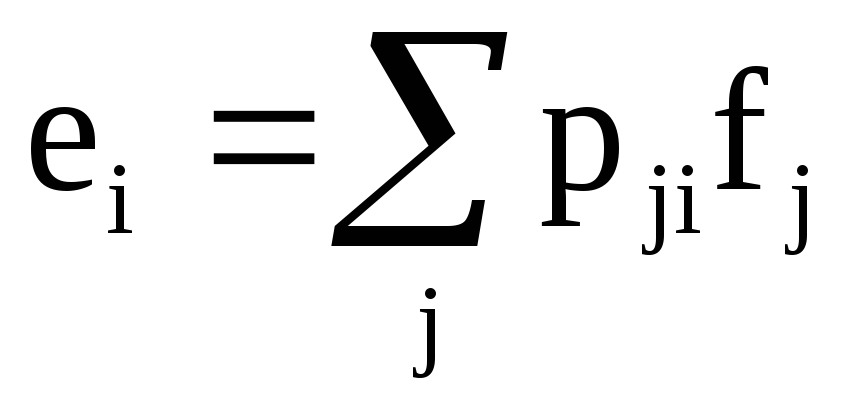 ;
б)
;
б)
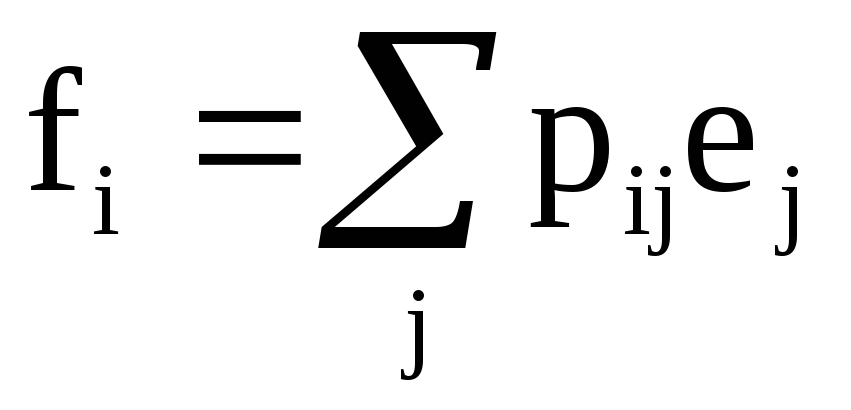 ;
в)
;
в)
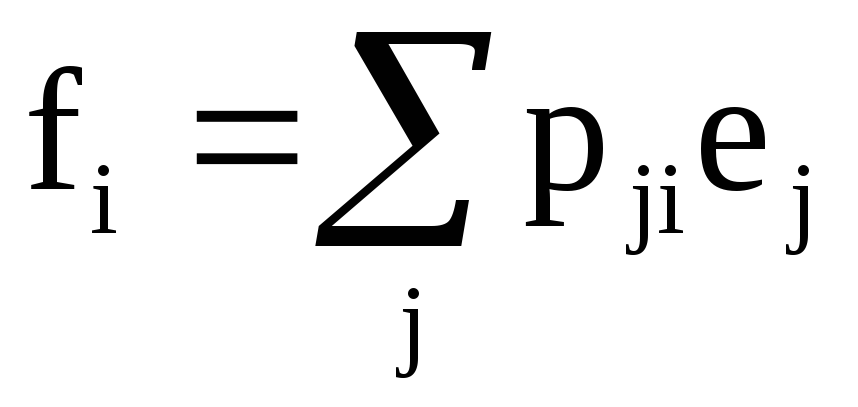 ;
г)
;
г)
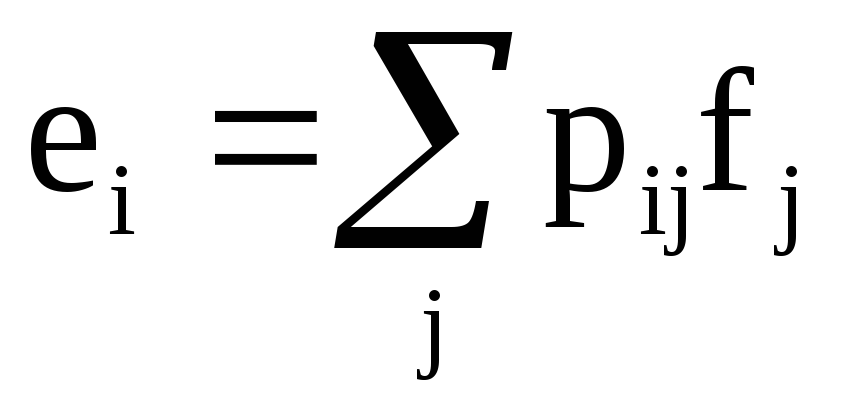 .
. -
Якщо хе― координати вектора х у базисі
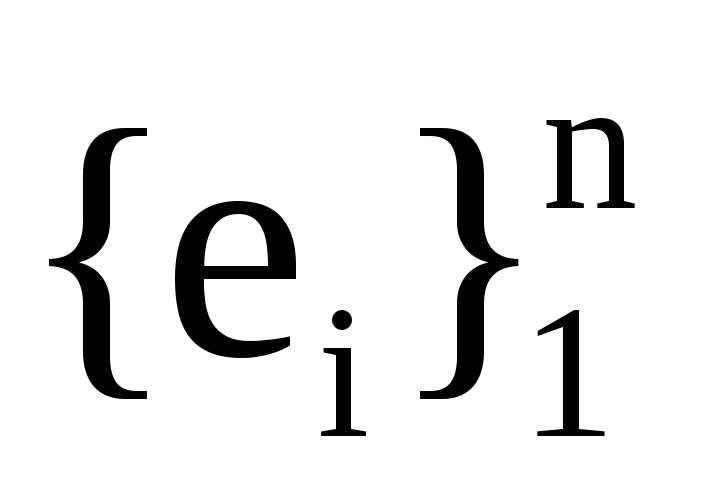 ,
хf―
координати вектора х у базисі
,
хf―
координати вектора х у базисі
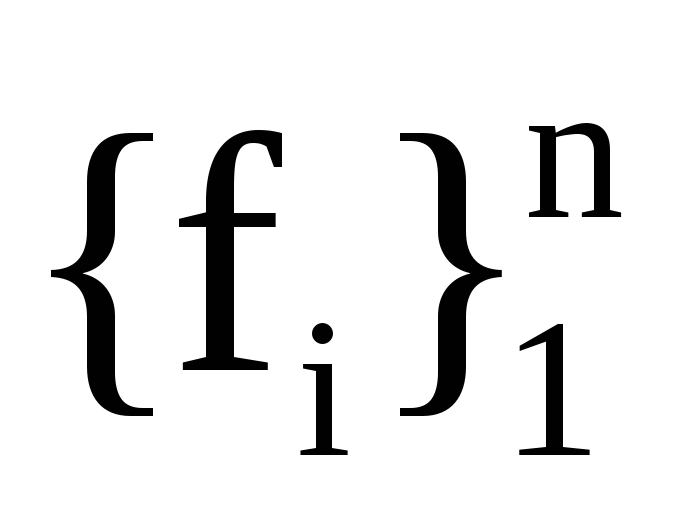 ,
а Р― матриця переходу з базису
,
а Р― матриця переходу з базису
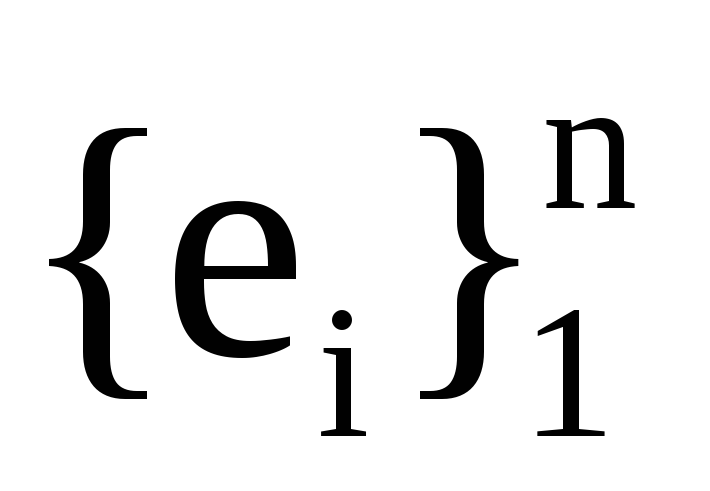 до базису
до базису
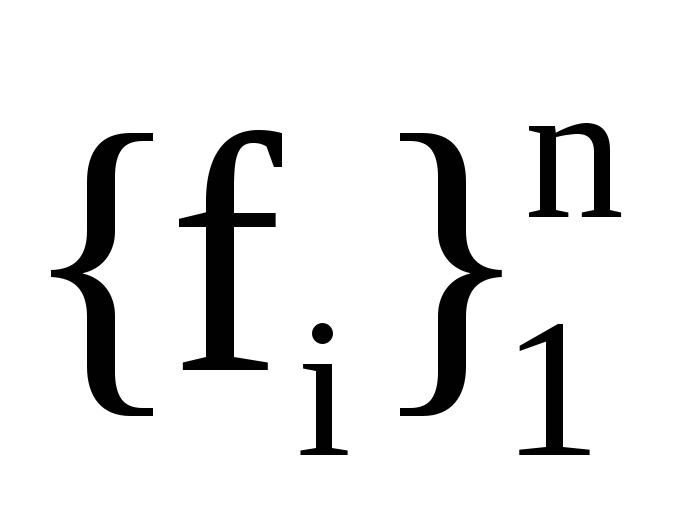 ,
то
виконується
співвідношення: а)
,
то
виконується
співвідношення: а)
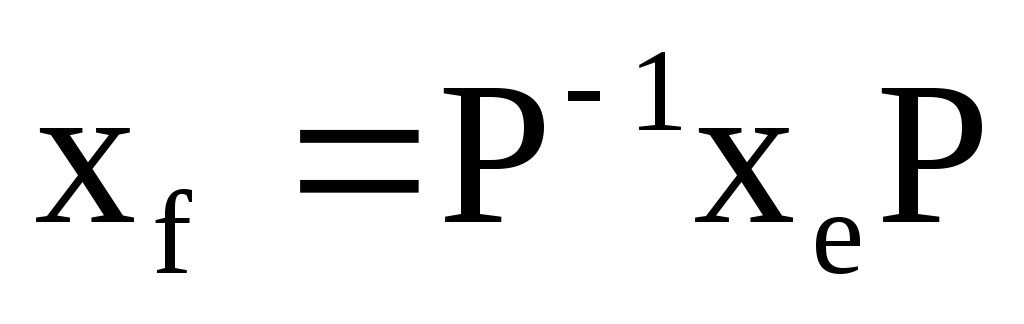 ;
б)
;
б)
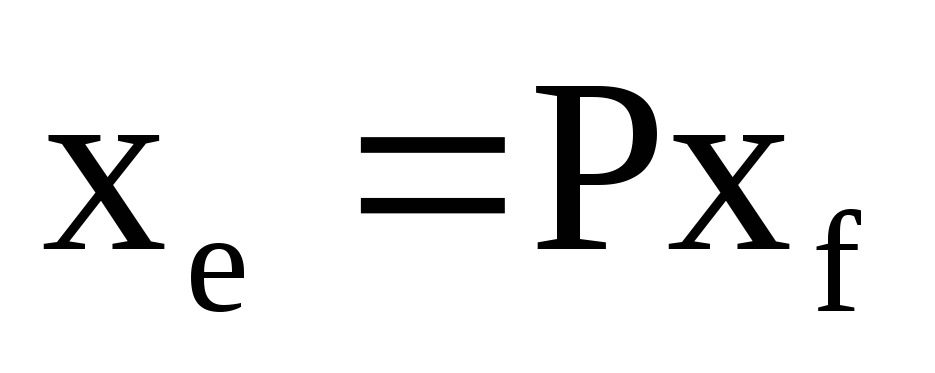 ;
в)
;
в)
 ;
г)
;
г)
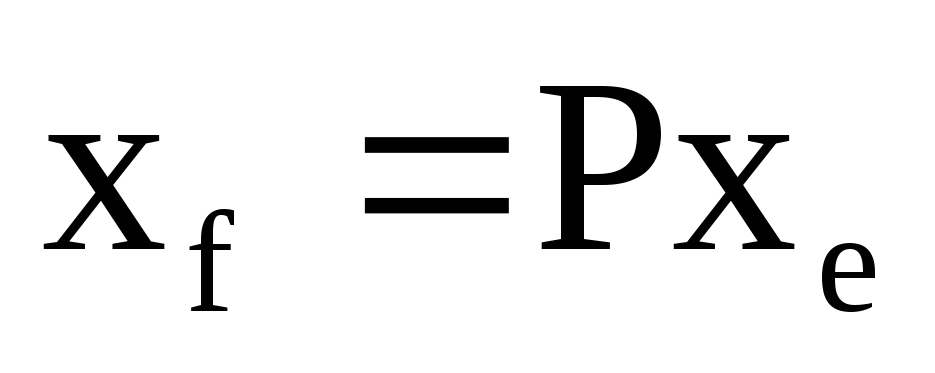 .
. -
Якщо Ае― матриця лінійного оператора у базисі
 ,
Аf―
матриця лінійного оператора у базисі
,
Аf―
матриця лінійного оператора у базисі
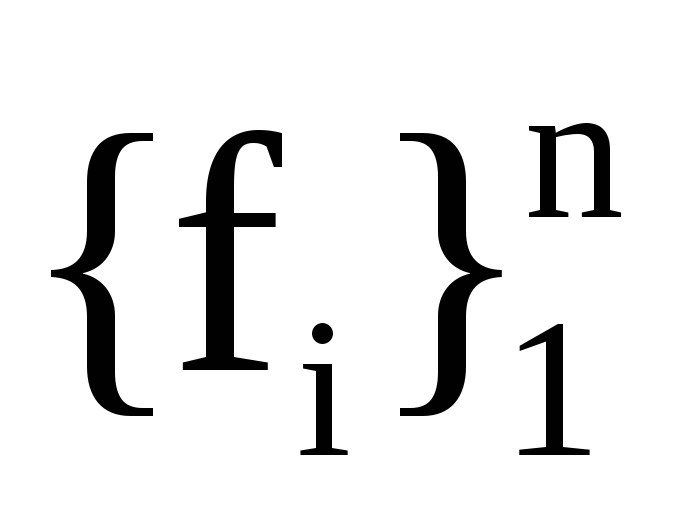 ,
а
Р― матриця переходу з базису
,
а
Р― матриця переходу з базису
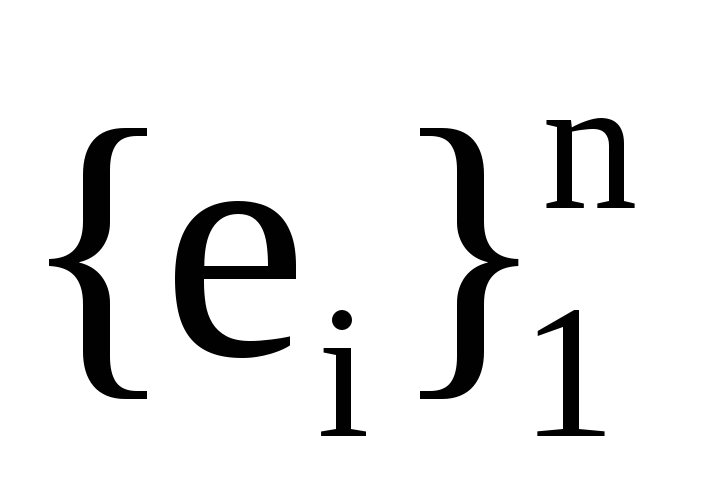 до базису
до базису
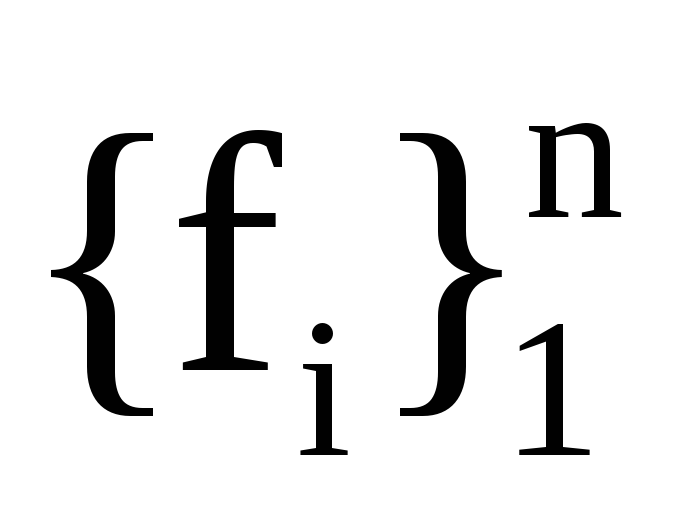 ,
то
виконується
співвідношення: а)
,
то
виконується
співвідношення: а)
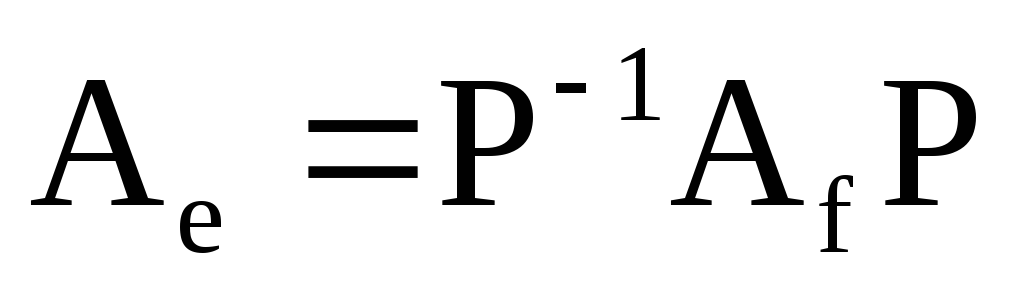 ;
б)
;
б)
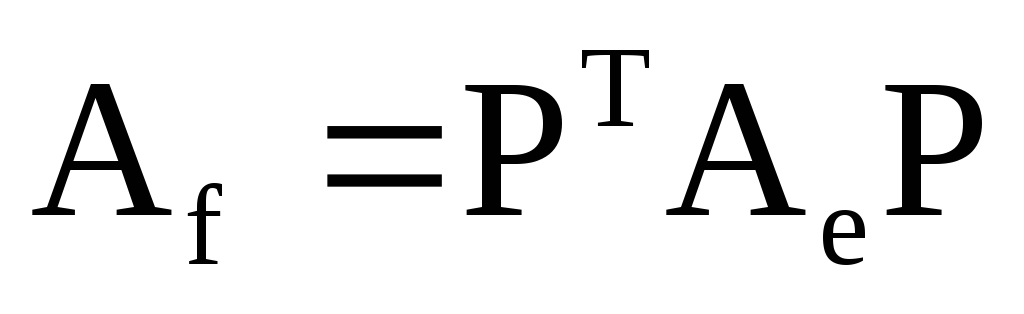 ;
в)
;
в)
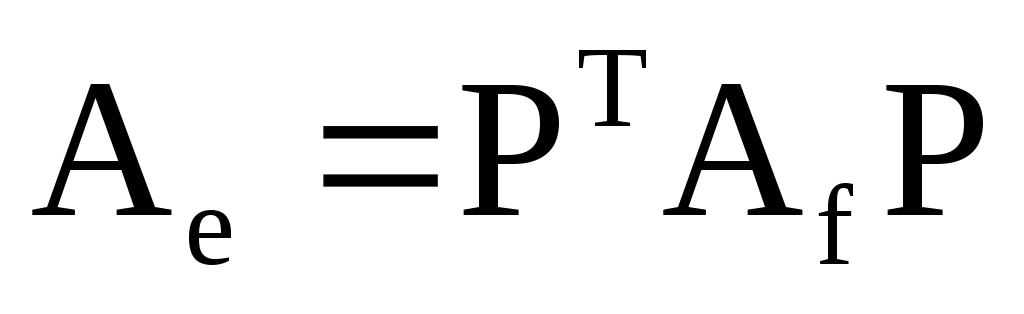 ;
г)
;
г)
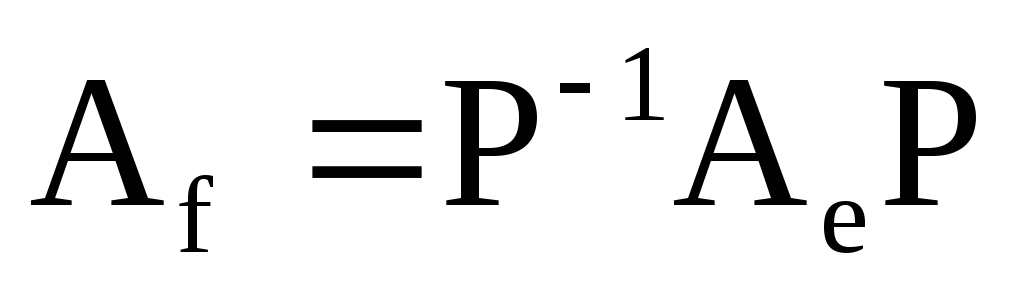 .
. -
Якщо hе― коефіцієнти лінійної форми у базисі
 ,
hf―
коефіцієнти лінійної форми у базисі
,
hf―
коефіцієнти лінійної форми у базисі
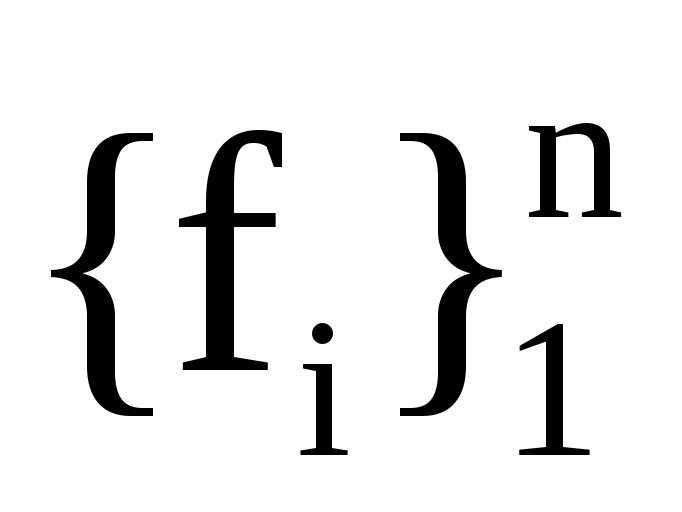 ,
а Р― матриця переходу з базису
,
а Р― матриця переходу з базису
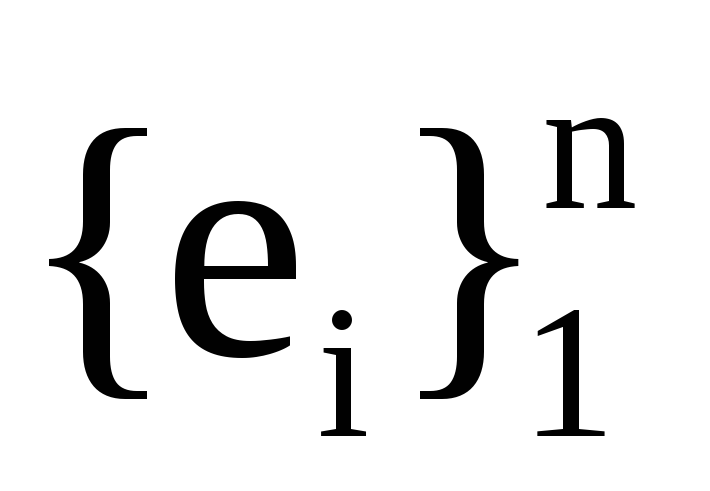 до базису
до базису
 ,
то виконується співвідношення: а)
,
то виконується співвідношення: а)
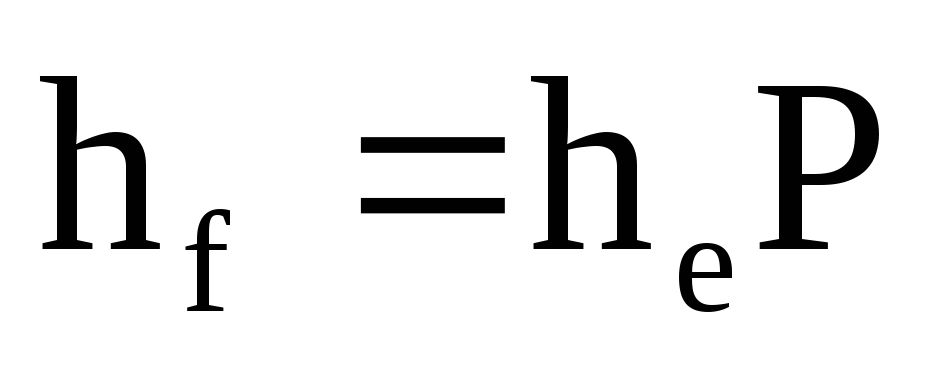 ;
б)
;
б)
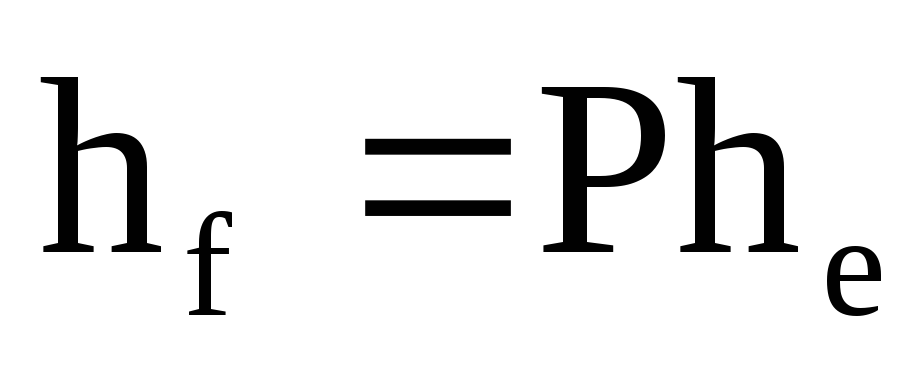 ;
в)
;
в)
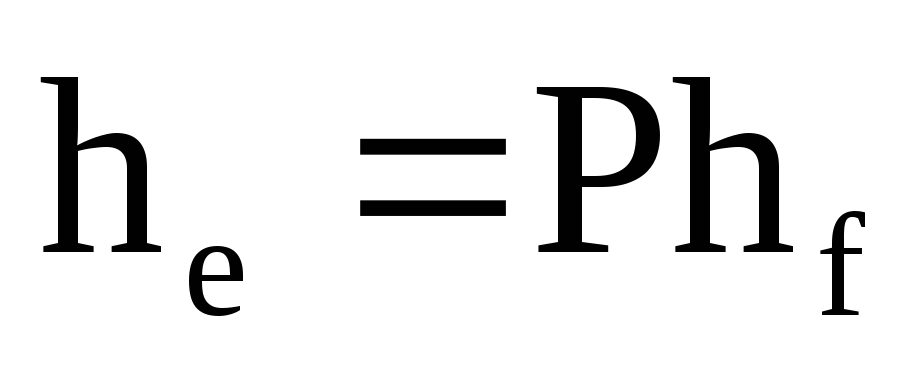 ;
г)
;
г)
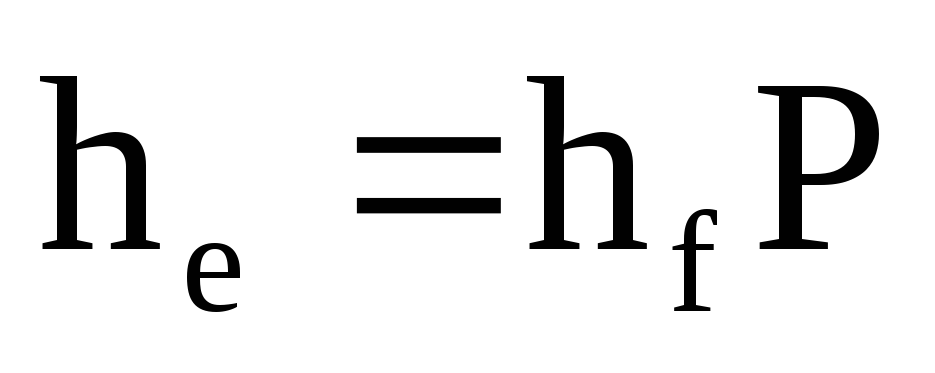 .
. -
Якщо Ве― матриця білінійної форми у базисі
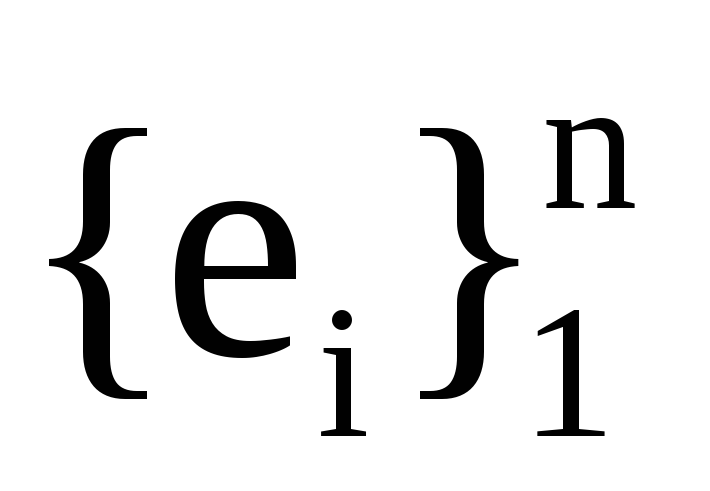 ,
Вf―
матриця білінійної форми у базисі
,
Вf―
матриця білінійної форми у базисі
 ,
а Р― матриця переходу з базису
,
а Р― матриця переходу з базису
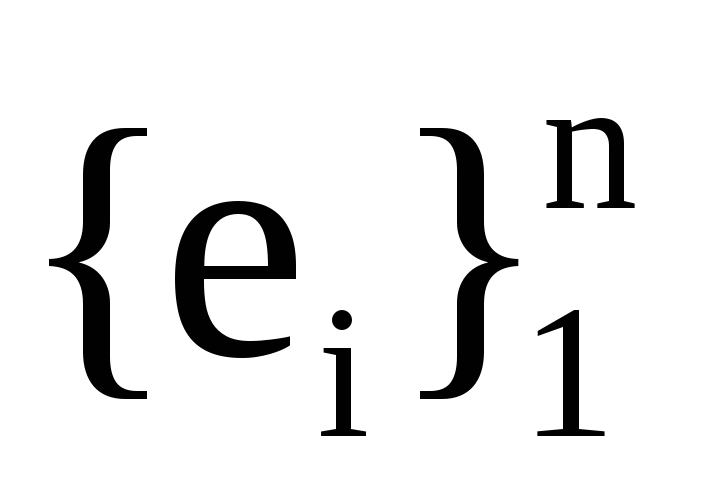 до базису
до базису
 ,
то виконується співвідношення: а)
,
то виконується співвідношення: а)
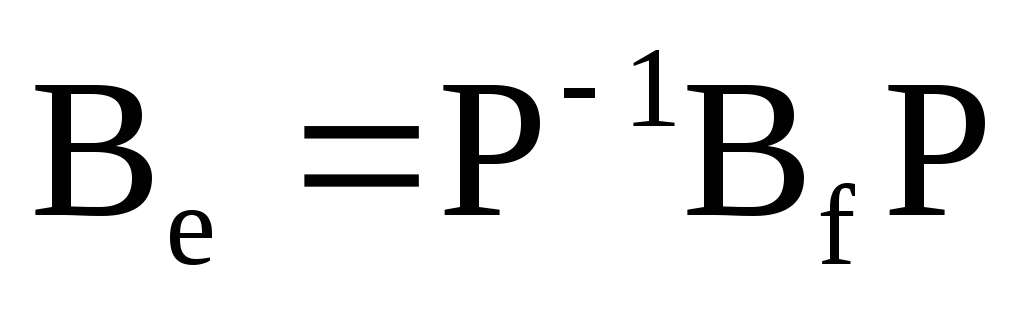 ;
б)
;
б)
 ;
в)
;
в)
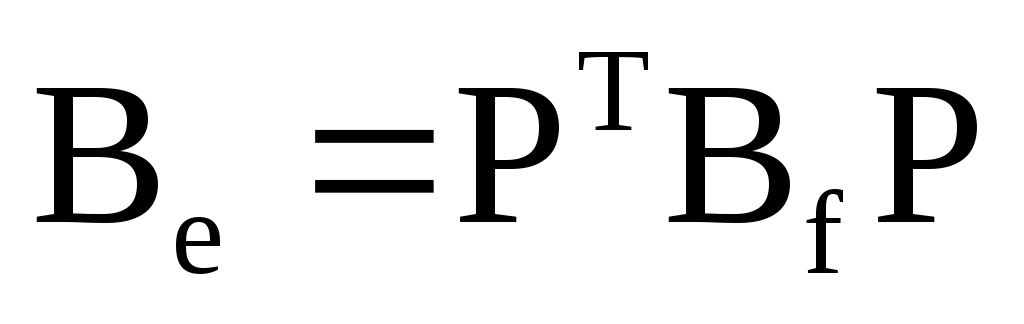 ;
г)
;
г)
 .
. -
Нехай Р― матриця переходу з базису
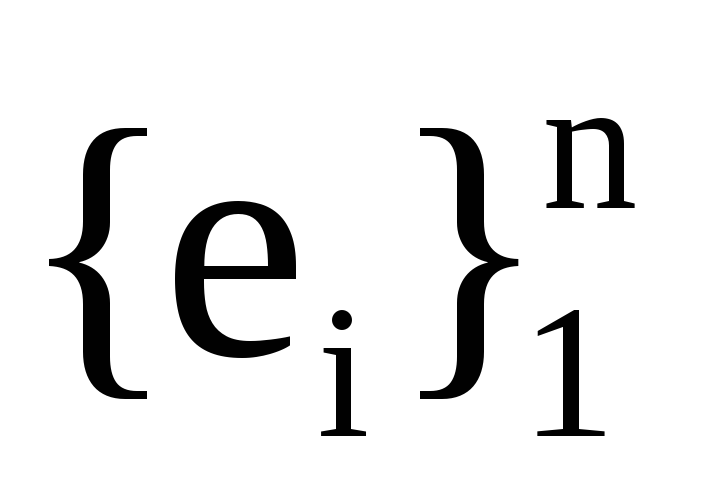 до базису
до базису
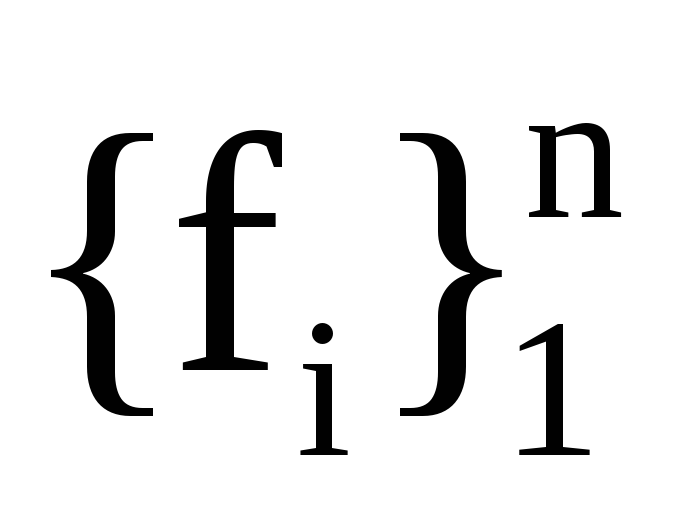 ,
Н― матриця переходу з базису
,
Н― матриця переходу з базису
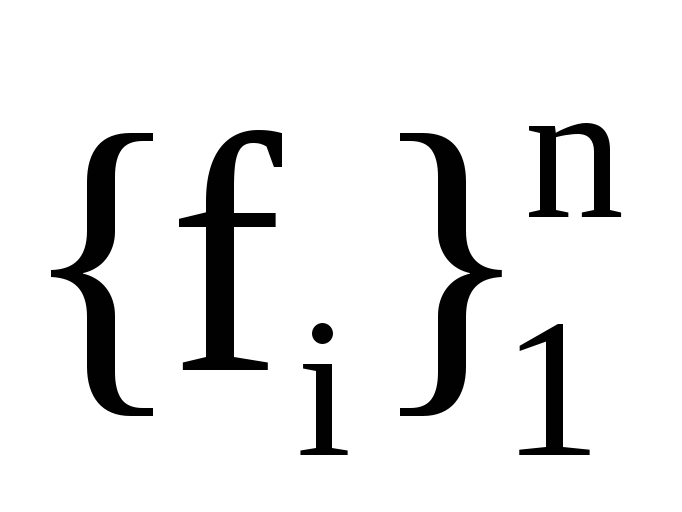 до базису
до базису
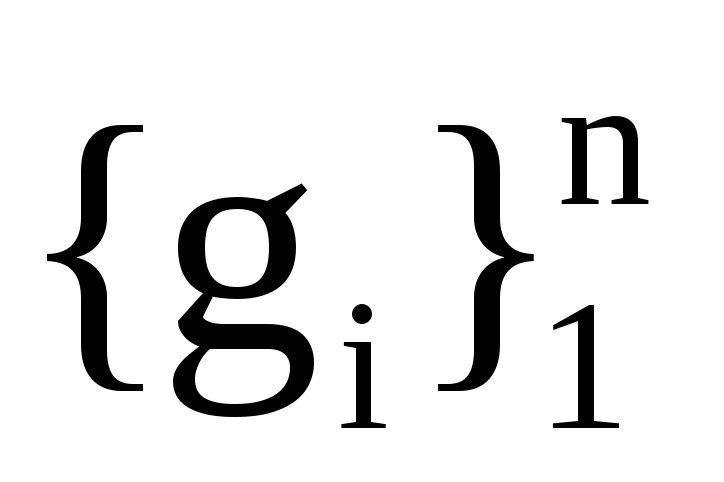 ,
а Т― матриця переходу з базису
,
а Т― матриця переходу з базису
 до базису
до базису
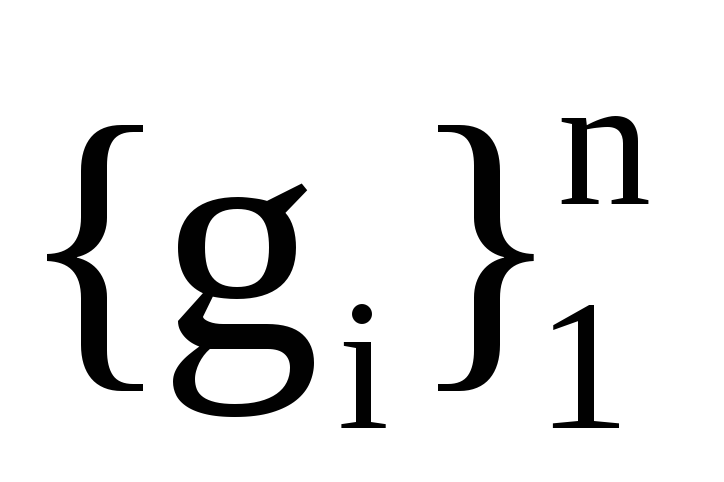 .
Тоді: а) Т=Р-1Н
; б) Т=НР; в) Т=РН; г) Т=Н-1Р.
.
Тоді: а) Т=Р-1Н
; б) Т=НР; в) Т=РН; г) Т=Н-1Р. -
Дайте визначення лінійної форми в унітарному просторі.
-
Яке позначення ми використовували для запису лінійної форми: а)
 ;
б)
;
б)
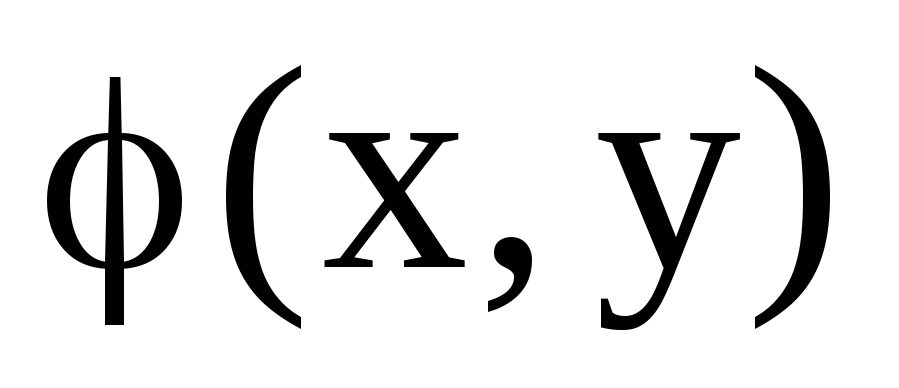 ;
в) Ах; г)
;
в) Ах; г)
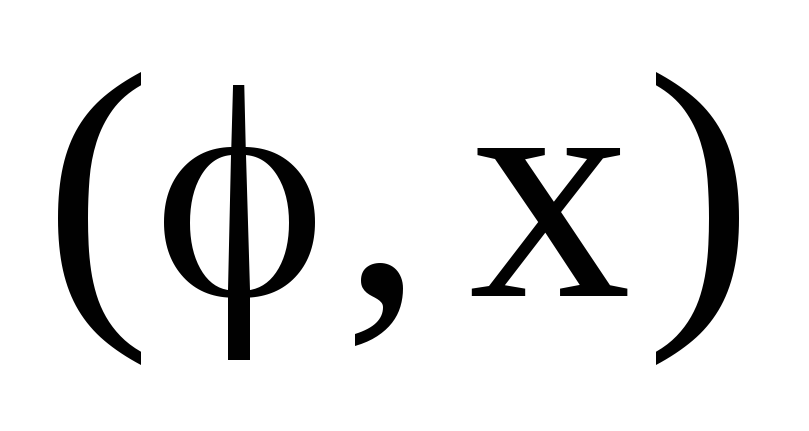 .
. -
Запишіть властивість адитивності лінійної форми.
-
Запишіть властивість однорідності лінійної форми.
-
Дайте визначення: що називається коефіцієнтами лінійної форми?
-
Сформулюйте теорему про спеціальне представлення лінійної форми в унітарному просторі.
-
За теоремою про спеціальне представлення лінійної форми лінійній формі у відповідність ставиться: а) вектор; б) матриця; в) оператор; г) число.
-
Лінійній формі
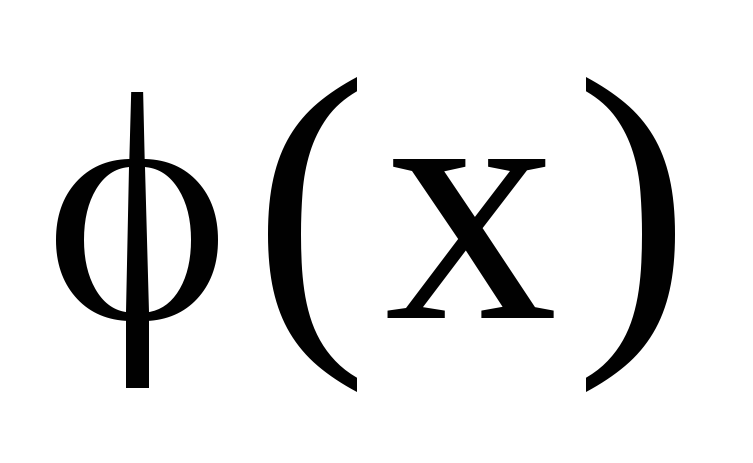 в унітарному просторі можна однозначно
поставити у відповідність вектор h
за наступним правилом: а)
в унітарному просторі можна однозначно
поставити у відповідність вектор h
за наступним правилом: а)
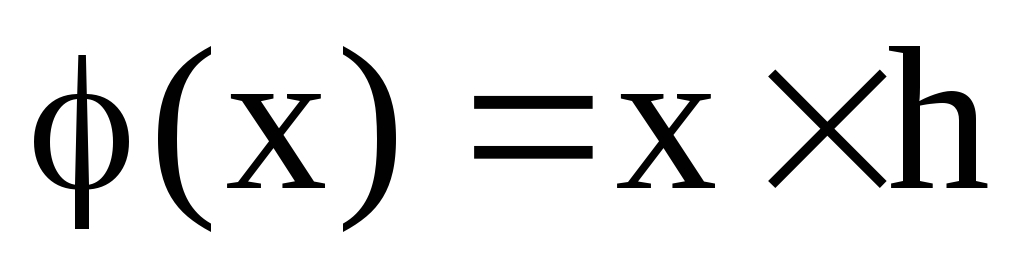 ;
б)
;
б)
 ;
в)
;
в)
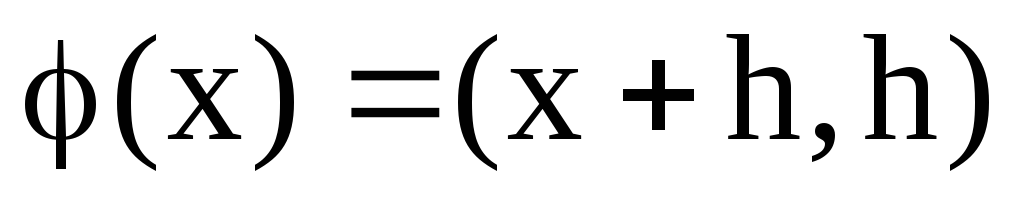 ;
г)
;
г)
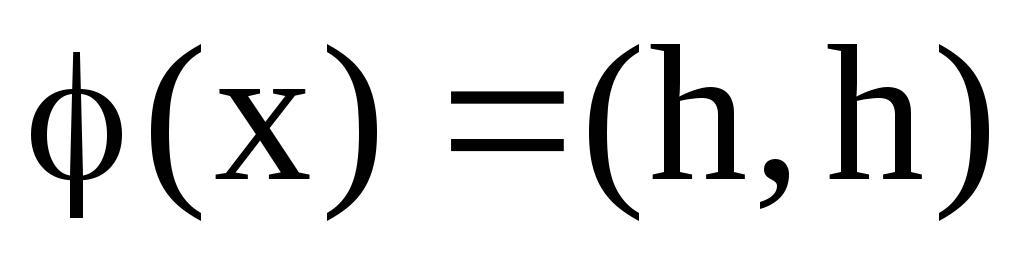 .
. -
Дайте визначення півторалінійної форми в унітарному просторі.
-
Яке позначення ми використовували для запису півторалінійної форми: а)
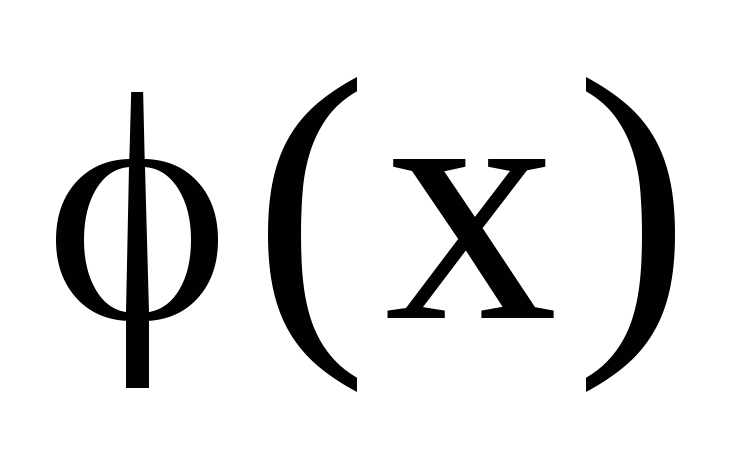 ;
б)
;
б)
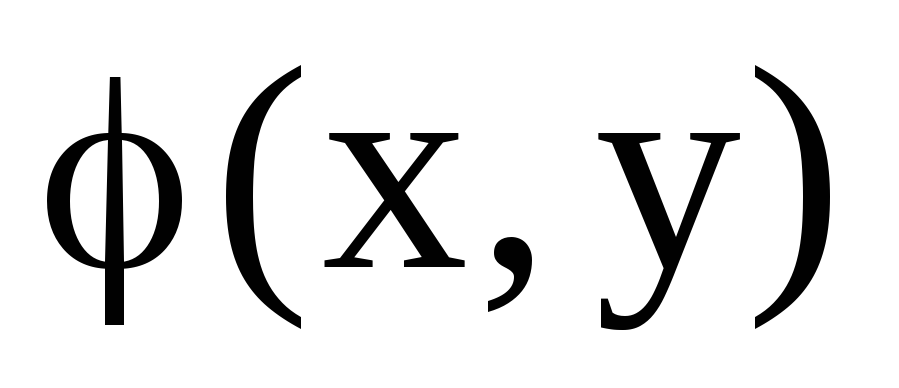 ;
в) Ах; г)
;
в) Ах; г)
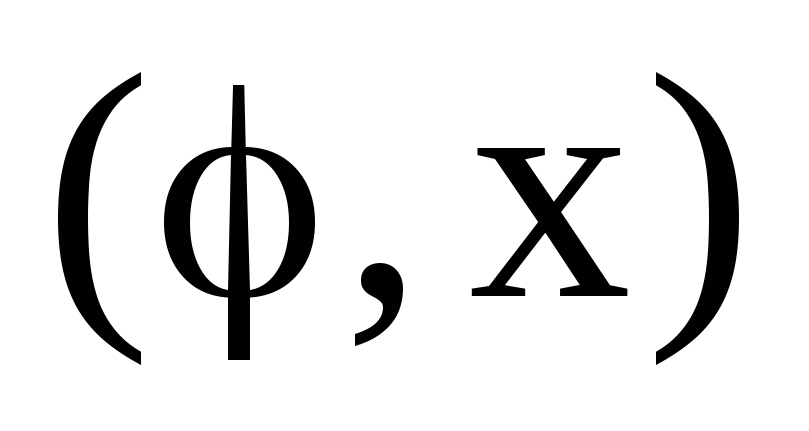 .
. -
Запишіть властивість адитивності півторалінійної форми за першим аргументом.
-
Запишіть властивість однорідності півторалінійної форми за першим аргументом.
-
Запишіть властивість адитивності півторалінійної форми за другим аргументом.
-
Для півторалінійної форми запишіть аналог властивості однорідності за другим аргументом.
-
Що являється аналогом півторалінійної форми в евклідовому просторі.
-
Що являється аналогом білінійної форми в унітарному просторі.
-
Дайте визначення матриці півторалінійної форми.
-
Сформулюйте теорему про спеціальне представлення півторалінійної форми.
-
За теоремою про спеціальне представлення півторалінійної форми півторалінійній формі у відповідність ставиться: а) вектор; б) матриця; в) оператор; г) число.
-
Півторалінійній формі
 в унітарному просторі можна однозначно
поставити у відповідність оператор А
за наступним правилом: а)
в унітарному просторі можна однозначно
поставити у відповідність оператор А
за наступним правилом: а)
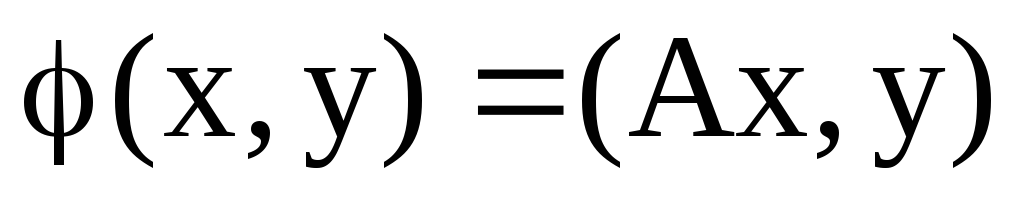 ;
б)
;
б)
 ;
в)
;
в)
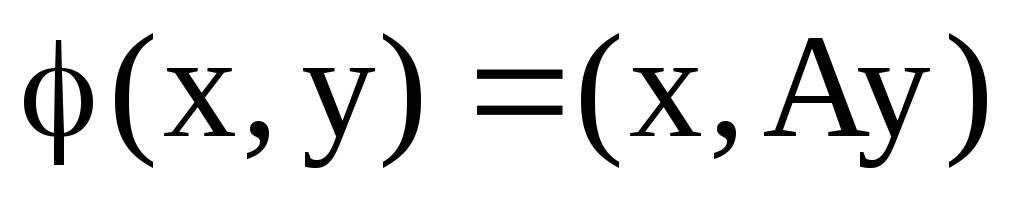 ;
г)
;
г)
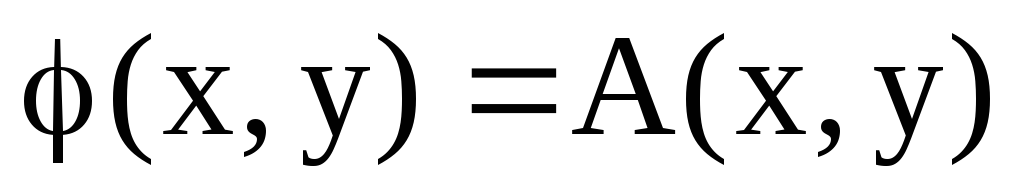 .
. -
Якщо
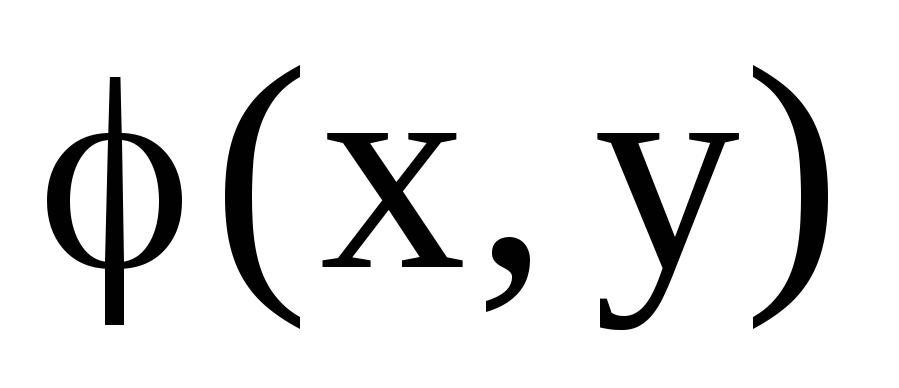 -
півторалінійна форма і А- оператор, які
пов’язані співвідношенням
-
півторалінійна форма і А- оператор, які
пов’язані співвідношенням
 ,
то оператор А називається: а) спряженим
до півторалінійної форми; б) приєднаним
до півторалінійної форми; в) полярним
до півторалінійної форми; г) оберненим
до півторалінійної форми.
,
то оператор А називається: а) спряженим
до півторалінійної форми; б) приєднаним
до півторалінійної форми; в) полярним
до півторалінійної форми; г) оберненим
до півторалінійної форми. -
Нехай
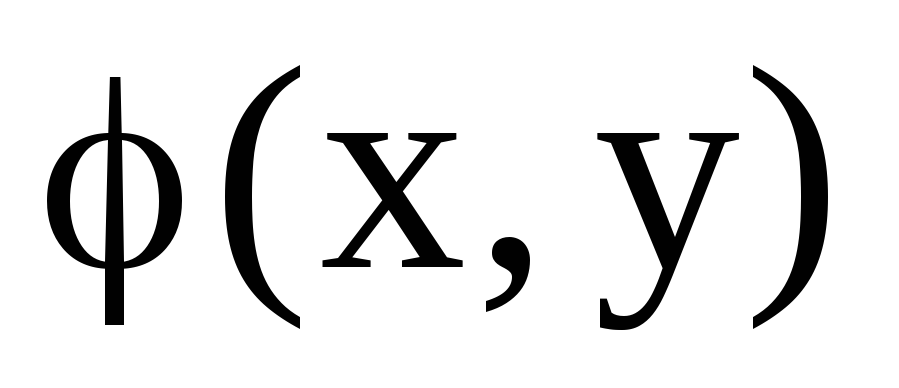 -
півторалінійна форма і А- лінійний
оператор, які пов’язані співвідношенням
-
півторалінійна форма і А- лінійний
оператор, які пов’язані співвідношенням
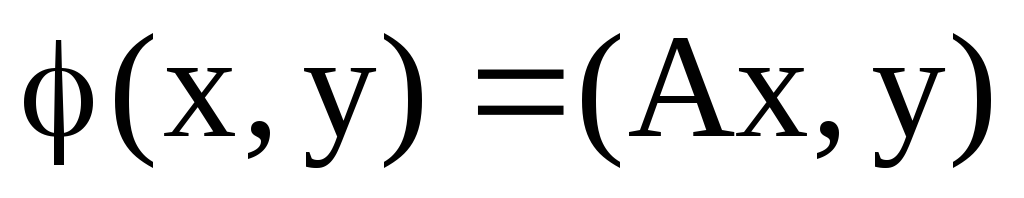 .
Якщо В- матриця зазначеної півторалінійної
форми і С- матриця зазначеного лінійного
оператора, то матриці В та С в
ортонормованому базисі пов’язані
співвідношенням: а) В=С; б) В=СТ;
в) В=С*;
а) В=
.
Якщо В- матриця зазначеної півторалінійної
форми і С- матриця зазначеного лінійного
оператора, то матриці В та С в
ортонормованому базисі пов’язані
співвідношенням: а) В=С; б) В=СТ;
в) В=С*;
а) В=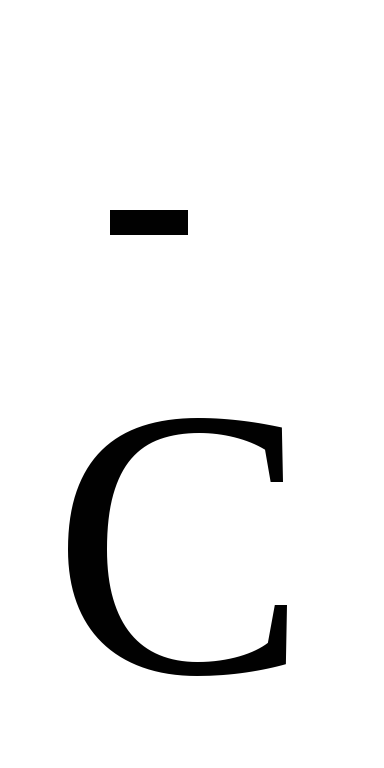 .
. -
Нехай
 -
півторалінійна форма і А- лінійний
оператор, які пов’язані співвідношенням
-
півторалінійна форма і А- лінійний
оператор, які пов’язані співвідношенням
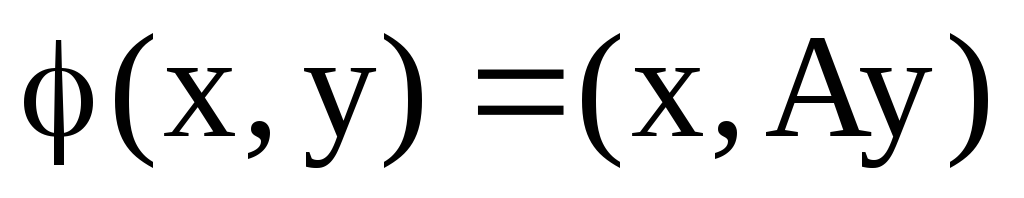 .
Якщо В- матриця зазначеної півторалінійної
форми і С- матриця зазначеного лінійного
оператора, то матриці В та С в
ортонормованому базисі пов’язані
співвідношенням: а) В=С; б) В=СТ;
в) В=С*;
а) В=
.
Якщо В- матриця зазначеної півторалінійної
форми і С- матриця зазначеного лінійного
оператора, то матриці В та С в
ортонормованому базисі пов’язані
співвідношенням: а) В=С; б) В=СТ;
в) В=С*;
а) В=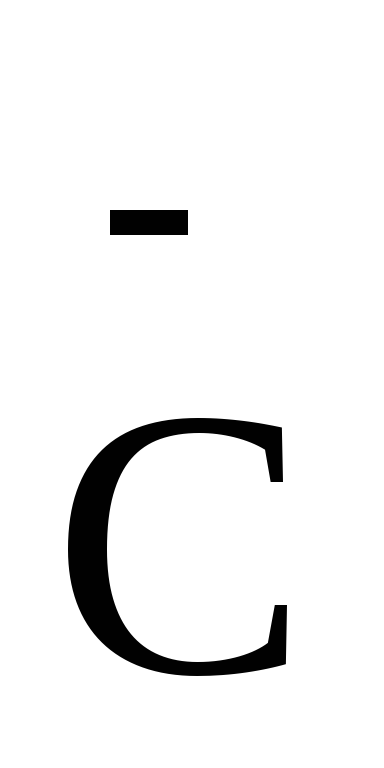 .
. -
Нехай
 -
півторалінійна форма, А та В- лінійні
оператори, які пов’язані співвідношенням
-
півторалінійна форма, А та В- лінійні
оператори, які пов’язані співвідношенням
 .
Якщо В- матриця зазначеної півторалінійної
форми, К- матриця лінійного оператора
А та М- матриця лінійного оператора В,
то матриці К та М в ортонормованому
базисі пов’язані співвідношенням: а)
К=М; б) К=МТ;
в) К=М*;
а) К=
.
Якщо В- матриця зазначеної півторалінійної
форми, К- матриця лінійного оператора
А та М- матриця лінійного оператора В,
то матриці К та М в ортонормованому
базисі пов’язані співвідношенням: а)
К=М; б) К=МТ;
в) К=М*;
а) К= .
. -
Дайте визначення лінійного оператора, спряженого до лінійного опертора А.
-
Як ми позначаємо спряжений лінійний оператор?
-
Визначення спряженого лінійного оператора задається через формулу: а) (Ах,у)=(А*х,у); б) (х,Ау)=(х,А*у); в) (Ах,у)=(х,А*у); г) (Ах,у)=А*(х,у).
-
Спираючись на властивості спряжених операторів, напишіть чому дорівнює Е*.
-
Спираючись на властивості спряжених операторів, напишіть чому дорівнює (А+В)*.
-
Спираючись на властивості спряжених операторів, напишіть чому дорівнює (
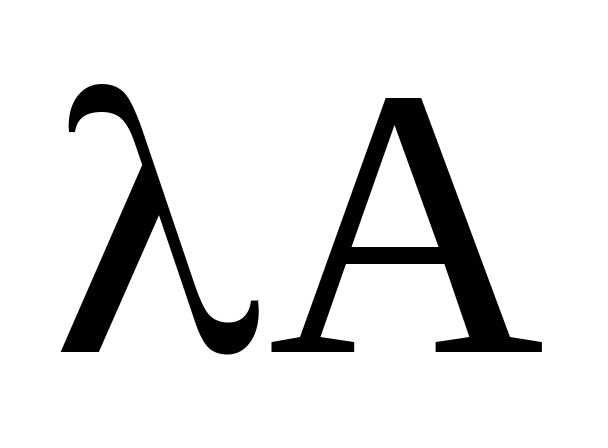 )*.
)*. -
Спираючись на властивості спряжених операторів, напишіть чому дорівнює (А*)*.
-
Спираючись на властивості спряжених операторів, напишіть чому дорівнює (АВ)*.
-
Спираючись на властивості спряжених операторів, напишіть чому дорівнює (А-1)*.
-
Дайте визначення ермітового оператора в унітарному просторі.
-
Дайте визначення самоспряженого оператора в евклідовому просторі.
-
Чим відрізняються визначення ермітового та самоспряженого операторів?
-
Сформулюйте теорему про спеціальне представлення лінійного оператора в унітарному просторі.
-
Запишіть формули, за якими будь- який лінійний оператор в унітарному просторі можна представити у вигляді суми двох ермітових операторів.
-
Дайте визначення дійсної частини лінійного оператора в унітарному просторі.
-
Дайте визначення уявної частини лінійного оператора в унітарному просторі.
-
Які два лінійні оператори називаються комутуючими?
-
За якої умови добуток двох ермітових операторів буде обов’язково ермітовим?
-
Якщо А- ермітів оператор, то що можна сказати про скалярний добуток (Ах,х), де х- довільний вектор унітарного простору (на основі теореми).
-
Якщо А- ермітів оператор та х- довільний вектор унітарного простору, то: а) (Ах,х)Є
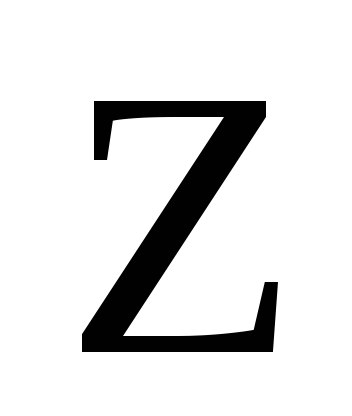 ;
б) (Ах,х)=0; в) (Ах,х)Є
;
б) (Ах,х)=0; в) (Ах,х)Є ;
г) (Ах,х)Є
;
г) (Ах,х)Є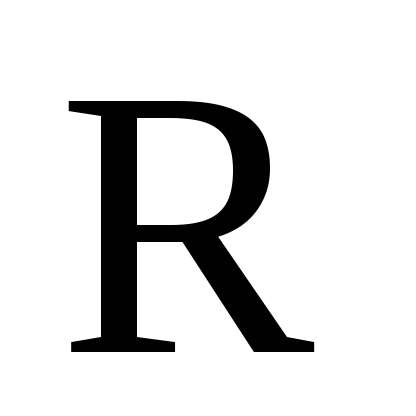 .
. -
Сформулюйте теорему про власні значення ермітового оператора.
-
Власні значення ермітового оператора є: а) цілими числами; б) завжди дорівнюють нулю; в) натуральними числами; г) дійсними числами.
-
Сформулюйте теорему про власні вектори ермітового оператора, які відповідають різним власним значенням.
-
Власні вектори ермітового оператора, які відповідають різним власним значенням є: а) колінеарними; б) однонаправленими; в) ортогональними; г) різнонаправленими.
-
Дайте визначення норми лінійного оператора.
-
Наслідком визначення норми лінійного оператора є співвідношення: а)
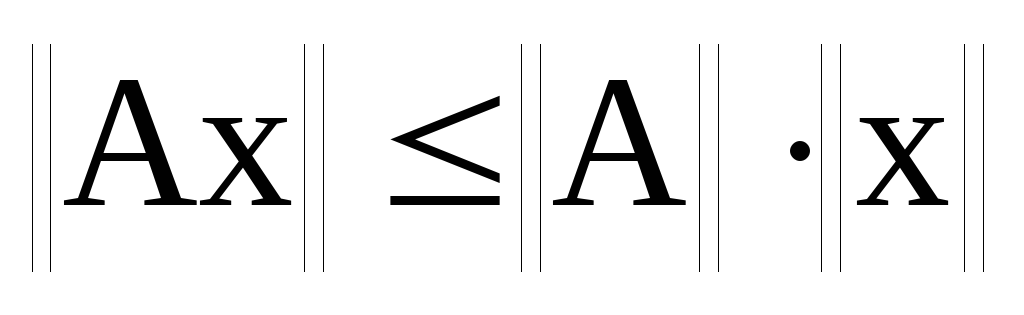 ;
б)
;
б)
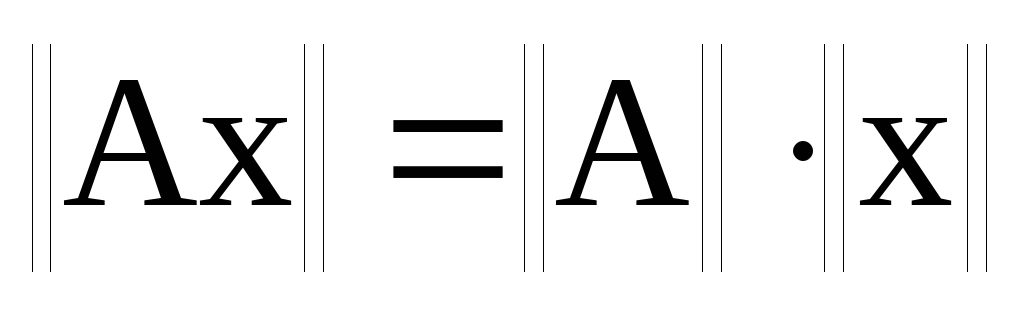 ;
в)
;
в)
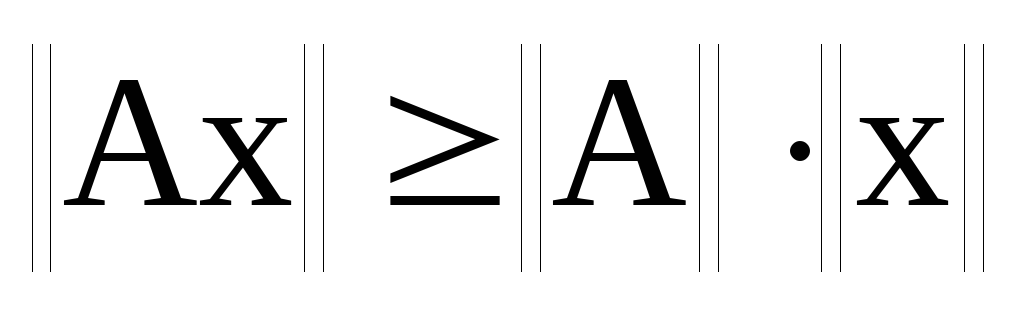 ;
г)
;
г)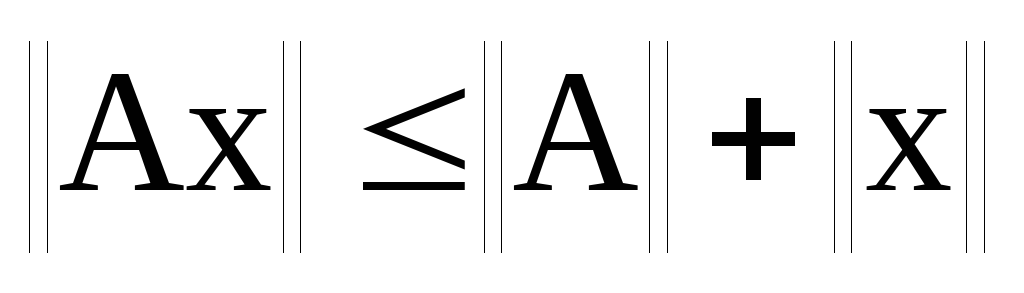 .
. -
За наслідком визначення норми лінійного оператора у якому випадку норма лінійного оператора дорівнює нулю?
-
Сформулюйте теорему про норму ермітового оператора.
-
Норма ермітового оператора дорівнює: а)
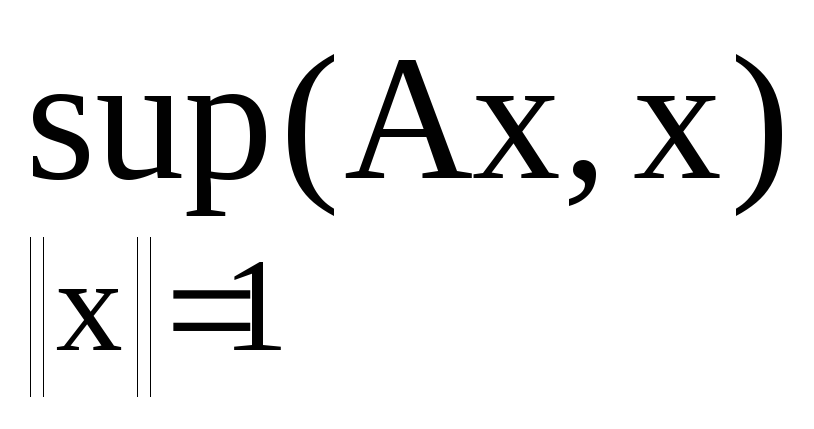 ;
б)
;
б)
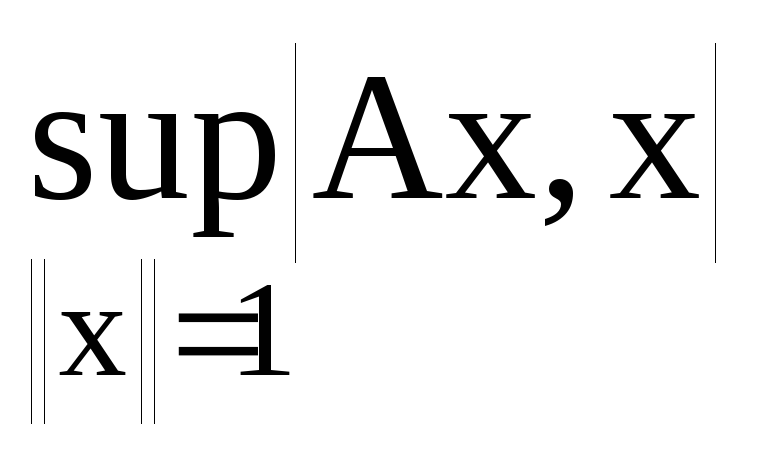 ;
в)
;
в)
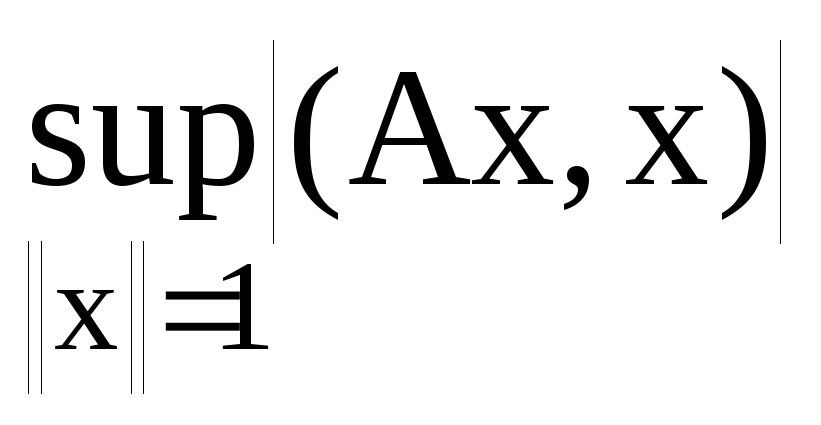 ;
г)
;
г)
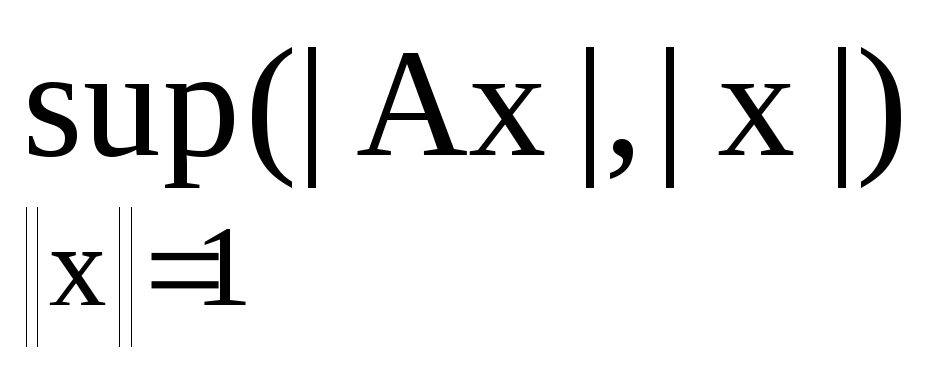 .
. -
Якщо А- ермітів оператор, то: а)
 ;
б)
;
б)
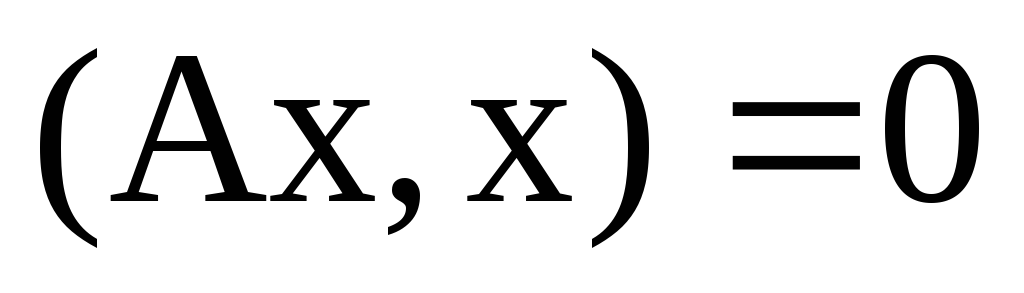 ;
в)
;
в)
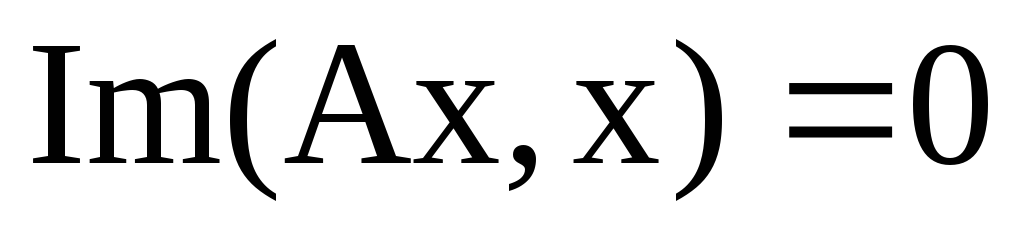 ;
г)
;
г)
 .
. -
Якщо А- ермітів оператор,
 -
його власне значення та х- відповідний
йому одиничний власний вектор, то за
якою формулою
-
його власне значення та х- відповідний
йому одиничний власний вектор, то за
якою формулою
 виражається через А та х (на основі
відповідної теореми)?
виражається через А та х (на основі
відповідної теореми)? -
Якщо А- ермітів оператор,
 -
його власне значення та х- відповідний
йому одиничний власний вектор, то: а)
-
його власне значення та х- відповідний
йому одиничний власний вектор, то: а)
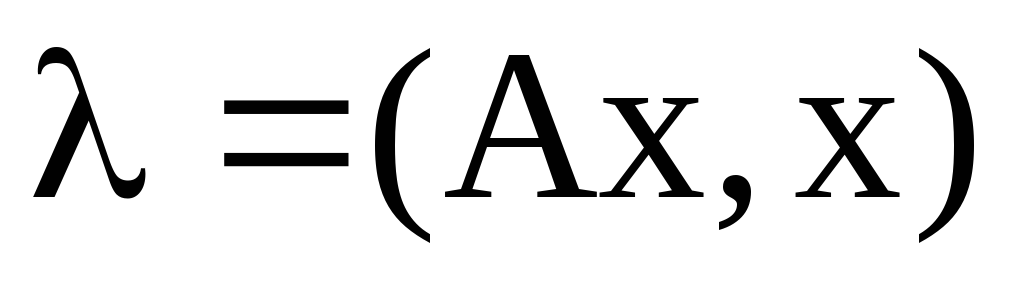 ;
б)
;
б)
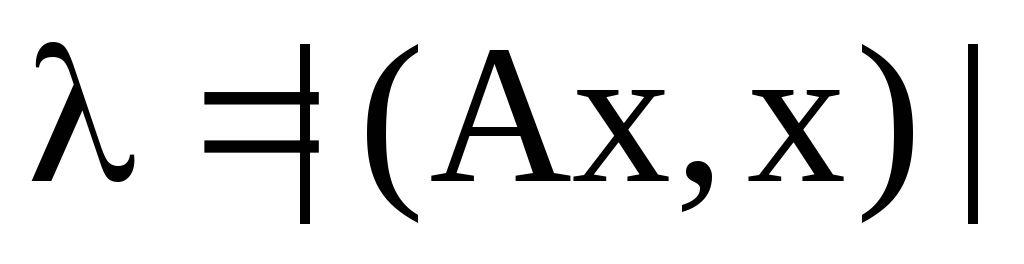 ;
в)
;
в)
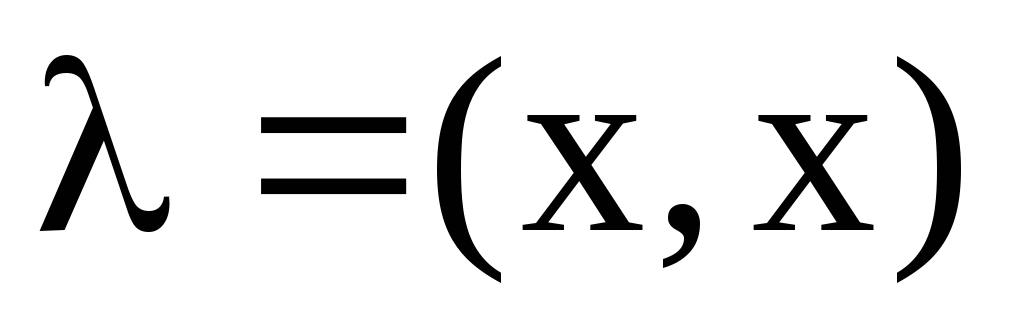 ;
г)
;
г)
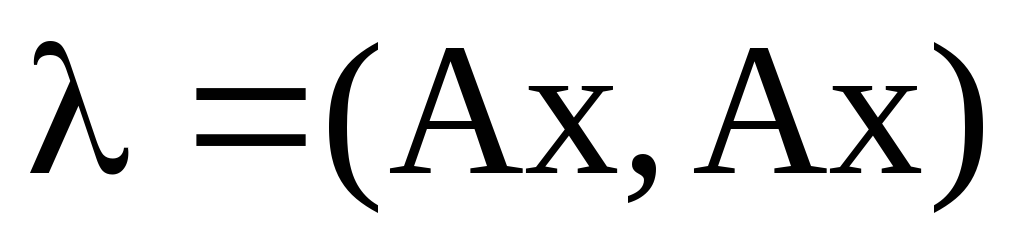 .
. -
Нехай А- ермітів оператор та
 -
його власне значення. Якщо
-
його власне значення. Якщо
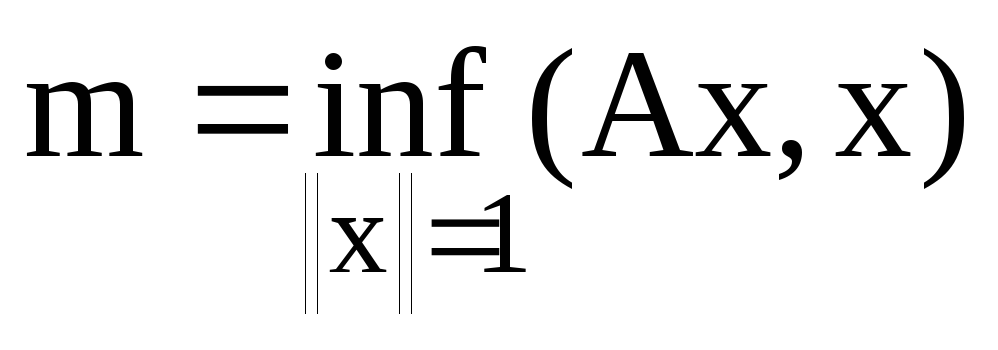 та
та
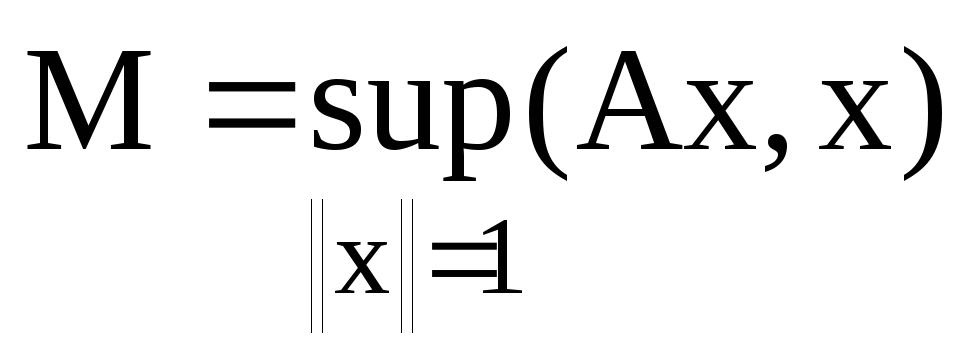 то: а)
то: а)
 ;
б)
;
б)
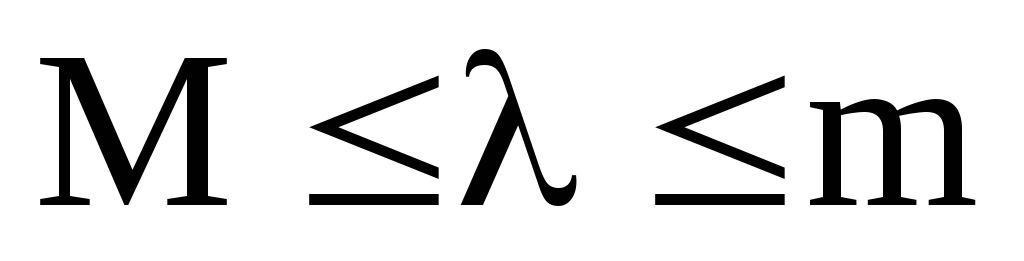 ;
в)
;
в)
 ;
г)
;
г)
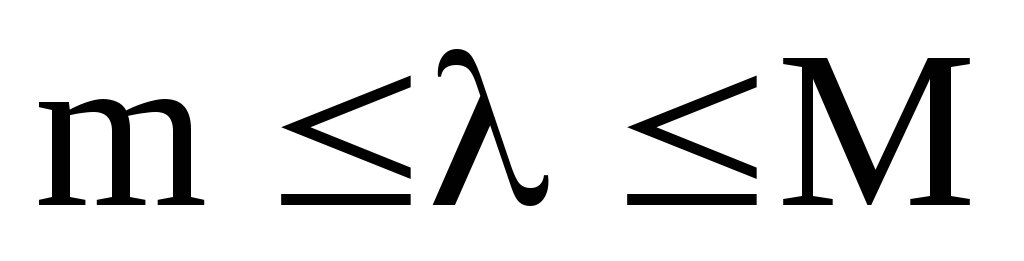 .
. -
Нехай А- ермітів оператор та х- довільний вектор унітарного простору. Якщо
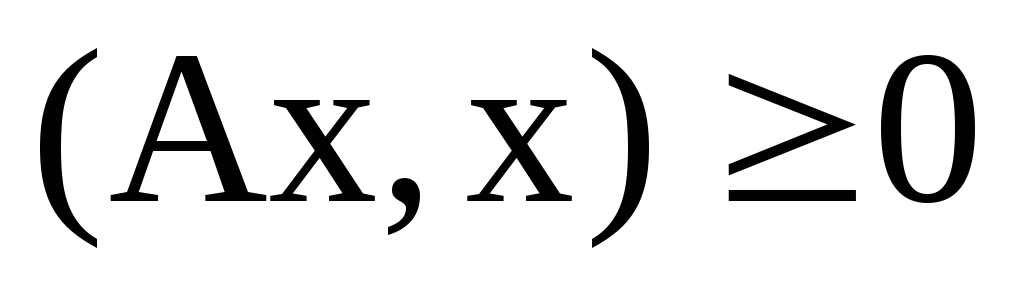 ,
то: а)
,
то: а)
 ,
б)
,
б)
 ;
в)
;
в)
 ;
г)
;
г)
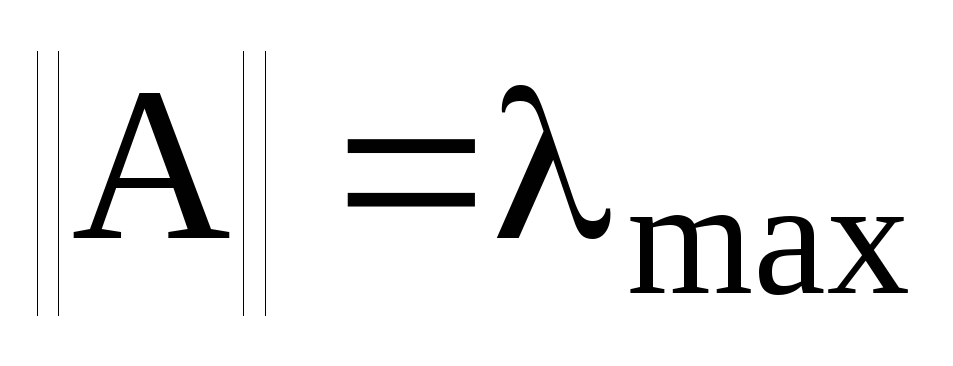 .
. -
Нехай А- ермітів оператор та
 -
його власне значення. Якщо
-
його власне значення. Якщо
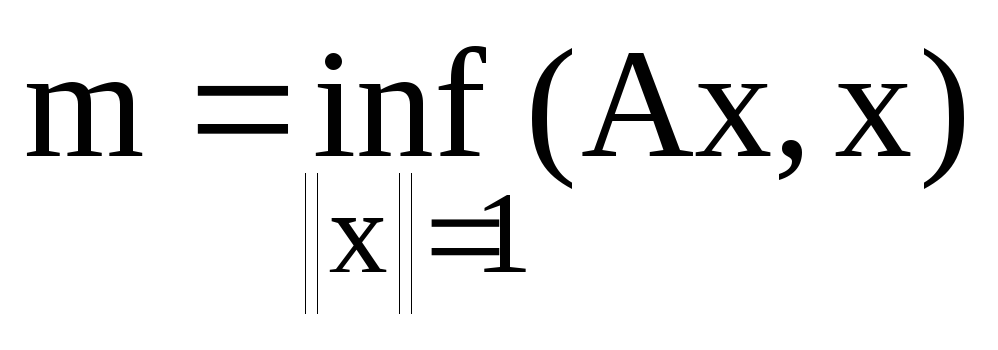 та
та
 то: а)
то: а)
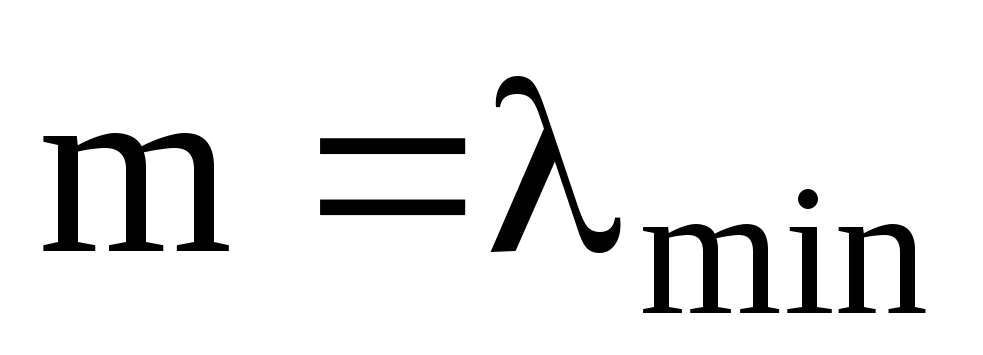 ,
,
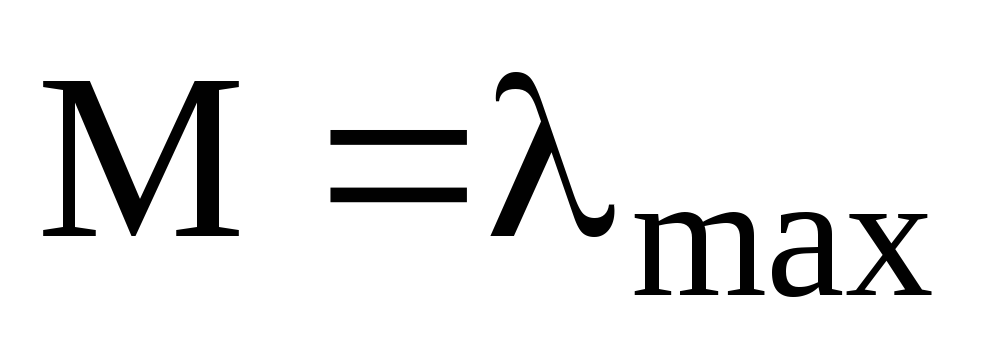 ;
б)
;
б)
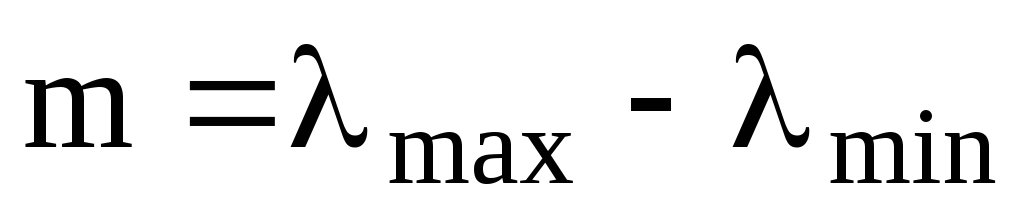 ,
,
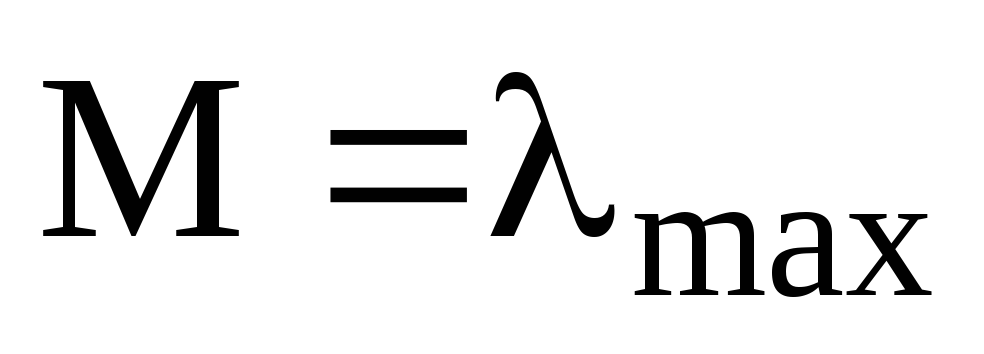 ;
в)
;
в)
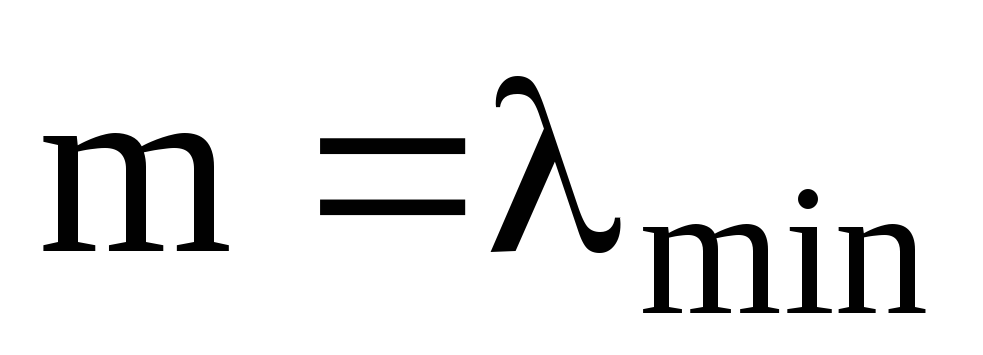 ,
,
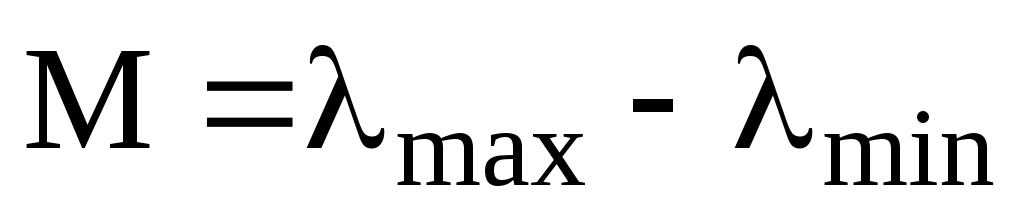 ;
г)
;
г)
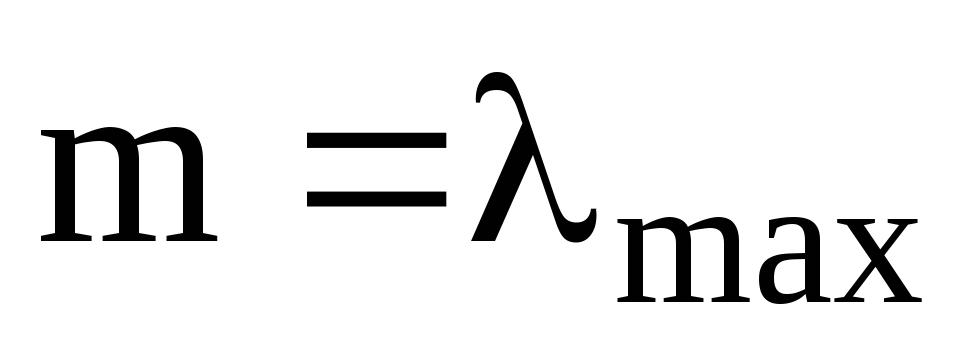 ,
,
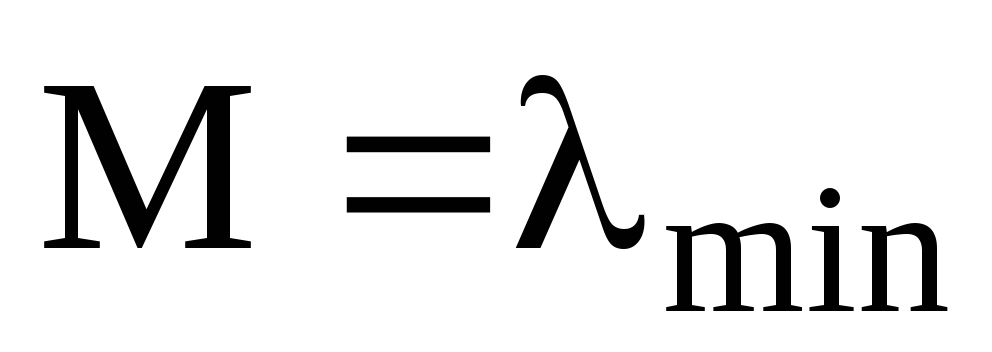 .
. -
Сформулюйте теорему про власний базис ермітового оператора.
-
У якому порядку ми домовлялися нумерувати власні значення ермітового оператора?
-
Сформулюйте теорему про мінімаксну властивість власних значень ермітового оператора.
-
Запишіть формулу, на основі якої формулюється теорема про мінімаксну властивість власних значень ермітового оператора?
-
Дайте визначення проектора на одновимірний підпростір, який задається вектором
 .
. -
Проектор на одновимірний підпростір, який задається вектором
 ,
визначається наступною формулою: а)
,
визначається наступною формулою: а)
 ;
б)
;
б)
 ;
в)
;
в)
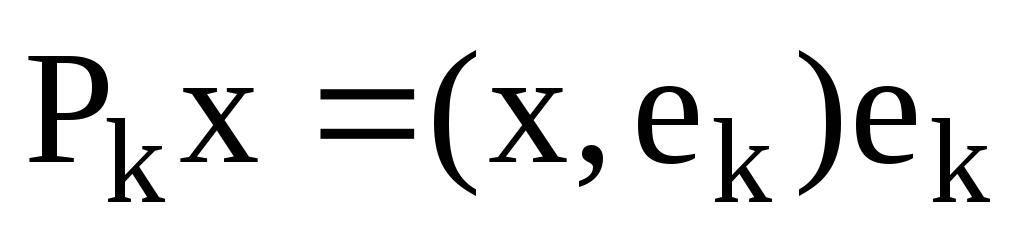 ;
г)
;
г)
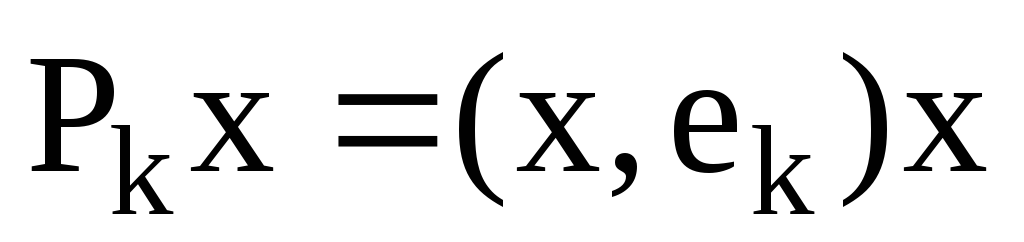 .
. -
Якщо
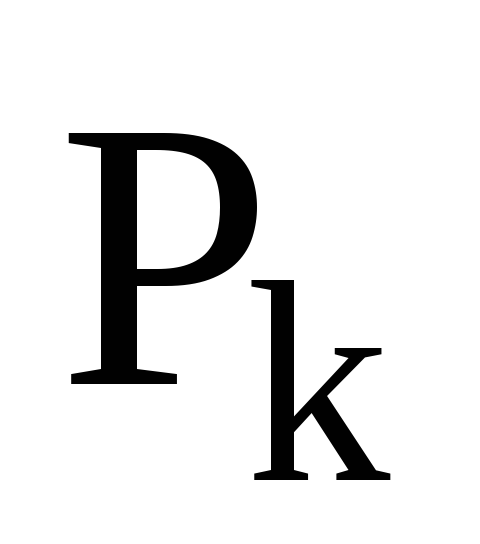 -
проектор, то цей оператор є обов’язково:
а) унітарним; б) нормальним; в) ермітовим.
-
проектор, то цей оператор є обов’язково:
а) унітарним; б) нормальним; в) ермітовим. -
На основі властивостей проектора
 чому дорівнює добуток операторів
чому дорівнює добуток операторів
 ,
якщо
,
якщо
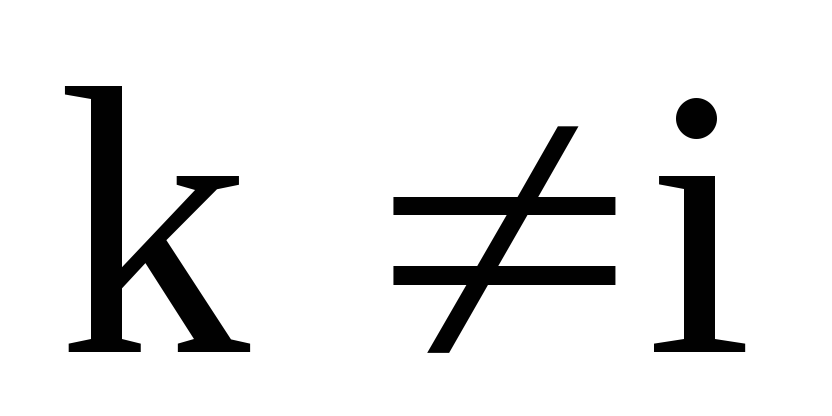 ?
? -
На основі властивостей проектора
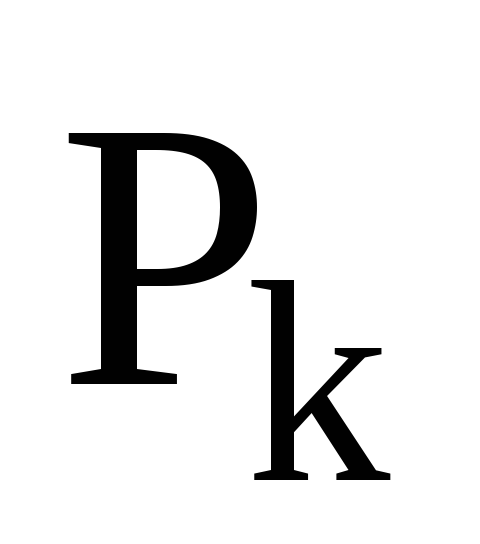 чому дорівнює добуток операторів
чому дорівнює добуток операторів
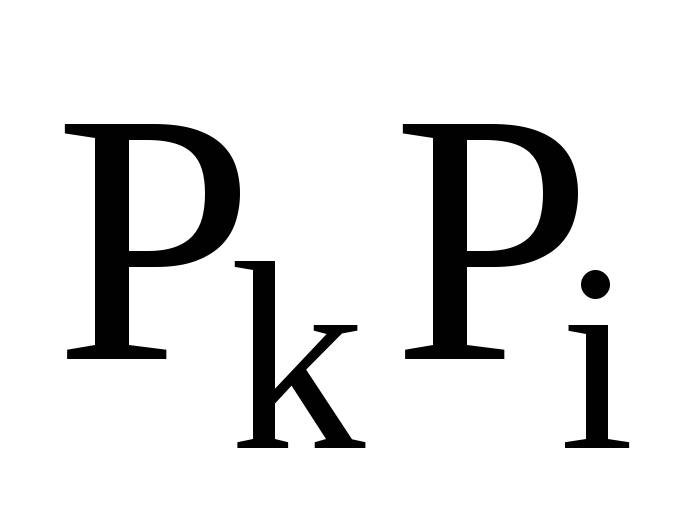 ,
якщо
,
якщо
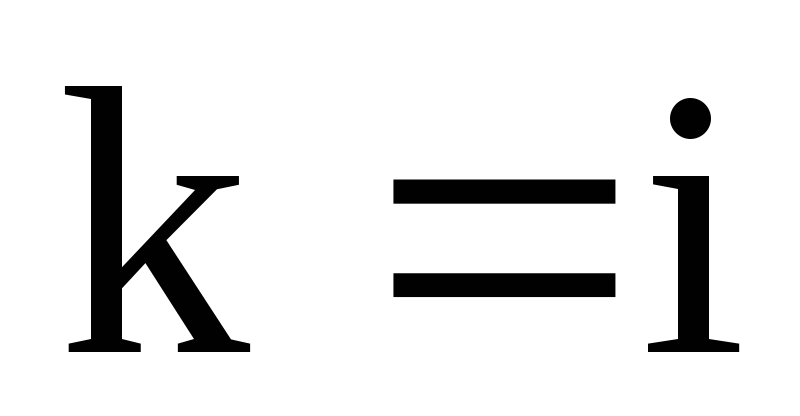 ?
? -
На основі властивостей проектора
 чому дорівнює
вираз
чому дорівнює
вираз
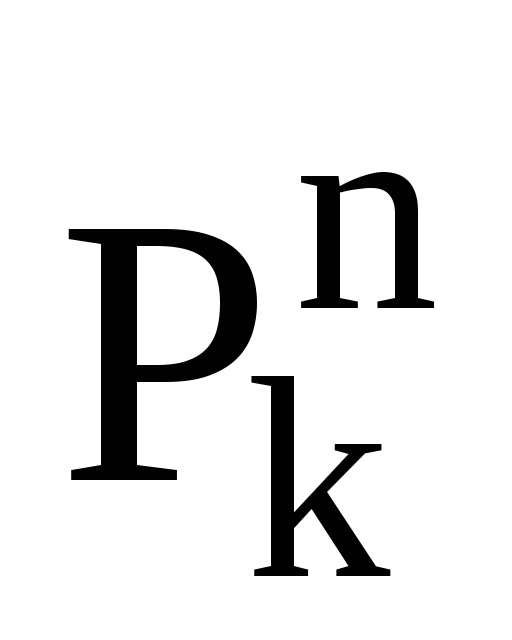 ,
де n- натуральнее число?
,
де n- натуральнее число? -
Запишіть формулу представлення довільного вектора унітарного простору через суму проекторів.
-
Якщо
 -
множина усіх проекторів унітарного
простору, які відповідають базису
-
множина усіх проекторів унітарного
простору, які відповідають базису
 ,
то чому дорівнює вираз
,
то чому дорівнює вираз
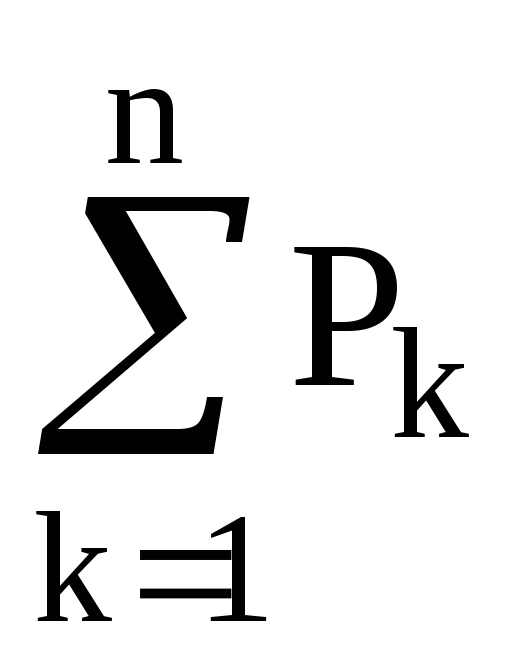 ?
? -
Якщо
 -
множина усіх проекторів унітарного
простору, які відповідають базису
-
множина усіх проекторів унітарного
простору, які відповідають базису
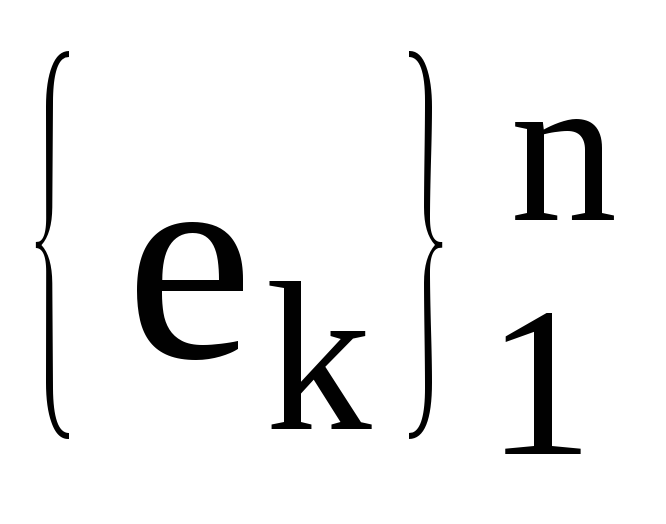 ,
то: а)
,
то: а)
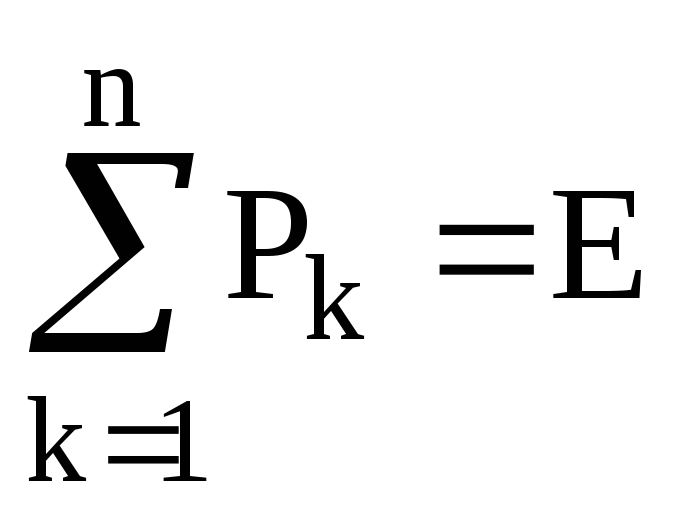 ;
б)
;
б)
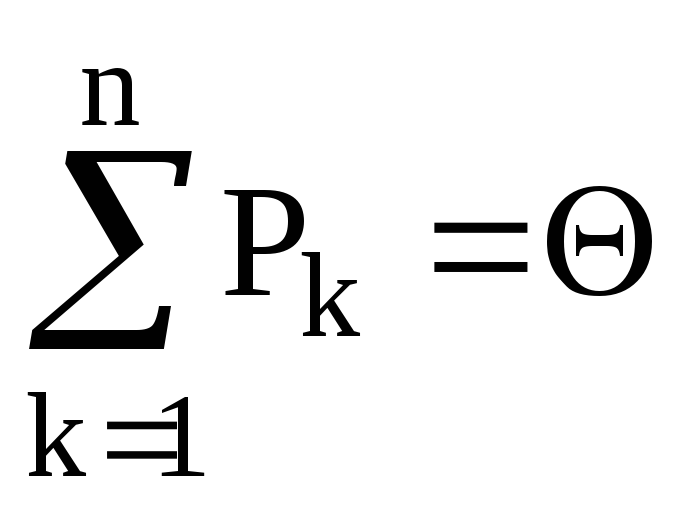 ;
в)
;
в)
 ;
г)
;
г)
 .
. -
Запишіть формулу спектрального розкладання ермітового оператора А.
-
Формула спектрального розкладання ермітового оператора А виглядає: а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
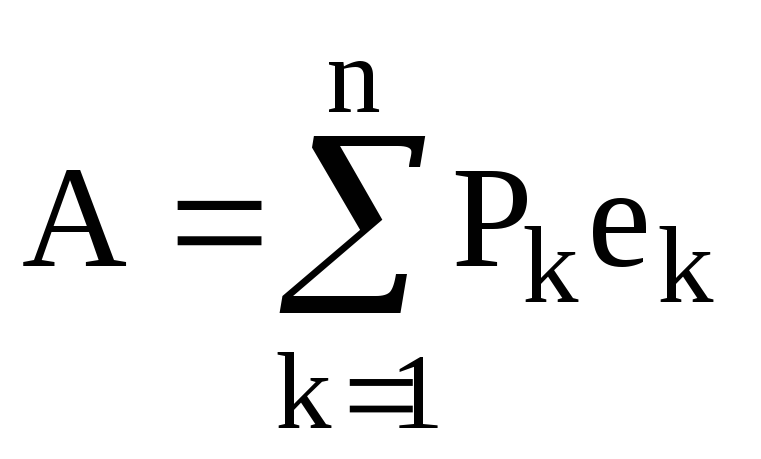 .
. -
Дайте визначення полінома від оператора.
-
Поліном від ермітового оператора через суму за проекторами записується як: а)
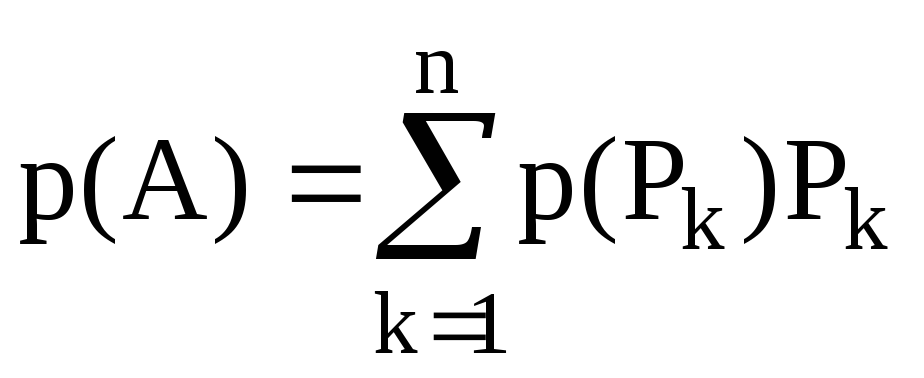 ;
б)
;
б)
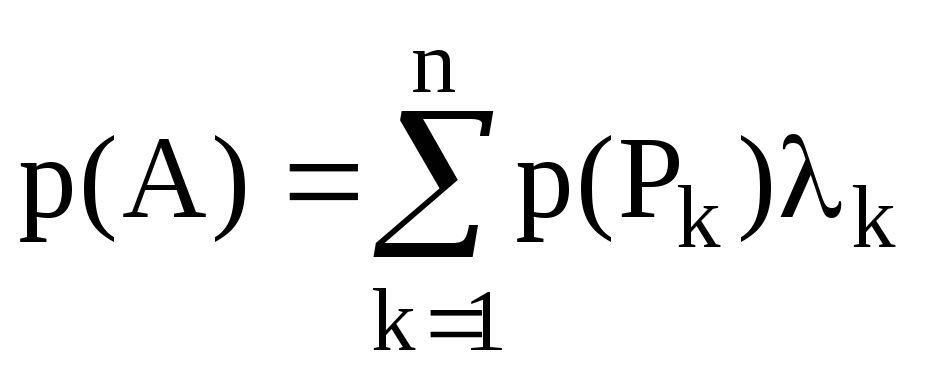 ;
в)
;
в)
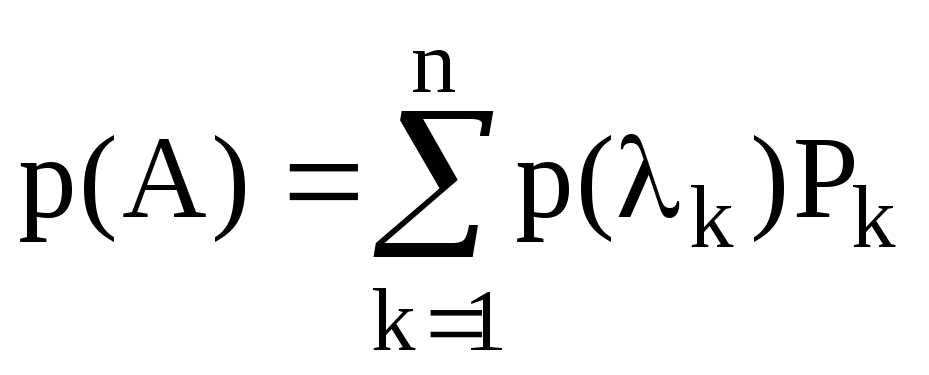 ;
г)
;
г)
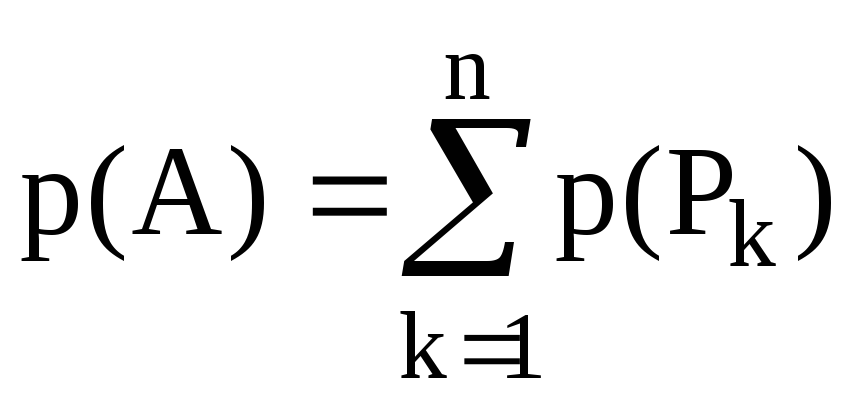 .
. -
Сформулюйте теорему Гамільтона- Келі.
-
Дайте визначення який термітів оператор називається додатнім.
-
Дайте визначення який термітів оператор називається додатно визначеним.
-
Дайте визначення який термітів оператор називається від’ємним.
-
Дайте визначення який термітів оператор називається від’ємно визначеним.
-
Власні значення додатного оператора є: а) додатними; б) невід’ємними; в) від’ємними; г) недодатними.
-
Власні значення додатно визначеного оператора є: а) додатними; б) невід’ємними; в) від’ємними; г) недодатними.
-
Власні значення від’ємного оператора є: а) додатними; б) невід’ємними; в) від’ємними; г) недодатними.
-
Власні значення від’ємно визначеного оператора є: а) додатними; б) невід’ємними; в) від’ємними; г) недодатними.
-
Дайте визначення кореня натурального степеня з додатного ермітового оператора.
-
На основі визначення кореня натурального степеня з додатно визначеного ермітового оператора опишіть процедуру знаходження такого кореня (тематика одного з домашніх завдань).
-
Дайте визначення яка півторалінійна форма називається ермітовою.
-
Оператор, приєднаний до ермітової півторалінійної форми, є: а) унітарним; б) нормальним; в) ермітовим.
-
Значення ермітової півторалінійної форми є: а) додатними; б) невід’ємними; в) дійсними; г) від’ємними.
-
Дайте визначення квадратичної форми в унітарному просторі.
-
Сформулюйте теорему про приведення ермітової форми до канонічного вигляду.
-
Сформулюйте теорему про одночасне приведення пари квадратичних форм до канонічного вигляду.
-
Як саме задається скалярний добуток в задачі одночасного приведення пари квадратичних форм до канонічного вигляду?
-
Запишіть формулою як виглядає ермітова квадратична форма після її приведення до канонічного вигляду (на основі відповідної теореми).
-
Запишіть формулами як виглядають квадратичні форми після їх приведення до канонічного вигляду (на основі теореми про одночасне приведення пари квадратичних форм до канонічного вигляду).
-
Дайте визначення унітарного оператора.
-
Якою літерою ми позначали на лекції унітарні оператори?
-
Чому дорівнює норма унітарного оператора?
-
Чому дорівнюють власні значення унітарного оператора?
-
Якщо оператор U- є унітарним, то: а)
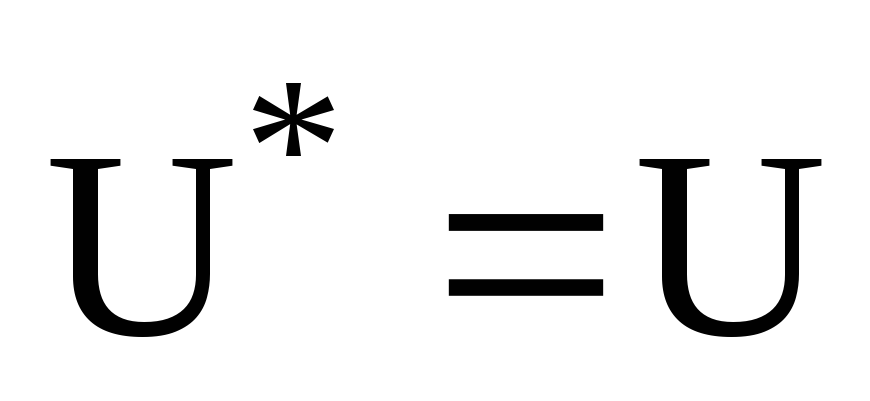 ;
б)
;
б)
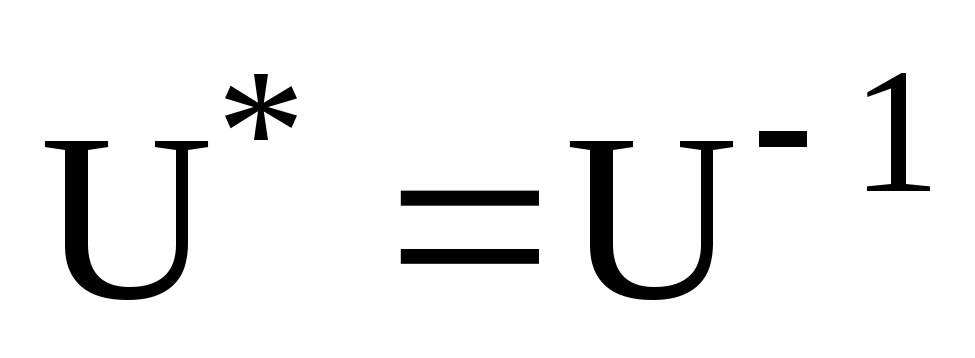 ;
в)
;
в)
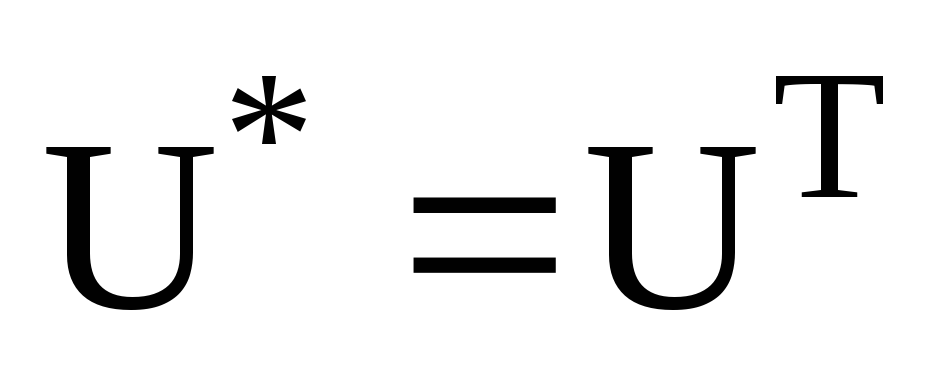 ;
г)
;
г)
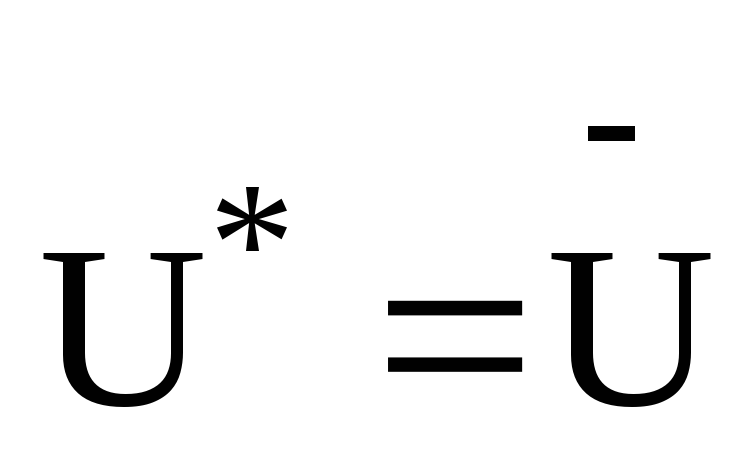 .
. -
Дайте визначення унітарної матриці.
-
Дайте визначення нормального оператора.
-
Наскільки справедливим є кожне з наступних тверджень. Будь- який нормальний оператор є: а) ермітовим; б) унітарним.
-
Наскільки справедливим є кожне з наступних тверджень. Будь- який ермітів оператор є: а) нормальним; б) унітарним.
-
Наскільки справедливим є кожне з наступних тверджень. Будь- який унітарний оператор є: а) ермітовим; б) нормальним.
-
Наскільки справедливим є кожне з наступних тверджень. Довільний нормальний оператор не обов’язково є: а) ермітовим; б) унітарним.
-
Наскільки справедливим є кожне з наступних тверджень. Довільний ермітів оператор не обов’язково є: а) нормальним; б) унітарним.
-
Наскільки справедливим є кожне з наступних тверджень. Довільний унітарний оператор не обов’язково є: а) ермітовим; б) нормальним.
-
Якщо А- нормальний оператор та
 -
його власне значення, то: а)
-
його власне значення, то: а)
 -
власне значення оператора А*;
б) (
-
власне значення оператора А*;
б) ( )-
власне значення оператора А*;
в)
)-
власне значення оператора А*;
в)
 -
власне значення оператора А*.
-
власне значення оператора А*. -
Якщо А- нормальний оператор, то оператори А та А*: а) мають усі спільні власні вектори; б) не мають спільних власних векторів; в) мають як спільні, так і різні власні вектори.
-
Для яких з наступних операторів існує власний ортонормований базис: а) нормальний; б) ермітів; в) унітарний.
-
Корені характеристичного рівняння є власними значеннями відповідного лінійного оператора: а) і в унітарному просторі, і в евклідовому просторі; б) в унітарному, але не в евклідовому просторі; в) в евклідовому, але не в унітарному просторі; г) ні в унітарному просторі, ні в евклідовому просторі.
-
Власні значення лінійного оператора є коренями характеристичного рівняння: а) і в унітарному просторі, і в евклідовому просторі; б) в унітарному, але не в евклідовому просторі; в) в евклідовому, але не в унітарному просторі; г) ні в унітарному просторі, ні в евклідовому просторі.
-
Аналогом унітарного оператора (з унітарного простору) в евклідовому просторі є: а) ермітів оператор; б) ортогональний оператор; в) самоспряжений оператор; г) нормальний оператор.
-
Аналогом ермітового оператора (з унітарного простору) в евклідовому просторі є: а) унітарний оператор; б) ортогональний оператор; в) самоспряжений оператор; г) нормальний оператор.
-
Аналогом ортогонального оператора (з евклідового простору) в унітарному просторі є: а) ермітів оператор; б) унітарний оператор; в) самоспряжений оператор; г) нормальний оператор.
-
Аналогом самоспряженого оператора (з евклідового простору) в унітарному просторі є: а) ермітів оператор; б) унітарний оператор; в) ортогональний оператор; г) нормальний оператор.
-
Дайте визначення ортогонального оператора в евклідовому просторі.
-
Якщо оператор Р- є ортогональним, то: а)
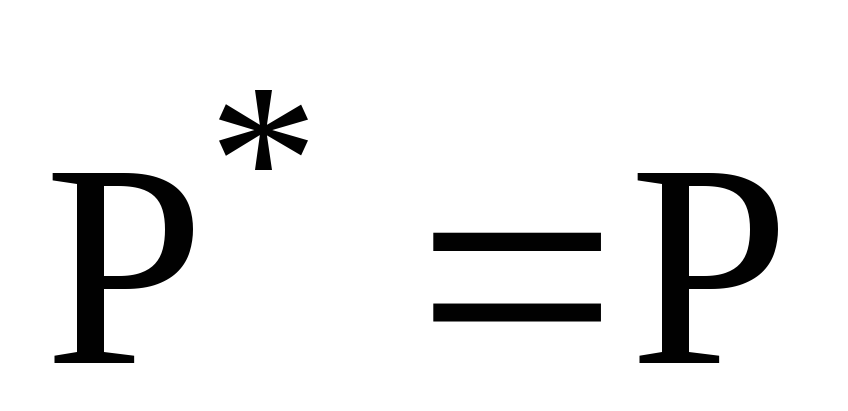 ;
б)
;
б)
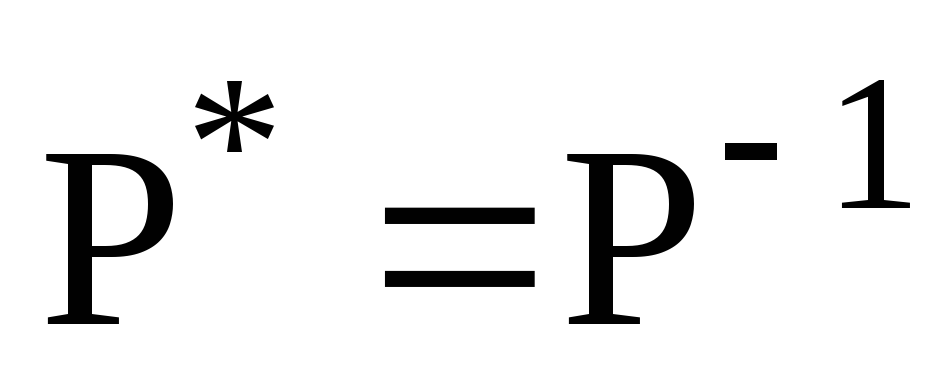 ;
в)
;
в)
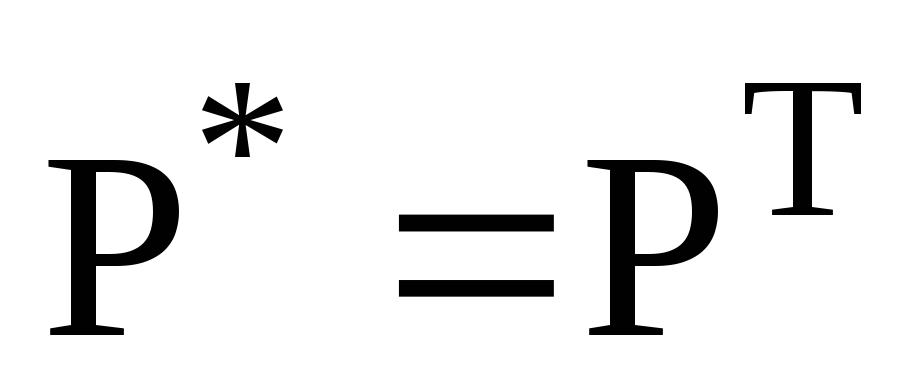 ;
г)
;
г)
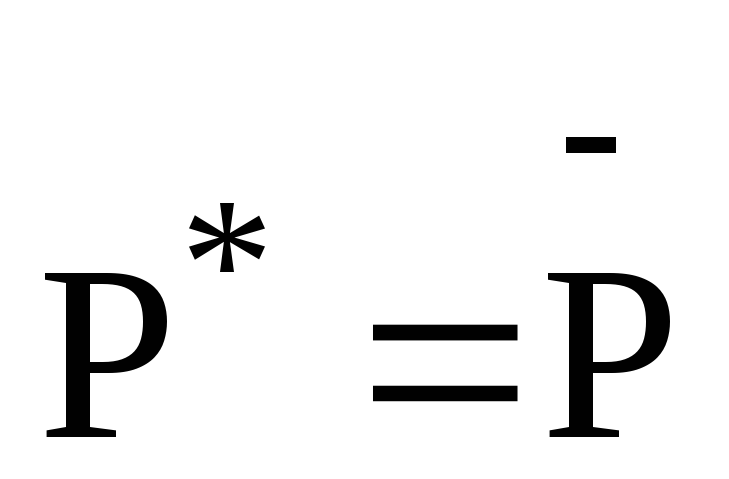 .
. -
Дайте визначення ортогональної матриці.
-
Запишіть формулою визначення ортогональної матриці.
-
Які властивості має матриця переходу із ортонормованого базису в ортонормований базис?
-
Запишіть ортогональні матриці одновимірних перетворень.
-
Запишіть ортогональні матриці двовимірних перетворень.
-
Запишіть матрицю двовимірного власного ортогонального перетворення.
-
Запишіть матрицю двовимірного невласного ортогонального перетворення.
-
Яке перетворення лінійного простору описує одновимірне власне ортогональне перетворення?
-
Яке перетворення лінійного простору описує одновимірне невласне ортогональне перетворення?
-
Яке перетворення лінійного простору описує двовимірне власне ортогональне перетворення?
-
Яке перетворення лінійного простору описує двовимірне невласне ортогональне перетворення?
-
Опишіть загальний вид матриці n- вимірного ортогонального перетворення.
-
Яка форма в евклідовому просторі є аналогом ермітової форми в унітарному просторі?
-
Яка форма в унітарному просторі є аналогом симетричної білінійної форми в евклідовому просторі?
-
Дайте визначення стаціонарної (критичної) точки функції f(x) на поверхні S.
-
Як називається точка на поверхні S, у якій похідна від функції f(x) вздовж будь- якого напрямку на поверхні S дорівнює нулю?
-
Дайте визначення стаціонарних (критичних) значень функції f(x) на поверхні S.
-
Дайте визначення одиничної сфери евклідового простору.
-
Запишіть формулою визначення одиничної сфери в евклідовому просторі.
-
Якими з наступних формул задається одинична сфера в евклідовому просторі: а)
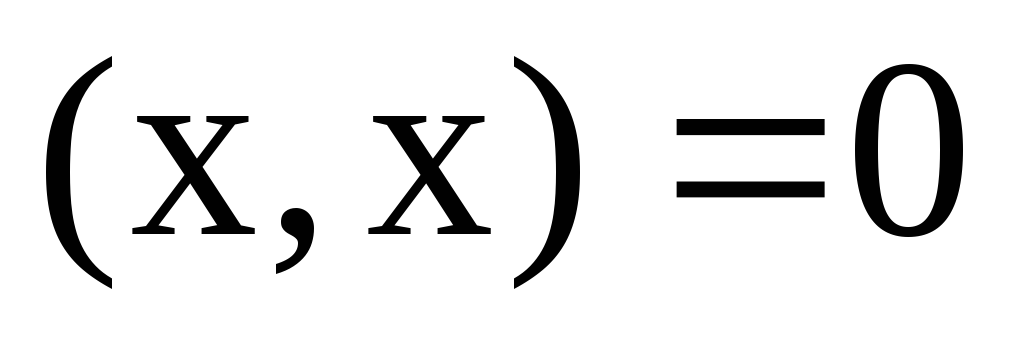 ;
б)
;
б)
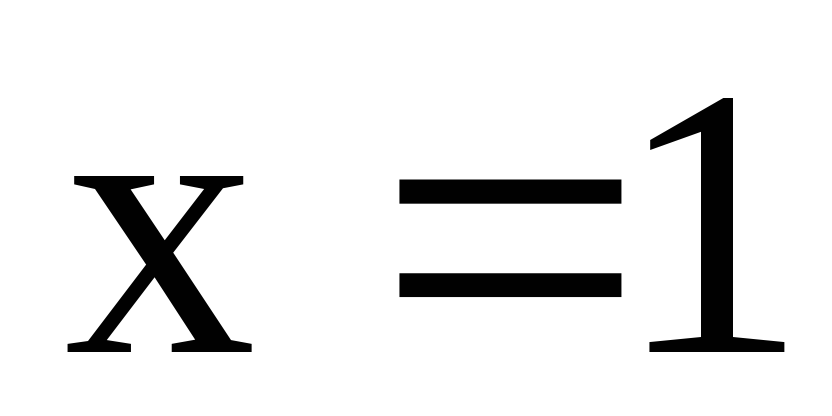 ;
в)
;
в)
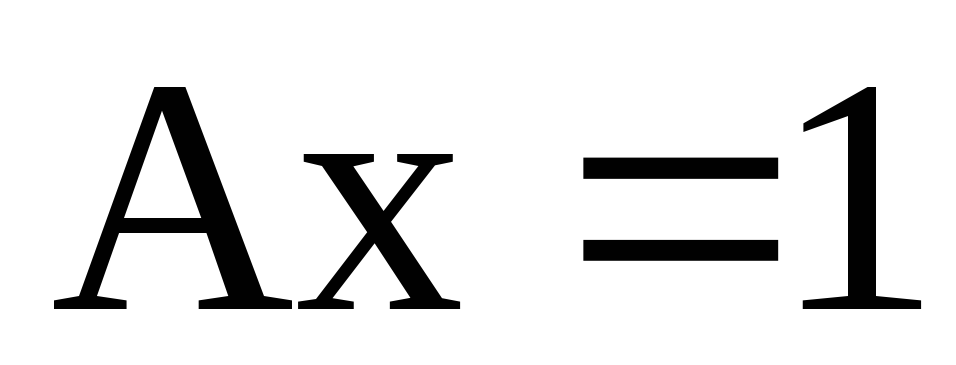 ;
г)
;
г)
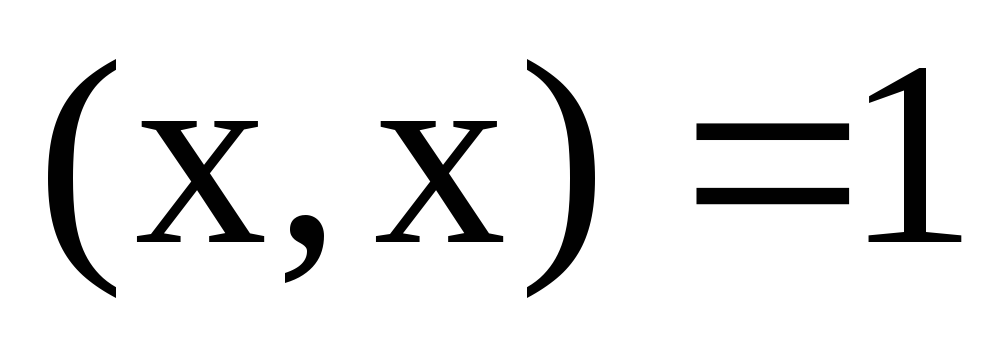 ?
? -
Нехай В(х,х)- квадратична форма, В(х,у)- полярна до неї білінійна форма, а А- самоспряжений лінійний оператор, який пов’язаний з білінійною формою співвідношенням (Ах,у)=В(х,у). Запишіть формулою як задається квадратична форма у власному ортонормованому базисі самоспряженого лінійного оператора А.
-
Нехай В(х,х)- квадратична форма, В(х,у)- полярна до неї білінійна форма, а А- самоспряжений лінійний оператор, який пов’язаний з білінійною формою співвідношенням (Ах,у)=В(х,у). Запишіть формулою як задається одинична сфера у власному ортонормованому базисі самоспряженого лінійного оператора А.
-
Сформулюйте теорему про стаціонарні значення квадратичної форми на одиничній сфері.
-
Чому дорівнюють стаціонарні значення квадратичної форми В(х,х) на одиничній сфері (на основі теореми)?
-
У яких точках досягаються стаціонарні значення квадратичної форми В(х,х) на одиничній сфері (на основі теореми)?
-
Для чого застосовується метод невизначених множників Лагранжа?
-
Яким методом ми досліджували екстремальні властивості квадратичної форми?
-
Сформулюйте принцип Релея.
-
Що дозволяє визначити принцип Релея?
-
Запишіть формулою чому дорівнює максимальне за модулем власне значення самоспряженого лінійного оператора (за принципом Релея).
-
Принцип Релея дозволяє знайти: а) найменше власне значення самоспряженого лінійного оператора; б) найменше за модулем власне значення самоспряженого лінійного оператора; в) найбільше власне значення самоспряженого лінійного оператора; г) найбільше за модулем власне значення самоспряженого лінійного оператора.
-
Дайте визначення визначника Грама системи векторів.
-
Як позначається визначник Грама системи векторів?
-
Коли визначник Грама системи векторів дорівнює нулю?
-
Визначники Грама яких наступних систем векторів дорівнюють нулю: а) лінійно незалежна; б) лінійно залежна; в) ортонормована; г) повна?
-
Коли визначник Грама системи векторів не дорівнює нулю?
-
Які значення може приймати визначник Грама лінійно незалежної системи векторів?
-
Визначник Грама лінійно незалежної системи векторів: а) менше нуля; б) дорівнює нулю; в) більше нуля; г) дорівнює одиниці.
-
Дайте визначення двох взаємних базисів.
-
Як позначаються взаємні базиси?
-
Дайте визначення символу Кронекера- Капеллі.
-
Як позначається символ Кронекера- Капеллі?
-
Скільки компонентів має символ Кронекера- Капеллі в n- вимірному лінійному просторі?
-
Як знайти базис, взаємний до ортонормованого?
-
Як позначаються коваріантні координати вектора?
-
Як позначаються контраваріантні координати вектора?
-
Запишіть формулу розкладання довільного вектора за його коваріантними координатами.
-
Запишіть формулу розкладання довільного вектора за його контраваріантними координатами.
-
Яка домовленість існує про індекси сумування в тензорній алгебрі при роботі з довільними базисами?
-
Які з наступних добутків тензорів є коректними з точки зору домовленості про сумування: а)
 ;
б)
;
б)
 ;
в)
;
в)
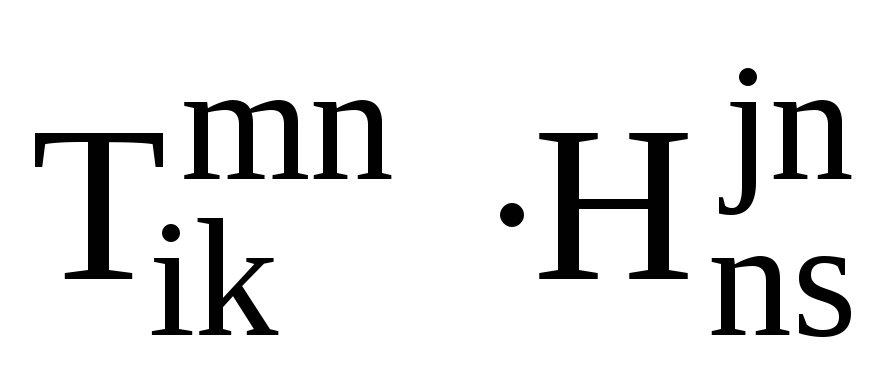 ;
г)
;
г)
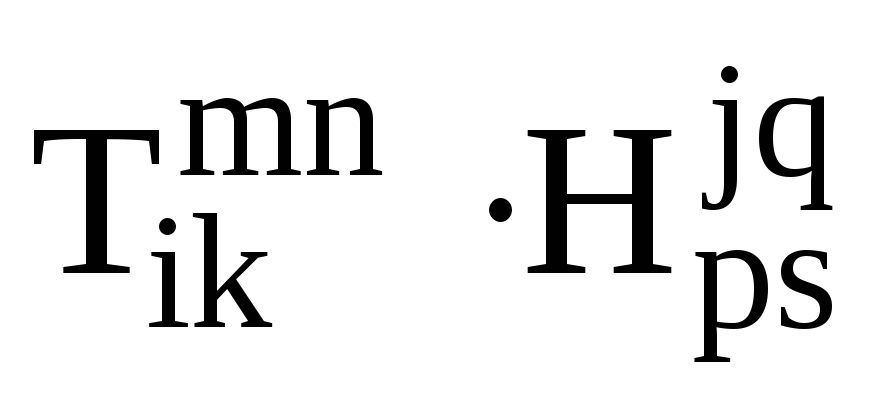 .
. -
Запишіть формули Гіббса.
-
Виходячи з формул Гіббса, запишіть як можна обчислити коваріантні координати вектора.
-
Виходячи з формул Гіббса, запишіть як можна обчислити контраваріантні координати вектора.
-
Підставивши у формули Гіббса базисні вектори, запишіть дві формули зв’язку між взаємними базисами.
-
Запишіть через матрицю
 зв’язок між взаємними базисами.
зв’язок між взаємними базисами. -
Запишіть через матрицю
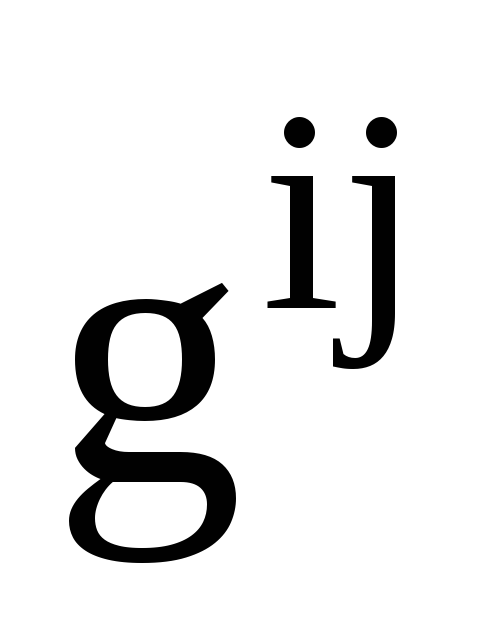 зв’язок між взаємними базисами.
зв’язок між взаємними базисами. -
Як визначаються елементи матриці
 ,
яка пов’язує два взаємні базиси?
,
яка пов’язує два взаємні базиси? -
Як визначаються елементи матриці
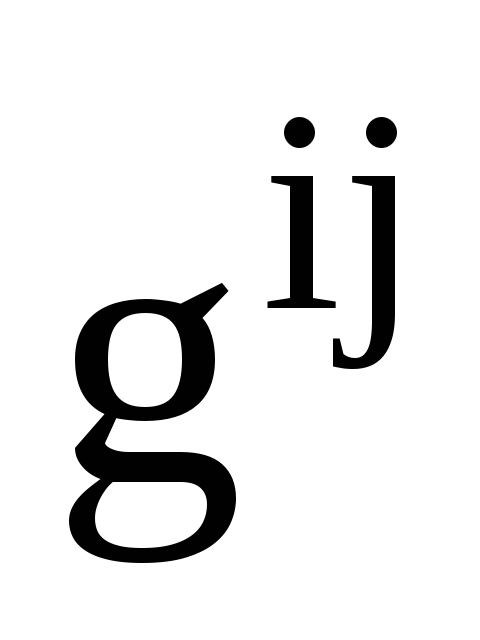 ,
яка пов’язує два взаємні базиси?
,
яка пов’язує два взаємні базиси? -
Запишіть формулою добуток матриць
 та
та
 ,
яка показує, що ці матриці взаємнообернені.
,
яка показує, що ці матриці взаємнообернені. -
Нехай
 ,
,
 та
та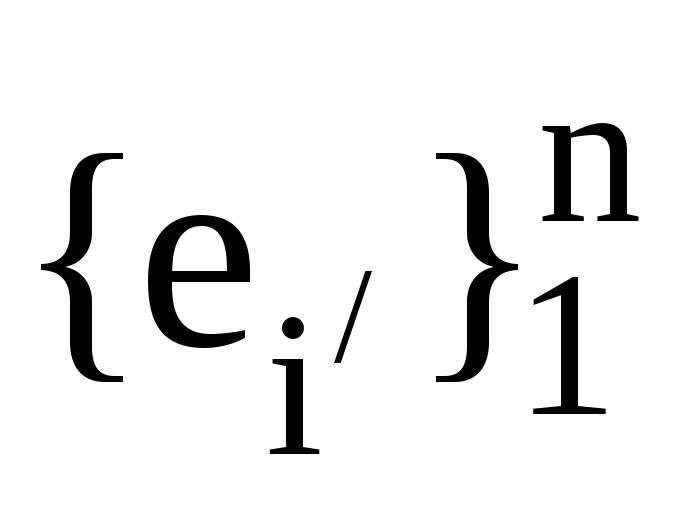 ,
, -
дві пари взаємних базисів. Також нехай
матриці g описують зв’язок між взаємними
базисами, а матриці b описують перехід
між парами взаємних базисів. Тоді
запишіть формулою зв’язок між базисами
-
дві пари взаємних базисів. Також нехай
матриці g описують зв’язок між взаємними
базисами, а матриці b описують перехід
між парами взаємних базисів. Тоді
запишіть формулою зв’язок між базисами
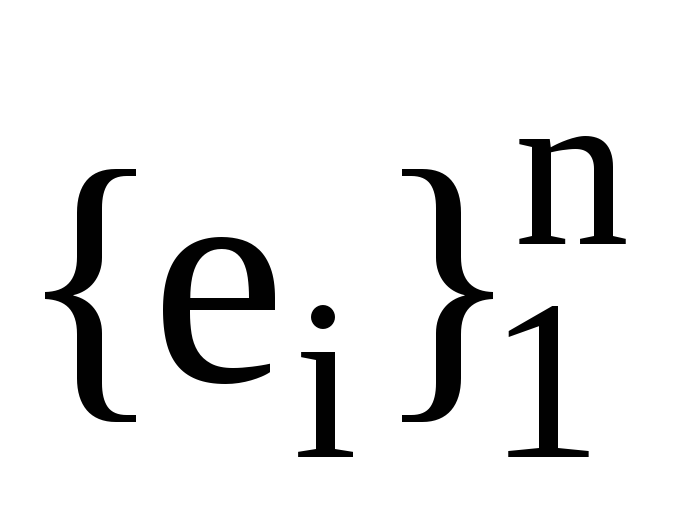 та
та
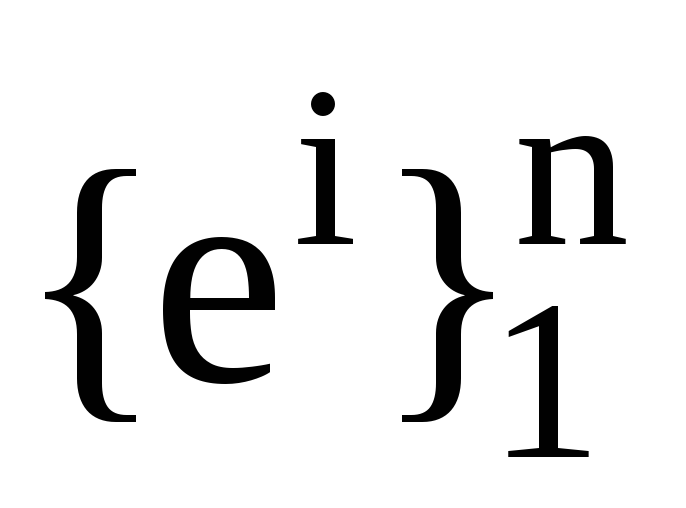 .
. -
Нехай
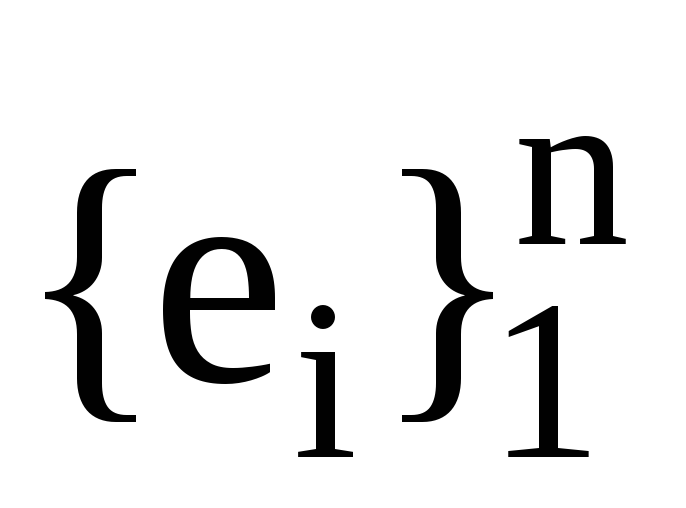 ,
,
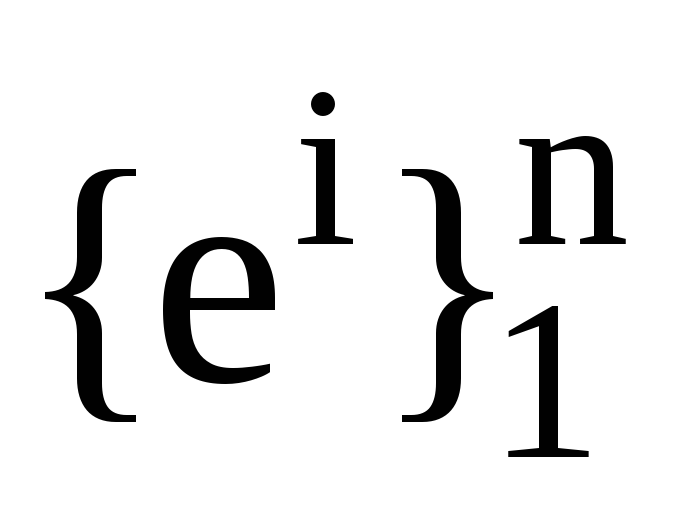 та
та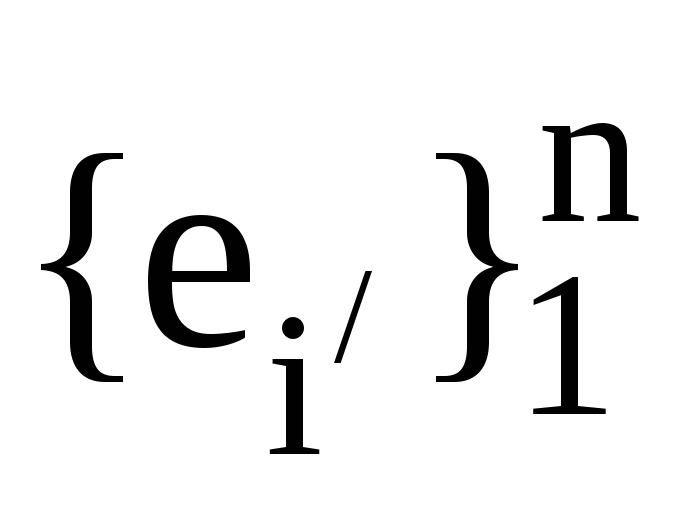 ,
,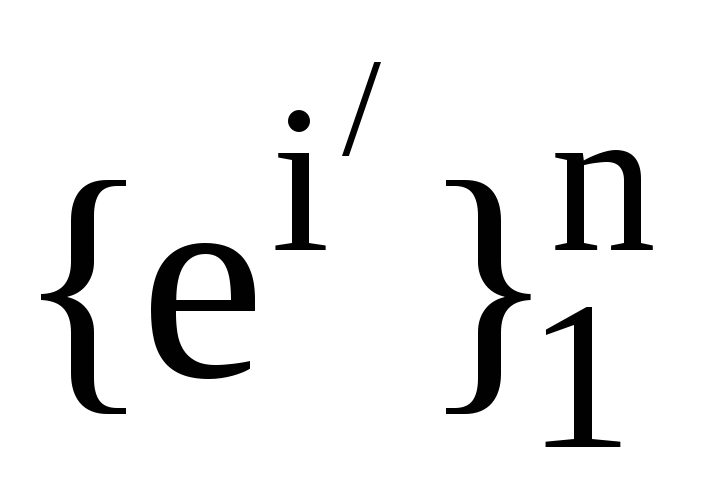 -
дві пари взаємних базисів. Також нехай
матриці g описують зв’язок між взаємними
базисами, а матриці b описують перехід
між парами взаємних базисів. Тоді
запишіть формулою зв’язок між базисами
-
дві пари взаємних базисів. Також нехай
матриці g описують зв’язок між взаємними
базисами, а матриці b описують перехід
між парами взаємних базисів. Тоді
запишіть формулою зв’язок між базисами
 та
та
 .
. -
Нехай
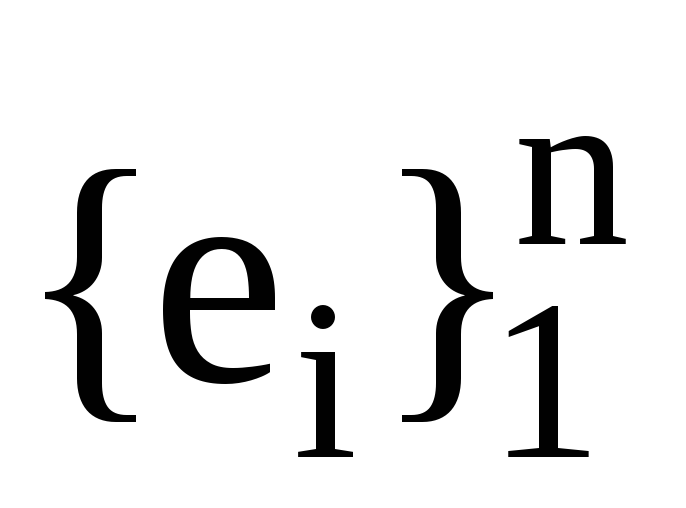 ,
,
 та
та ,
,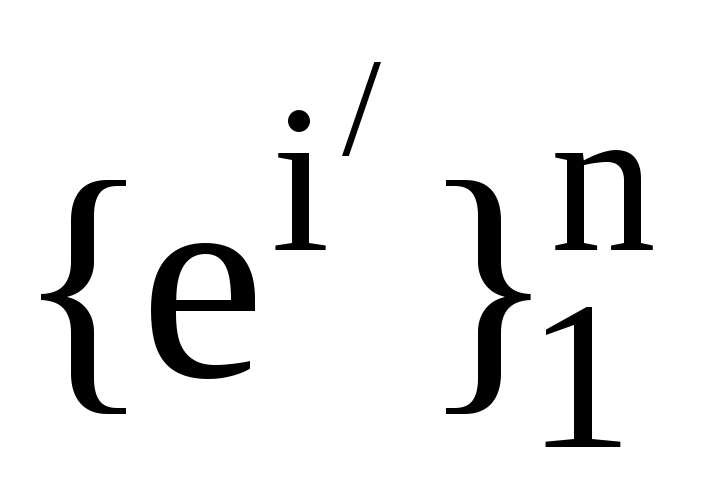 -
дві пари взаємних базисів. Також нехай
матриці g описують зв’язок між взаємними
базисами, а матриці b описують перехід
між парами взаємних базисів. Тоді
запишіть формулою зв’язок між базисами
-
дві пари взаємних базисів. Також нехай
матриці g описують зв’язок між взаємними
базисами, а матриці b описують перехід
між парами взаємних базисів. Тоді
запишіть формулою зв’язок між базисами
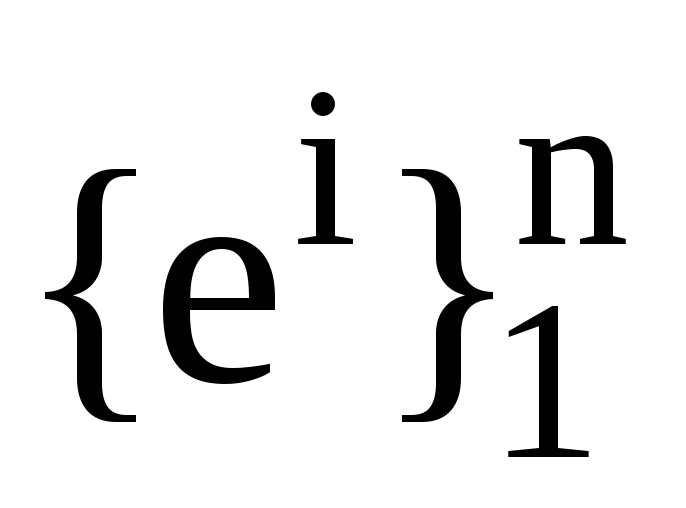 та
та
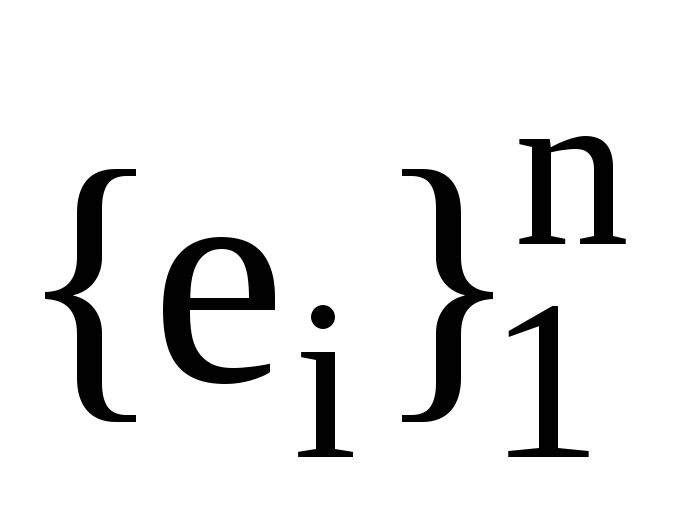 .
. -
Нехай
 ,
,
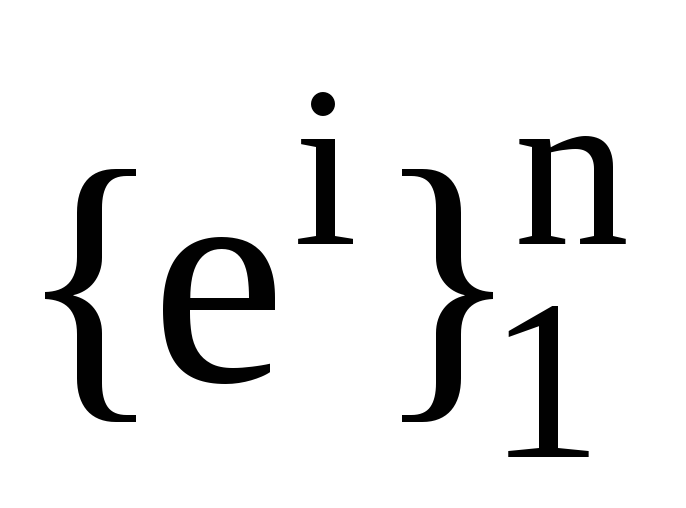 та
та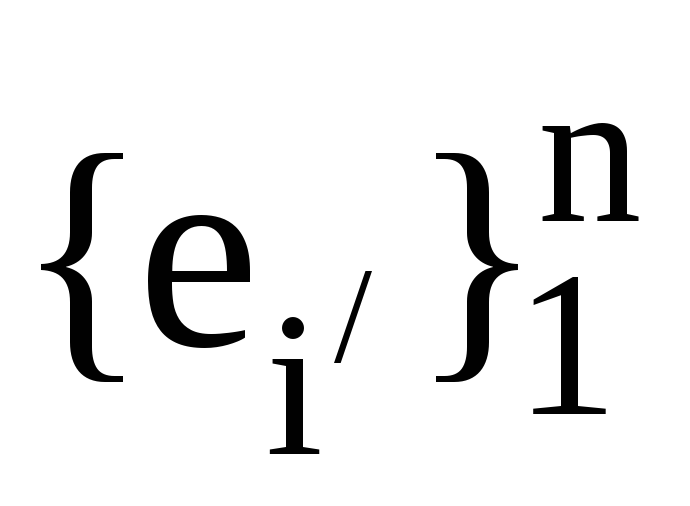 ,
, -
дві пари взаємних базисів. Також нехай
матриці g описують зв’язок між взаємними
базисами, а матриці b описують перехід
між парами взаємних базисів. Тоді
запишіть формулою зв’язок між базисами
-
дві пари взаємних базисів. Також нехай
матриці g описують зв’язок між взаємними
базисами, а матриці b описують перехід
між парами взаємних базисів. Тоді
запишіть формулою зв’язок між базисами
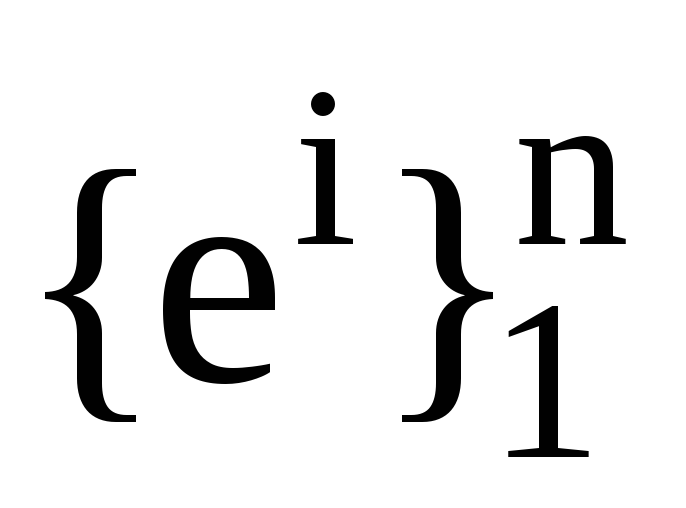 та
та
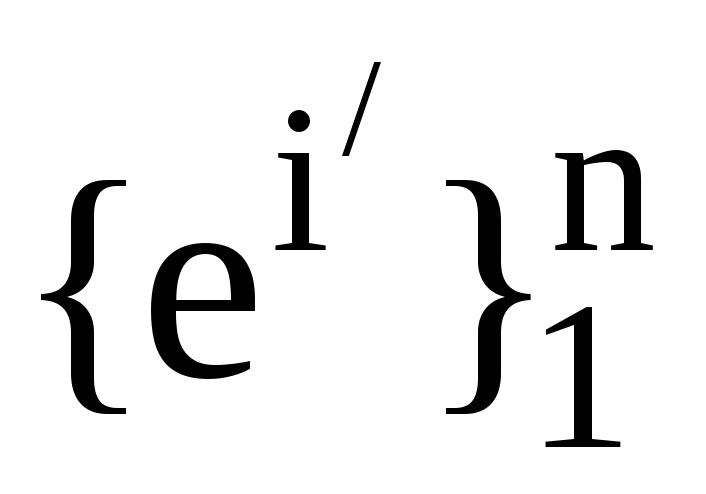 .
. -
Нехай
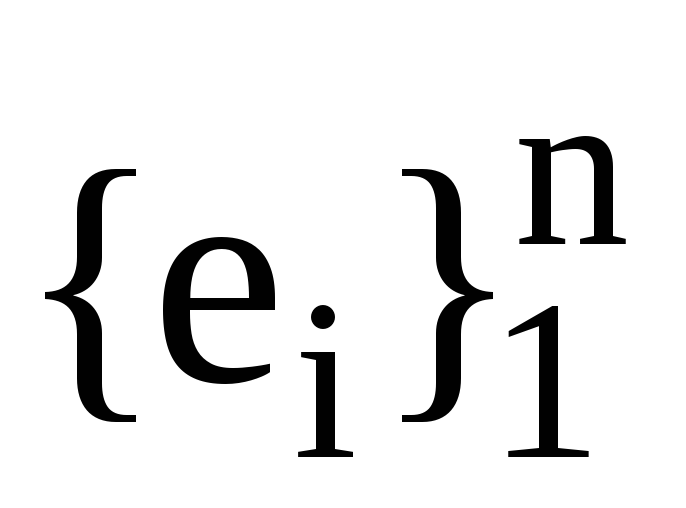 ,
,
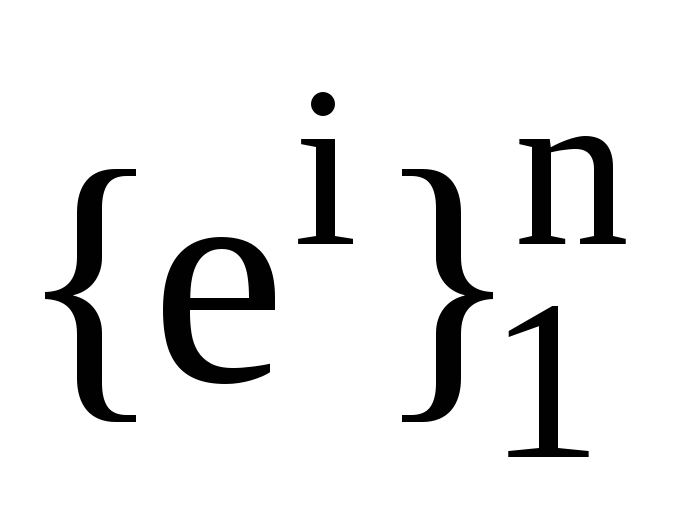 та
та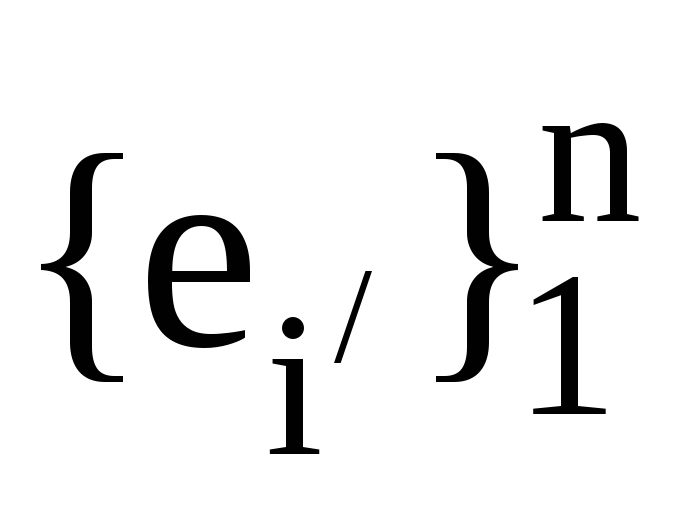 ,
,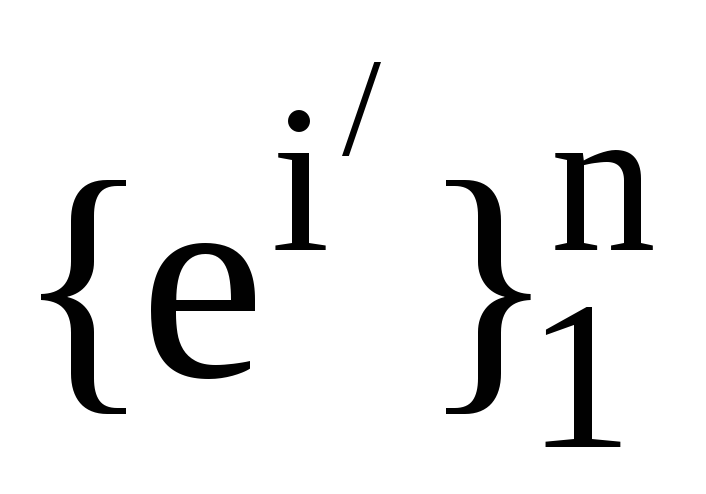 -
дві пари взаємних базисів. Також нехай
матриці g описують зв’язок між взаємними
базисами, а матриці b описують перехід
між парами взаємних базисів. Тоді
запишіть формулою зв’язок між базисами
-
дві пари взаємних базисів. Також нехай
матриці g описують зв’язок між взаємними
базисами, а матриці b описують перехід
між парами взаємних базисів. Тоді
запишіть формулою зв’язок між базисами
 та
та
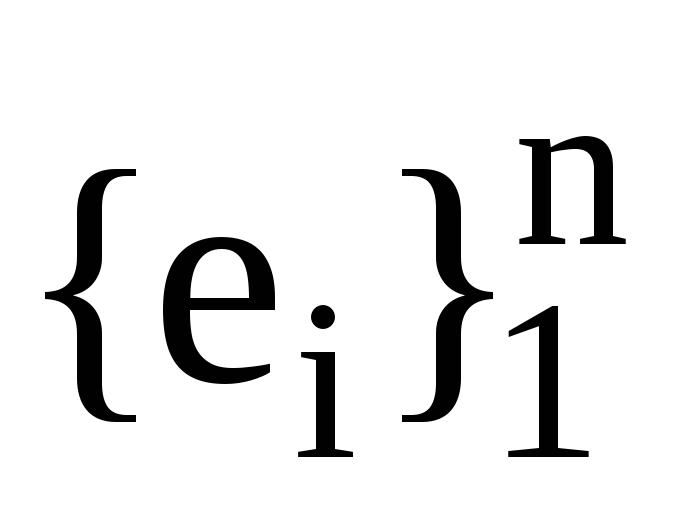 .
. -
Нехай
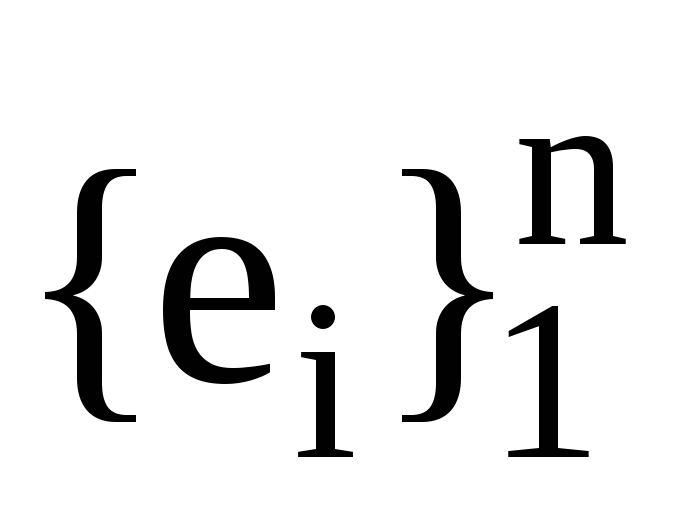 ,
,
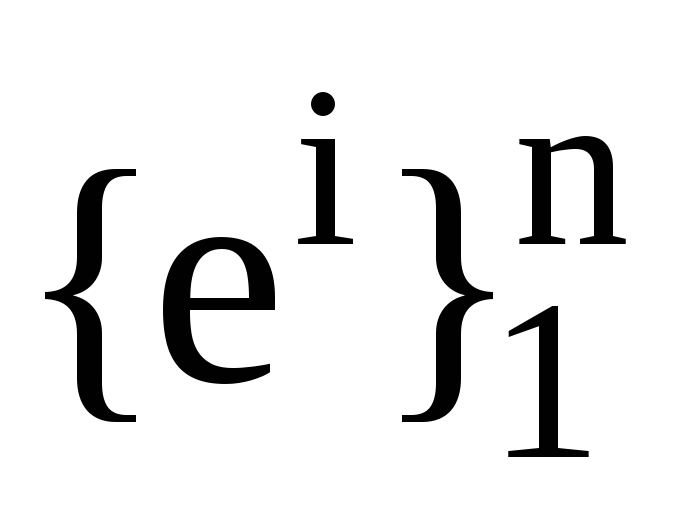 та
та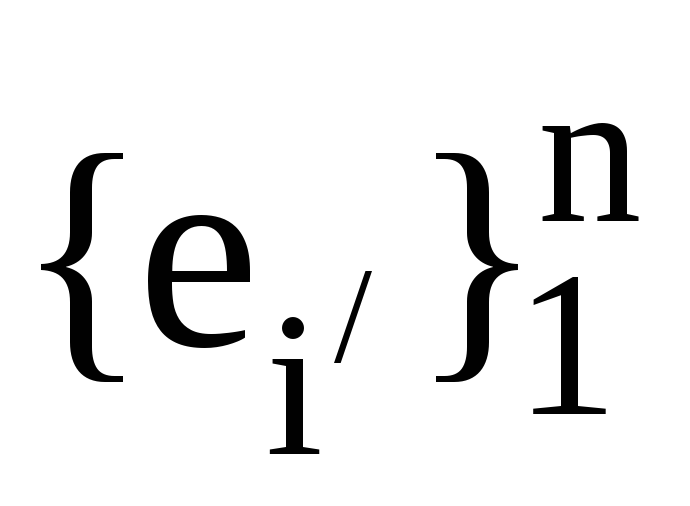 ,
, -
дві пари взаємних базисів. Також нехай
матриці g описують зв’язок між взаємними
базисами, а матриці b описують перехід
між парами взаємних базисів. Тоді
запишіть формулою зв’язок між базисами
-
дві пари взаємних базисів. Також нехай
матриці g описують зв’язок між взаємними
базисами, а матриці b описують перехід
між парами взаємних базисів. Тоді
запишіть формулою зв’язок між базисами
 та
та
 .
. -
Нехай
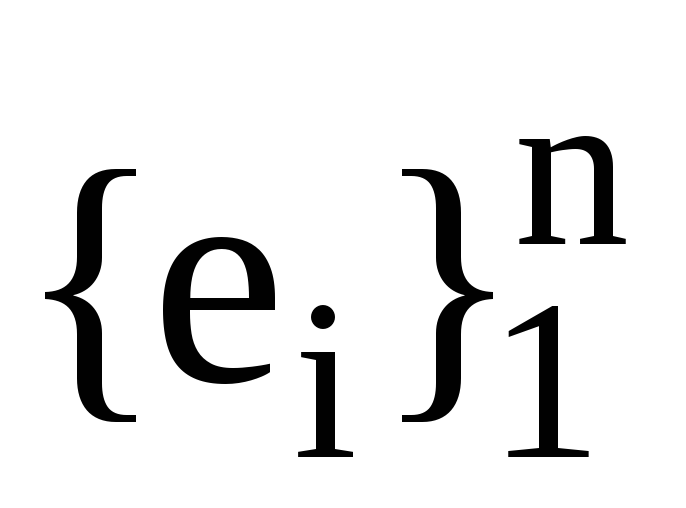 ,
,
 та
та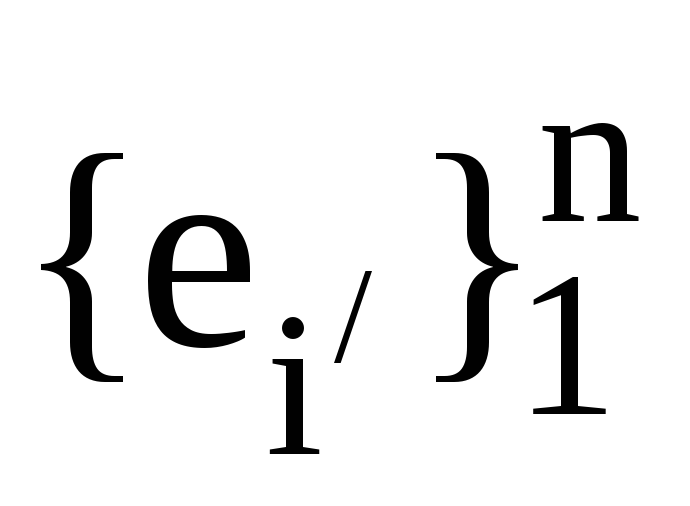 ,
, -
дві пари взаємних базисів. Також нехай
-
дві пари взаємних базисів. Також нехай
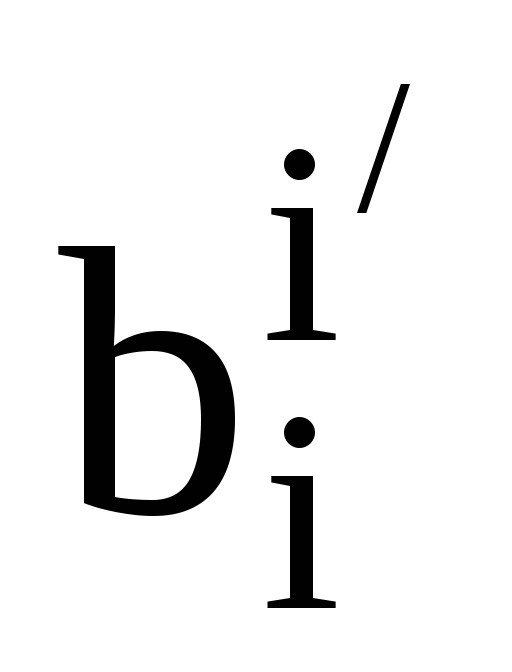 та
та
 -
матриці переходу між цими базисами.
Запишіть формулами два переходи, які
задає матриця
-
матриці переходу між цими базисами.
Запишіть формулами два переходи, які
задає матриця
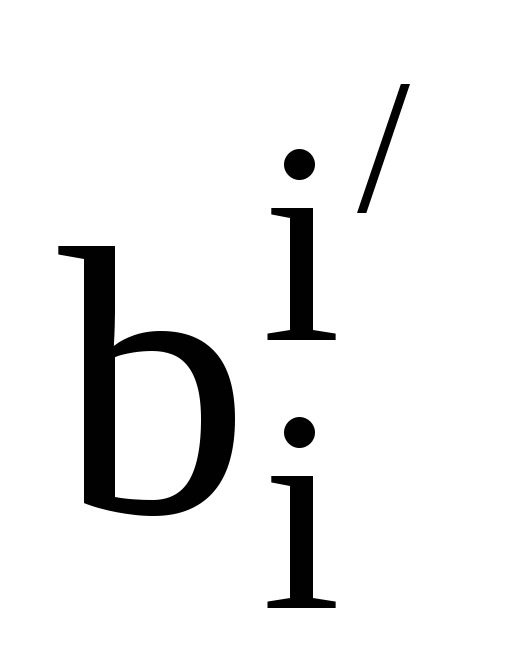 .
. -
Нехай
 ,
,
 та
та ,
,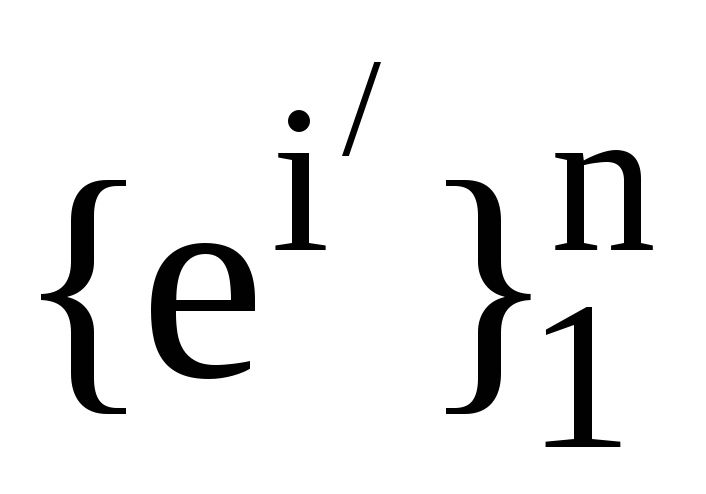 -
дві пари взаємних базисів. Також нехай
-
дві пари взаємних базисів. Також нехай
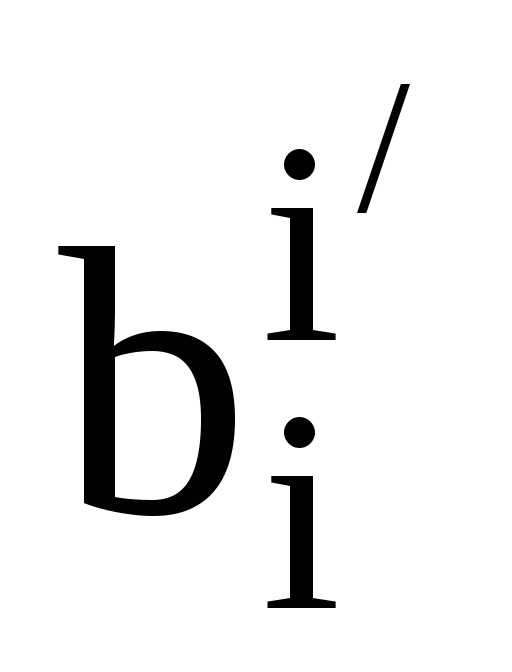 та
та
 -
матриці переходу між цими базисами.
Запишіть формулами два переходи, які
задає матриця
-
матриці переходу між цими базисами.
Запишіть формулами два переходи, які
задає матриця
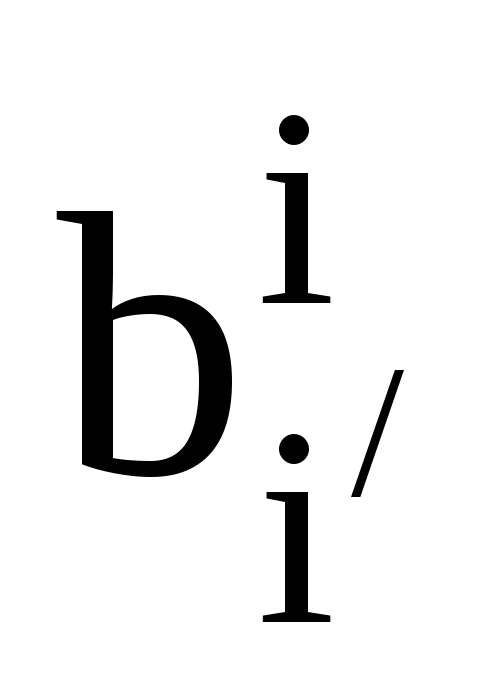 .
. -
Яка з двох матриць переходу
 та
та
 описує прямий перехід, а яка обернений?
описує прямий перехід, а яка обернений? -
Нехай
 ,
,
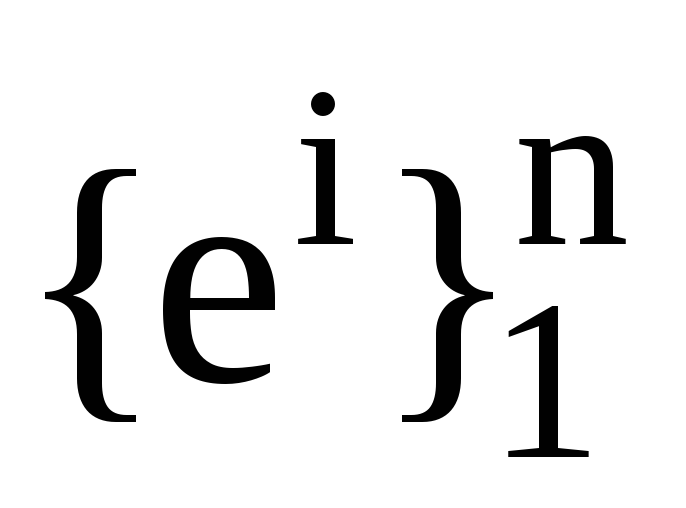 та
та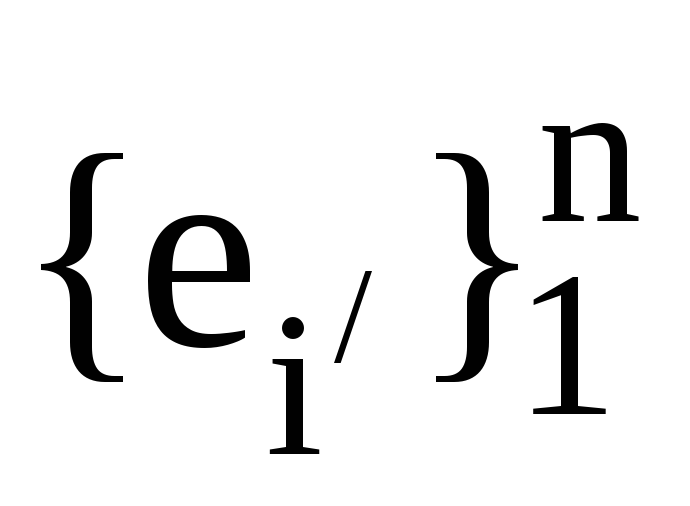 ,
,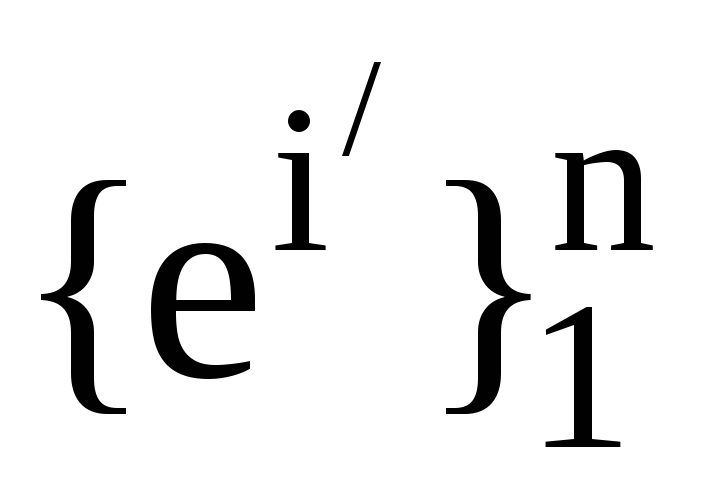 -
дві пари взаємних базисів. Запишіть
через скалярній добуток як визначаються
елементи матриці
-
дві пари взаємних базисів. Запишіть
через скалярній добуток як визначаються
елементи матриці
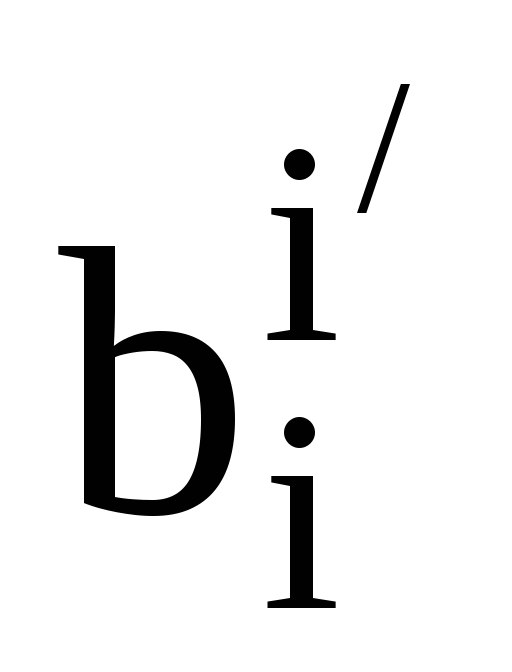 .
. -
Нехай
 ,
,
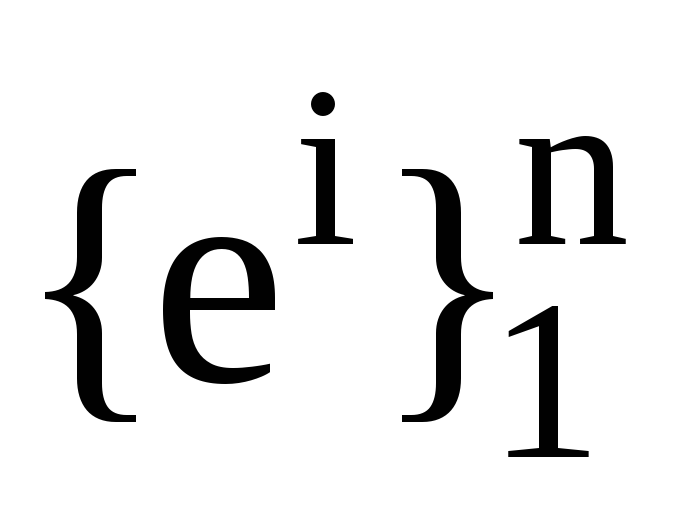 та
та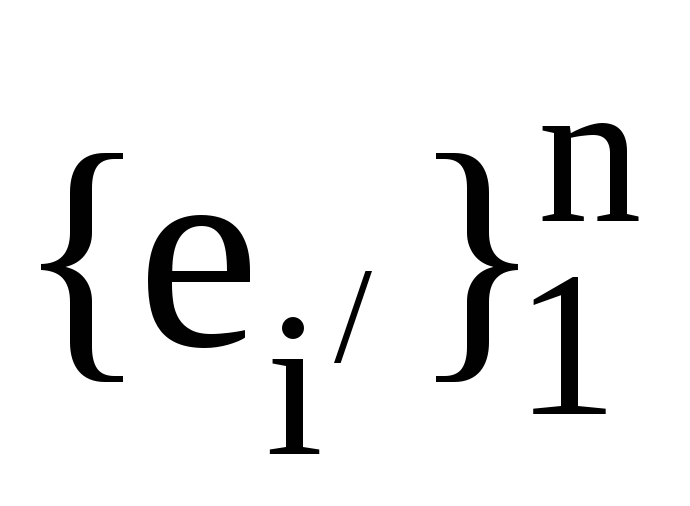 ,
,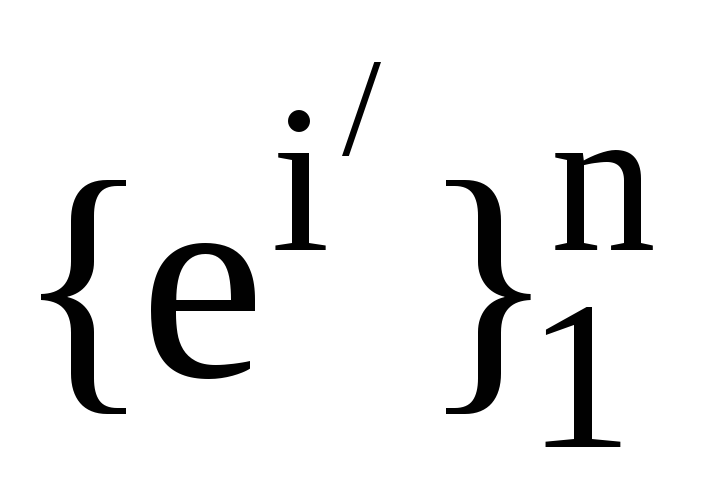 -
дві пари взаємних базисів. Запишіть
через скалярній добуток як визначаються
елементи матриці
-
дві пари взаємних базисів. Запишіть
через скалярній добуток як визначаються
елементи матриці
 .
. -
Нехай
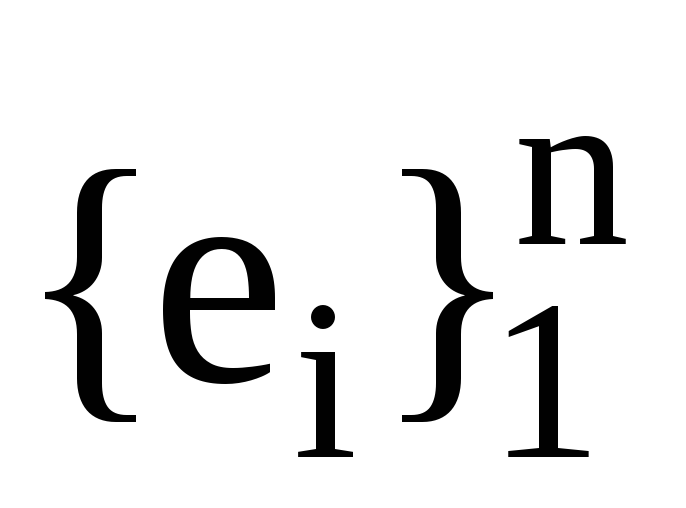 ,
,
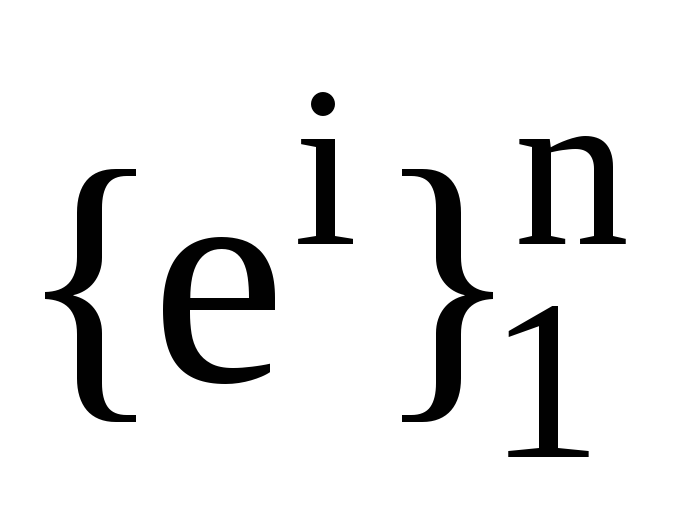 та
та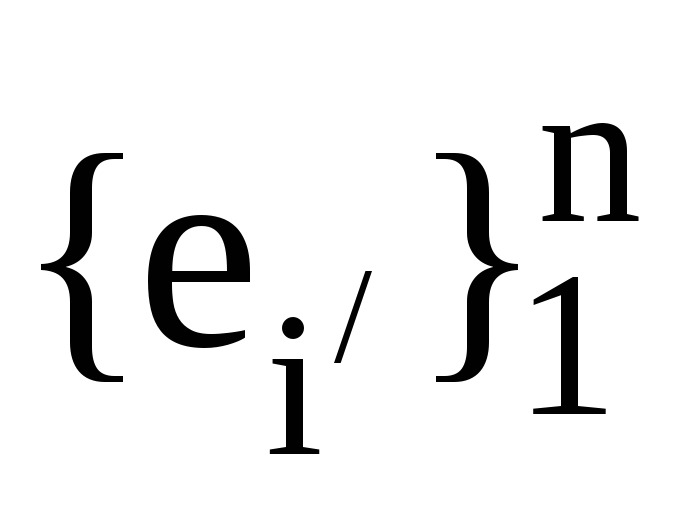 ,
, -
дві пари взаємних базисів. Запишіть
чотири формули переходу між цими
базисами за допомогою матриці переходу
b.
-
дві пари взаємних базисів. Запишіть
чотири формули переходу між цими
базисами за допомогою матриці переходу
b. -
Нехай
 ,
,
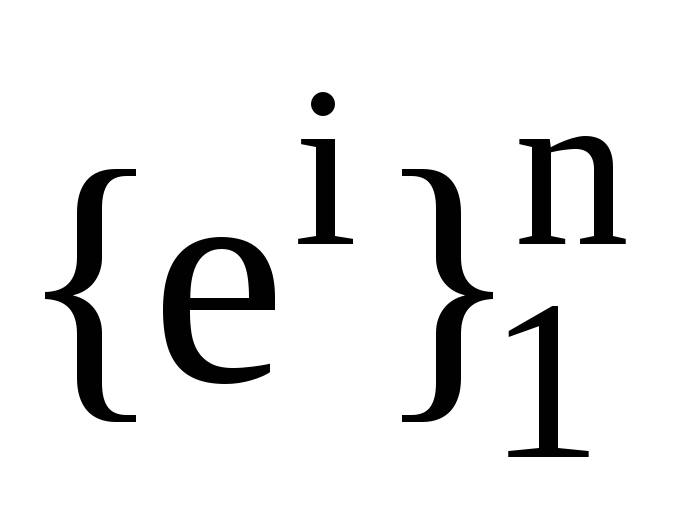 та
та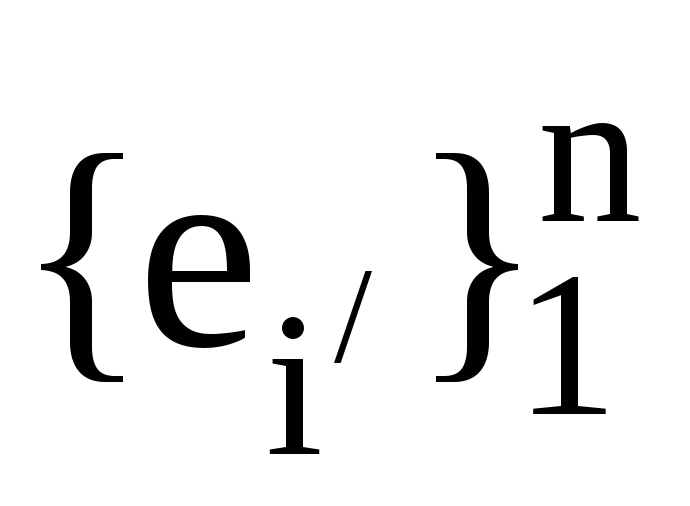 ,
,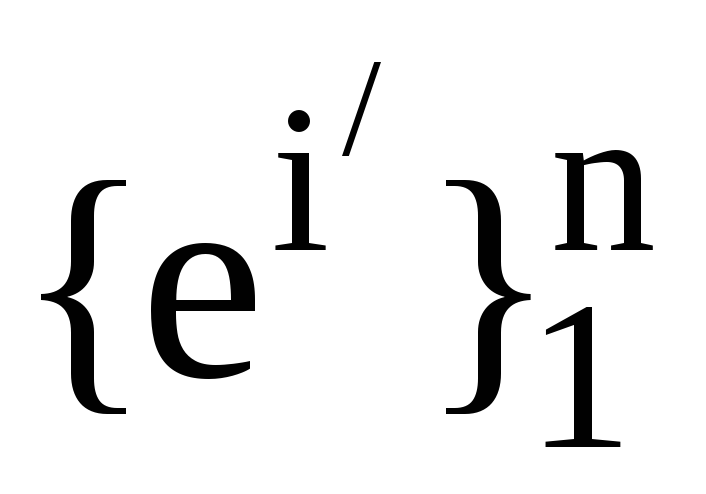 -
дві пари взаємних базисів. Також нехай
-
дві пари взаємних базисів. Також нехай
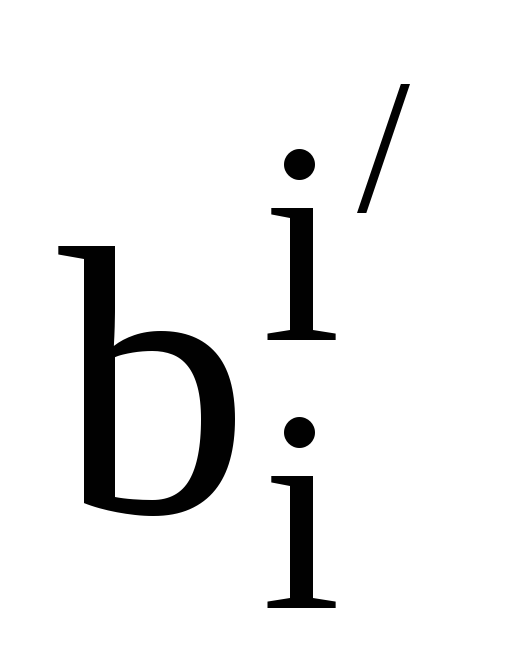 та
та
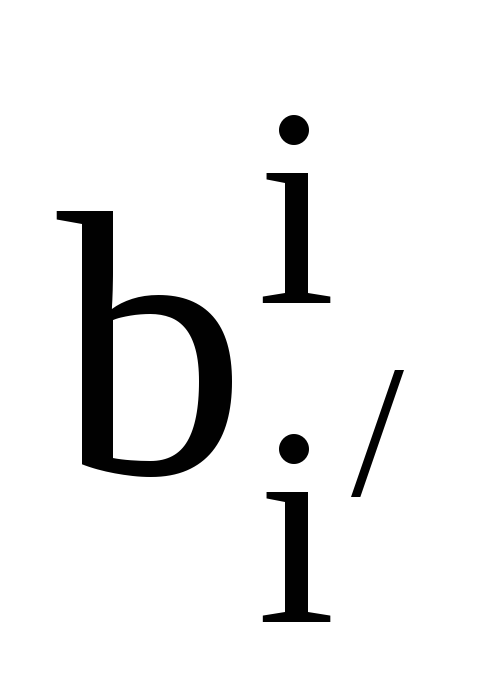 -
матриці переходу між цими базисами.
Запишіть формулу перетворення
коваріантних координат вектора.
-
матриці переходу між цими базисами.
Запишіть формулу перетворення
коваріантних координат вектора. -
Нехай
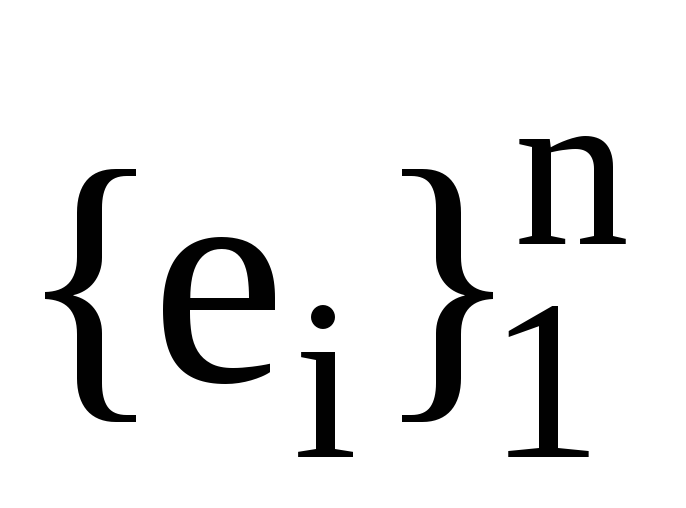 ,
,
 та
та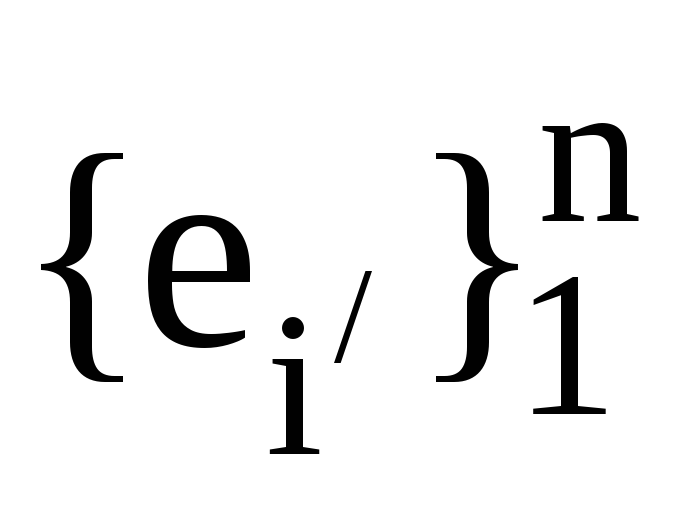 ,
,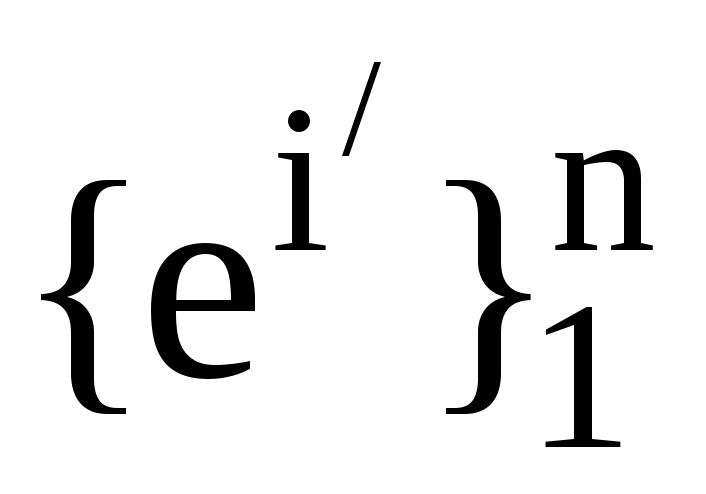 -
дві пари взаємних базисів. Також нехай
-
дві пари взаємних базисів. Також нехай
 та
та
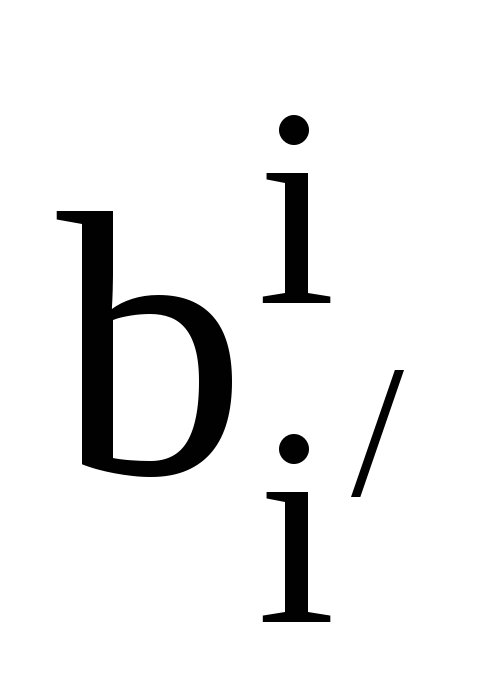 -
матриці переходу між цими базисами.
Запишіть формулу перетворення
контраваріантних координат вектора.
-
матриці переходу між цими базисами.
Запишіть формулу перетворення
контраваріантних координат вектора. -
Дайте визначення коваріантних координат вектора.
-
Дайте визначення контраваріантних координат вектора.
-
Дайте визначення тензора у довільному базисі.
-
Які позначення використовуються для тензорів при визначенні у довільному базисі?
-
Запишіть формулу перетворення тензора при переході до нового базису.
-
Скільки координат має тензор типу (р,q) у лінійному просторі розмірності n?
-
Якщо тензор типу (р,q), то що позначають числа p та q?
-
Дайте визначення рангу тензора.
-
Які індекси називаються коваріантними?
-
Які індекси називаються контраваріантними?
-
Запишіть формулу, яка дозволяє вектор розглядати як тензор першого рангу один раз коваріантний.
-
Запишіть формулу, яка дозволяє вектор розглядати як тензор першого рангу один раз контраваріантний.
-
Охарактеризуєте скаляр з точки зору тензорних властивостей.
-
Дайте визначення нуль- тензора.
-
Охарактеризуйте символ Кронекера- Капеллі з точки зору тензорних властивостей.
-
Тензором якого типу є символ Кронекера- Капеллі?
-
Тензором якого типу є матриця білінійної форми?
-
Тензором якого типу є матриця лінійного оператора?
-
Дайте визначення операції додавання тензорів.
-
Дайте визначення операції множення тензора на число.
-
Дайте визначення операції множення тензорів.
-
Дайте визначення операції звертання тензора за парою індексів.
-
Дайте визначення операції множення тензорів з наступним звертанням за парою індексів.
-
Дайте визначення операції симетрування тензора за парою індексів.
-
Дайте визначення операції альтернування тензора за парою індексів.
-
Як пов’язані між собою коваріантні та контраваріантні координати вектора в ортонормованому базисі?
-
Запишіть аналог формул Гіббса в ортонормованому базисі.
-
Сформулюйте домовленість про сумування за індексами для тензорних виразів в ортонормованих базисах.
-
Нехай (
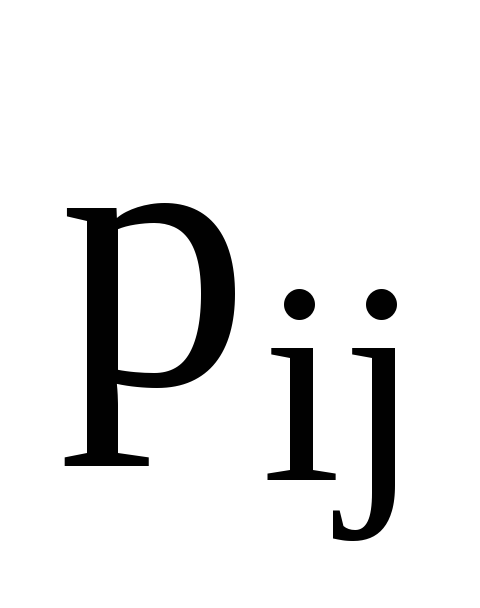 )-
матриця переходу від базису
)-
матриця переходу від базису
 до базису
до базису
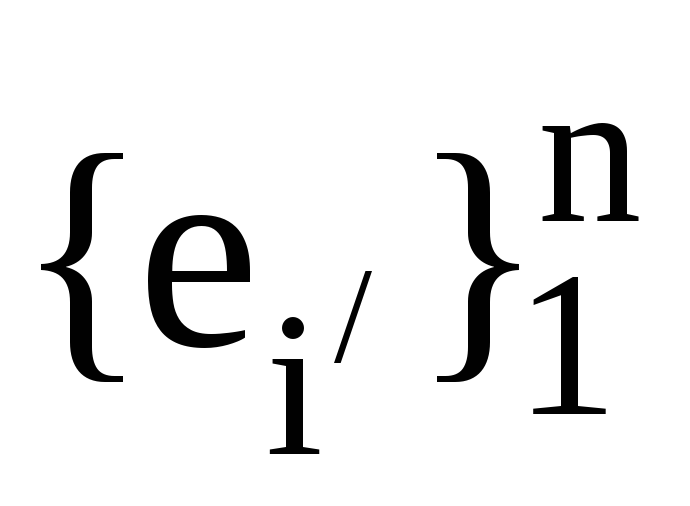 .
Тоді запишіть формулою як вектори
.
Тоді запишіть формулою як вектори
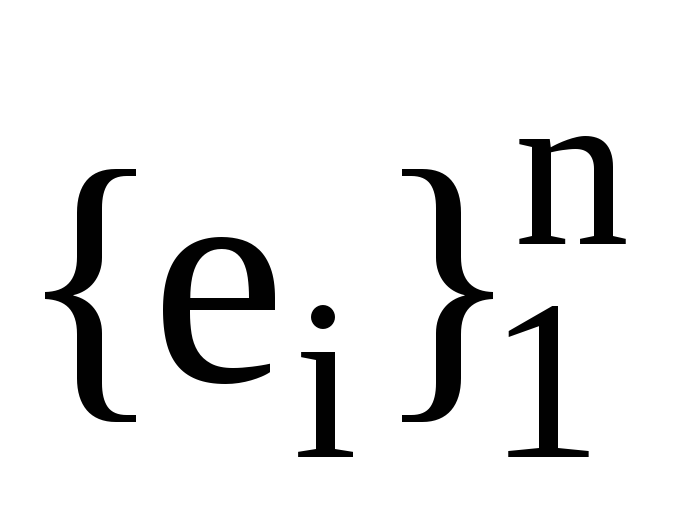 виражаються через вектори
виражаються через вектори
 .
. -
Нехай (
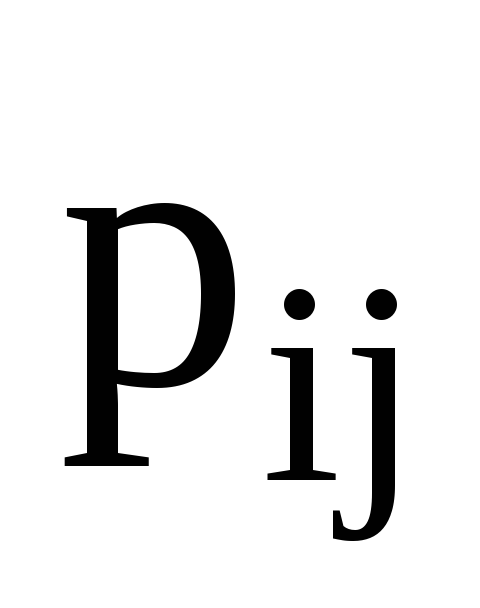 )-
матриця переходу від ортонормованого
базису
)-
матриця переходу від ортонормованого
базису
 до ортонормованого базису
до ортонормованого базису
 .
Тоді запишіть формулою як вектори
.
Тоді запишіть формулою як вектори
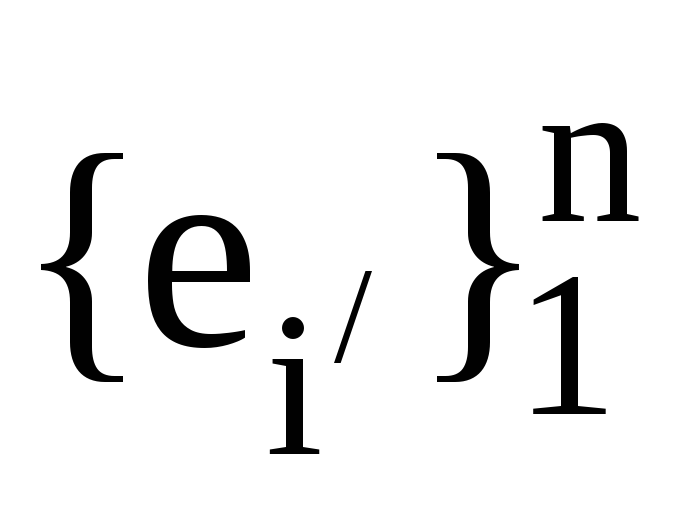 виражаються через вектори
виражаються через вектори
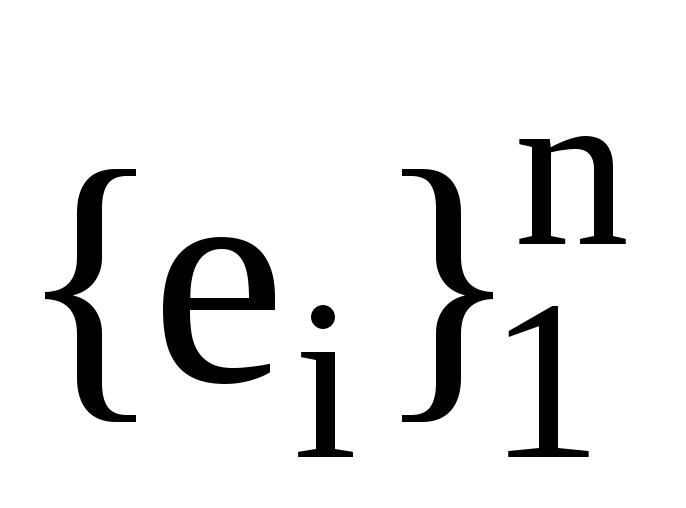 .
. -
Нехай (
 )-
матриця переходу від ортонормованого
базису
)-
матриця переходу від ортонормованого
базису
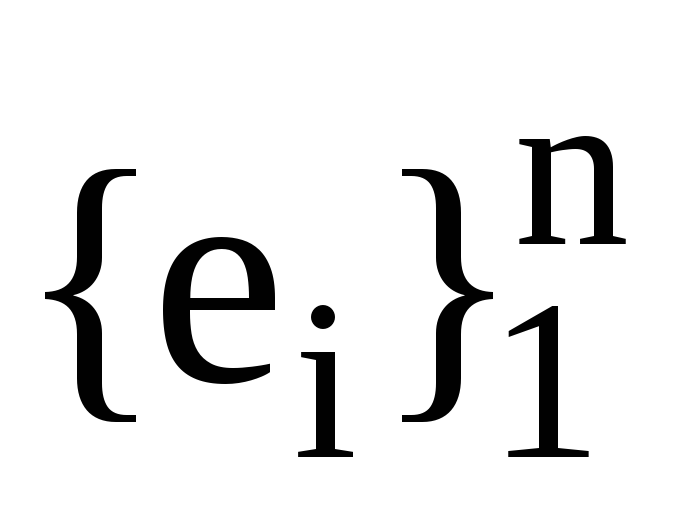 до ортонормованого базису
до ортонормованого базису
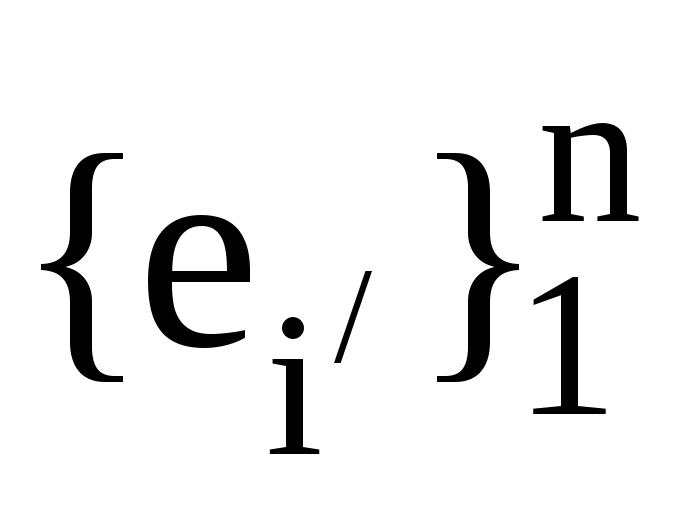 ,
а (
,
а ( )-
матриця переходу від ортонормованого
базису
)-
матриця переходу від ортонормованого
базису
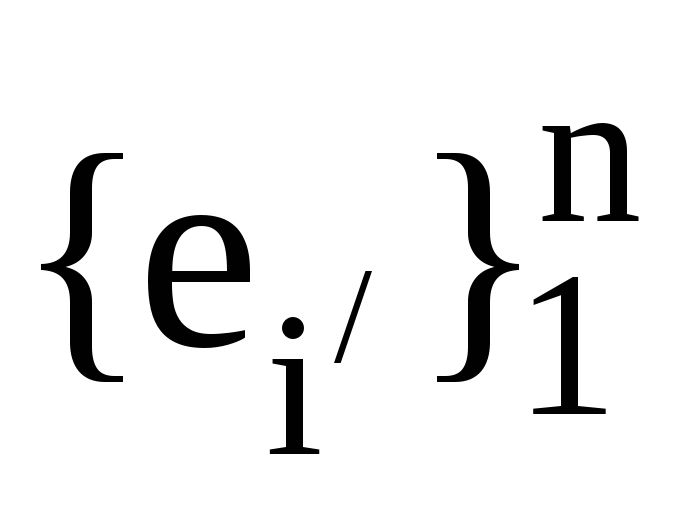 до ортонормованого базису
до ортонормованого базису
 .
Яким співвідношенням пов’язані елементи
матриць
.
Яким співвідношенням пов’язані елементи
матриць
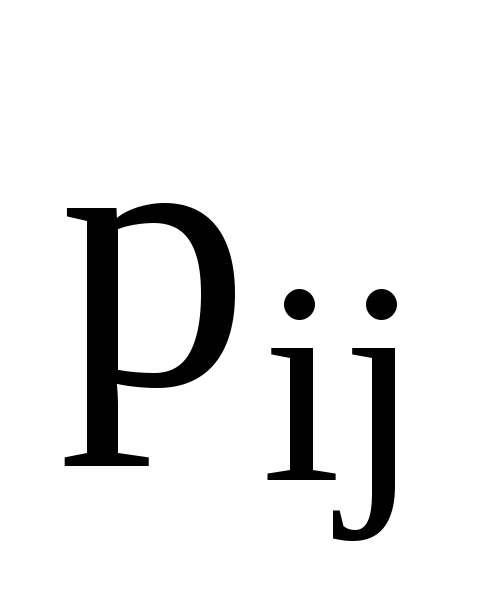 та
та
 ?
? -
Нехай (
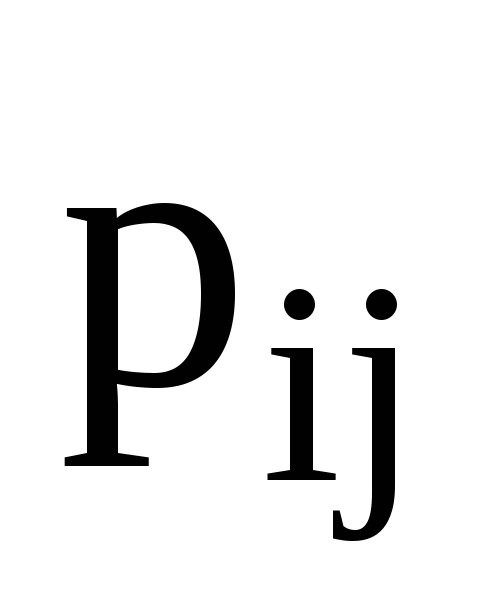 )-
матриця переходу від ортонормованого
базису
)-
матриця переходу від ортонормованого
базису
 до ортонормованого базису
до ортонормованого базису
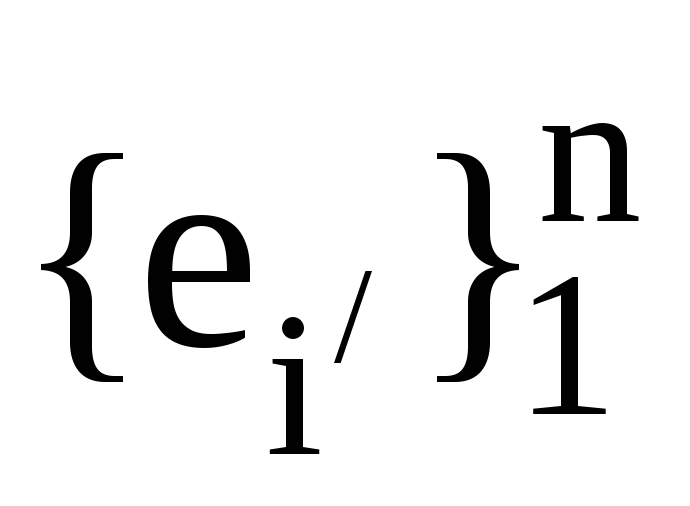 .
Якими властивостями характеризується
матриця (
.
Якими властивостями характеризується
матриця ( )?
)? -
Дайте визначення афінного ортогонального тензора r- го рангу в n- вимірному евклідовому просторі.
-
Скільки координат має афінний ортогональний тензор r- го рангу в n- вимірному евклідовому просторі?
-
Запишіть формулу перетворення тензора при переході з одного ортонормованого базису в інший.
-
Дайте визначення операції скалярного добутку тензорів.
-
Сформулюйте ознаку тензорності величини.
-
Який висновок про об’єкт дозволяє зробити ознака тензорності величини?
-
Якому визначенню еквівалентна ознака тензорності величини?
-
Дайте визначення абсолютно симетричного тензора r- го ранга.
-
Дайте визначення абсолютно антисиметричного тензора r- го ранга.
-
Скільки незалежних координат має абсолютно антисиметричний тензор 2- го рангу у тривимірному евклідовому просторі?
-
Скільки незалежних координат має абсолютно симетричний тензор 2- го рангу у тривимірному евклідовому просторі?
-
З точки зору геометричної інтерпретації який об’єкт може бути поставлений у відповідність абсолютно антисиметричному тензору 2- го рангу у тривимірному евклідовому просторі?
-
З точки зору геометричної інтерпретації який об’єкт може бути поставлений у відповідність абсолютно симетричному тензору 2- го рангу у тривимірному евклідовому просторі?
-
Якщо
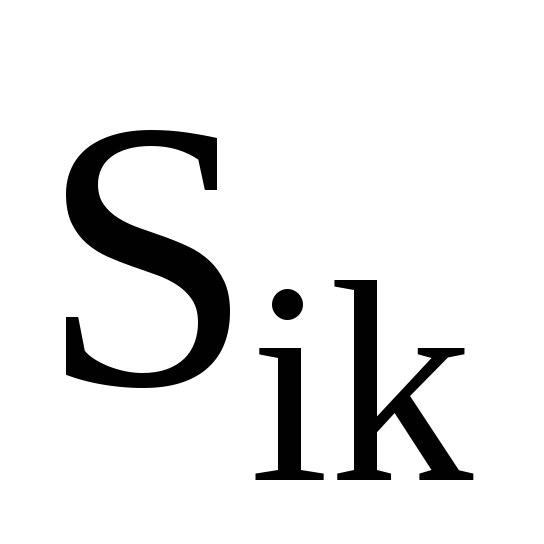 -
абсолютно симетричний тензор 2- го
рангу, а
-
абсолютно симетричний тензор 2- го
рангу, а
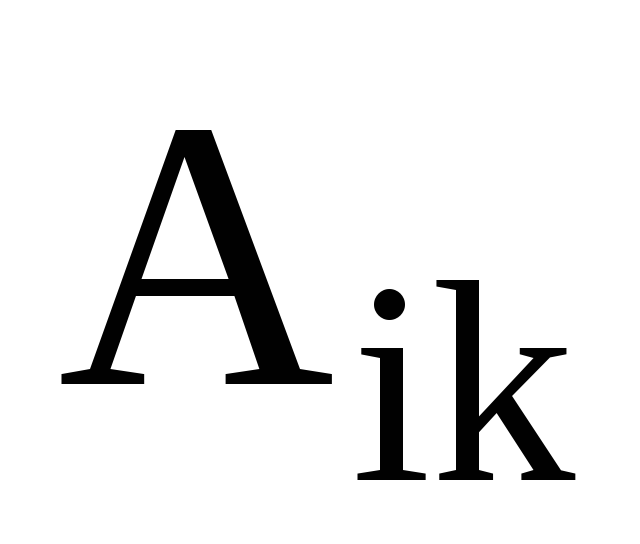 -
абсолютно антисиметричний тензор 2- го
рангу, то чому дорівнює добуток
-
абсолютно антисиметричний тензор 2- го
рангу, то чому дорівнює добуток
 ?
? -
Запишіть формули, за якими будь- який тензор 2- го рангу можна представити у вигляді суми симетричного та антисиметричного тензорів.
-
Дайте визначення власного ортогонального перетворення.
-
Дайте визначення невласного ортогонального перетворення.
-
Дайте визначення псевдотензора.
-
Як дізнатися є даний об’єкт істинним тензором чи псевдотензором?
-
Чи однаково перетворюються істинний тензор та псевдотензор при власному ортогональному перетворенні?
-
Чи однаково перетворюються істинний тензор та псевдотензор при невласному ортогональному перетворенні?
-
Чи є псевдотензором сума двох псевдотензорів?
-
Чи є псевдотензором добуток двох псевдотензорів?
-
Чи є псевдотензором добуток істинного тензора та псевдотензора?
-
Чи є псевдотензором звертання псевдотензора за парою індексів?
-
Наведіть приклад псевдотензора та аргументуйте його.
-
Символ Кронекера є тензором чи псевдотензором?
-
Символ Кронекера є абсолютно симетричним чи антисиметричним тензором?
-
Дайте визначення символу Леві- Чивіта.
-
Як позначається символ Леві- Чивіта?
-
Скільки компонентів має символ Леві- Чивіта?
-
Скільки нульових компонентів має символ Леві- Чивіта?
-
Скільки ненульових компонентів має символ Леві- Чивіта?
-
Символ Леві- Чивіта є тензором чи псевдотензором?
-
Символ Леві- Чивіта є абсолютно симетричним чи антисиметричним псевдотензором?
-
Символ Леві- Чивіта є псевдотензором якого рангу?
-
Запишіть векторний добуток векторів через символ Леві- Чивіта.
-
Розпишіть добуток
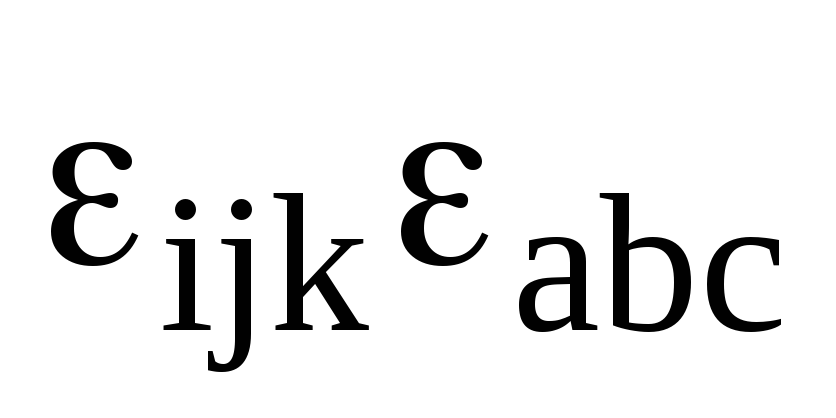 через символи Кронекера.
через символи Кронекера. -
Розпишіть добуток
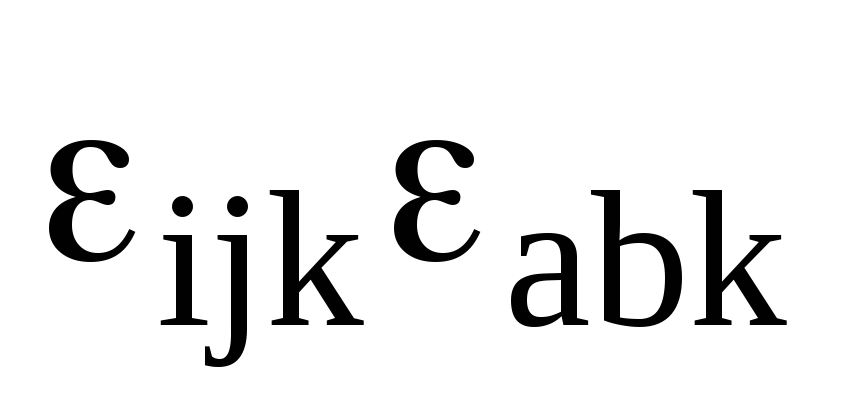 через символи Кронекера.
через символи Кронекера. -
Розпишіть добуток
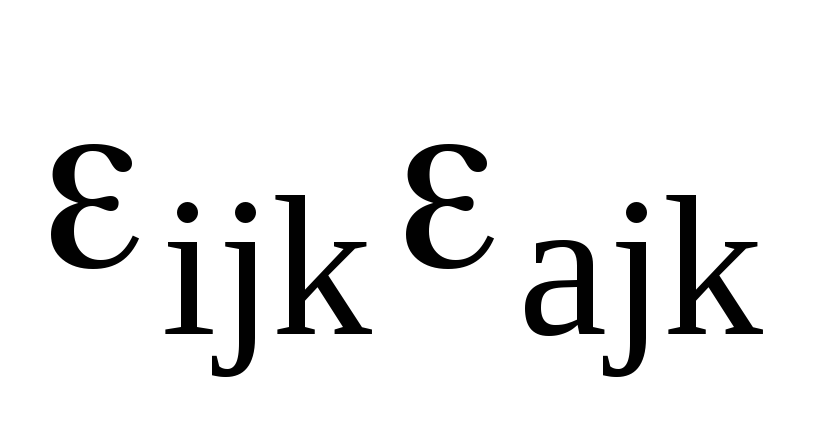 через символи Кронекера.
через символи Кронекера. -
Чому дорівнює добуток
 ?
? -
Як можна встановити співвідношення між тензорами 2- го рангу та матрицями лінійних операторів?
-
Як можна встановити співвідношення між тензорами 2- го рангу та скалярами?
-
Як можна ввести поняття оберненого тензора для тензора 2- го рангу?
-
Чому еквівалентна операція приведення тензора 2- го рангу до головних осей?
-
Дайте визначення тензорного поля.
-
Скільки функцій задають тензорне поле r- го рангу?
-
Що вивчає тензорний аналіз?
-
Дайте визначення операції диференціювання тензорного поля r- го рангу.
-
Скільки функцій буде отримано при диференціюванні тензорного поля r- го рангу?
-
Як змінює ранг тензорного поля операція диференціювання?
-
Нехай
 -
координати вектора х у старому
ортонормованому базисі, а
-
координати вектора х у старому
ортонормованому базисі, а
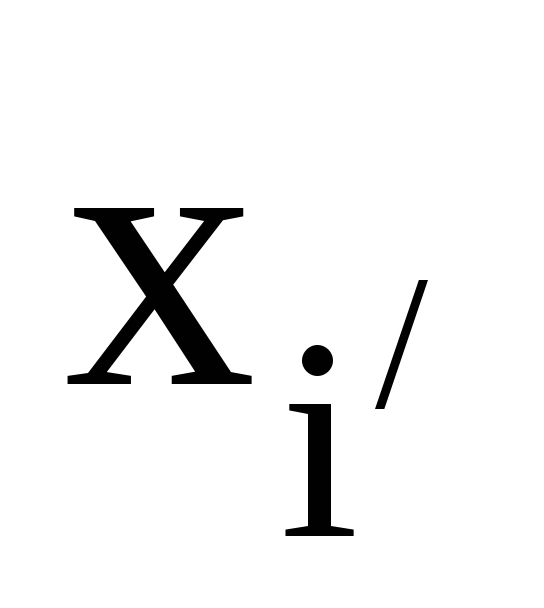 -
координати вектора х у новому
ортонормованому базисі. Тоді чому
дорівнює похідна
-
координати вектора х у новому
ортонормованому базисі. Тоді чому
дорівнює похідна
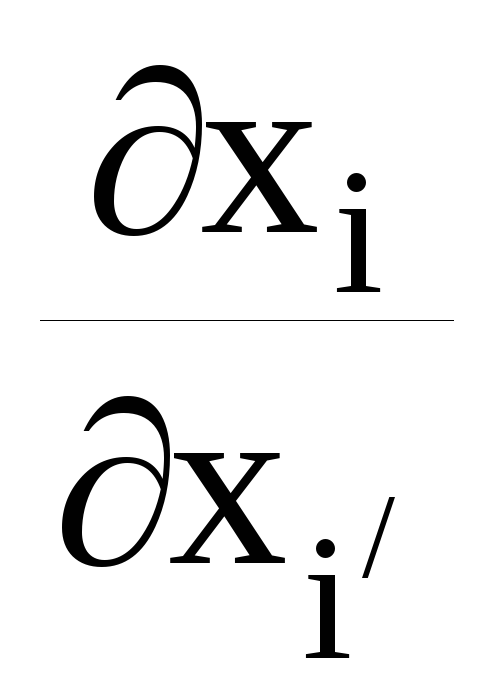 ?
? -
Дайте визначення операції градієнт тензорного поля.
-
Як позначається операція градієнт?
-
Запишіть визначення операції градієнт у векторному аналізі через оператор
 .
. -
Запишіть формулою у тензорному представленні операцію градієнт від скаляра
 .
. -
Як змінює ранг тензорного поля операція градієнт?
-
Скільки операцій типу «градієнт» можна побудувати для тензорного поля r- го рангу?
-
Дайте визначення операції дивергенція тензорного поля.
-
Як позначається операція дивергенція?
-
Запишіть визначення операції дивергенція у векторному аналізі через оператор
 .
. -
Запишіть формулою у тензорному представленні операцію дивергенція від вектора
 .
. -
Як змінює ранг тензорного поля операція дивергенція?
-
Скільки операцій типу «дивергенція» можна побудувати для тензорного поля r- го рангу?
-
Дайте визначення операції ротор тензорного поля.
-
Як позначається операція ротор?
-
Запишіть визначення операції ротор у векторному аналізі через оператор
 .
. -
Запишіть формулою у тензорному представленні операцію ротор від вектора
 .
. -
Як змінює ранг тензорного поля операція ротор?
-
Скільки операцій типу «ротор» можна побудувати для тензорного поля r- го рангу?
-
Дайте визначення операції лапласіан тензорного поля.
-
Як позначається операція лапласіан тензорного поля?
-
Послідовному виконанню яких диференціальних операцій першого порядку еквівалентний лапласіан?
-
Лапласіан скалярного поля
 -
це: а) grad div
-
це: а) grad div
 ;
б) div grad
;
б) div grad
 ;
в) div
rot
;
в) div
rot
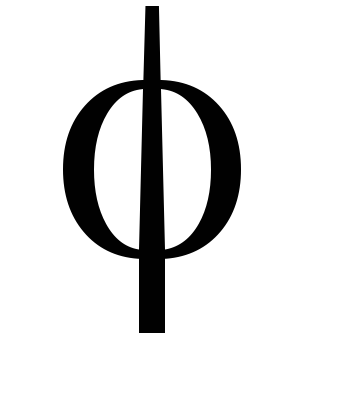 ;
г) rot
grad
;
г) rot
grad
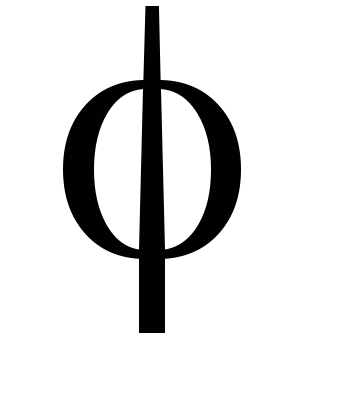 .
. -
Запишіть формулою у тензорному представленні операцію лапласіан від скаляра
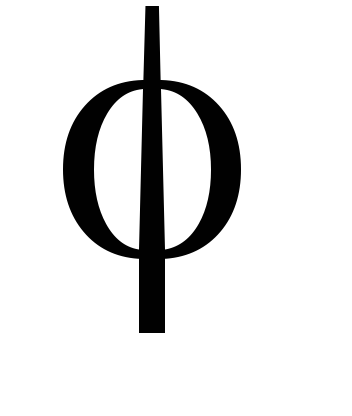 .
. -
Як змінює ранг тензорного поля операція лапласіан?
-
Скільки операцій типу «лапласіан» можна побудувати для тензорного поля r- го рангу?
-
Нехай
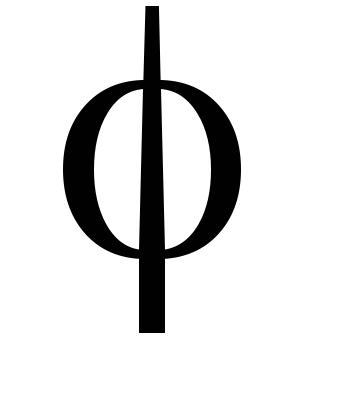 -
довільне скалярне поле, а
-
довільне скалярне поле, а
 -
довільне векторне поле. Тоді які з
наступних операцій можна виконати, а
які ні: а) grad div
-
довільне векторне поле. Тоді які з
наступних операцій можна виконати, а
які ні: а) grad div
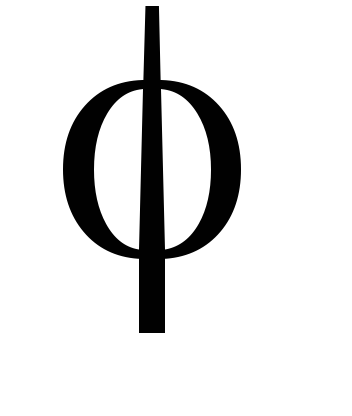 ;
б) grad div
;
б) grad div
 ;
в) grad
rot
;
в) grad
rot
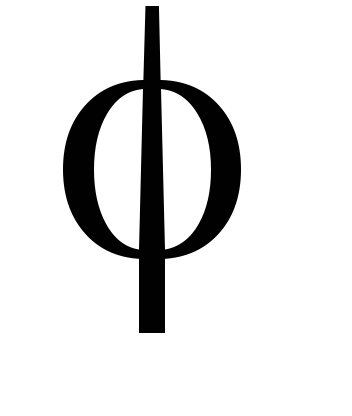 ;
г) grad
rot
;
г) grad
rot ?
? -
Нехай
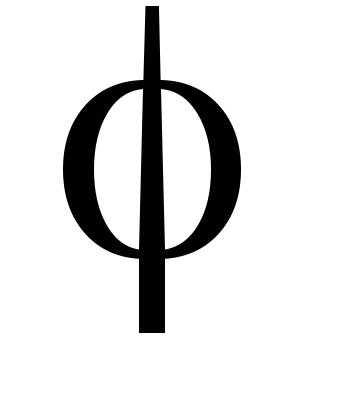 -
довільне скалярне поле, а
-
довільне скалярне поле, а
 -
довільне векторне поле. Тоді які з
наступних операцій можна виконати, а
які ні: а) div
grad
-
довільне векторне поле. Тоді які з
наступних операцій можна виконати, а
які ні: а) div
grad
 ;
б) div
grad
;
б) div
grad
 ;
в) div
rot
;
в) div
rot
 ;
г) div
rot
;
г) div
rot
 ?
? -
Нехай
 -
довільне скалярне поле, а
-
довільне скалярне поле, а
 -
довільне векторне поле. Тоді які з
наступних операцій можна виконати, а
які ні: а) rot
grad
-
довільне векторне поле. Тоді які з
наступних операцій можна виконати, а
які ні: а) rot
grad
 ;
б) rot
grad
;
б) rot
grad
 ;
в) rot
div
;
в) rot
div
 ;
г) rot
div
;
г) rot
div
 ?
? -
Нехай
 -
довільне скалярне поле, а
-
довільне скалярне поле, а
 -
довільне векторне поле. Тоді які з
наступних операцій можна виконати, а
які ні: а) grad
grad
-
довільне векторне поле. Тоді які з
наступних операцій можна виконати, а
які ні: а) grad
grad
 ;
б) grad
grad
;
б) grad
grad
 ;
в) div
div
;
в) div
div ;
г) div
div
;
г) div
div ?
? -
Нехай
 -
довільне скалярне поле, а
-
довільне скалярне поле, а
 -
довільне векторне поле. Тоді які з
наступних операцій можна виконати, а
які ні: а) rot
rot
-
довільне векторне поле. Тоді які з
наступних операцій можна виконати, а
які ні: а) rot
rot
 ;
б) rot
rot
;
б) rot
rot
 ;
в) grad
;
в) grad
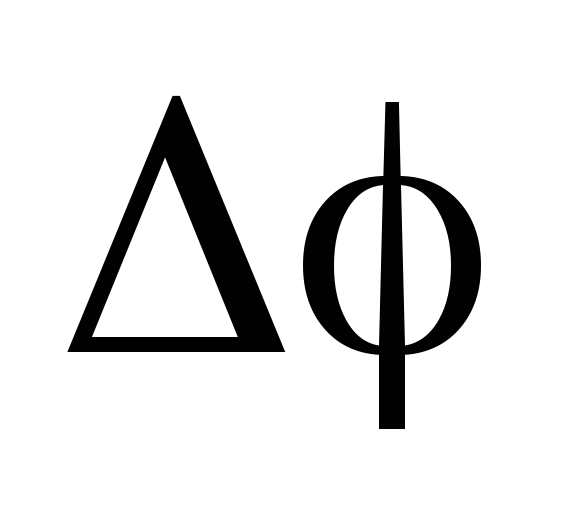 ;
г) div
;
г) div
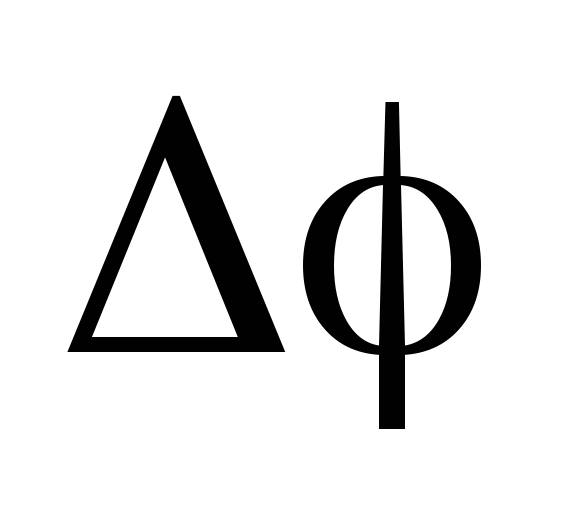 ?
? -
Нехай
 -
довільне векторне поле. Тоді чому
дорівнює div
rot
-
довільне векторне поле. Тоді чому
дорівнює div
rot
 ?
? -
Нехай
 -
довільне векторне поле. Тоді чому
дорівнює rot
rot
-
довільне векторне поле. Тоді чому
дорівнює rot
rot
 ?
? -
Що називається потоком векторного поля
 через поверхню S?
через поверхню S? -
Потік векторного поля
 через поверхню S задається формулою:
а)
через поверхню S задається формулою:
а)
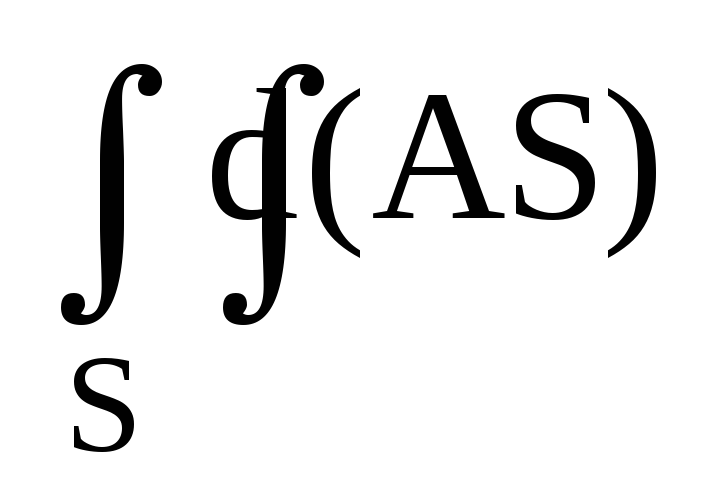 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 .
. -
Як направлений вектор
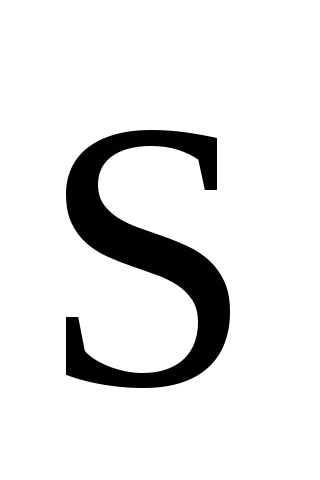 у формулі для потоку векторного поля
у формулі для потоку векторного поля
 :
:
 ?
? -
Запишіть формулою визначення потоку тензорного поля
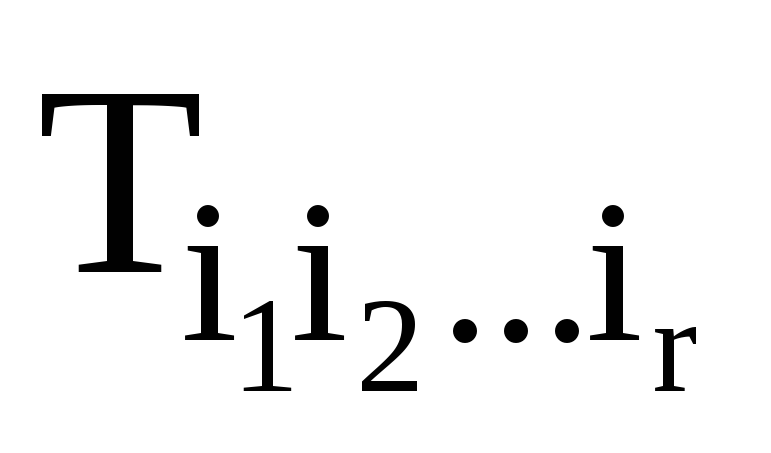 через поверхню S.
через поверхню S. -
Якщо ранг тензорного поля
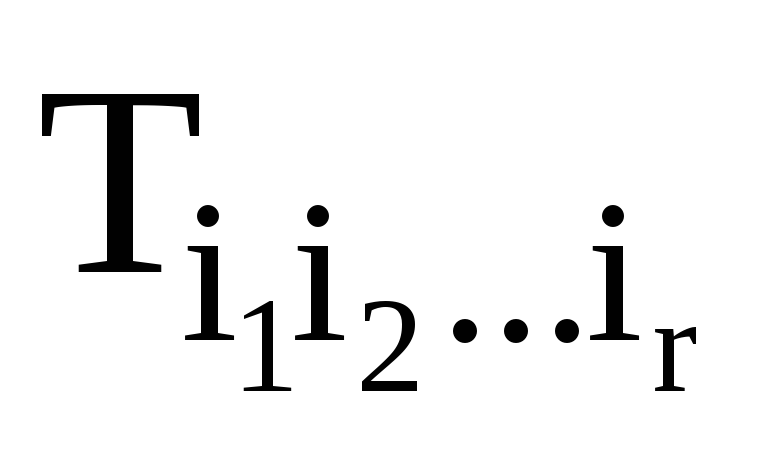 дорівнює r, то чому дорівнює ранг потоку
цього тензорного поля через поверхню
S?
дорівнює r, то чому дорівнює ранг потоку
цього тензорного поля через поверхню
S? -
Скільки різних потоків тензорного поля
 через поверхню S можна обчислити?
через поверхню S можна обчислити? -
Запишіть формулу Остроградського- Гауса з векторного аналізу.
-
Формула Остроградського- Гауса у векторному аналізі виглядає: а)
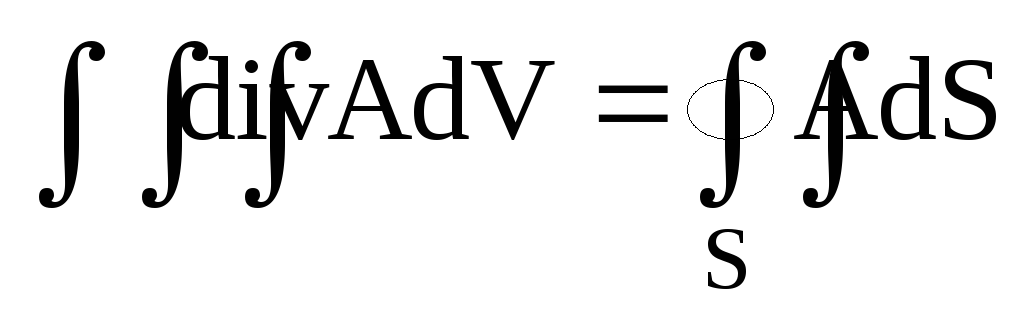 ;
б)
;
б)
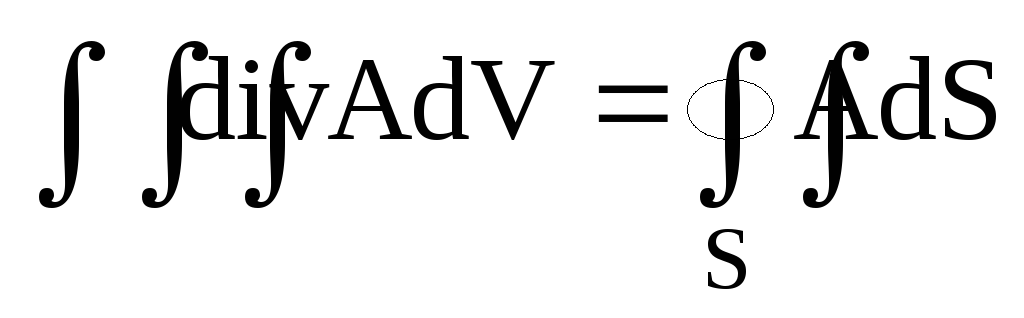 ;
в)
;
в)
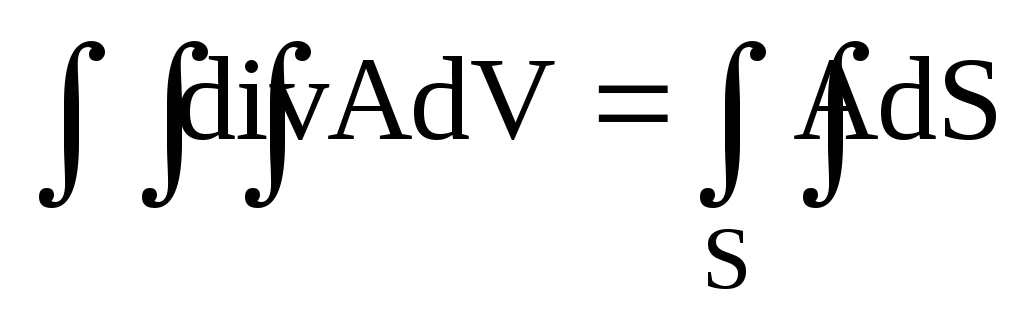 ;
г)
;
г)
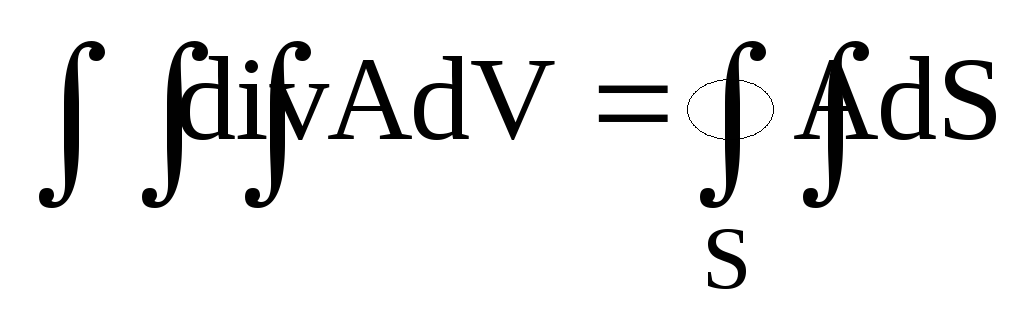 .
. -
Як направлений вектор
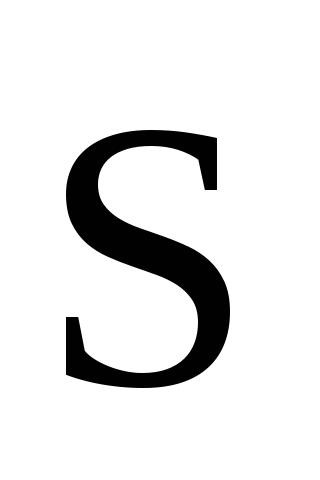 у формулі Остроградського- Гауса:
у формулі Остроградського- Гауса:
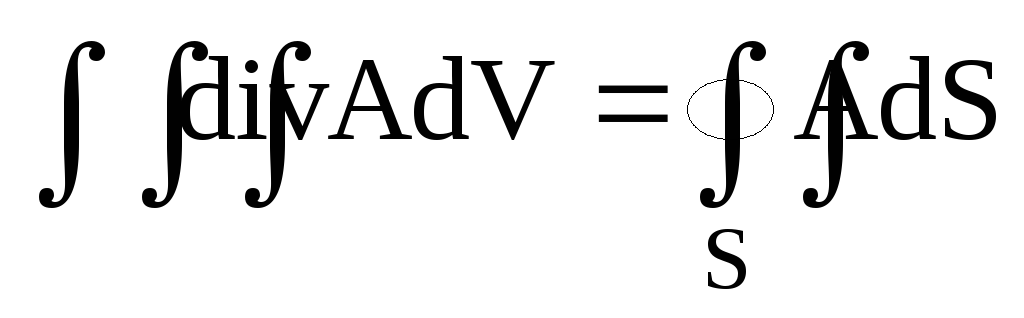 ?
? -
Запишіть формулу Остроградського- Гауса для тензорного поля
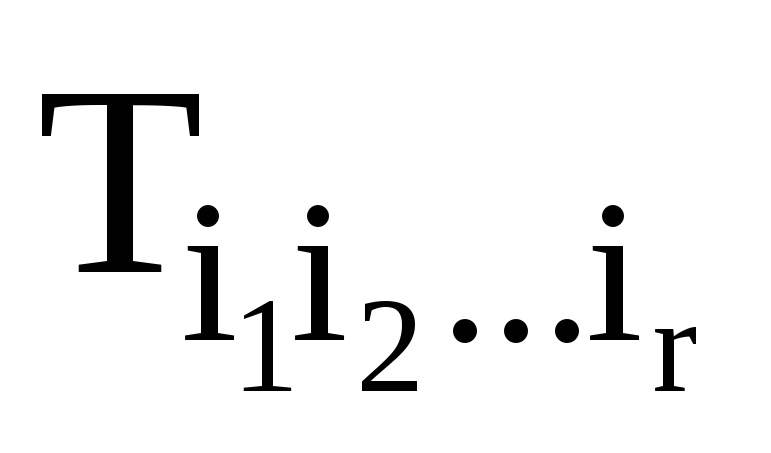 .
. -
Якщо ранг тензорного поля
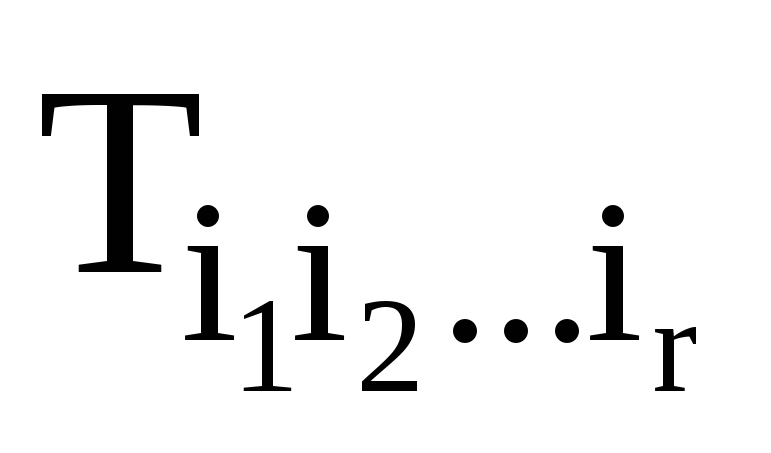 дорівнює r, то чому дорівнює ранг
тензорного поля з формули Остроградського-
Гауса?
дорівнює r, то чому дорівнює ранг
тензорного поля з формули Остроградського-
Гауса? -
Скільки різних формул типу «Остроградського- Гауса» можна побудувати для тензорного поля
 ?
? -
Запишіть формулу Стокса з векторного аналізу.
-
Формула Стокса у векторному аналізі виглядає: а)
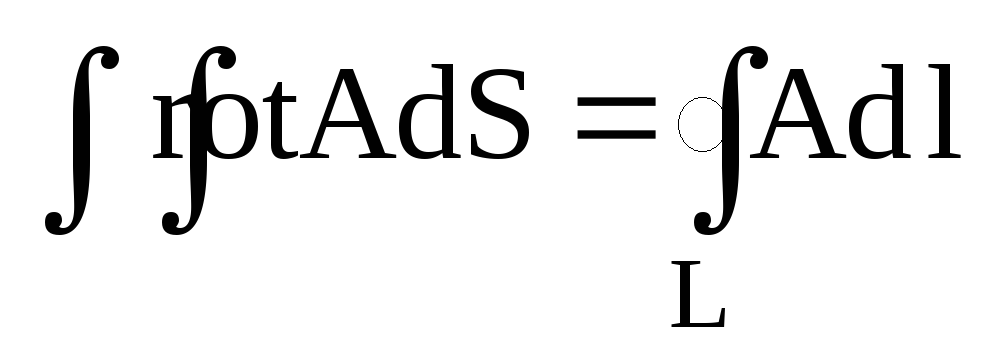 ;
б)
;
б)
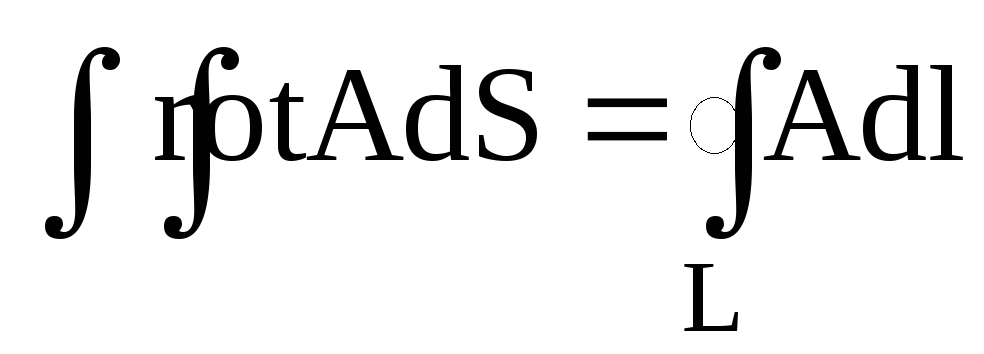 ;
в)
;
в)
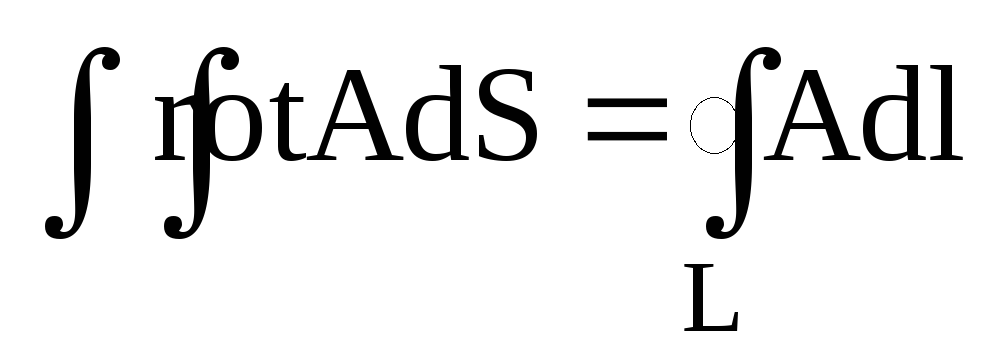 ;
г)
;
г)
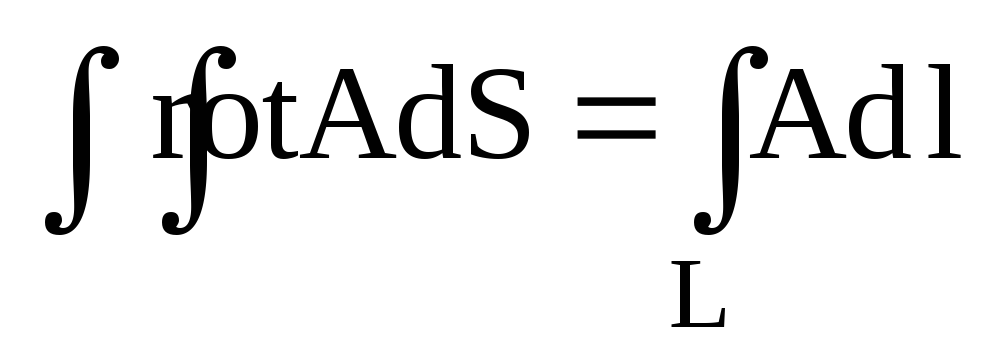 .
. -
Як направлений вектор
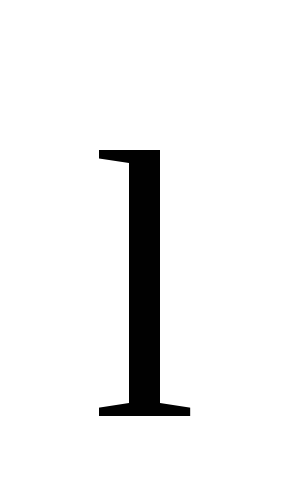 у формулі Стокса:
у формулі Стокса:
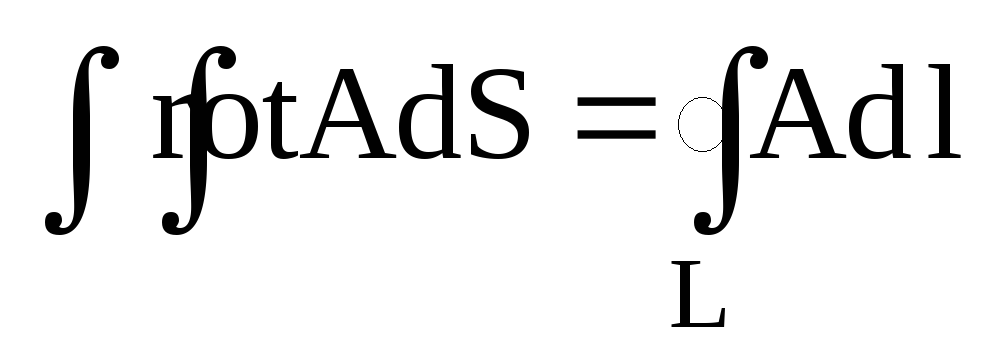 ?
? -
Запишіть формулу Стокса для тензорного поля
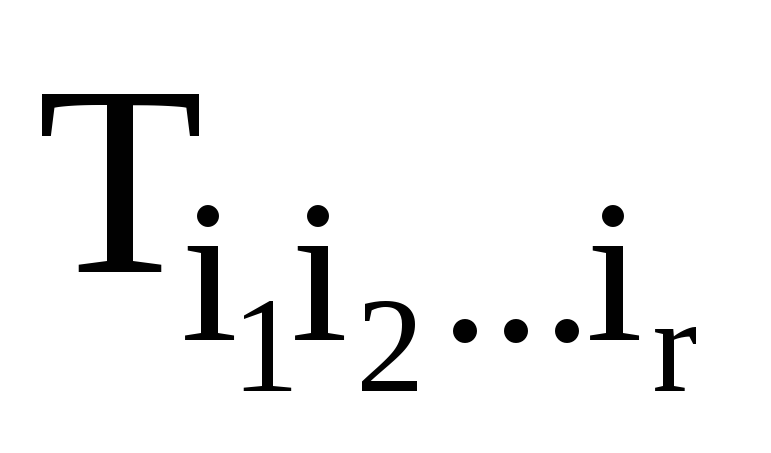 .
. -
Якщо ранг тензорного поля
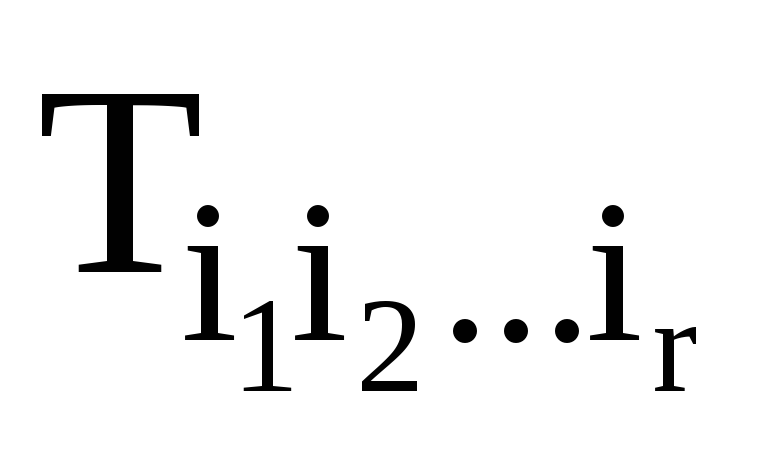 дорівнює r, то чому дорівнює ранг
тензорного поля з формули Стокса?
дорівнює r, то чому дорівнює ранг
тензорного поля з формули Стокса? -
Скільки різних формул типу «Стокса» можна побудувати для тензорного поля
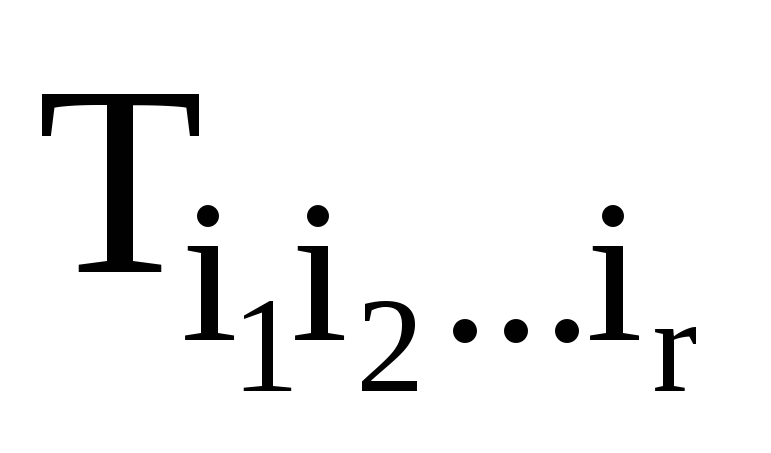 ?
? -
Якщо
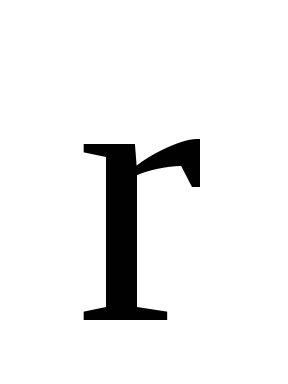 -
радіус- вектор
тривимірного простору,
то чому дорівнює
-
радіус- вектор
тривимірного простору,
то чому дорівнює
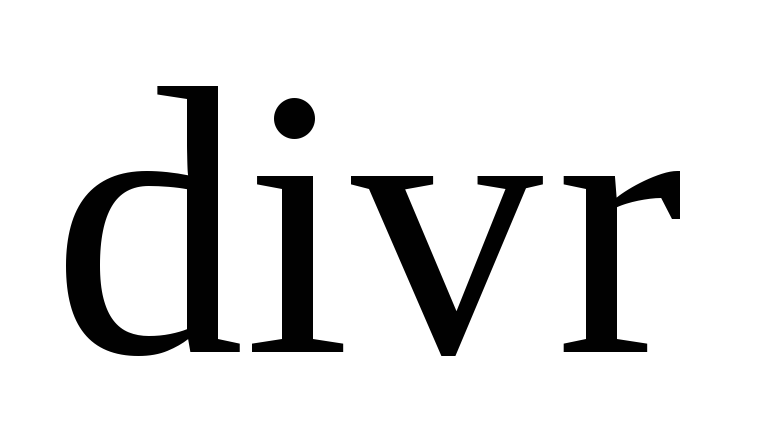 .
. -
Якщо
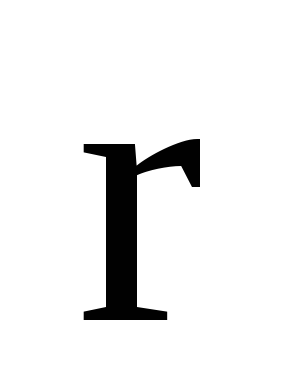 -
радіус- вектор тривимірного
простору,
то чому дорівнює
-
радіус- вектор тривимірного
простору,
то чому дорівнює
 .
. -
Якщо
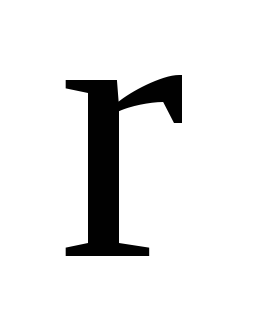 -
модуль радіус- вектора тривимірного
простору,
то чому дорівнює grad
r.
-
модуль радіус- вектора тривимірного
простору,
то чому дорівнює grad
r. -
Якщо
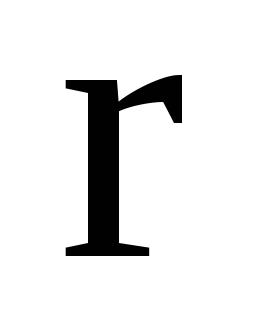 -
модуль радіус- вектора тривимірного
простору,
то чому дорівнює
-
модуль радіус- вектора тривимірного
простору,
то чому дорівнює
 .
. -
Якщо
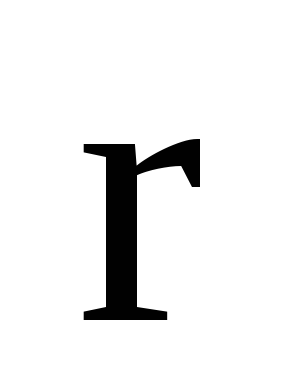 -
радіус- вектор
тривимірного простору,
-
радіус- вектор
тривимірного простору,
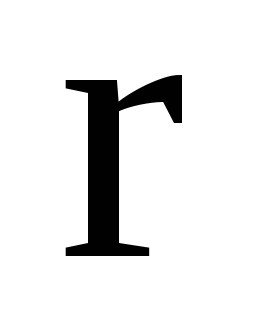 -
його модуль, то чому дорівнює
-
його модуль, то чому дорівнює
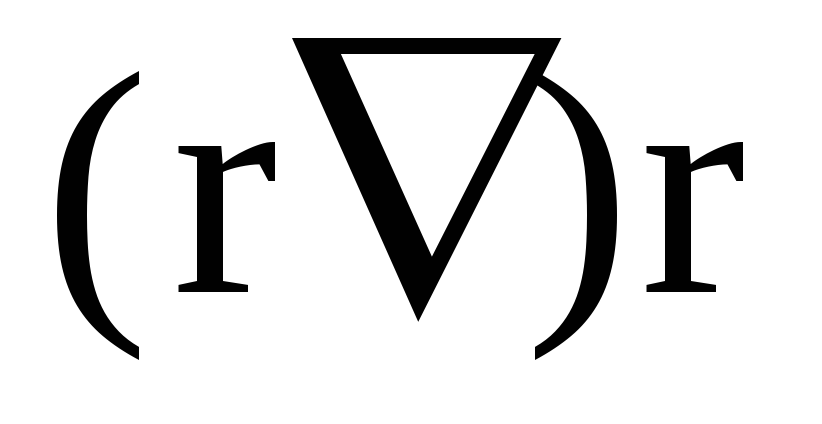 ?
? -
Якщо
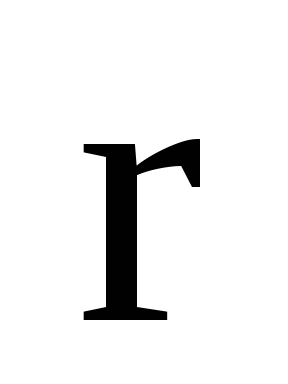 -
радіус- вектор
тривимірного простору,
-
радіус- вектор
тривимірного простору,
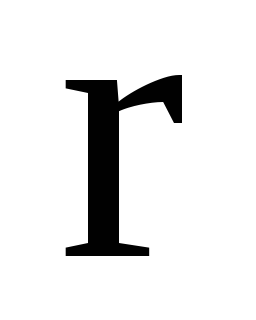 -
його модуль, то чому дорівнює
-
його модуль, то чому дорівнює
 ?
? -
Якщо
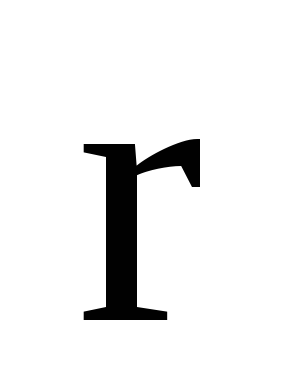 -
радіус- вектор
тривимірного простору,
-
радіус- вектор
тривимірного простору,
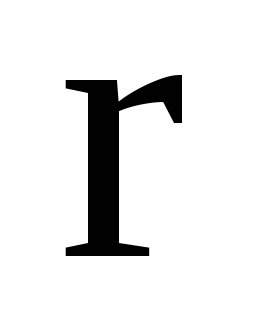 -
його модуль, то чому дорівнює
-
його модуль, то чому дорівнює
 ?
? -
Якщо
 -
радіус- вектор
тривимірного простору,
-
радіус- вектор
тривимірного простору,
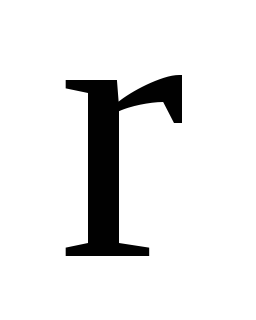 -
його модуль, то чому дорівнює
-
його модуль, то чому дорівнює
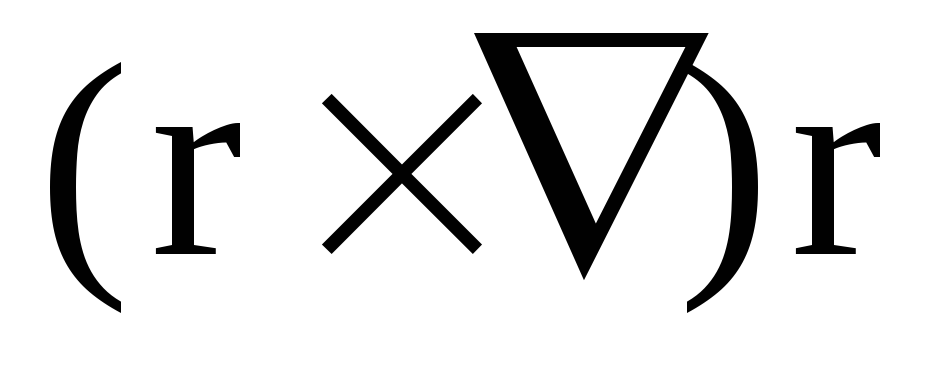 ?
? -
Якщо
 -
радіус- вектор
тривимірного простору,
-
радіус- вектор
тривимірного простору,
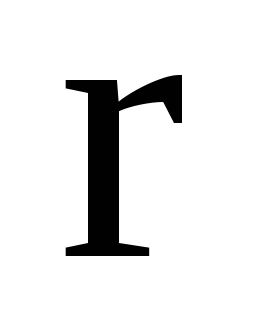 -
його модуль, то чому дорівнює
-
його модуль, то чому дорівнює
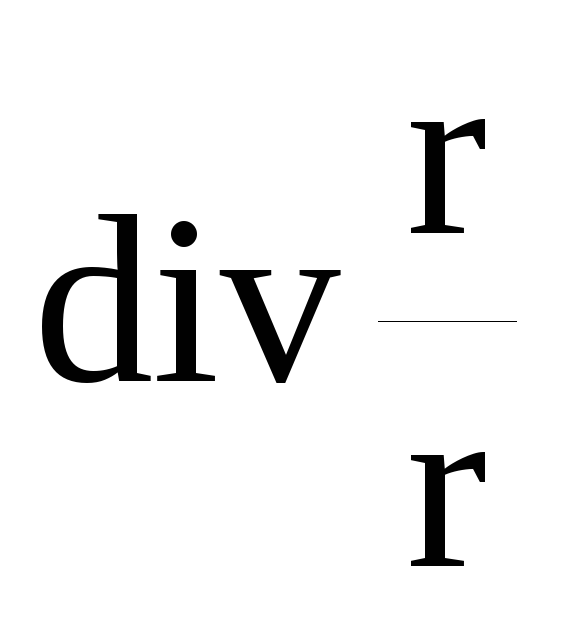 ?
? -
Якщо
 -
радіус- вектор
тривимірного простору,
-
радіус- вектор
тривимірного простору,
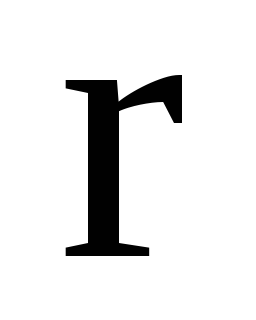 -
його модуль, то чому дорівнює
-
його модуль, то чому дорівнює
 ?
? -
Розпишіть за правилами тензорного аналізу подвійний векторний добуток векторів.
-
Дайте визначення групи.
-
Що означає фраза «коректно задати внутрішню операцію на елементах групи»?
-
Запишіть властивість асоціативності елементів групи.
-
Запишіть властивість «існування одиничного елемента» для елементів групи.
-
Запишіть властивість «існування оберненого елемента» для елементів групи.
-
Яка група називається абелевою?
-
Дайте визначення підгрупи.
-
Дайте визначення тривіальних підгруп.
-
Які групи називаються адитивними?
-
Наведіть три приклади адитивних груп.
-
Чи є множина раціональних чисел групою за операцією додавання?
-
Чи є множина цілих чисел групою за операцією додавання?
-
Чи є множина ірраціональних чисел групою за операцією додавання?
-
Які групи називаються мультиплікативними?
-
Наведіть три приклади мультиплікативних груп.
-
Чи є множина раціональних чисел групою за операцією множення?
-
Чи є множина цілих чисел групою за операцією множення?
-
Чи є множина додатних чисел групою за операцією множення?
-
Дайте визначення групи симетрій ромба.
-
Скільки елементів містить група симетрій ромба?
-
Чи є група симетрій ромба абелевою?
-
Дайте визначення таблиці Келі.
-
Як з таблиці Келі визначити чи є група абелевою?
-
Дайте визначення групи самосуміщень правильного трикутника.
-
Скільки елементів містить група самосуміщень правильного трикутника?
-
Чи є група самосуміщень правильного трикутника абелевою?
-
Дайте визначення перестановки.
-
Дайте визначення закону композиції перестановок.
-
Дайте визначення симетричної групи.
-
Як позначається симетрична група?
-
Скільки елементів містить група перестановок з 3 елементів?
-
Скільки підгруп по одному елементу містить група перестановок з 3 елементів?
-
Скільки підгруп по два елементи містить група перестановок з 3 елементів?
-
Скільки підгруп по три елементи містить група перестановок з 3 елементів?
-
Скільки всього підгруп містить група перестановок з 3 елементів?
-
Дайте визначення групи лишків за модулем два (группа вычетов по модулю два).
-
Скільки елементів містить група лишків за модулем два (группа вычетов по модулю два).
-
Дайте визначення групи ортогональних перетворень одновимірного евклідового простору.
-
Скільки елементів містить група ортогональних перетворень одновимірного евклідового простору?
-
Дайте визначення циклічної групи.
-
Як позначається циклічна група?
-
Наведіть приклад циклічної групи.
-
Дайте визначення групи коренів 8- го степеня з одиниці.
-
Що таке порядок циклічної групи?
-
Що таке утворюючий елемент циклічної групи?
-
Доведіть, що для елементів групи
 .
. -
Доведіть, що для елементів групи
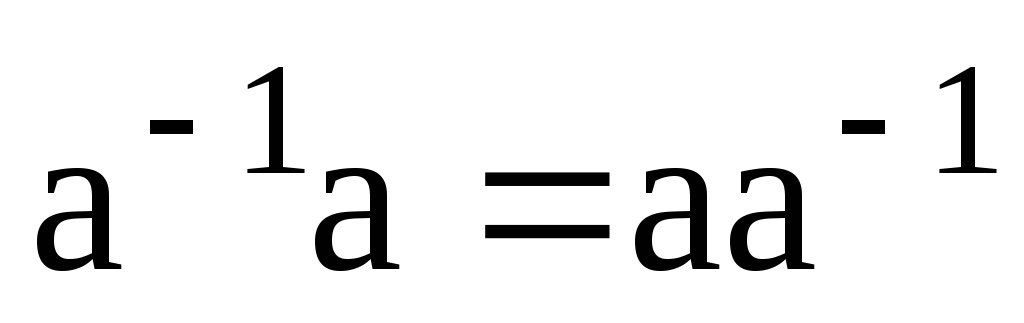 .
. -
Доведіть, що для елементів групи
 .
. -
Доведіть, що для елементів групи, якщо
 та
та
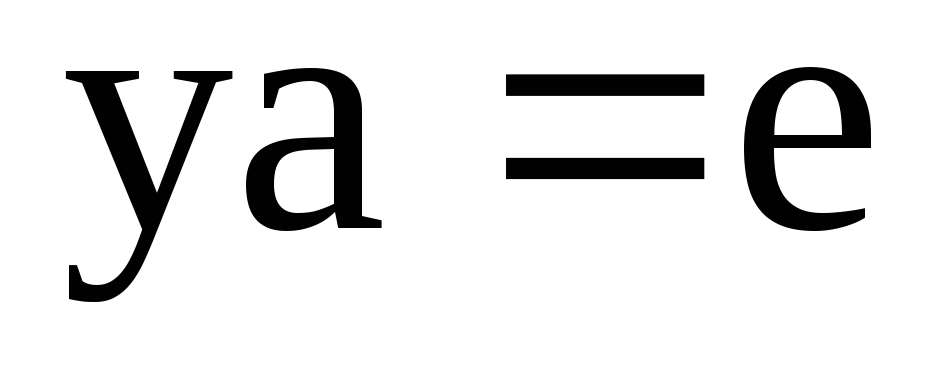 ,
то
,
то
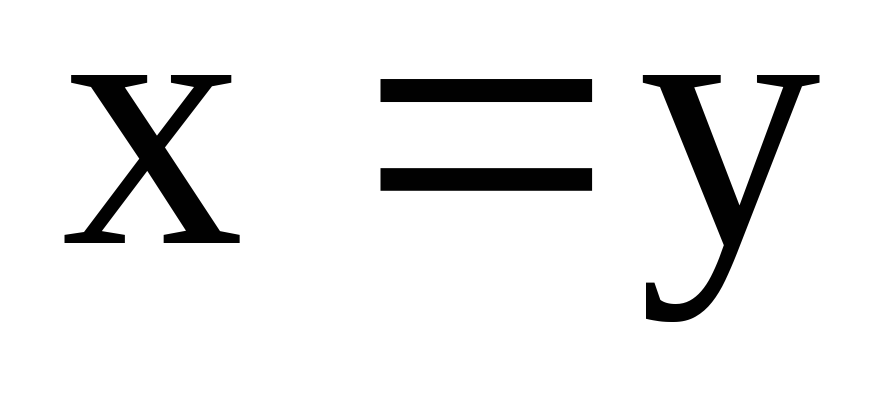 .
. -
Доведіть, що для елементів групи
 .
. -
Дайте визначення ізоморфізму двох груп.
-
Наведіть приклад двох груп, які є ізоморфними.
-
Дайте визначення автоморфізму.
-
Дайте визначення добутку двох підмножин довільної групи.
-
У якому випадку добуток двох підгруп також обов’язково є підгрупою?
-
Дайте визначення лівого суміжного класу підгрупи.
-
Дайте визначення правого суміжного класу підгрупи.
-
На основі властивостей суміжних класів, якщо
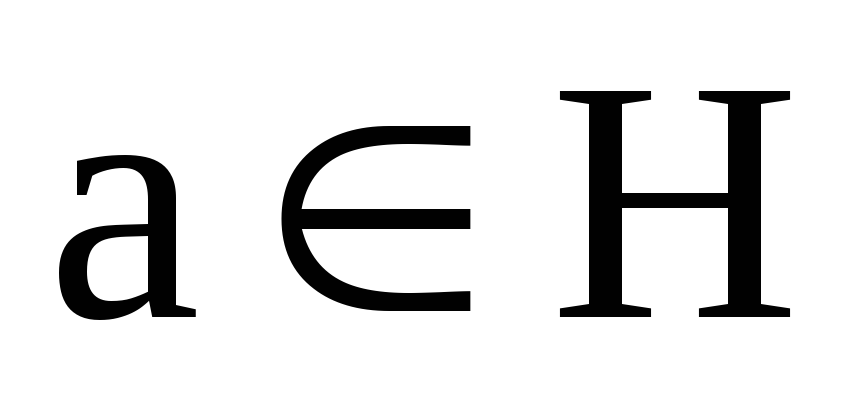 ,
то а)
,
то а)
 ;
б)
;
б)
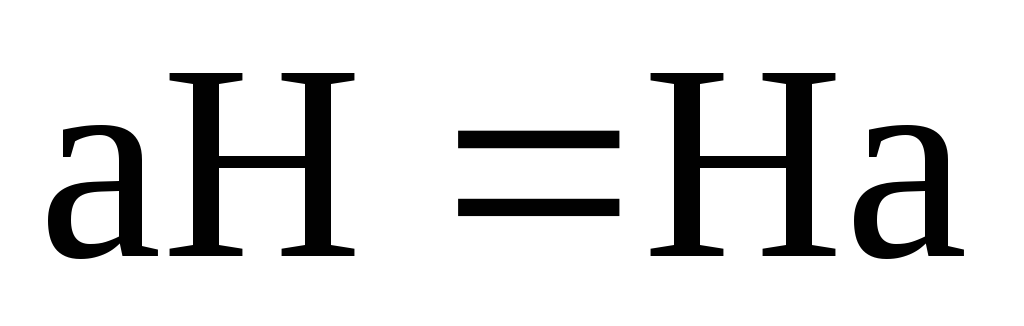 ;
в)
;
в)
 ;
г)
;
г)
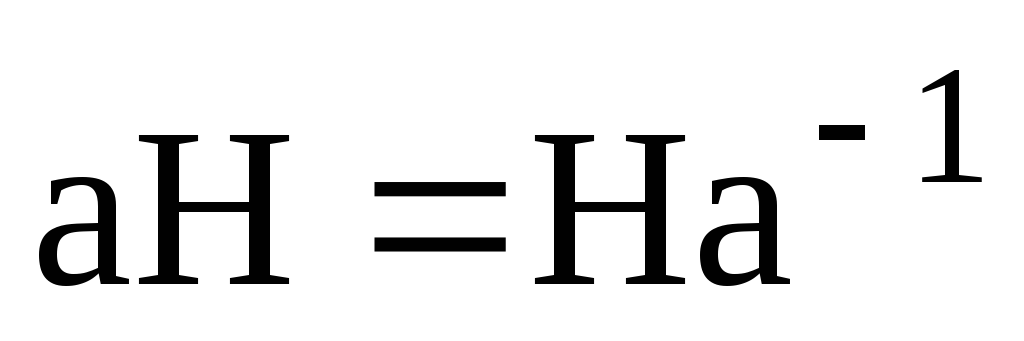 .
. -
На основі властивостей суміжних класів, якщо
 ,
то а)
,
то а)
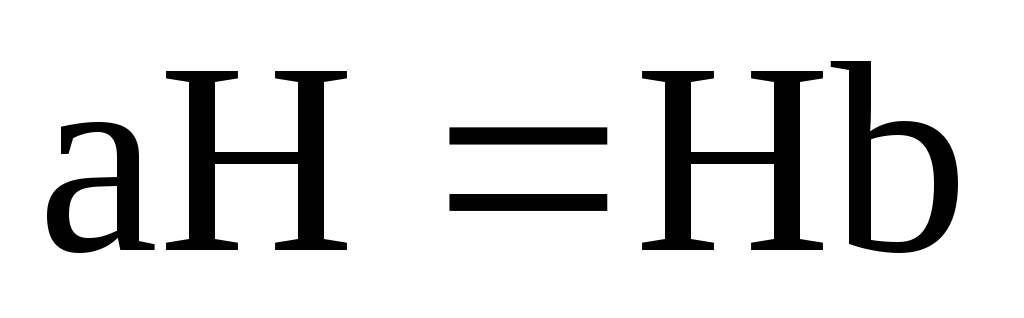 ;
б)
;
б)
 ;
в)
;
в)
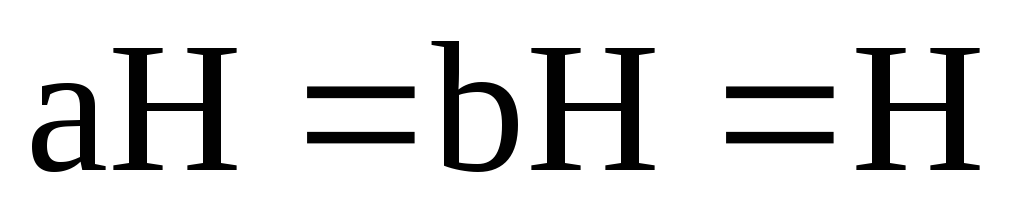 ;
г)
;
г)
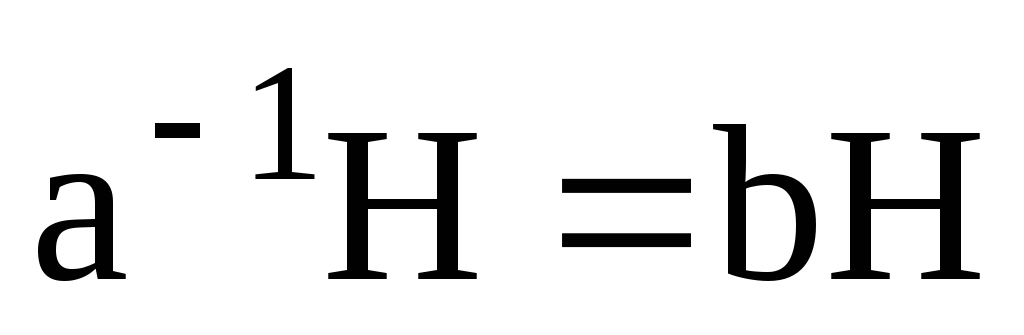 .
. -
На основі властивостей суміжних класів, якщо
 та
та
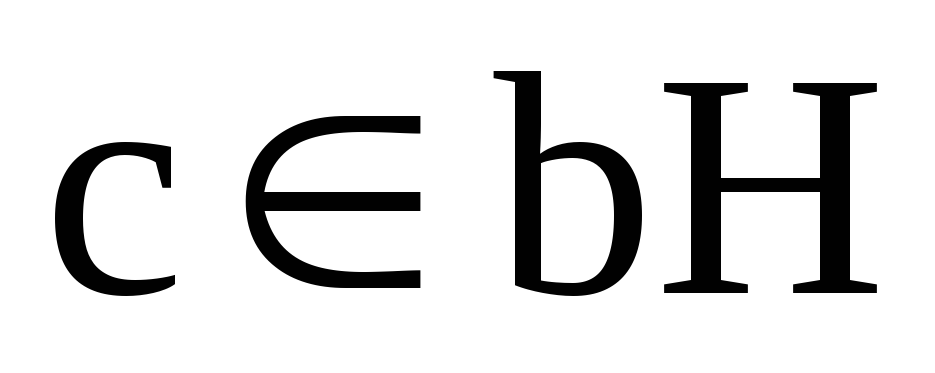 ,
то а)
,
то а)
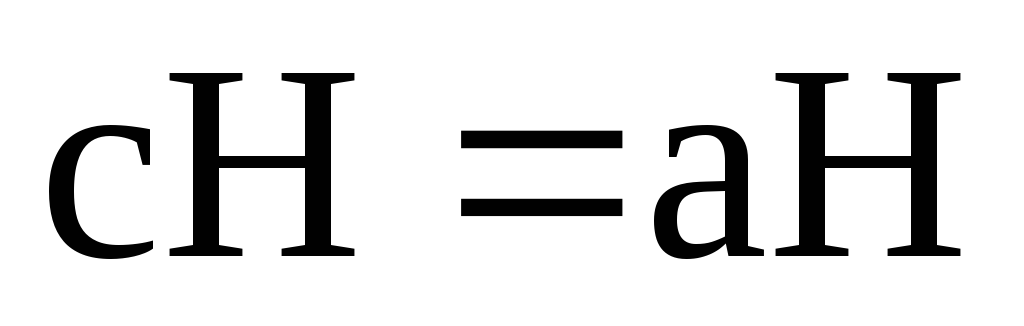 ;
б)
;
б)
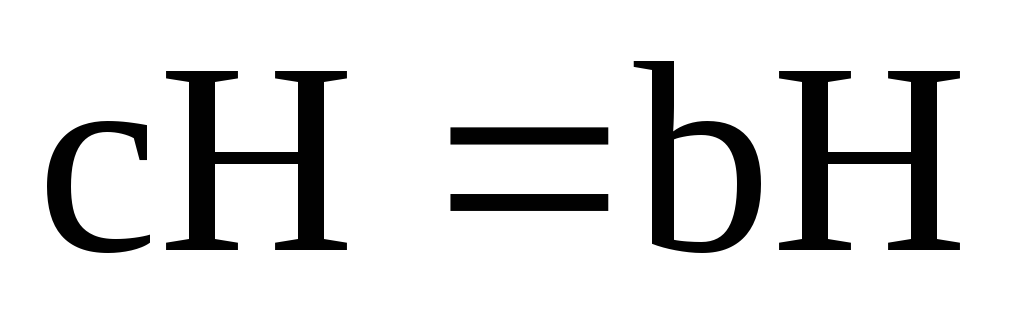 ;
в)
;
в)
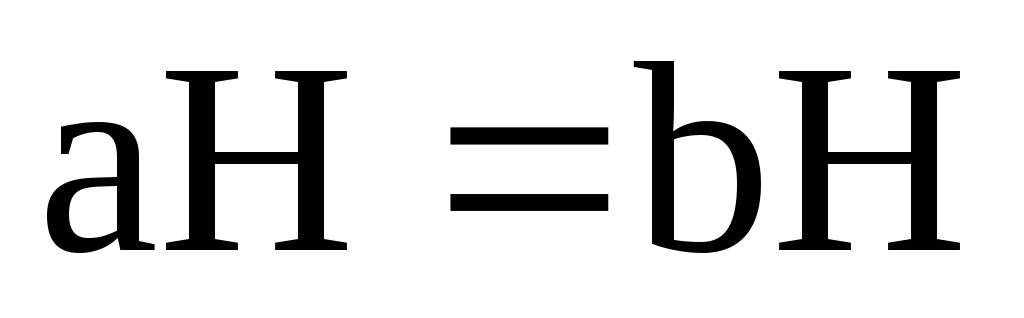 ;
г)
;
г)
 .
. -
На основі властивостей суміжних класів, у якому випадку
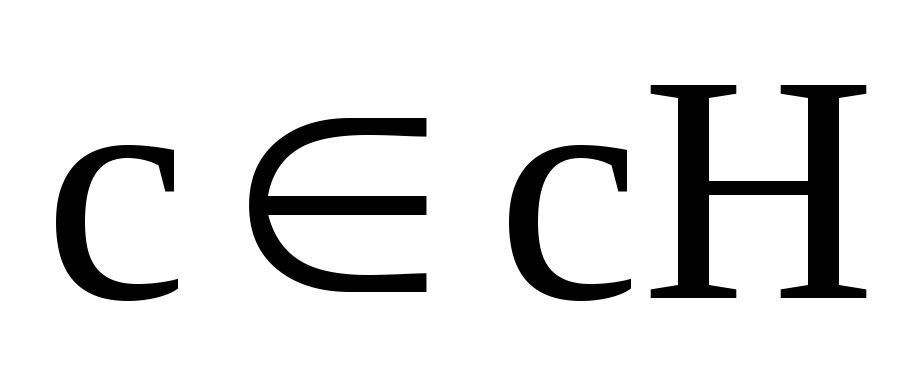 ?
? -
Дайте визначення нормального дільника групи.
-
Доведіть, що для нормального дільника групи добуток двох суміжних класів також є суміжним класом.
-
Дайте визначення гомоморфізму групи.
-
Дайте визначення гомоморфного образу групи.
-
Дайте визначення ендоморфізму групи.
-
Чим принципово відрізняється ізоморфізм групи від гомоморфізму групи?
-
За якої умови гомоморфний образ групи також є групою?
-
Дайте визначення фактор- групи групи G за нормальним дільником Н.
-
Як позначається фактор- група групи G за нормальним дільником Н?
-
Що є елементами фактор- групи групи G за нормальним дільником Н?
-
Дайте визначення групи невироджених лінійних перетворень n- вимірного лінійного простору.
-
Як позначається група невироджених лінійних перетворень n- вимірного лінійного простору?
-
Дайте визначення ортогональної групи в n- вимірному евклідовому просторі.
-
Як позначається ортогональна група з n- вимірного евклідового простору?
-
Дайте визначення вланої ортогональної групи в n- вимірному евклідовому просторі.
-
Як позначається власна ортогональна група з n- вимірного евклідового простору?
-
На прикладі трьох груп (група невироджених лінійних перетворень, ортогональна група, власна ортогональна група) покажіть які з них є підгрупами інших.
-
Дайте визначення мирового простору.
-
Дайте визначення мирової точки.
-
Дайте визначення мирової лінії.
-
Запишіть формулою, яку відстань проходить світловий сигнал в інерційній системі відліку, якщо його було запущено в момент часу t1 з точки (x1,y1,z1) та детектовано в момент часу t2 у точці (x2,y2,z2).
-
Дайте визначення інтервалу між двома подіями у мировому просторі.
-
Як позначається інтервал між двома подіями у мировому просторі?
-
Що означає для інтервалу принцип незмінності швидкості світла у різних системах відліку.
-
Які перетворення систем відліку називаються перетвореннями Галілея.
-
Які перетворення систем відліку називаються перетвореннями Лоренца.
-
Запишіть формулу як вводиться величина
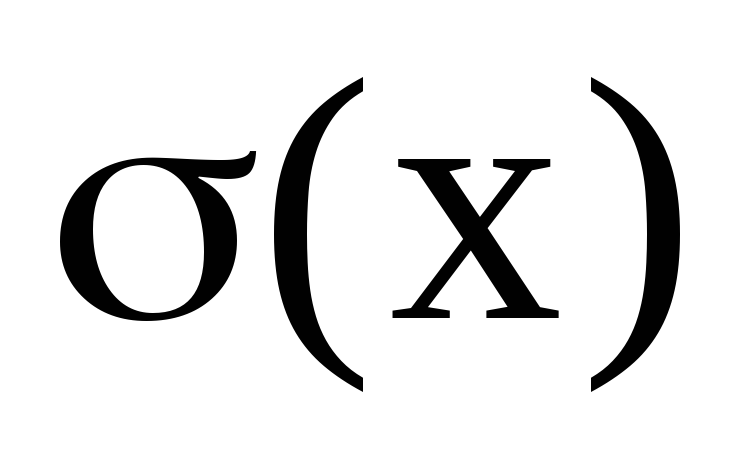 для інтервалу
для інтервалу
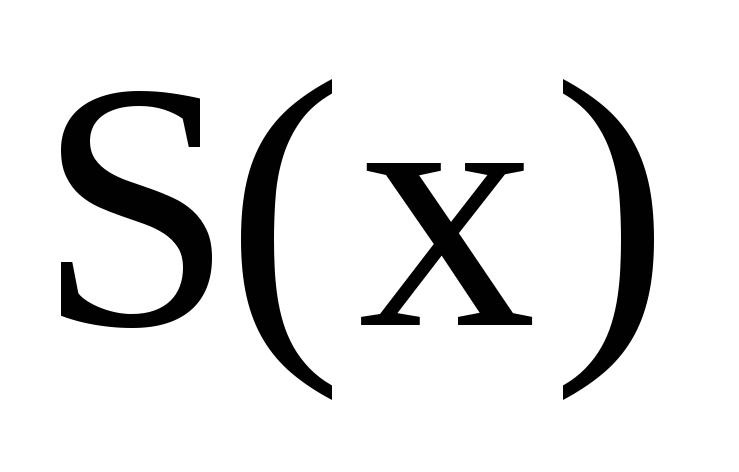 .
. -
Величина
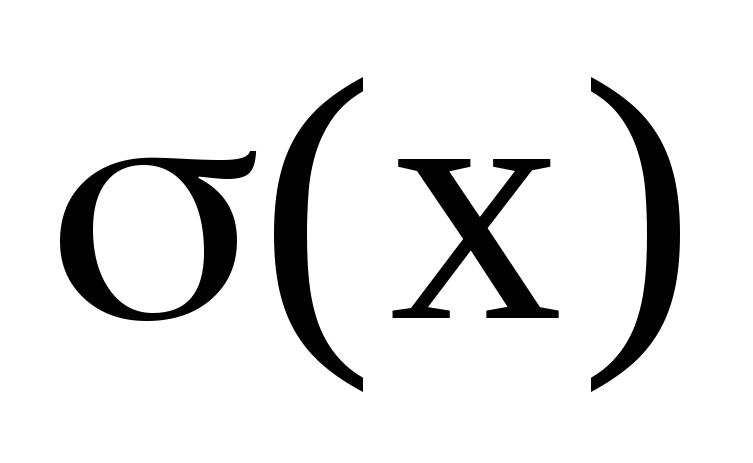 для інтервалу
для інтервалу
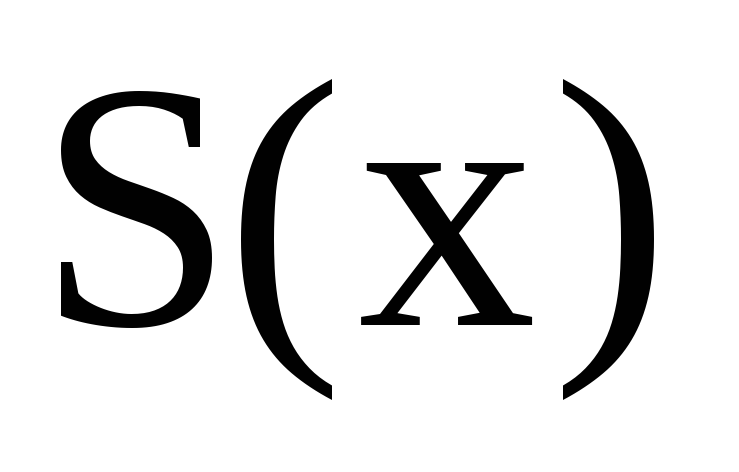 вводиться за наступною формулою: а)
вводиться за наступною формулою: а)
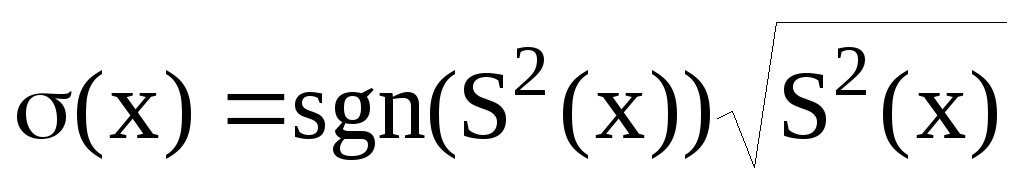 ;
б)
;
б)
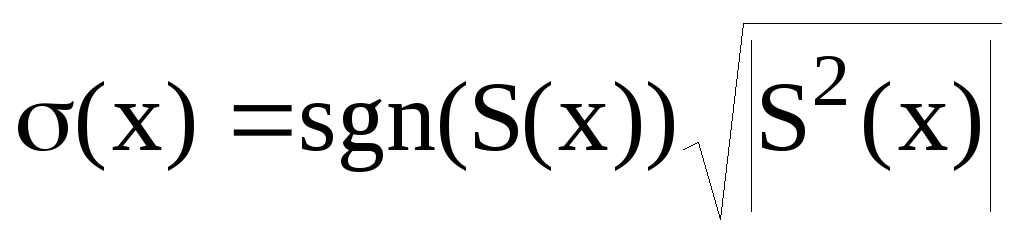 ;
в)
;
в)
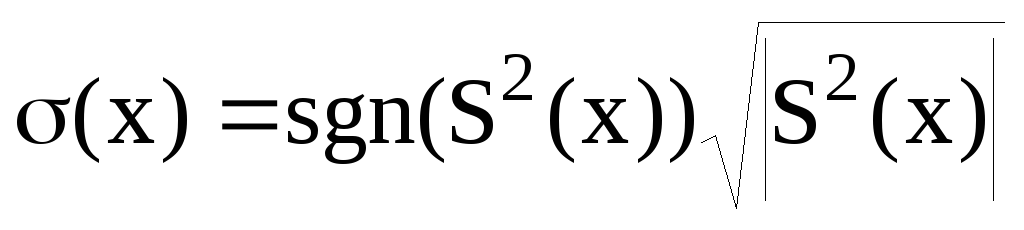 ;
г)
;
г)
 .
. -
Дайте визначення часоподібних векторів.
-
Дайте визначення ізотропних векторів.
-
Дайте визначення просторовоподібних векторів.
-
Якщо інтервал між двома подіями часоподібний, то як ці події можна пов’язати у деякій системі відліку К?
-
Якщо інтервал між двома подіями просторовоподібний, то як ці події можна пов’язати у деякій системі відліку К?
-
Дві події можна пов’язати причинно наслідковим ланцюгом, якщо інтервал між цими подіями який?
-
Дайте визначення псевдоевклідового простору
 .
. -
Запишіть формулою квадратичну форму, через яку (через полярну до неї білінійну форму) задається скалярний добуток у псевдоевклідовому просторі?
-
У чому принципова різниця між евклідовим та псевдоевклідовим просторами?
-
Дайте визначення перетворення Лоренца псевдоевклідового простору.
-
Що є аналогом перетворення Лоренца у евклідовому просторі?
-
Дайте визначення загальної групи Лоренца.
-
Як позначається загальна група Лоренца.
-
Дайте визначення повної групи Лоренца.
-
Як позначається повна група Лоренца?
-
Дайте визначення власної групи Лоренца.
-
Як позначається власна група Лоренца?
-
Дайте визначення групи Лоренца.
-
Як позначається група Лоренца?
