at_fizika

Таблица спектров механических моментов и их проекций

Примеры решения задач

Пример 7.1. Найти собственные функции и собственные значения

следующих операторов:

а) F x , если (x) = (x+a), где а =const.

41

где - собственное значение оператора F . Решим это уравнение для операторов а) и б): а)

.

Это линейное дифференциальное уравнение первого порядка, которое будем решать методом разделения переменных:

d dx .

Интегрируя это уравнение, получим

ln ln C x ,

откуда

x C e x

- собственная волновая функция оператора

F x ,

const C находится из условия нормировки.

Чтобы найти , накладываем на найденную волновую функцию заданное условие непрерывности

(x) = (x + a),

Ce x Ce x a Ce x e a .

из этого уравнения получим, что

e a 1,

или по теореме Эйлера

cos a sin a 1

Из полученного уравнения следует:

cos a 1

sin a 0

42

Из решения системы уравнений найдем, что

a 2 n 2 n a

- собственное значение оператора, где n = 0, 1, 2…

F x .

б)

d 2 dx2

или

+ = 0

– линейное дифференциальное уравнение второго порядка. Составим характеристическое уравнение:

Z2 + k2 = 0, где k2 = .

Так как корни этого характеристического уравнения мнимые

z12 k , решение дифференциального уравнения можно записать в

виде:

x C1sinêx C2 cosêx C1sin x C2 cos x,

где С1 и С2 – const.

Для нахождения накладываем на полученную волновую функцию

x C1sin x C2 cos x ,

заданные граничные условия, а именно:

0 C2 0,

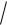C1sin 0 n ,

где n = 0, 1, 2……

Следовательно собственное значение оператора

d 2

F dx2 ,

будет иметь вид:

n 2 .

43

принадлежащее собственной волновой функции А(x) = exp (-x2/2).

Подействуем коммутаторами на произвольную волновую функцию

44

45

Задачи для самостоятельного решения

1 .Найти собственные значения и собственные нормированные функции

оператора L2z .

46

Практическое занятие № 8

Тема: Атом водорода по Шредингеру. Термы многоэлектронных атомов. Спин – орбитальное взаимодействие, тонкая структура атомных спектров.

Контрольные вопросы:

1.Что называют термом атома, его обозначение в виде символа, принятого в спектроскопии.

2.Квантовые числа, характеризующие квантовомеханическое состояние атома водорода в I-ом электростатическом приближении. Что они определяют, что характеризуют?

3.На основе какого принципа можно объяснить наличие электронных оболочек в атоме?

4.Какие квантовые числа имеет внешний, или валентный, электрон в основном состоянии атома калия?

5.От каких квантовых чисел зависит энергия терма атома с учетом спин – орбитального взаимодействия?

6.Чему равна спин – орбитальная мультиплетность, как она влияет на спектральные линии атомных спектров?

электростатическом приближении (без учета спин – орбитального взаимодействия).

n = 1, 2, 3,…(неограниченно) – главное квантовое число; Е0 = 13.6 эВ; m – масса электрона; M – масса ядра.

Буквенные обозначения орбитального квантового числа .

1s r,t R1s r e Et - волновая функция основного состояния атома водорода.

47

Учитывая, что энергия возбуждения атома водорода равна:

Е = Еn – Е1 , где Е1 = -13.6 эВ,

найдем энергию возбужденного состояния n:

Еn = -13.6 + 12.09 = -1.51 эВ.

Так как энергия возбужденного состояния n в атоме водорода

Пример 8.2. Найти средний электростатический потенциал, создаваемый 1s – электроном в центре атома водорода.

Решение

1s основное состояние атома водорода, которое описывается следующими квантовыми числами:

n = 1, 0, m 0 , ms 12 .

Среднее значение потенциала найдем по квантовомеханическому рецепту:

здесь dV = 4 r2dr (сферическая симметрия).

49

Взяв интеграл, найдем, что

1s aeÁ .

Следовательно, электростатический потенциал, создаваемый 1s – электроном в центре атома водорода определяется величиной заряда

электрона e и наиболее вероятным расстоянием 1s – электрона от ядра аБ.

Пример 8.3. Выписать возможные типы термов атома, содержащего кроме заполненных оболочек два электрона, s и p.

Решение

Возможные типы термов атома с учетом спин – орбитального взаимодействия определяются возможными значениями полного квантового числа j.

Так как для замкнутых оболочек всегда L = 0 и S = 0, то полный орбитальный момент и полный спиновый моменты атома в целом будут определяться векторной суммой соответствующих моментов s и p – электронов.

50