выражение (3.10) для переданной энергии, то получим сечение передачи энергии

В общем случае соответствующие аналитические ряды для сечения рассеяния позволяют получать выражения, справедливые для больших значений z2 и

более высоких энергий путем учета более высоких степеней в разложении по

параметрам z2α и β .

Приведенные результаты не учитывают, строго говоря, взаимодействия налетающего электрона с электронами атома, а также радиационных поправок, обусловленных тормозным излучением электрона в поле ядра. По физическому смыслу эти механизмы приводят к неупругим потерям энергии. Как известно из классической электродинамики, интенсивность тормозного излучения пропорциональна квадрату ускорения электронов в поле ядра:

I (z2e2 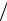me )2 . Это означает, что радиационные поправки могут стать

существенными для рассеяния назад и особенно для столкновений с ядрами, обладающими большим z2 . Формула для потерь энергии электрона на

тормозное излучение была получена в рамках квантовой электродинамики Бете и Гайтлером, о чем будет сказано в разделе, касающемся тормозной способности различных частиц. Заметим, наконец, что результаты, полученные для электронных столкновений, по существу применимы также и к столкновениям позитронов с атомами.

3.3 Столкновения тяжелых заряженных частиц с атомами

Как уже отмечалось, исследование статического, зависящего от расстояния взаимодействия между двумя атомами, представляет собой чрезвычайно трудную задачу многих тел, которую, строго говоря, следует решать методами квантовой теории. В динамической ситуации, подобной столкновению, это взаимодействие обычно зависит также от относительной скорости. Кроме того, необходимо принимать во внимание неупругие процессы – возбуждение электронов и ионизацию атомов. Во многих задачах, связанных с образованием радиационных повреждений (дефектов), относительная скорость невелика по сравнению со скоростями орбитальных электронов, а неупругие потери энергии, связанные с ионизацией и возбуждением, незначительны по сравнению с кинетической энергией налетающей частицы и атома-мишени. Поэтому во многих случаях ими можно пренебречь, в результате чего процесс рассеяния удается описать с помощью некоторого адиабатического потенциала межатомного взаимодействия V (r) ,

возможные типы которого обсуждались выше. Этот потенциал определяется

увеличением полной энергии системы из двух атомов, каждый из которых находится в основном состоянии, во время их медленного сближения из бесконечности до относительного расстояния r . Для сферическисимметричных атомов (ионов) потенциал можно считать, очевидно, центральным: V (r ) =V (r) .

Наоборот, при скорости частиц большей, чем скорость орбитальных электронов, по среде будет двигаться ядро с зарядом z1e, взаимодействие

которого с атомами мишени не является упругим. Что касается потенциалов межатомного взаимодействия, о которых говорилось ранее, то лишь для

передачи энергии σ(T; E1 ) можно представить в аналитической форме, которая вытекает непосредственно из общей формулы Резерфорда:

При расчете сечений во всех других случаях используют либо численные, либо приближенные аналитические методы. Например, одним из подходящих подгоночных потенциалов для экранированного кулоновского взаимодействия

является степенной потенциал V (r) = Crn . Для этого потенциала

где n >1 и Γ(x +1) = x!- гамма-функция. Расходимость полных сечений рассеяния

Tm

σ(E1 ) = ∫σ(T; E1 )dT

0

для всех неэкранированных потенциалов кулоновского взаимодействия, которые физически не являются слишком реалистичными при описании атомных систем, присуща и дифференциальным сечениям (3.14) и (3.15). Однако здесь ситуация такая же, как и для быстрых электронов – впоследствии для оценок физически важных величин понадобятся лишь парциальные сечения с конечным нижним пределом интегрирования или интегральные средние вида

для которых не возникает больших проблем даже в случае классического кулоновского взаимодействия. Если же в выражении (3.16) использовать общий степенной потенциал, то никаких проблем при T → 0 не возникает вовсе, как это следует из (3.15), если n >1.

Сечение образования атомов отдачи при описании межатомных

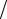
взаимодействий с помощью кулоновского потенциала дается выражением, которое получается аналогично парциальному сечению (3.7)

Макроскопическое сечение рассеяния для ионов получается умножением выражения (3.17) на n2 . Главной и весьма важной общей особенностью

сечений (3.7) и (3.17) является то, что они увеличиваются с уменьшением начальной энергии E1 по крайней мере до тех пор, пока соответствующая

величина максимальной передаваемой энергии Tm остается заметно больше значения пороговой энергии Td . Это означает, что при замедлении быстрых

заряженных частиц их способность создавать структурные дефекты в результате появления атомов отдачи возрастает вне зависимости от общих потерь энергии, связанных с другими процессами. Используя (3.7) или (3.17), несложно определить энергию частиц E1 , при которой сечение рассеяния с

возникновением атомов отдачи максимально. Дифференцируя (3.7) или (3.17) по E1 и приравнивая результат нулю, получаем следующее значение энергии

Последняя формула предсказывает совсем небольшое значение энергии E1 для иона, что выводит ее, строго говоря, за пределы применимости,

поскольку при малых энергиях взаимодействие имеет более сложный неупругий характер. Пиковое значение энергии для электронов существенно выше из-за очень небольшой величины соответствующего параметра α . Отметим также, что сечение (3.17) на несколько порядков больше, чем сечение (3.7), благодаря множителю m1 m2 ~1. Кроме того, величина Tm =αE1

в (3.17) соизмерима с энергией налетающего иона E1 , что также увеличивает

сечение процесса и вероятность прямого образования атомов отдачи для тяжелых частиц.

3.4 Кинетика неупругого столкновения тяжелой частицы с атомом

Рассмотрим теперь подробнее влияние неупругих процессов на кинетику рассеяния при взаимодействии атомов. Взаимодействие атомов можно считать упругим, как это вытекает из общего квантовомеханического рассмотрения, только при определенных условиях. При подходящих прицельных расстояниях столкновения между атомами могут быть неупругими, как показано в разделе 2, и при малой, и при большой начальной энергии частицы независимо от природы процессов неупругого рассеяния. В частности, кроме ядерных реакций некоторое количество Q кинетической

энергии может расходоваться на электронные переходы. В результате

начальная энергия E1 сталкивающихся частиц оказывается больше, чем их кинетическая энергия E1′ +T после столкновения, причем разность энергий равна неупругим потерям Q :

E1 = E1′ +T + Q .

Все неупругие процессы, связанные с электронными переходами, уже перечислялись – это возбуждение и ионизация атомов, а также обмен атомными электронами. По смыслу проблемы корректное вычисление величины Q и соответствующего сечения для какого-то конкретного из

вышеперечисленных процессов оказывается практически невозможным без грубых упрощающих предположений, поскольку для этого нужно решить задачу многих тел, которая дополнительно включает в себя возможность квантовых переходов.

В то же время возможно корректное описание кинетики процесса неупругого рассеяния, для чего не требуется никаких подробностей о характеристиках взаимодействия и электронных переходах. Для этого нужно лишь учесть неупругие потери энергии Q в системе центра инерции. Это

означает, что относительная энергия Eотн = µv2 2 = µv12 2 , имевшаяся до столкновения, уменьшается в процессе столкновения на величину Q , которая

зависит от прицельного расстояния, или, что то же самое, от угла рассеяния в системе центра инерции. Следовательно, относительную энергию после столкновения можно записать в виде разности

Eотн′ = Eотн −Q(ϑ).

С другой стороны, если относительную энергию выразить через относительную скорость при помощи равенства Eотн′ = µv′2 2 и подставить в

последнее равенство, то получается следующее выражение для относительной скорости после столкновения:

В соответствии с (3.19) относительная скорость уменьшается, поэтому векторная диаграмма для процесса неупругого рассеяния, показанная на рис.3.2, отличается от обычной тем, что импульс µv′ в относительной системе

отсчета для всех значений угла рассеяния ϑ меньше соответствующего значения импульса µv . В результате вектор p1′ конечного импульса

налетающей частицы описывает в пространстве импульсов не окружность, а некоторую замкнутую кривую, которая полностью лежит внутри окружности, соответствующей упругому рассеянию. Понятно, что каждому конкретному процессу неупругого столкновения отвечает своя функция Q(ϑ) и

определенная форма кривой. На рис.3.2 схематически показана связь между углами и импульсами только для случая равных масс, поскольку другие

Рис.3.2 Векторная диаграмма рассеяния при неупругом рассеянии частиц с равной массой m1 = m2

диаграммы получаются аналогично.

Как видно из рисунка, в общем случае новая кривая пересекается с окружностью только в одной точке, соответствующей рассеянию вперед, поскольку при таком рассеянии взаимодействия вообще нет и потери энергии равны нулю. Максимальны же неупругие потери энергии при рассеянии назад. В действительности векторные диаграммы представленного типа не вполне точны, если процесс неупругого взаимодействия приводит к ионизации, при которой в процессе столкновения выбивается один или несколько электронов. Выбитые вторичные электроны уносят не только энергию, но и импульс, что не отражено в приведенных выше рассуждениях. С другой стороны, из-за малой массы электронов их импульсы можно считать пренебрежимо малыми при всех разумных передачах энергии.

В соответствии с рис.3.2 в процессе упругого рассеяния все угловые характеристики в лабораторной системе отсчета – угол рассеяния ϑ1 и угол

отдачи ϑ2 , оказываются больше, чем при неупругом. В частности, непосредственно из рис.3.2 для угла рассеяния ϑ1 получаем

изменения углов рассеяния, причем неоднозначная зависимость угла рассеяния ϑ от угла ϑ1 может появиться не только при равных массах частиц,

но даже в том случае, когда налетает более легкая частица.

Из рис.3.2 можно получить также аналитические соотношения, связывающие долю неупругих потерь в начальной энергии сталкивающихся частиц. Например, соотношение, связывающее Q(ϑ) с начальной энергией E1

через кинематические характеристики частиц после столкновения, имеет вид:

словами, достаточно выделить после столкновения любую из сталкивающихся частиц, но измерить одновременно ее энергию и угол рассеяния. Отметим, что кинетика процесса неупругого рассеяния полностью определяется суммарными потерями энергии Q при столкновении и не зависит от доли

энергии, получаемой каждой из частиц, поскольку неупругие процессы, например, возбуждение атома, могут происходить в каждом атоме по отдельности или в обоих сразу.

Физические процессы при неупругом рассеянии весьма сложно описать количественно и поэтому необходимо больше экспериментальных данных, чем информация об углах рассеяния и энергиях. Экспериментальные данные свидетельствуют о том, что степень неупругости столкновения и неупругие потери энергии Q возрастают по мере того, как два атома все более

проникают друг в друга. Иными словами, небольшая величина расстояния максимального сближения и достаточно большой угол рассеяния ϑ способствуют, как схематически показано на рис.3.2, неупругим потерям энергии. О важности расстояния максимального сближения, как меры неупругости рассеяния, свидетельствует такой экспериментальный факт – степень неупругости процесса рассеяния лишь незначительно меняется при при одновременном увеличении, либо одновременном уменьшении энергии налетающей частицы E1 и прицельного расстояния b. Необходимо только,

чтобы не изменялось существенно значение rm .

Существуют и некоторые качественные соображения, которые делают более понятными сложные физические процессы при неупругом рассеянии и могут служить отправной точкой для их приемлемого описания. Большая масса ядер по сравнению с массой электронов позволяет, во-первых, рассматривать движение двух ядер отдельно от электронов и, во-вторых, описывать их траектории классическим способом. Это связано с малой дебройлевской длиной волны относительного движения ядер, которая меньше атомных размеров вплоть до тепловых энергий. В этом случае для описания процесса рассеяния используют известный метод прицельного расстояния, в рамках которого при классически движущихся ядрах только поведение электронов требует квантового описания. Тогда поведение атомных электронов при столкновении можно описать качественно как результат процессов, происходящих с электронными оболочками. А именно, по мере