При облучении биологических объектов кроме химически активных короткоживущих радикалов воды появляются также высокореактивные радикалы макромолекул. Радикалы макромолекул могут взаимодействовать между собой и с кислородом воздуха, поэтому у многих полимеров, как и в ДНК, вместо слабо связанных длинных полимерных молекул образуется жесткий трехмерный каркас. В результате полиэтилен, полихлорвинил и многие резины становятся жесткими и теряют пластичность, а фторированные полимеры при облучении в присутствии кислорода не просто теряют прочность и пластичность, а полностью превращаются в порошок. Наибольшей же устойчивостью к облучению обладают материалы на основе ароматических углеводородов.

7.2 Образование и устойчивость дефектов в кристаллах

Рассмотрим подробнее процесс образования точечных дефектов в кристаллах. Этот вопрос имеет самостоятельную ценность, если учесть возрастающее применение радиационных технологий и достижений радиационного материаловедения в медицине и медицинской промышленности. С другой стороны, такое рассмотрение наиболее простого и наглядного случая поможет, тем не менее, сделать некоторые общие выводы, справедливые для биологических объектов и полезные при построении радиобиологических моделей физического уровня.

Для образования точечного дефекта быстрая налетающая частица должна передать атому решетки или молекулы вполне определенное количество энергии. Первичный выбитый атом или атом отдачи оставляет после себя вакансию и размещается в окружающей решетке, искажая ее структуру. В самом простом случае при передаче энергии от частицы облучения атому решетки образуется только один дефект Френкеля. При достаточно большой энергии, переданной первичному выбитому атому, он может до своей полной остановки сместить из узлов другие атомы решетки, которые называют вторичными. Имея достаточный запас энергии, вторичные атомы также смещают решеточные атомы. Такой процесс называется каскадом смещений. Понятно, что ввиду особенностей механизма передачи энергии легкие частицы (электроны и позитроны) и γ -кванты могут

порождать каскады смещений только при очень больших энергиях.

Если передаваемая одному атому кинетическая энергия T меньше некоторого энергетического порога смещения или энергии смещения Td , то

вся переданная атому энергия в конечном счете превратится в тепло. Иными словами, энергия колебаний атома, оставшегося в своем узле (или молекуле), распространится по решетке (молекуле) и превратится в энергию тепловых колебаний. Если переданная энергия оказывается больше Td , то атом, покинув

узел и оставив вакансию, пройдет определенное расстояние и станет

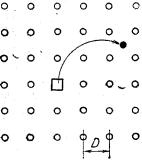
межузельным атомом, как показано на рис.7.2. Скорость, с которой начинает двигаться первичный атом из своего узла, всегда очень велика, поскольку в соответствии с экспериментальными данными порог Td составляет

величину порядка 14–35эВ. При этом в виде потенциальной энергии образованного дефекта запасается в действительности около Ed =5эВ (запасенная энергия),

так что основная часть переданной энергии порядка 20эВ – Рис.7.2 это кинетическая энергия смещенного атома. При такой самой минимальной из возможных кинетических энергий атом алюминия, например, имеющий массовое число A =27, будет двигаться

со скоростью v =1,2 106см/с. Следовательно, расстояние порядка постоянной решетки D ≈2Å он преодолеет за время около t =1,7·10-14с. Размер дефекта Френкеля, который образуется при пороговой энергии, составляет несколько

постоянных решетки, поэтому процесс образования дефекта завершается через

10-14–10-13с.

Частота тепловых колебаний, в которых участвуют все атомы решетки, не превышает 1013Гц, поэтому их в описанном процессе образования дефекта можно считать покоящимися. В то же время, именно в тепло уходит в конечном итоге большая часть переданной пороговой энергии. Новый межузельный атом существенно изменяет конфигурацию решетки в своей окрестности, поскольку решетка вынуждена “приспосабливаться” к новой неравновесной структуре. Аналогичные изменения происходят и в окрестности вакансии, причем вначале релаксация решетки заключается в рассеянии энергии возникающих колебаний в виде тепла. Устойчивость образованного дефекта Френкеля определяется величиной запасенной энергии, которая может высвобождаться, например, во время отжига при более высокой температуре благодаря диффузии дефектов. Запасенная потенциальная энергия представляет собой внутреннюю энергию поля внутренних напряжений. Этот избыток энергии может вызвать притяжение между вакансией и межузельным атомом и стать причиной исчезновения дефекта даже в отсутствие их диффузии. Иными словами, поле внутренних напряжений, порожденных дефектом Френкеля, может привести к его исчезновению в результате так называемой атермической или спонтанной рекомбинации. В результате полное время всех процессов релаксации, включая спонтанную рекомбинацию, значительно превышает время самого процесса смещения.

С учетом описанного процесса спонтанной рекомбинации можно говорить о некоторой неоднозначности определения величины порога смещения Td . То определение, которое использовалось до сих пор для

описания образования дефекта, показывает, сможет ли атом участвовать в процессе каскада смещений безотносительно к тому, что произойдет в

дальнейшем с образовавшейся парой вакансия – межузельный атом. Можно, однако, ввести порог смещения как такую минимальную сообщенную энергию, при которой происходит необратимое смещение атома с учетом тех возмущений и полей напряжений, которые он вызывает в решетке. Экспериментально эту энергию измерить существенно легче, поскольку она непосредственно определяется числом оставшихся в решетке дефектов.

Вероятность процесса рекомбинации уменьшается, а вероятность необратимости смещения увеличивается, очевидно, с ростом расстояния между вакансией и межузельным атомом. Под объемом неустойчивости или рекомбинационным объемом V0 дефекта Френкеля понимают все возможные

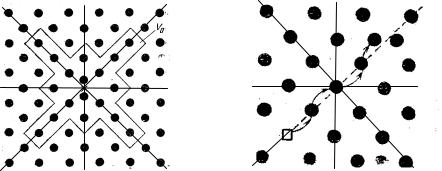
положения соответствующей вакансии вокруг межузельного атома, для которых появившийся дефект Френкеля будет неустойчивым. Кроме того, расстояние необратимого смещения зависит от взаимной ориентации оси дефекта Френкеля, проходящей через вакансию и межузельный атом (см. рис.7.1), и осей кристаллической решетки. По этой причине рекомбинационный объем всегда имеет существенно несферичную форму, как показано на рис.7.3. Для обеспечения устойчивости расстояние между вакансией и межузельным атомом должно быть порядка нескольких постоянных решетки, особенно вдоль направлений плотной упаковки, поэтому в металлах рекомбинационный объем содержит порядка 100 узлов решетки.

Интересно, что межузельный атом, который в итоге занимает устойчивое положение, не обязательно является тем самым атомом, который был непосредственно выбит налетающей частицей и оставил после себя вакансию. Выбитый атом может столкнуться с ближайшим соседом и занять его место, в то время как образовавшийся в результате такого столкновения замещения соседний атом принимает на себя роль первичного выбитого атома. Процесс продолжается до тех пор, пока каждый новый вовлеченный в него

а) б)

Рис.7.3. Рекомбинационный объем (а) и направления легкого смещения относительно центра пары межузельных атомов, который представляет собой центр рекомбинационного объема V0 для вакансии, и образование дефекта

Френкеля (б) в результате последовательности столкновений замещения вдоль одного из направлений легкого смещения.

атом имеет достаточную для смещения кинетическую энергию. Особенностью процесса последовательных столкновений замещения является то, что они происходят преимущественно вдоль плотноупакованных атомных рядов, как показано на рис.7.3б. В результате образуется дефект Френкеля с довольно большим расстоянием вдоль направления плотной упаковки, которое называется направлением легкого смещения. Вне зависимости от типа решетки

иравновесной конфигурации образующихся межузельных атомов и вакансий в дефекте Френкеля направлениям наиболее плотной упаковки соответствует минимум пороговой энергии и энергии первичной выбитой частицы в каскаде. Понятно, что устойчивость дефекта Френкеля не зависит от того, является ли межузельный атом первичным выбитым атомом или появился в процессе последовательных столкновений замещения.

Роль температуры в описанных выше процессах сводится к двум факторам. Во-первых, температура определяет амплитуду тепловых колебаний и характерную величину поля мгновенных перемещений атомов решетки относительно равновесных положений в тот момент времени, когда проходит быстрый процесс смещения. В результате локальное положение образованного межузельного атома при данной энергии отдачи и направлении движения оказывается равновесным, строго говоря, только относительно этой мгновенной квазистатической конфигурации атомов решетки. Во-вторых, тепловые флуктуации приводят к тому, что взаимодействие между вакансией

имежузельным атомом перестает быть статическим. В результате вакансия, расположенная по соседству с границей рекомбинационного объема для статической решетки, может оказаться неустойчивой при учете тепловых флуктуаций. Последнее обстоятельство эквивалентно, очевидно, увеличению объема неустойчивости, который растет вместе с температурой, и способствует, например, термическому отжигу.

Взаключение отметим, что в состоянии термодинамического равновесия даже в идеальном кристалле присутствует определенное

количество дефектов. Если число дефектов Nd значительно меньше, чем общее число узлов решетки N2 и число межузельных позиций N2′, то

равновесное число дефектов Френкеля в соответствии с известной формулой Больцмана равно

Nd ≈ (N2 N2′)12 exp(−Ed 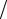2kT ).

Из этого выражения вытекает, что с повышением температуры равновесная концентрация дефектов Френкеля повышается. Однако при этом коэффициент диффузии также повышается с ростом температуры, поскольку зависит от нее, как правило, по закону

D ≈ D0 exp(−ED kT ),

где ED ~1эВ есть энергия активации процесса диффузии. Поэтому смысл процедуры отжига состоит в том, чтобы за счет интенсификации процессов

диффузии вернуть повышенную по каким-либо причинам концентрацию дефектов Френкеля к равновесному для температуры отжига значению. При энергии активации Ed ~1эВ и температуре T =1000°K это значение по порядку

величины равно Nd 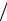(N2 N2′)12 ~10-12.

7.3 Пороговая энергия и сечение смещения

Понятно, что в любой структуре с выделенными, как в кристаллической решетке, направлениями пороговая энергия Td будет зависеть от направления

движения выбитого атома относительно выделенных. В решетках такие направления определяются кристаллографическими осями, о которых можно, например, говорить и применительно к макромолекулам в кристаллическом состоянии. В соответствии с этим вероятность смещения

является ступенчатой функцией направления движения с углами θ и ϕ в

произвольной, вообще говоря, системе координат относительно узла решетки. Анизотропная поверхность пороговой энергии, которая описывается функцией Td (θ,ϕ), зависит, как и рекомбинационный объем, от симметрии

кристалла и является обратной к поверхности объема неустойчивости в том смысле, что наименьшая величина пороговой энергии соответствует направлениям легкого смещения. Применение ступенчатой функции (7.1) является модельным, поскольку учет тепловых колебаний может размывать резкую границу функции вероятности смещения.

Зависящая от направлений функция пороговой энергии Td (θ,ϕ) является

основной величиной облучаемой решетки для процессов смещения, определяющей, в частности, интегральную (среднюю по направлениям) пороговую функцию или функцию смещений

которая в свою очередь описывает среднюю вероятность смещения атома из узла в произвольном направлении. Величина Pd (T ) является монотонно

возрастающей функцией переданной энергии, которая увеличивается от нуля до единицы в некотором интервале энергий Td ,min ≤T ≤Td ,max и равна единице

при T ≥Td ,max . В первом приближении сечение смещения первичного атома налетающей частицей с энергией E1 можно получить путем интегрирования произведения вероятности Pd (T ) смещения для атома, получившего энергию T , и дифференциального сечения σ(T; E1 ) передачи энергии T :