
- •1. ОСНОВНЫЕ ПОНЯТИЯ РАДИАЦИОННОЙ ФИЗИКИ
- •1.1 Ядерные излучения
- •Таблица 1.1
- •Уровни радиобиологических процессов
- •2.1 Пределы классического описания
- •2.4 Борновское приближение
- •2.6 Виды потенциалов взаимодействия
- •3.1 Столкновения электронов с атомами
- •3.2 Релятивистское и квантовое сечения рассеяния электронов
- •3.3 Столкновения тяжелых заряженных частиц с атомами
- •3.4 Кинетика неупругого столкновения тяжелой частицы с атомом
- •3.5 Рассеяние нейтронов на атомах
- •Задачи
- •4.1 Внешнее и внутреннее облучение
- •4.2 Виды пробегов частиц
- •4.3 Распределение векторных пробегов
- •4.4 Тормозная способность
- •4.5 Флуктуации потерь энергии частицы
- •Задачи
- •5.1 Торможение тяжелых ионов
- •5.2 Электронное торможение ионов
- •5.3 Ядерное торможение тяжелых ионов
- •Алюминий
- •Свинец
- •5.4 Пробег тяжелых ионов
- •Задачи
- •6.1 Рассеяние Мотта и потери энергии быстрых электронов
- •6.2 Разброс энергий и пробегов при многократном рассеянии электрона
- •6.4 Пробег и потери энергии нейтронов
- •Задачи
- •7.2 Образование и устойчивость дефектов в кристаллах
- •7.4 Каскадная функция
- •7.5 Пространственное распределение дефектов в каскаде
- •7.6 Полное число дефектов
- •8.1 Физические основы дозиметрии
- •7.2 Эквивалентная доза
- •7.4 Принципы попадания и мишени в радиобиологии
- •8.5 Другие физические модели
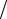
dNδ |
2πz2 n2 (z1e2 )2 |
1 |
1 |
|
|
|
||
dx = z2 n2σР (I;E1 ) = |
|
|
|
|
|
|
, |
(6.22) |
m v 2 |
|
− T |
||||||
I |
|
|||||||
|
e 1 |
|
|
|
m |
|
|
|
где I - средняя энергия возбуждения атома. Действительно, в соответствии с пояснениями к формуле (5.7) для коэффициента торможения B учет возбужденных состояний атома приводит к удвоению величины B . Поэтому классический коэффициент торможения, который фигурирует в формуле (4.24) и в полученном выражении (6.21), в первом приближении соответствует как раз той доле актов рассеяния, какую составляют среди процессов возбуждения и ионизации именно процессы ионизации атомов, приводящие к появлению δ -электронов.
Зависимость сечения образования δ -электронов (6.21) от заряда ионизующей частицы позволяет определить заряд методом подсчета числа δ - электронов на единице пути частицы в веществе. Наоборот, знание свойств первичного излучения позволяет с помощью формулы (6.21) оценить в первом приближении флюенс δ -электронов, разлетающихся от трека частицы. В соответствии с формулой (1.28) это дает в свою очередь информацию о вкладе δ -электронов в разнообразные реакции, индуцированные облучением. Выражение же для максимальной переданной энергии
T = |
4me m2 |
|
E ≈ |
4me E , |
||
|
|
|||||
m |
(m + m |
)2 |
1 |
m |
1 |
|
|
|
2 |
||||
|
e |
2 |
|
|
|
|
дает грубую оценку для энергии ионизующей частицы по пробегу δ - электрона и углу его вылета. Например, наличие вдоль протонного следа
следов δ -электронов с энергией T |
указывает на то, что энергия протона |
E1 ≈ Tm m2 4me ≥ 500T . С другой |
стороны, знание энергетических |
характеристик налетающих частиц позволяет сделать выводы о способности или неспособности δ -электронов участвовать в той или иной реакции, например, в прямом создании структурных дефектов, радикалов и т.д.
6.4Пробег и потери энергии нейтронов
Вконденсированных средах нейтроны способны вызывать появление структурных дефектов при прямой передаче энергии атомам, если их энергия превышает величину порядка 100эВ. Такие энергии характерны, например, для нейтронов с энергией в несколько МэВ, которые получаются в ядерных реакторах. Особый интерес с точки зрения образования радиационных повреждений представляют быстрые ( E1 ≥1МэВ), медленные ( E1 ≤500кэВ) и
тепловые нейтроны ( E1 ≈1/40 эВ). Характер взаимодействия таких нейтронов
с веществом мишени существенно различается и качественно определяется кинетической энергией нейтрона. Взаимодействие быстрых и медленных нейтронов с атомами большинства материалов мишени достаточно хорошо

описывается, как было показано, феноменологическим потенциалом жесткой сердцевины, который удовлетворительно отображает свойства упругого ядерного рассеяния и неупругого рассеяния в результате прямых ядерных реакций. В результате тормозная способность быстрых нейтронов определяется их энергией, в чем несложно убедиться, если в выражение (4.11) для тормозной способности подставить сечение рассеяния (3.28) жесткой сердцевины:
− |
dE |
= n2 |
Tm |
πR |
2 Tm |
n |
|
2 |
(6.23) |
1 |
∫Tσ(T; E1 )dT = n2 |
Tm |
∫TdT = |
|
2 |
πR Tm . |
|||
|
dRL |
|
0 |
0 |
2 |
|
|
||
Энергетические потери нейтрона проявляются в виде энергии отдачи, передаваемой атому мишени, и оказываются в большинстве случаев достаточно большими, чтобы образовать структурные дефекты посредством смещения атомов или разрыва молекулярных цепочек. С учетом равенства Tm =αE1 из выражения (6.23) вытекает линейная зависимость тормозной
способности быстрых нейтронов от энергии, поэтому с ростом энергии эффективность нейтронов с точки зрения образования структурных дефектов увеличивается. Это обстоятельство сильно отличает нейтроны от тяжелых заряженных частиц.
Используя выражения (4.13) и (6.23), несложно вычислить и полный линейный пробег нейтронов
|
E |
|
= (n2πR2 )−1 (1+ A) |
2 |
E0 |
|
|
|
RL (E0 ) = |
∫0 (−dE1 |
dRL )−1 dE1 |
ln |
, |
(6.24) |
|||
|
||||||||
|
Emin |
|
2A |
|
Emin |
|
||
который зависит от начальной кинетической энергии нейтрона логарифмическим образом и увеличивается с ростом энергии достаточно медленно. Здесь A- массовое число мишени, а величина Emin представляет
собой такое значение энергии, при которой нейтрон еще можно считать нетепловым и, соответственно, ограничиваться учетом только его упругого взаимодействия с ядрами. Несложно показать, что непосредственно из выражения (6.23) вытекает и экспоненциальный закон ослабления нейтронного пучка с глубиной.
Заметим, что полное сечение рассеяния быстрых нейтронов σ =πR2 относительно невелико и составляет величину порядка 1-10 барн. Поэтому длина свободного пробега λ нейтрона в мишени с типической для конденсированных сред плотностью n2 =1023 см-3 равна
λ =1 n2σ ≈1÷10см |
(6.25) |
и не зависит от энергии нейтрона. Следовательно, даже в макроскопическом образце мишени как быстрый, так и медленный нейтрон может испытать, по существу, всего лишь несколько упругих столкновений до выхода наружу. Разница между ними согласно (6.23) только в величине передаваемой при

каждом столкновении с ядром энергии. Все другие обсуждавшиеся до этого налетающие частицы взаимодействуют с материалом мишени настолько интенсивно, что останавливаются внутри любой макроскопической мишени, если это не тонкая фольга. В этом смысле поведение нейтрона (быстрого и медленного) прямо противоположно поведению других частиц.
С точки зрения хирургических применений в медицине указанное обстоятельство свидетельствует о не очень высокой эффективности применения нейтронных пучков. Понятно, что те несколько столкновений, которые нейтрон с достаточно большой энергией может испытать в теле пациента, относительно равномерно (см. задачу 6.3) распределяются по глубине, повреждая на своем пути здоровые ткани в не меньшей мере, чем патологически измененные. С другой стороны, тяжелые заряженные ионы расходуют практически всю свою энергию при электронном торможении. Это означает, что нужно тщательно подбирать характеристики ионных пучков, ориентируясь на максимальную эффективность ядерных столкновений именно в области локализации злокачественных тканей. Иной способ – это использование ядерного рассеяния высокоэнергетичных вторичных электронов, создаваемых быстрыми ионами, однако в этом случае снова практически невозможно локализовать поражающее действие.
Медленные и тепловые нейтроны могут захватываться ядрами атомов мишени, поэтому взаимодействие таких нейтронов с атомами мишени является в значительной степени неупругим. Сечение захвата медленного или теплового нейтрона ядром во многих случаях подчиняется закону Ферми
(2.36)
σ |
|
v−1 |
1 |
|
, |
(6.26) |
r |
E |
|||||
|
|
|
1 |
|
|
что объясняет рост сечения захвата с уменьшением скорости и энергии нейтронов. Вместе с тем, из общей формулы Брейта-Вигнера для радиационного захвата в разных областях энергии падающих нейтронов следует, что зависимость (6.26) справедлива, строго говоря, только вдали от резонансных уровней возбуждения ядра мишени. Если же энергия нейтрона приближается к некоторому резонансному значению W0 , то полное сечение с
учетом его упругой части начинает стремительно возрастать по закону
|
σtot = |
π |
|
|
ΓΓn |
|
, |
|
|
k 2 |
|
(E |
−W )2 + (Γ 2) |
2 |
|||
|
|
|
|
1 |
0 |
|
|
|
где (E ) =4,4·10-10/ |
|
- де-бройлевская длина волны нейтрона, Γ - |
||||||
E (эВ) |
||||||||
1 |
1 |
|
|
|
|
|
|
n |
парциальная ширина резонансного уровня возбужденного ядра с учетом возможности его распада с испусканием нейтрона и Γ- полная ширина уровня с учетом всех возможных распадов возбужденного ядра (γ -излучение,
испускание нейтрона, протона и т.д.).
Физическая причина резкого роста сечения захвата заключается в том,

что при небольших энергиях нейтрона возможно образование некоторого составного возбужденного ядра, способного существовать в течение достаточно больших промежутков времени. При этом величина энергии нейтрона, необходимая для образования составного ядра, должна соответствовать энергии одного из энергетических уровней возбуждения такого ядра. При радиационном захвате наибольший вклад в полную ширину резонансного уровня ядра (и время его жизни) дает распад с испусканием одного или более γ -квантов, поэтому Γ ≈ Γγ . В результате при резонансном
захвате, когда E1 =W0 , сечение может достигать очень большой величины
σtot = |
4π Γn . |
|
k 2 Γγ |
У кадмия уровень возбуждения ядра расположен при энергии W0 =0,176эВ, поэтому он является замечательным поглотителем тепловых нейтронов. А именно, полное сечение реакции радиационного захвата Cd113(n,γ )Cd114 с излучением γ -кванта достигает огромной величины 2,5·103барн.
Для многих элементов сечение радиационного захвата теплового нейтрона с испусканием γ -кванта (n,γ ) довольно значительно. В результате
захвата образуется сильно возбужденное составное ядро, которое распадается с испусканием одного или более γ -квантов с общей энергией порядка 8МэВ,
которая характеризует энергию связи нейтрона в тяжелом ядре. Из числа легких химических элементов, входящих в состав биологических тканей, наличие реакции захвата с излучением γ -квантов с энергией 2,2МэВ
установлено для водорода. Незначительная кинетическая энергия теплового нейтрона в случае захвата полностью передается ядру водорода. Энергия отдачи, однако, передается от испускаемых γ -квантов ядру дейтерия, который
получается в результате такой реакции. Из закона сохранения импульса несложно найти энергию отдачи при излучении одного γ -кванта с энергией
Eγ
|
T = p 2 2m = E |
2 2m c2 =533·10-6 A−1E 2 /1МэВ, |
(6.27) |
|||
|
γ |
2 |
γ |
2 |
γ |
|
где p |
= E c - импульс отдачи, |
m - масса мишени после захвата нейтрона. В |
||||
γ |
γ |
|
|
2 |
|
|
рассмотренном примере |
Eγ |
=2,2МэВ, |
поэтому энергия отдачи |
будет |
||
составлять величину порядка 1кэВ, чего более чем достаточно для разрыва химических связей и молекулярных цепочек. Кроме того, вторичные γ -
кванты сами могут создавать комптоновские электроны отдачи с большой энергией порядка 1МэВ.
Такой химический элемент, как азот, также входит в состав многих биологических молекул и может участвовать в захвате медленных и тепловых нейтронов. В результате распада возбужденного ядра N испускается протон

7 N14 + n→6 C14 + p ,
причем неупругие потери Q =– 0,6МэВ, что говорит о достаточно большой
энергии продуктов такой экзотермической реакции. Аналогично (5.27) из закона сохранения импульса получаем выражения
T = |
|
Q |
|
(1+ A) , |
Ep = |
|
Q |
|
A (1+ A) , |
(6.28) |
|
|
|
|
из которых следует, что большую часть энергии после распада уносит протон. Энергии отдачи порядка 40кэВ, которая остается у атома углерода, более чем достаточно для разрыва связей. Получившийся протон отдачи также имеет достаточно большую для создания структурных дефектов энергию. Однако в целом преувеличивать роль ядерных реакций в создании структурных дефектов и в первичном поражении биологических объектов не следует из-за малости соответствующих сечений и большой величины пробега нейтронов
(быстрых и медленных). Например, для 6 C12 в виде графита сечение упругого
ядерного рассеяния нейтронов составляет величину около σ =4,8барн, в то время как сечение поглощения на три порядка меньше: σn =3·10-3барн.
5.6 Потери энергии и затухание пучков γ-излучения
Как уже отмечалось в разделе 3, γ -кванты могут взаимодействовать с
атомами мишени посредством различных механизмов, причем в области энергий Eγ ≤1МэВ связанные с γ -квантами эффекты обусловлены, по
существу, только фотоэлектронами и комптоновскими электронами. Роль эффекта Комптона возрастает с уменьшением зарядового числа, поэтому при всех значениях энергии Eγ ≤50МэВ тормозная способность и пробег γ -
квантов в биологических объектах определяется практически только комптоновским рассеянием. Используя аналитическое выражение (3.35) для дифференциального сечения комптоновского рассеяния можно, в принципе, найти выражение для тормозной способности в случае комптоновского рассеяния γ -квантов. Наиболее просто комптоновское рассеяние выглядит в
приближении жесткой сердцевины, которое применялось выше для описания тормозной способности и линейного пробега при упругом рассеянии быстрых нейтронов. В этом приближении для тормозной способности γ -квантов и
соответствующего линейного пробега при рассеянии формально будут справедливыми соотношения типа (6.23) и (6.24).
Понятно, что на самом деле зависимость тормозной способности от энергии γ -кванта нелинейна. Наиболее просто это можно увидеть в
предельном случае γ -квантов большой энергии, когда ε = Eγ 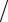 mec2 >>1. Тогда
mec2 >>1. Тогда
непосредственно из выражения (3.35) для дифференциального сечения комптоновского рассеяния γ -квантов и определения тормозной способности
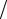
(4.11) получаем
|
dEγ |
|
πr 2 |
Tm |
|
T 2 |
|
2 |
2 |
|
5 |
|
|
− |
|
= n2 z2 |
e |
∫T 2 + |
|
dT =n2 z2πre |
mec |
ln 2ε − |
|
|
. (6.29) |
||
dRL |
ε2mec2 |
|
6 |
||||||||||
|
|
0 |
|
(Eγ −T )Eγ |
|
|
|
|
|
||||
Таким образом, с ростом энергии как полное сечение (3.36), так и тормозная способность комптоновского рассеяния γ -квантов на атомных электронах
возрастает логарифмически. Хотя этот рост не такой большой, как у нейтронов, он существенно отличает γ -кванты от всех заряженных частиц.
Как было показано, для всех тяжелых частиц существует относительно хорошо определенное соотношение между начальной энергией, тормозной способностью и пробегом. В отличие от таких частиц пучок γ -излучения
затухает в конденсированной среде экспоненциально, что связано с необратимой потерей γ -кванта из узкого падающего пучка при первом же
столкновении. В этом смысле к комптоновскому рассеянию γ -квантов
наиболее близко, очевидно, ядерное торможение электронов и позитронов, хотя для этих легких частиц не удается в общем случае получить в аналитическом виде зависимость продольного пробега и функции распределения векторного пробега от начальных параметров частиц. Уменьшение плотности потока γ -квантов при увеличении глубины
пропорционально величине потока Φ(x) , поэтому закон затухания пучка γ -
квантов, как и пучка электронов при определенных условиях, следует экспоненциальному закону (6.19).
После первого рассеяния γ -квант продолжит терять энергию и в конце
концов будет поглощен в результате фотоэффекта каким-либо из атомов мишени. Однако этот процесс уже не влияет собственно на уменьшение числа γ -квантов в узком падающем пучке γ -квантов, поэтому линейный
коэффициент затухания γ -излучения µ = Σc = n2 z2σc = neσc определяется преимущественно макроскопическим сечением комптоновского рассеяния γ - квантов с начальной энергией Eγ . В соответствии с законом (6.19) средний
продольный пробег в данном случае можно определить как такую глубину x = Rp , на которой плотность потока уменьшается в e раз по сравнению с
исходной величиной Φ(0) :
Rp =1 neσc . |
(6.30) |
Несложно видеть, что такое определение в точности совпадает с длиной свободного пробега (см. (1.23)) между актами рассеяния комптоновского типа. При Eγ = 1МэВ, когда σc ≈1барн, типическое значение продольного пробега
равно Rp ≈0,3см в таком, например, материале, как медь, где ne =2,5·1024 см-3. Выше затухание пучка γ -квантов рассматривалось лишь как
