
- •1. ОСНОВНЫЕ ПОНЯТИЯ РАДИАЦИОННОЙ ФИЗИКИ
- •1.1 Ядерные излучения
- •Таблица 1.1
- •Уровни радиобиологических процессов
- •2.1 Пределы классического описания
- •2.4 Борновское приближение
- •2.6 Виды потенциалов взаимодействия
- •3.1 Столкновения электронов с атомами
- •3.2 Релятивистское и квантовое сечения рассеяния электронов
- •3.3 Столкновения тяжелых заряженных частиц с атомами
- •3.4 Кинетика неупругого столкновения тяжелой частицы с атомом
- •3.5 Рассеяние нейтронов на атомах
- •Задачи
- •4.1 Внешнее и внутреннее облучение
- •4.2 Виды пробегов частиц
- •4.3 Распределение векторных пробегов
- •4.4 Тормозная способность
- •4.5 Флуктуации потерь энергии частицы
- •Задачи
- •5.1 Торможение тяжелых ионов
- •5.2 Электронное торможение ионов
- •5.3 Ядерное торможение тяжелых ионов
- •Алюминий
- •Свинец
- •5.4 Пробег тяжелых ионов
- •Задачи
- •6.1 Рассеяние Мотта и потери энергии быстрых электронов
- •6.2 Разброс энергий и пробегов при многократном рассеянии электрона
- •6.4 Пробег и потери энергии нейтронов
- •Задачи
- •7.2 Образование и устойчивость дефектов в кристаллах
- •7.4 Каскадная функция
- •7.5 Пространственное распределение дефектов в каскаде
- •7.6 Полное число дефектов
- •8.1 Физические основы дозиметрии
- •7.2 Эквивалентная доза
- •7.4 Принципы попадания и мишени в радиобиологии
- •8.5 Другие физические модели
Е.А.Баранник
ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЙ С ВЕЩЕСТВОМ
УЧЕБНОЕ ПОСОБИЕ
ВВЕДЕНИЕ
Облучение тел и жидкостей как биологического, так и небиологического происхождения может приводить к изменению их физико-химических свойств, которое в нативных биологических объектах сопровождается, как правило, и изменением функционального состояния. Некоторые эффекты такого рода были обнаружены еще до появления мощных источников излучения и открытий в ядерной физике, давших толчок к развитию ядерной энергетики и исследованию взаимодействия излучений с веществом. В настоящее время целью исследований в этой области все чаще становится, например, создание материалов с заданными физико-химическими свойствами, удовлетворяющими тем высоким требованиям, которые предъявляются в медицине. Другим важным примером медицинского применения радиационных технологий может служить использование ионизирующих и неионизирующих излучений в диагностике и хирургии. В этом смысле настоящее учебное пособие является необходимым для дальнейшего изучения радиационных направлений медицинского материаловедения, а также для понимания первичных факторов радиационного поражения биологических и небиологических объектов, которые на физическом уровне и в рамках физических моделей определяют радиационные процессы и радиобиологические эффекты.
Чтобы понять первичные физические изменения, возникающие в конденсированных средах под действием облучения, необходимо детально ознакомиться с наиболее важными явлениями, индуцируемыми различными видами радиации в атомной и молекулярной структуре вещества. Большинство физических явлений, о которых будет идти речь при рассмотрении процесса прохождения излучения через вещество, можно свести в своей основе к отдельным столкновениям между двумя свободно движущимися телами, например, бомбардирующим ионом и атомом вещества. Краткому рассмотрению (классическому и квантовому) взаимодействия между частицами излучения и частицами конденсированной среды, а также описанию места предлагаемого материала в общей модели радиационных и радиобиологических процессов, посвящена вспомогательная часть курса, включая Приложения.
В основной части курса речь идет о конкретных типах излучений, которые являются наиболее распространенными при использовании в разнообразных лучевых медицинских технологиях и наиболее важными с точки зрения радиобиологии. В соответствии с этим достаточно большое внимание уделяется физике взаимодействия различных излучений при столкновениях и рассеянии на атомах вещества, которые приводят в конечном итоге к образованию структурных дефектов и других первичных повреждений.
Обсуждаются вопросы, связанные с изменением характеристик частиц излучения в процессе взаимодействия с атомами вещества и эффективностью этого взаимодействия, что важно, например, для понимания физических основ дозиметрии. Из числа параметров облучаемых структур, определяющих первичные физические эффекты, основное внимание уделяется тем, которые являются общими при описании изменения физико-химических свойств биологических и небиологических объектов. Интересной особенностью здесь является то, что само рассмотрение и некоторые важные выводы могут быть сделаны без учета симметрии и степени регулярности молекулярной структуры облучаемого вещества. Это позволяет использовать многие результаты, полученные в радиационном материаловедении, для пояснения физических основ радиобиологии и дозиметрии.
В зависимости от подготовки самостоятельное изучение материала можно начинать либо с Приложения, либо непосредственно с раздела 1, который открывает основную часть курса, рассчитанную на 54 часа учебного времени. Необходимо подчеркнуть, что основной курс требует достаточно полного знания основ классической и релятивистской механики, а также квантовой физики. При формировании содержания основной части настоящего курса, предназначенного для студентов по специальностям «медицинская физика» и «биофизика», и методологии его изложения решались две задачи.
Первой из них было более полное по сравнению с известными учебниками и пособиями по радиационной биофизике и радиобиологии, приведенными в списке рекомендованной литературы, физическое обоснование первичных эффектов, наблюдаемых в биологических объектах. Дело в том, что многие из этих эффектов можно достаточно уверенно интерпретировать, опираясь непосредственно на традиционные для радиационной физики подходы. С другой стороны, ставилась цель показать в деталях, как из основных положений ядерной и радиационной физики вытекают физические модели и численные оценки, которые могут непосредственно применяться при описании радиобиологических эффектов и построении моделей радиационной биофизики. С этой точки зрения указанные в списке рекомендованной литературы источники следует рассматривать как вспомогательный материал, который может дополнить содержание данного пособия в сторону большей детализации ядерно-физических либо радиобиологических и биофизических аспектов взаимодействия излучений с биологическими объектами. Учебное пособие может быть полезным как для тех, кто изучает этот предмет впервые, так и для широкого круга специалистов, которые желают усовершенствовать свои знания в этой междисциплинарной области знаний за счет более уверенного применения известных физических закономерностей и подходов.
Автор выражает глубокую признательность Г.П. Горбенко, которая прочитала рукопись учебного пособия и сделала ряд ценных замечаний, а также Ю.А. Бережному за важные советы и обсуждение математических вопросов ядерной физики и квантовой механики. Автор благодарен также издательскому отделу Харьковского национального университета имени В.Н. Каразина за помощь в подготовке к печати учебного пособия.
1. ОСНОВНЫЕ ПОНЯТИЯ РАДИАЦИОННОЙ ФИЗИКИ
1.1 Ядерные излучения
Изложение курса целесообразно начать с краткого описания различных видов ядерных излучений и пояснения того места, которое излагаемый материал занимает в общей модели всех процессов, индуцированных внешними излучениями. Как известно, при радиоактивном распаде из ядер вылетают α -частицы, электроны, нейтрино и γ -кванты. Потоки испускаемых
при радиоактивном распаде частиц называют радиоактивным излучением. Радиоактивный распад – не единственный источник быстрых частиц. Космическое пространство также пронизано потоками различных частиц – протонов, α -частиц, ядер более тяжелых элементов, электронов, фотонов и т.д., энергии которых в такого рода космическом излучении достигают порой значений вплоть до 1020эВ (1Дж = 6,24·1018эВ). Далее, мощные потоки быстрых заряженных частиц получают с помощью ускорителей. Источником различных частиц, в том числе нейтронов, являются также ядерные реакторы. При взаимодействии быстрых ультрарелятивистских частиц с веществом возникает множество новых метастабильных частиц – мезонов, гиперонов и др. Потоки всех перечисленных выше частиц, возникающих при естественных процессах и получаемых искусственно, объединяют общим названием
ядерного излучения.
Проходя через вещество, все виды ядерного излучения так или иначе взаимодействуют с ним, причем характер этого взаимодействия зависит не только от свойств вещества, но и от типа излучения, энергии частиц и т.д. Заряженные частицы – электроны, позитроны, мезоны, протоны, ядра гелия и более тяжелых элементов, а также γ -кванты взаимодействуют с электронами
атомных оболочек и ядрами встречных атомов главным образом посредством электромагнитных взаимодействий. При близких столкновениях с ядрами тяжелых частиц, в том числе и нейтронов, проявляются силы ядерного (сильного) взаимодействия. Кроме того, все частицы, кроме γ -кванта,
участвуют в так называемом слабом взаимодействии. Все эти виды взаимодействия имеют разную природу и порядок величины, о котором можно судить по сечению рассеяния. Ядерные силы при непосредственном взаимодействии характеризуются сечениями порядка 10-27-10-24см2 и малыми временами 10-23-10-21с процессов распада. Электромагнитные взаимодействия в 100-1000 раз слабее ядерных и во столько же раз медленнее (10-20-10-18с), однако имеют дальнодействующий характер и относятся к числу наиболее распространенных в природе. Примером слабых взаимодействий является β -
распад, который приводит, например, к нестабильности нуклонов. Слабые взаимодействия в 1013 раз слабее сильных, поэтому при прохождении частиц
через вещество их влиянием можно пренебречь.
Различные взаимодействия по-разному проявляются для внешнего наблюдателя. Например, в результате процессов сильного взаимодействия ядерноактивные частицы эффективно поглощаются и выбывают из коллимированного пучка при прохождении через среду. К проявлениям электромагнитных взаимодействий относятся кулоновское рассеяние, ионизационное торможение, радиационное торможение, черенковское излучение, фотоэффект, образование электрон-позитронных пар и т.д. Общим для всех видов взаимодействия ядерного излучения с веществом является то, что энергия падающих частиц передается атомам вещества, а поле излучения меняет свои параметры по мере прохождения через вещество. Последнее обстоятельство является, например, физической основой для создания различных методов медицинской диагностики.
Передаваемая веществу энергия затрачивается, в частности, на возбуждение и ионизацию атомов среды. Поэтому ядерное излучение является одной из разновидностей ионизирующего излучения, к которому относятся также ультрафиолетовое излучение, рентгеновское излучение и некоторые другие. Процессы, типа ионизации вещества, приводят к различным эффектам (например, потемнение фотопластинки), лежащим в основе многих методов регистрации ионизирующих излучений. Некоторые из эффектов, индуцированных под действием излучения в живых организмах, могут существенно нарушить процессы жизнедеятельности, что является предметом изучения в радиобиологии. С другой стороны, по мере углубления в среду интенсивность излучения уменьшается, в результате чего слои вещества могут служить защитой от ядерного излучения.
1.2 Уровни радиационных и радиобиологических процессов
При описании уровней радиобиологических процессов необходимо сразу отметить, что в отличие от объектов неживой природы, облучение биологических объектов может приводить не только к изменению их структуры и химического состава, но и изменению связанных с ними чрезвычайно важных функциональных свойств. Поэтому при создании теоретических моделей, способных объяснить и предсказать весьма широкий круг наблюдаемых радиобиологических явлений, необходимо использовать системный многоуровневый подход. Этот системный подход опирается на сложную иерархическую внутреннюю структуру биологических объектов и учитывает, что процессы после облучения протекают качественно по-разному на различных уровнях организации живого. В соответствии со структурой и организацией биологических объектов можно использовать систему уровней радиационных и радиобиологических эффектов, которая представлена в Таблице 1.1.
Из таблицы видно, что время протекания процессов на разных уровнях

|
|
Таблица 1.1 |
|
Уровни радиобиологических процессов |
|
|
|
|
Уровень |
Время |
Процессы, протекающие на данном уровне; |
протекания, с |
возможность модификации |
|
Физический 10-18-10-13
Химический 10-14-10-4
Биохимический (субклеточный) 10-4-105
Биологический 103-107
(клеточный)
Упругие и неупругие столкновения →
ионизация, возбуждение, релаксация и термализация, образование структурных дефектов, высокореактивных радикалов макромолекул и короткоживущих свободных радикалов воды; модификация отсутствует
Реакция свободных радикалов друг с другом, с
ДНК, белками и клеточными органеллами → образование первичных повреждений под действием радикалов (повреждение оснований, димеризация и т.д.); модификация радиопротекторами, кислородом, температурой
Репарация, взаимодействие повреждений →
образование конечных нерепарируемых повреждений (мутаций, аберраций и др.); модификация температурой и другими агентами
Деление и гибель клеток, изменение их свойств
в результате мутаций
значительно отличается по длительности. Поэтому вполне оправданно считать, что процессы на более низком уровне независимы от процессов на более высоком уровне и начинаются на более высоком тогда, когда на более низком они уже в основном закончились. Это первый важный вывод, который можно сделать при системном подходе к моделированию радиационных эффектов в биологических объектах.
Понятно, что любые изменения в биологических объектах под действием излучений связаны с передачей энергии, хотя сама по себе передача энергии не всегда, как будет показано далее, приводит к изменениям в биологических объектах. При корректном физическом рассмотрении процессов рассеяния, сопровождающих упругие и неупругие столкновения частиц, и использовании аппарата математической статистики можно, в принципе, рассчитать вероятность распределения событий передачи энергии налетающих частиц и ее величину за счет всех физических механизмов торможения (упругие и неупругие атомные столкновения, ионизация и возбуждение атомов и т.д.) в биологическом объекте. Знание таких распределений и физических характеристик закладывает основу для определения величины эффектов на следующем химическом уровне. Эта
возможность подкрепляется также наличием огромного экспериментального материала о взаимодействии излучений разного типа с веществом, включая различные биологические объекты и среды. Главная же задача на физическом уровне состоит в том, чтобы с помощью расчетных и экспериментальных данных получить количественную информацию о среднем результирующем выходе структурных дефектов и свободных радикалов при прохождении излучения через данную биологическую среду.
В общем случае с использованием этой информации на следующем химическом уровне необходимо постулировать, во-первых, какие повреждения – структурные и обусловленные свободными радикалами, являются решающими в формировании конечного эффекта, а какими из них можно пренебречь. Такие постулаты для каждого объекта являются результатом как теоретических оценок, так и экспериментальных исследований. Во-вторых, в радиобиологических моделях на химическом уровне необходимо с максимальной полнотой учесть влияние короткоживущих свободных радикалов, а также кислорода и других модификаторов на выход первичных повреждений, связанных с радикалами. При этом радиобиологическая модель действия излучений на химическом уровне должна оперировать количественными связями между выходом всех первичных повреждений и исходными характеристиками, установленными на физическом уровне. Это дает определенные возможности для экспериментальной проверки как заложенных постулатов, так и использованных количественных соотношений.
На биохимическом уровне модель должна учитывать процессы репарации, взаимодействия первичных повреждений и другие возможные процессы. При этом выход конечных повреждений на субклеточном уровне, например, мутаций, зависит только от числа, спектра и распределения всех первичных повреждений внутри клетки. В этом смысле безразлично, каким образом возникли первичные повреждения – при прямом действии излучения или под действием образовавшихся химических агентов. Поэтому на биохимическом уровне модель и соответствующие математические уравнения могут, вообще говоря, отражать связь с физическими характеристиками не только посредством первичных повреждений, возникших на химическом уровне.
Наконец, на клеточном уровне модель должна выражать связь между вероятностью гибели клетки и конечными повреждениями в клетке. В частности, генетические повреждения формируются на биохимическом уровне. Однако проявляются такие эффекты и на более высоких уровнях – на клеточном для бактерий и других одноклеточных объектов и на организменном для многоклеточных объектов. На клеточном уровне генетический эффект проявится в том случае, если в клетке произойдет нелетальная мутация. В многоклеточном организме эта клетка должна быть еще и родоначальной (половой) клеткой, зародышем нового организма.
Таким образом, последовательное моделирование радиобиологических эффектов в биологических объектах включает в себя:
1.Рассмотрение всех радиобиологических уровней, при котором каждому уровню ставится в соответствие своя модель, описывающая и предсказывающая величину конечного эффекта на этом уровне. При построении модели радиобиологического уровня используют известные эмпирические закономерности и количественные связи.
2.Учет факта взаимосвязи уровней – в идеальном случае величина биологического эффекта на данном уровне однозначно выражается через величину эффекта на более низком уровне. Связь величины эффекта на данном уровне с физическими параметрами должна устанавливаться с учетом уровней, лежащих между физическим и данным.
3.Получение конечной модели, имеющей предсказательный характер и позволяющей после экспериментального уточнения принятых постулатов и количественных соотношений для данного биологического объекта прогнозировать конечный радиобиологический эффект в объекте при действии излучения с известными характеристиками.
Из сказанного следует, что при оценке действия излучения уже на химическом уровне необходимо использовать результаты, которые вытекают из модельных представлений об образовании структурных дефектов и радикалов, связанных с передачей энергии на физическом уровне. Важно подчеркнуть, что само по себе описание радиационных эффектов на физическом уровне ничем не отличается для биологических и небиологических объектов и сред. Это дает возможность использовать общефизические подходы, развитые, например, для исследования взаимодействия излучения с конденсированной средой, в частности, с твердым телом. Ключевыми физическими характеристиками здесь являются сечение рассеяния, тормозная способность частицы, которую в радиобиологии
ирадиационной биофизике часто называют линейной передачей энергии, поглощенная доза, а также макро- и микродозиметрическое распределение. Описанию физического уровня радиационных процессов вообще и некоторых радиобиологических эффектов в частности посвящена основная часть материала курса.
Вобщем случае, как отмечалось выше, действие излучений на химическом уровне характеризуется числом и спектром всех первичных повреждений, выход которых зависит от физического уровня. С одной стороны, это позволяет установить некоторые общие соотношения, нужные для понимания физических основ дозиметрии. Применительно же к биологическим объектам выбор физико-математической модели на этом уровне в значительной степени зависит от объекта. Например, для малых вирусов и фагов достаточно ввести модельное представление о чувствительном или радиочувствительном объеме, который в самом первом
приближении просто равен объему объекта. Предполагается, что вызвать
первичное повреждение и гибель вируса или фага способны только события передачи энергии, состоявшиеся в этом объеме. Исходными физическими характеристиками при этом являются поглощенная доза и качество излучения, которые определяют выживаемость таких объектов. Здесь действие излучений на химическом уровне – конечный эффект, в то время как для клеток млекопитающих первичные повреждения не являются, очевидно, конечными эффектами. Аналогичным образом, химический уровень является конечным и для неорганических веществ, в частности, для твердых тел. Это обстоятельство позволяет связать конечные радиобиологические эффекты для малых вирусов и фагов непосредственно с физическим уровнем при помощи так называемых физических моделей, которые кратко описываются в последней части курса.
1.3 Дифференциальное сечение рассеяния
Рассеяние частицей-мишенью отдельной налетающей частицы достаточно подробно рассмотрено в Приложении. Это рассмотрение показывает, что как при классическом, так и релятивистском описании начальная энергия налетающей частицы, прицельное расстояние и потенциал взаимодействия между частицами полностью определяют их характеристики, например, конечные импульсы и энергии после столкновения.
В общем случае невозможно, однако, проследить за отдельным процессом рассеяния, поскольку для реальных излучений и в реальных экспериментах по рассеянию приходится иметь дело со множеством налетающих частиц, например, с пучком падающих моноэнергетических частиц. Кроме того, для процессов взаимодействия и, в частности, процессов рассеяния, происходящих при облучении конденсированных сред – биологических объектов, жидкостей, твердых тел и т.д., необходимо учитывать все частицы-мишени вещества. Ими могут быть, например, различные атомы макромолекул и молекулярных комплексов, если речь идет о биологических объектах, или атомы твердого тела, выбиваемые из узлов решетки. При этом даже для атомов одного сорта в мишени нельзя говорить, очевидно, о единственном прицельном расстоянии и, следовательно, о заданном угле рассеяния и переданной энергии. Задача в этом случае состоит в том, чтобы с использованием известных законов, описывающих элементарный акт рассеяния при разных начальных условиях, получить соотношение между распределением прицельных расстояний и распределением углов рассеяния. Это возможно, если учесть известную зависимость (П.24) угла рассеяния от прицельного расстояния, найденную для единичного акта рассеяния.
Наиболее простым является, очевидно, случай падения на мишень однородного параллельного пучка тождественных моноэнергетических
частиц. Величина плотности потока для однородного пучка частиц описывается при помощи простого соотношения
Φ = nv , |
(1.1) |
где n - пространственная плотность налетающих частиц, имеющих одинаковую по направлению скорость v . Непосредственно из размерности плотности потока (1.1) вытекает, что эта величина представляет собой число частиц, пересекающих за 1с площадку с единичной площадью, перпендикулярную к направлению падения. Интегральным потоком или флюенсом называют интеграл
t
Φ = ∫Φ(t)dt ,
0
который показывает полное число частиц, прошедших за время экспозиции t через единичную площадку. Если поток не зависит от времени, то Φ = nvt .
Понятие о дифференциальном сечении рассеяния вводят для описания распределения углов рассеяния. Рассмотрение снова начнем с относительной системы отсчета, где налетающая частица с приведенной массой µ
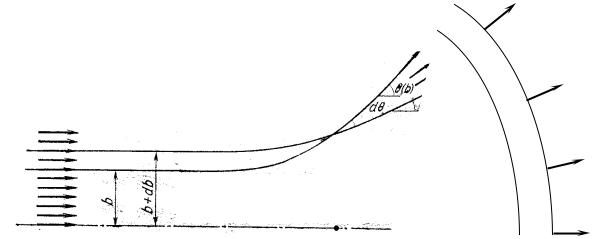
взаимодействует с силовым центром в виде всегда неподвижной частицымишени. Процесс рассеяния пучка в одной из орбитальных плоскостей движения изображен на рис.1.1. По-прежнему ограничимся рассмотрением случая сферически симметричного силового поля, при котором потенциал взаимодействия между сталкивающимися частицами зависит исключительно от относительного расстояния между ними. Тогда изображенное на рис.1.1 распределение налетающих частиц в однородном пучке и пространственное распределение траекторий рассеянных частиц являются аксиальносимметричными с осью, параллельной направлению налетающих частиц и проходящей через мишень. Вращение вокруг этой оси будем задавать при помощи угла α .
k
v
Рис.1.1 Распределение траекторий движения при рассеянии налетающих частиц неподвижной мишенью в относительной системе отсчета.
В соответствии с определением (1.1) число частиц, пролетающих за 1с через кольцевую площадку, заключенную между окружностями с радиусами (прицельными расстояниями) b и b + db, равно произведению плотности потока на площадь кольца: Φ2πbdb . С другой стороны, при однозначной зависимости угла рассеяния от прицельного расстояния все эти частицы за 1с должны появиться после столкновения в телесном угле dΩ между двумя конусами с углами раскрытия ϑ(b) и ϑ(b + db) ≈ϑ(b) + dϑ. Благодаря этому
можно записать равенство
Φ2πbdb = Φσ(ϑ)dΩ ≡ Φdσ , |
(1.2) |
где величина σ(ϑ) есть дифференциальное сечение рассеяния, которое играет
роль коэффициента пропорциональности в (1.2), а величина dσ называется
эффективным сечением рассеяния. Эти сечения зависят от вида взаимодействия и имеют размерность площади.
Непосредственно из определения (1.2) следует, что чем больше величина σ(ϑ) , тем меньше при заданных параметрах налетающих частиц
будет телесный угол dΩ и соответственно, тем больше частиц для данного вида взаимодействия будет рассеиваться в направлении ϑ . Величину σ(ϑ)
можно считать, таким образом, мерой плотности вероятности для рассеяния в заданном направлении ϑ или функцией распределения углов, на которые рассеиваются налетающие частицы из однородного параллельного пучка. Подчеркнем, что функция σ(ϑ) однозначно определяется законом рассеяния
для данного вида взаимодействия между налетающей частицей и мишенью. Эта важная и часто используемая при описании процесса рассеяния величина содержит всю информацию о рассеянии пучков частиц, поэтому задача о рассеянии сводится теперь к вычислению величины σ(ϑ) .
При квантовомеханическом описании рассеяния волновые функции рассеянных частиц на больших расстояниях представляют собой сферически
расходящиеся волны с волновым вектором k = k r r , направленным в каждой
r , направленным в каждой
точке вдоль радиус вектора r (см. рис.1.1). Поэтому число частиц, рассеивающихся за секунду в телесный угол dΩ, удобнее всего выразить через радиальную компоненту плотности потока Φr (r) . А именно, число
частиц, пролетающих за 1с через кольцевую площадку, равно числу частиц,
пролетающих за 1с через площадь r2dΩ, которую поток пересекает на большом расстоянии от рассеивающего центра:
Φ2πbdb = Φσ(ϑ)dΩ = Φr (r)r2dΩ. |
(1.3) |
С учетом цилиндрической симметрии распределения частиц телесный угол можно записать в виде dΩ = 2π sinϑdϑ , поэтому из соотношения (1.2) получаем простую формулу
dσ |
=σ(ϑ) = |
b |
|
|
db |
|
, |
(1.4) |
|
|
|||||||
dΩ |
sinϑ |
|
dϑ |
|||||
|
|
|
|
|
||||
которая и поясняет определение “дифференциальное сечение”. Выражение (1.4) дает зависимость дифференциального сечения от прицельного расстояния и начальной энергии падающих частиц, поскольку от этой величины зависит угол рассеяния. Кроме того, в выражении (1.4) обычно пишут абсолютное значение производной db dϑ , поскольку она, как правило,
dϑ , поскольку она, как правило,
отрицательна для потенциалов отталкивания и положительно определенных углов рассеяния, в то время как дифференциальное сечение рассеяния всегда вводят как величину положительную.
Как показано в Приложении, зависимость прицельного расстояния от угла рассеяния b(ϑ) может оказаться неоднозначной, как в случае потенциала,
соответствующего притяжению и отталкиванию для разных прицельных расстояний (см. комментарий к рис.П.2). В этом случае в соотношении (1.3) необходимо вместо произведения bdb использовать сумму произведений bi dbi
по всем ветвям многозначной функции b(ϑ) для одного и того же интервала углов рассеяния. В результате формула (1.4) записывается через сумму
dσ |
=σ(ϑ) = |
1 |
∑b |
|
dbi |
|
, |
(1.5) |
|
|
|
||||||||
dΩ |
sinϑ |
||||||||
|
i i |
|
dϑ |
|
|
|
поскольку частицы с различными прицельными расстояниями и одинаковым по модулю углом рассеяния вносят положительный вклад в интенсивность рассеяния в заданном направлении ϑ . Например, дифференциальное сечение рассеяния для случая, показанного на рис.П.2, имеет вид суммы следующих абсолютных значений
σ(ϑ) = |
1 |
b (ϑ) |
|
db1 (ϑ) |
|
+b |
(−ϑ) |
|
db2 (−ϑ) |
|
+b |
(−ϑ) |
|
db3 (−ϑ) |
|
|
, |
|||
|
|
|
|
|
|
|||||||||||||||
|
||||||||||||||||||||
|
sin |
|
|
1 |
|
dϑ |
|
2 |
|
|
dϑ |
|
3 |
|
|
dϑ |
|
|
|
|
|
ϑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где угол рассеяния 0 ≤ϑ ≤π .
1.4 Сечения рассеяния в лабораторной системе координат
Дифференциальное сечение рассеяния σ(ϑ) в относительной системе
отсчета, где частица-мишень все время неподвижна, позволяет легко определить дифференциальное сечение рассеяния σ(ϑ1 ) налетающей частицы
в лабораторной системе, в которой частица-мишень покоится только до столкновения. Главное соображение сводится к тому, что число рассеивающихся частиц не может зависеть от системы отсчета. Поэтому число частиц, рассеивающихся в телесный угол dΩ1 = 2π sinϑ1dϑ1 около направления
ϑ1 в лабораторной системе, должно совпадать с числом частиц,
рассеивающихся в телесный угол dΩ = 2π sinϑdϑ около направления ϑ в относительной системе и в системе центра инерции, поскольку в соответствии с (П.28) углы рассеяния в системе центра инерции и в относительной системе
отсчета совпадают. Тогда при однозначном соответствии между ϑ1 |
и ϑ можно |
||||||||
по аналогии с выводом соотношения (1.4) воспользоваться равенством |
|||||||||
|
σ(ϑ1 )sinϑ1dϑ1 =σ(ϑ)sinϑdϑ. |
(1.6) |
|||||||
Отсюда для положительно определенных углов находим |
|
||||||||
σ(ϑ ) =σ(ϑ) sinϑ |
|
dϑ |
|
|
d(cosϑ) |
|
|
(1.7) |
|
|
|
=σ(ϑ) |
|
, |
|||||
|
|
|
|
||||||
1 |
sinϑ1 |
dϑ1 |
|
|
d(cosϑ1 ) |
|
|
||
|
|
|
|
|
|||||
где σ(ϑ1 ) и σ(ϑ) представляют собой разные функции и потому их следовало
бы, строго говоря, различать при помощи разных символов или индексов, обозначающих систему отсчета. Тем не менее сечения рассеяния в разных системах отсчета и дальше будут отличаться только аргументом.
Из результатов рассмотрения, проведенного в Приложении, вытекает неоднозначная в некоторых случаях зависимость ϑ от ϑ1 . Явный вид этой
зависимости можно получить путем подстановки выражения (П.38) в (П.40):
|
m1 |
|
|
|
|
|
|
2 |
|
|
|
1 2 |
|
cosϑ± = − |
sin |
2 |
ϑ1 |
± cosϑ1 |
1 |
m1 |
|
sin |
2 |
ϑ1 |
. |
(1.8) |
|
m2 |
|
− |
|
|
|||||||||
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как отмечалось в пояснениях к формуле (П.40), только при m1 ≤ m2 решение является однозначным и соответствует значению ϑ+ . Именно это решение стремится к нулю при ϑ1 → 0 , как это и должно быть в соответствии с
векторной диаграммой рассеяния на рис.П.4. Поэтому в выражение (1.7) при m1 ≤ m2 следует подставлять значение ϑ+ , что дает
|
|
|
|
|
m2 ) |
|
cos 2ϑ1 |
|
(1.9) |
σ(ϑ1 ) =σ(ϑ+ ) d(cosϑ+ ) =σ(ϑ+ ) 2 m1 cosϑ1 + 1+ (m1 |
2 |
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
d(cosϑ1 ) |
m2 |
|
|
|
|
|||
|
|
[1−(m1 |
m2 )2 sin2 ϑ1 ]1 2 |
|
|
||||
где 0 ≤ϑ1 ≤π . |
|
|
|
|
|
|
|
|
|
При m1 > m2 |
необходимо учесть оба корня, поскольку рассеяние в обоих |
||||||||
направлениях ϑ+ |
и ϑ− в относительной системе отсчета дает положительный |
||||||||
вклад в рассеяние под углом ϑ1 |
в лабораторной системе отсчета. Как видно из |
||||||||
рис.П.4, эти рассеяния отличаются тем, что при увеличении угла ϑ1 |
угол ϑ+ |
||||||||
возрастает, а ϑ− |
– убывает, |
в результате |
чего производная dϑ− |
dϑ1 |
< 0 . |
||||
Поскольку вклад в дифференциальное сечение рассеяния дает сумма абсолютных значений, то слагаемое с производной от ϑ− нужно взять со
знаком минус. Тогда получаем выражение

σ(ϑ ) =σ(ϑ |
) d(cosϑ+ ) |
−σ(ϑ |
) d(cosϑ− ) |
, |
|
1 |
+ |
d(cosϑ ) |
− |
d(cosϑ ) |
|
|
|
1 |
|
1 |
|
которое с учетом соотношения (1.8) преобразуется к виду
|
cosϑ1 + 1+ (m1 |
m2 ) |
|
cos 2ϑ1 |
|
− |
|
|
|
||
σ(ϑ1 ) =σ(ϑ+ ) 2 m1 |
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
|||
|
[1−(m1 |
m2 )2 sin2 ϑ1 ]1 2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1+ (m1 |
m2 ) cos 2ϑ1 |
|
||||
|
−σ(ϑ− ) 2 m1 cosϑ1 |
− |
|
, (1.10) |
|||||||
|
|
m2 )2 sin2 ϑ1 ]1 2 |
|||||||||
|
|
m2 |
|
|
[1−(m1 |
|
|
||||
где 0 ≤ϑ1 = arcsin(m2 / m1 ) . Отметим, что в правых частях формул (1.9) и (1.10) сечения σ(ϑ± ) берутся для углов ϑ± (1.8), выраженных явно через угол ϑ1 .
Аналогичным образом получается сечение отдачи или распределение σ(ϑ2 ) углов рассеяния ϑ2 для частицы-мишени в лабораторной системе. Связь
между углами ϑ и ϑ2 всегда однозначна и описывается простым выражением (П.37): ϑ =π − 2ϑ2 , поэтому при произвольном отношении масс налетающей частицы и мишени находим
σ(ϑ2 ) =σ(ϑ) |
d(cosϑ) |
|
= 4σ(ϑ)cosϑ2 , |
(1.11) |
|
d(cosϑ2 ) |
|||||
|
|
|
|
где 0 ≤ϑ2 ≤π 2 .
2 .
Как отмечалось выше, угол рассеяния ϑ в относительной системе и системе центра инерции изменяется во всем интервале от 0 до π независимо от отношения масс, поэтому часто удобно выражать сечение рассеяния в лабораторной системе отсчета через угол рассеяния ϑ в относительной системе. В этом представлении не возникает проблемы двузначности функции ϑ от угла рассеяния ϑ1 при m1 > m2 . Тогда при помощи выражений (П.37)
формула (1.7) преобразуется к виду
σ(ϑ1 (ϑ)) =σ(ϑ) |
d(cosϑ) |
|
=σ(ϑ) |
{1+ (m m )2 + 2(m |
m )cosϑ}3 2 |
, (1.12) |
||||
|
|
1 |
2 |
1 |
2 |
|
|
|||
|
|
|
|
|
|
|
||||
|
d(cosϑ1 ) |
|
|
|
1+ (m1 |
m2 )cosϑ |
|
|
|
|
|
|
|
|
|
|
|||||
а формула (1.11) запишется в виде
σ(ϑ2 (ϑ)) =σ(ϑ) |
d(cosϑ) |
|
=σ(ϑ)4sin |
ϑ . |
(1.13) |
|
d(cosϑ2 ) |
||||||
|
|
|
2 |
|
Рассмотренная картина одновременного взаимодействия пучка многих налетающих частиц с единственной частицей-мишенью, как показано на рис.1.1, эквивалентна множеству независимых отдельных столкновений налетающей частицы с мишенью. Поэтому в проведенных преобразованиях для сталкивающихся частиц фактически подразумевается, что плотность и полное число как налетающих частиц, так и частиц-мишеней незначительны,
поэтому каждая частица участвует в столкновении самое большее один раз. В этом случае действительно можно считать, что частица-мишень не увлекается падающим пучком волн, так что рассеяние происходит каждый раз на неподвижной мишени. Заметим также, что преобразование дифференциального сечения рассеяния в относительной системе отсчета к любой другой инерциальной системе можно выполнить с помощью того же условия сохранения числа частиц, аналогичного (1.6).
Это условие сохранения числа частиц является основополагающим и при более общем рассмотрении понятия сечения рассеяния, которое не следует обязательно связывать с описанием распределения углов рассеяния в разных системах отсчета. С помощью известной функции σ(ϑ) , дающей
угловое распределение в процессе рассеяния при наблюдении в системе центра инерции и относительной системе, можно получить распределение любой другой физической величины, которая связана с углом рассеяния. Это может быть, например, энергия отдачи, конечные импульсы частиц, их скорость и т.д.. Если в качестве такой величины выбрать, например, энергию отдачи или конечную энергию частицы-мишени E2′, то при заданной
начальной энергии налетающих частиц E1 из равенства числа рассеянных и
рассеивающих частиц по аналогии с выражением (1.6) можно записать равенство
σ(E2′; E1 )dE2′ =σ(ϑ)dΩ, |
(1.14) |
где величина σ(E2′; E1 ) представляет собой дифференциальное сечение для частицы-мишени, обладающей после столкновения энергией E2′ = p′2 2  2m2 .
2m2 .
Однозначная зависимость энергии E2′ от угла рассеяния ϑ описывается выражением (П.39), которое имеет вид
E2′ = E2′max sin2 (ϑ 2) .
2) .
Поэтому из равенства (1.14) несложно получить явное выражение для распределения частиц-мишеней по конечной энергии:
σ(E2′; E1 ) =σ(ϑ) |
dΩ |
=σ(ϑ) |
4π |
, |
(1.15) |
dE2′ |
|
||||
|
|
E2′,max |
|
||
где 0 ≤ E2′ ≤ E2′max и E2′max = 4m1m2 E1 / M 2 . Непосредственно из выражений (1.14) и (1.15) следует, что дифференциальное сечение рассеяния σ(E2′; E1 ) имеет
размерность площади, деленной на энергию, тогда как размерность σ(ϑ) – это площадь, деленная на безразмерный телесный угол. Величину σ(E2′; E1 )
называют дифференциальным сечением передачи энергии, а также дифференциальным сечением отдачи, энергетическим спектром частицмишеней и энергетическим спектром отдачи.
Дифференциальное сечение передачи энергии σ(E2′; E1 ) можно выразить

через любую другую переменную, эквивалентную ϑ , если применить соответствующее условие равенства числа рассеянных частиц. В частности, зависимость от угла рассеяния ϑ2 получается из равенства
σ(E2′; E1 )dE2′ =σ(ϑ2 )dΩ2 ,
которое с учетом равенства (П.42)
E2′ = E2′max cos2 ϑ2
приобретает вид
|
|
|
dΩ2 |
|
|
|
π |
|
|
π |
|
E2′ |
1 2 |
|
σ(E′; E ) =σ(ϑ |
) |
=σ(ϑ |
)cosϑ |
|
=σ(ϑ |
) |
|
. |
(1.16) |
|||||
′ |
|
′ |
|
′ |
||||||||||
2 1 |
2 |
|
2 |
|
2 |
2 |
|
′ |
|
|
||||
|
|
|
dE2 |
|
|
|
E2,max |
|
|
E2 |
|
E2,max |
|
|
Аналогичным образом можно найти распределения для других величин, включая векторные, например, для конечного импульса частиц-мишеней, однако для дальнейшего изложения приведенных данных вполне достаточно.
1.5 Полное и парциальные сечения
Понятие дифференциального сечения можно обобщить на любые процессы, происходящие при столкновении двух частиц, и описывать с его помощью, например, неупругие столкновения между атомами, приводящие к возбуждению или выбиванию атомных электронов, ядерные реакции деления и захвата, образование электрон-позитронных пар и любых других комплексов, а также столкновения, приводящие к химическим реакциям. Для этого необходимо только ввести в сечение рассеяния характерные для данного процесса переменные. В связи с множественностью возможных физических процессов, возникающих при столкновениях частиц, понятия о полном и парциальных сечениях рассеяния появляются самым естественным образом. Тем не менее их рассмотрение начнем с самого простого случая единственного механизма взаимодействия, который описывается определенным дифференциальным сечением σ(ϑ) .
Интегрируя дифференциальное сечение по всему телесному углу, получаем полное сечение рассеяния для данного вида взаимодействия
|
π |
|
σ(E1 ) = ∫σ(ϑ)dΩ = 2π ∫σ(ϑ)sinϑdϑ , |
(1.17) |
|
4π |
0 |
|
которое в общем случае зависит от энергии E1 налетающей частицы. Здесь полное сечение σ(E1 ) отличается от дифференциального постоянным и
наперед заданным аргументом. Наглядное представление о полном сечения (1.17) в данном случае можно получить, если считать эту величину некоторым эффективным с точки зрения взаимодействия поперечным сечением частицымишени. Иными словами, только те налетающие точечные частицы, которые
попадают в это эффективное поперечное сечение, будут испытывать в результате взаимодействия отклонение от прямолинейной траектории движения на какой-либо угол ϑ . Такое простое представление полностью соответствует выражению (1.2), поскольку из него вытекает равенство
σ(E1 ) = |
σ ( E1 ) |
bmax |
(1.18) |
∫dσ = |
∫2πbdb . |
||
|
0 |
0 |
|
Полная площадь σ(E1 ) образуется, таким образом, из всех элементов площади в пределах некоторого максимального прицельного расстояния bmax , для
которых отличны от нуля углы рассеяния.
Полное число рассеянных и испытывающих отдачу частиц-мишеней не зависит от системы отсчета, поэтому полное сечение одно и то же как в лабораторной системе, так и в системе центра инерции, а также для обоих видов разлетающихся частиц несмотря на то, что все дифференциальные сечения рассеяния различны. В частности, используя выражения (1.6) и (1.11) получаем
σ(E1 ) = ∫σ(ϑ)dΩ = ∫σ(ϑ1 )dΩ1 |
= ∫σ(ϑ2 )dΩ2 , |
(1.19) |
|
4π |
4π |
4π |
|
а из выражения (1.14) следует, что полное сечение можно получить также интегрированием по всей области изменения энергии отдачи
σ(E1 ) = ∫σ(ϑ)dΩ = ∫σ(E2′; E1 )dE2′ . |
(1.20) |
4π |
|
Таким образом, величина σ(E1 ) и предельное расстояние bmax дают в данном
случае некоторую общую характеристику взаимной рассеивающей способности частиц для рассмотренного конкретного процесса.
Понятие о парциальном сечении рассеяния для рассматриваемого случая заданного вида взаимодействия можно ввести, если интегрирование по одной или нескольким переменным производить не по всей области их изменения. Пусть, например, частицами-мишенями являются атомы водорода в молекуле воды, а величина Ed представляет собой ту минимальную энергию,
передаваемую атому водорода, которая необходима для разрыва его химической связи с атомом кислорода и необратимого превращения в ион
водорода |
H + |
или в нейтральный высокореактивный химический радикал |
|
водорода |
H • . |
Понятно, что такой процесс сопровождается одновременным |
|
образованием |
гидроксильной группы OH − |
или радикала OH • . |
|
Высокоактивные химические радикалы играют важную роль в создании первичных повреждений в биологических объектах. В этом случае можно
ввести, например, парциальное (или неполное) сечение σ(Ed ; E1 ) |
передачи |
энергии E2′ ≥ Ed атому водорода |
|
σ(Ed ; E1 ) = ∫σ(E2′; E1 )dE2′ , |
(1.21) |
E2′ ≥Ed |
|
которое совпадает с полным сечением только приEd = 0 .
В данном случаевеличина σ(Ed ; E1 ) и энергия Ed дают некоторую общую
характеристику процесса образования свободных радикалов воды либо ионов H + и OH − за счет выбивания водорода из молекул воды. В этом смысле из парциального сечения σ(Ed ; E1 ) можно в свою очередь выделить парциальное
сечение образования радикалов и сечение образования ионов. Как будет описано ниже, вероятность образования ионов водорода велика только при передаче очень больших энергий, поскольку медленно движущиеся ионы водорода достаточно быстро восстановятся до состояния нейтрального атома водорода. Далее, если под Ed понимать энергию, которая необходима для
необратимого смещения атома из данного узла кристаллической решетки в твердом теле, то выражение (1.21) представляет собой парциальное сечение такого процесса смещения. Эта величина играет важную роль при описании облучения твердых тел и также будет рассматриваться ниже более детально. Описанную картину для полного и парциальных сечений легко обобщить на произвольные процессы рассеяния.
Везде выше полагалось, что сечение σ(E1 ) и максимальное прицельное расстояние bmax в соотношении (1.18) являются конечными величинами. В этом случае выражение
p(ϑ)dΩ =σ −1 (E )σ(ϑ)dΩ |
(1.22) |
1 |
|
представляет собой вероятность того, что частица из падающего однородного моноэнергетического параллельного пучка рассеется в элемент телесного угла dΩ около направления ϑ . Поэтому величина p(ϑ) , нормированная на единицу
σ −1 (E1 )4∫πσ(ϑ)dΩ =1,
представляет собой плотность вероятности рассеяния на угол ϑ . Однако не для всех видов взаимодействия величина σ(E1 ) является конечной и тогда
выражение (1.22) нельзя интерпретировать, строго говоря, как вероятность. Но и в этом случае отношение двух дифференциальных или парциальных сечений дает информацию о том, какое из двух событий более вероятно.
Как при классическом, так и при квантовом описании рассеяния полное сечение оказывается бесконечно большим для дальнодействующих потенциалов, которые медленно убывают с расстоянием r . Тогда для любого прицельного расстояния угол рассеяния ϑ оказывается отличным от нуля, все частицы испытывают большее или меньшее отклонение, а полное сечение в соответствии с (1.18) расходится. При квантовом описании рассеяния к бесконечному полному сечению приводят, например, все потенциалы,
которые убывают медленнее, чем 1 r2 . Всегда конечным полное сечение
r2 . Всегда конечным полное сечение
рассеяния будет, если имеется “обрезанный” потенциал, точно равный нулю за пределами некоторого расстояния. Один из таких простых, но важных
потенциалов – это потенциал “жесткой сферы”, приводящий к очень простому закону рассеяния. Кроме того, во многих практических расчетах нижний предел, как в формуле (1.21), обрезает расходимость. В некоторых других случаях расходящиеся дифференциальные сечения входят в подынтегральное выражение вместе с функциями, устраняющими особенность, что дает возможность получать важные и физически осмысленные результаты.
1.6 Макроскопические сечения рассеяния
Понятие о макроскопическом сечении рассеяния можно ввести на примере такой важной характеристики частицы, взаимодействующей с веществом, как средняя длина свободного пробега. Вещества, через которые проходят частицы из падающего пучка, и особенно биологические среды, состоят, как правило, из разных типов молекул и атомов, в результате чего частица может по разному рассеиваться на каждой из частиц-мишеней. Кроме того, столкновения могут быть разного типа – упругие, неупругие, с возбуждением или ионизацией и т.д. При заданных характеристиках падающей частицы (масса, заряд, начальная энергия и др.) характер взаимодействия, его величина и тип столкновения определяются, очевидно, видом частицы-мишени. Будем обозначать индексом i некоторый i -й тип из числа всех возможных взаимодействий и оценим среднюю длину свободного пробега с учетом взаимодействия всех типов.
Для определения длины свободного пробега, проходимого частицей между двумя последовательными столкновениями с частицами вещества, достаточно определить полное число столкновений, испытываемых частицей при прохождении некоторого микроскопического расстояния ∆R . Микроскопичность величины ∆R в дальнейших выкладках предполагает, что несмотря на множественность столкновений энергия частицы E1 не успевает
измениться существенно, так что столкновения происходят в приближенно равных условиях. Тогда число столкновений i -го типа пропорционально,
очевидно, числу частиц-мишеней в объеме V = ∆Rσi (E1 ) и равно ni ∆Rσi (E1 ) , где ni - плотность частиц-мишеней, участвующих в столкновениях i -го типа.
Полное число столкновений получаем суммированием по i , поэтому средняя длина свободного пробега приближенно равна
λ = ∆R[∑nσ |
(E )∆R]−1 |
=[∑nσ |
(E )]−1 |
≡[∑Σ |
(E )]−1 |
≡ (Σ)−1 . |
(1.23) |
|||
i |
i i |
1 |
i |
i i |
1 |
i |
i |
1 |
|
|
|
|
|
|
|
|
|
|
|||
Произведение niσi (E1 ) = Σi (E1 ) |
называется |
макроскопическим |
сечением |
|||||||
столкновений i -го типа, которое определяет длину свободного пробега между столкновениями этого типа: λi = Σi (E1 )−1 =[niσi (E1 )]−1 . Величину Σ(E1 ) можно
интерпретировать как полное макроскопическое сечение рассеяния, которое вместе с длиной свободного пробега зависит от текущего значения энергии налетающей частицы E1 .
Далее, если пучок взаимодействует с материалом мишени, то можно вычислить скорость, с которой протекает в мишени данная реакция. Реакцией может быть рассеяние налетающих частиц или какой-либо другой процесс, например, ионизация атомов мишени, образование высокоактивных химических радикалов и т.д.. Пусть i по-прежнему нумерует интересующий нас процесс в ряду других возможных процессов, тогда через σi (E1 ) запишем
присущее этому процессу сечение, а через n2 – пространственную плотность
частиц-мишеней вещества, участвующих в реакции. В этом случае для независящего от времени потокачастицскоростьреакцииописывается выражением
dnr = n σ |
(E )Φ = Σ |
Φ, |
(1.24) |
|||
dt |
2 |
i |
1 |
i |
|
|
|
|
|
|
|
|
|
где nr - пространственная плотность процессов реакции. По существу это уравнение
означает, что пространственная плотность процессов взаимодействия зависит от энергетических характеристик налетающих частиц только через полное сечение
процесса |
σi (E1 ) |
или макроскопическое сечение Σi (E1 ) . В частном |
случае |
|
образования высокоактивных химических радикалов воды или ионов H + |
и OH − |
|||
при выбивании |
атомов или ионов водорода из молекул воды |
сечение |
||
σi (E1 ) =σ(Ed ; E1 ) , |
величина n2 есть концентрация атомов водорода |
воды, а |
||
величина |
nr |
представляет собой пространственную плотность образующихся |
||
радикалов H • |
и/или ионов H + . Заметим, что последние в радиационной физике |
|||
принято называть протонами отдачи точно так же, как выбитые атомы называют атомами отдачи.
В определении (1.24) снова подразумевается, что энергия частицы E1 с
учетом всех видов взаимодействия практически не изменяется при прохождении через вещество, так что макроскопическое сечение остается постоянным, как и плотность потока. Идеальным является, очевидно, случай, когда материал мишени настолько тонкий, что позволяет исключить перекрытие (“маскирование”) сечений реакции и помешать налетающей частице дважды участвовать в реакции с материалом мишени. Например, в процессе упругих столкновений нейтронов с атомами решетки кристалла, для которых полное сечение σ ≈10−24 см2, формула (1.24) справедлива, строго говоря, для мишеней с толщиной порядка 1см. При торможении тяжелых ионов в твердых телах справедливость выражения (1.24) ограничивается гораздо меньшей толщиной. Наоборот, для биологических объектов, имеющих существенно меньшую плотность, чем у твердых тел, толщина мишени может быть больше. Однако в любом случае необходимо учитывать изменение параметров (энергии и плотности потока) налетающих частиц по мере их прохождения через вещество. Поэтому применять соотношения типа (1.24) следует для тонких слоев с учетом изменения в процессе прохождения через вещество энергии и пространственной конфигурации пучка частиц.
При рассмотрении радиационно стимулированной реакции в тонком слое выражение (1.24) можно трансформировать так, чтобы выразить поглощенную дозу излучения через пространственную плотность процессов реакции. По определению доза излучения D есть полная энергия, переданная излучением единице массы вещества. Для относительно тонкого слоя под дозой следует понимать энергию, переданную единице массы слоя. Если поток частиц через слой не изменяется со временем, а изменение плотности частиц-мишеней n2 пренебрежимо мало, то уравнение (1.24) после
интегрирования по времени можно записать в виде
Di = nr E2′ i ρ−1 = n2σi (E1 ) E2′ i Φρ−1 , |
(1.25) |
где ρ - удельная плотность вещества. Здесь Di есть доза излучения, обусловленная i -й реакцией, а величина  E2′
E2′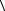 i представляет собой среднюю передаваемую в процессе этой реакции энергию. В частности, если речь идет
i представляет собой среднюю передаваемую в процессе этой реакции энергию. В частности, если речь идет
об образовании радикалов воды или ионов H + |
|
и OH − , |
то средняя энергия, |
|||
передаваемая протону отдачи, описывается выражением |
(1.26) |
|||||
E2 i =σ |
|
(Ed ; E1 ) |
∫ E2σ(E2 |
; E1 )dE2 . |
||
′ |
−1 |
|
′ |
′ |
′ |
|
|
|
|
E2′ ≥Ed |
|
|
|
Подставляя выражение (1.26) в (1.25) и учитывая равенство σi (E1 ) =σ(Ed ; E1 ) , получаем выражение
Di = nr |
E2 |
i |
ρ |
|
= Φρ |
|
n2 |
∫ E2σ(E2 |
; E1 )dE2 . |
(1.27) |
|
′ |
|
|
−1 |
|
−1 |
|
′ ′ |
′ |
|
|
|
|
|
|
|
|
|
E2′ ≥Ed |
|
|
Выражение (1.27) дает явную зависимость дозы излучения, поглощенной при протекании данной реакции образования ионов и радикалов воды, от выхода реакции и связь дозы излучения с параметрами пучка налетающих частиц и дифференциальным сечениемпередачи энергии дляданнойреакции.
Если учитывать все радиационно стимулированные процессы, приводящие к данной реакции, то величину Σi в уравнении (1.24) следует
заменить, очевидно, на полное макроскопическое сечение Σ, которое является суммой сечений этих процессов. В частности, в процессе торможения кинетическая энергия заряженных частиц может идти на возбуждение и
ионизацию атомов среды. Поэтому свободные радикалы воды OH • могут появляться, например, в результате цепочки химических реакций после ионизации молекулы воды
H2O → H2O•+ + e− , H2O•+ + H2O → OH • + H3O+
или путем выбивания лишнего спаренного электрона из гидроксильной группы
OH −
OH − → OH • + e− .
Отметим, что ионизационное или электронное торможение является главным

механизмом потерь энергии при прохождении любой заряженной частицы через вещество. Электроны, выбитые из атомов в процессе ионизации,
называются δ -электронами или вторичными электронами. Понятно, что при достаточно большой энергии вторичные электроны могут в свою очередь приводить к появлению радикалов H • и ионов H + в результате взаимодействия с ядрами атомов водорода в молекулах воды.
С учетом такого независимого канала реакции образования радикалов и ионов под действием вторичных электронов вместо уравнения (1.24) следует записать уравнение
d(nH ,i + nH ,e ) |
= n |
[σ |
(E )Φ +σ |
|
(E |
|
)Φ |
] = Σ |
Φ + Σ |
Φ |
|
, |
(1.28) |
|
e |
e,1 |
e |
||||||||||
dt |
2 |
i |
1 |
|
e |
i |
e |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
где Φe есть некоторая эффективная плотность потока вторичных электронов, энергии которых Ee,1 достаточно для образования радикалов. Нетрудно видеть,
что уравнение (1.28) получается путем простого сложения двух уравнений, каждое из которых соответствует своему каналу реакции образования радикалов или ионов с пространственной плотностью nH ,i и nH ,e . В
соответствии с этим полная доза излучения, поглощаемая при образовании радикалов или ионов воды, имеет вид суммы
Di + De = nH ,i E2′ |
i ρ−1 + nH ,e |
|
E2′ e ρ−1 |
= |
|
|
|
|
(1.29) |
|||
= Φρ |
−1 |
n2 |
′ |
′ |
′ |
+Φe ρ |
−1 |
n2 |
′ |
′ |
′ |
|
|
∫ E2σi (E2 |
; E1 )dE2 |
|
∫ E2σe (E2 |
; Ee,1 )dE2 . |
|||||||
|
|
|
|
E2′ ≥Ed |
|
|
|
|
|
E2′ ≥Ed |
|
|
Важно подчеркнуть, что сумма Di + De не равна в действительности полной дозе
излучения D , поскольку не включает в себя те потери энергии налетающих частиц, которые не приводят к появлению указанных структурных дефектов при взаимодействии с веществом. И наоборот, сумма (1.29) не описывает в действительности дозу излучения во всех возможных каналах реакции, связанных с образованием ионов и радикалов воды. Они могут образовываться, например, под действием уже выбитых из молекул воды быстрых ионов водорода или других вторичных выбитых ионов.
Отметим, наконец, что доза излучения Di + De выражается через число
возникающих структурных дефектов, а не наоборот. Иными словами, в соответствии с (1.27) и (1.29) каждый акт появления структурного дефекта сопровождается потерей энергии налетающей частицы, однако само число возникающих дефектов в каждом канале реакции определяется согласно (1.24) и (1.28) макроскопическим сечением этой реакции и флюенсом налетающих частиц. Макроскопическое сечение зависит только от полного сечения процесса, минимально необходимой для образования дефекта энергии (нижний предел в интегралах типа (1.21)) и плотности атомов в веществе. Аналогичным образом, эффективный флюенс вторичных высокоэнергетичных электронов также определяется только полным сечением процесса их образования при заданной энергии первичных падающих частиц (с
учетом соответствующего порогового значения энергии образования вторичного электрона)и флюенсом налетающихчастиц.
Задачи
Задача 1.1. Получить явную зависимость угла рассеяния ϑ от угла рассеяния ϑ1 при m1 > m2 .
Задача 1.2. Используя явную зависимость угла рассеяния ϑ от угла рассеяния ϑ1 , получить дифференциальное сечение рассеяния налетающих
частиц σ(ϑ1 ) в лабораторной системе отсчета при m1 ≤ m2 .
Задача 1.3. Получить дифференциальное сечение рассеяния налетающих частиц σ(ϑ1 ) в лабораторной системе отсчета при m1 > m2 .
Задача 1.4. Используя явную зависимость угла рассеяния ϑ от угла рассеяния ϑ2 , получить дифференциальное сечение отдачи σ(ϑ2 ) в
лабораторной системе отсчета.
