
Формулы(гр. алфавит)
.DOC
Греческий алфавит
![]() альфа
alpha
альфа
alpha
![]() бета
beta
бета
beta
![]() гамма
gamma
гамма
gamma
![]() дельта
delta
дельта
delta
![]() эпсилон
epsilon
эпсилон
epsilon
![]() дзета
zeta
дзета
zeta
![]() эта
eta
эта
eta
![]() (или
(или
![]() )
тета theta
)
тета theta
![]() йота
iota
йота
iota
![]() каппа
kappa
каппа
kappa
![]() ламбда
lambda
ламбда
lambda
![]() мю
mu
мю
mu
![]() ню
nu
ню
nu
![]() кси
xi
кси
xi
![]() омикрон
omicron
омикрон
omicron
![]() пи
pi
пи
pi
![]() ро
rho
ро
rho
![]() сигма
sigma
сигма
sigma
![]() тау
tau
тау
tau
![]() ипсилон
upsilon
ипсилон
upsilon
![]() (или
(или
![]() )
фи phi
)
фи phi
![]() хи
chi
хи
chi
![]() пси
psi
пси
psi
![]() омега
omega
омега
omega
Эквивалентные функции
при
![]()
-
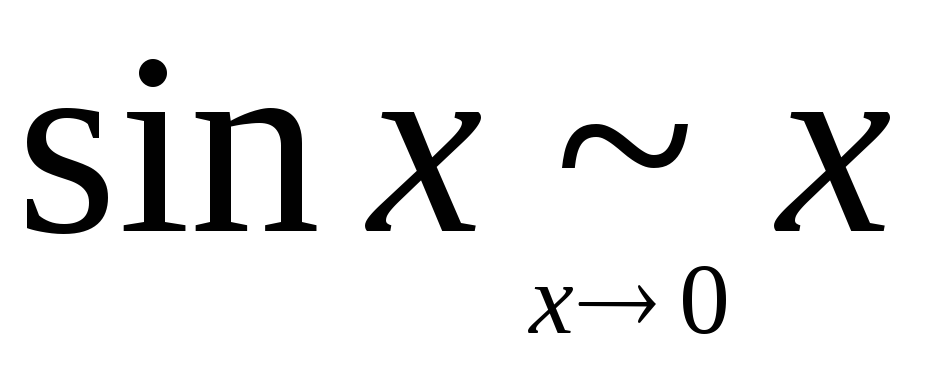 .
. -
 .
. -
 .
. -
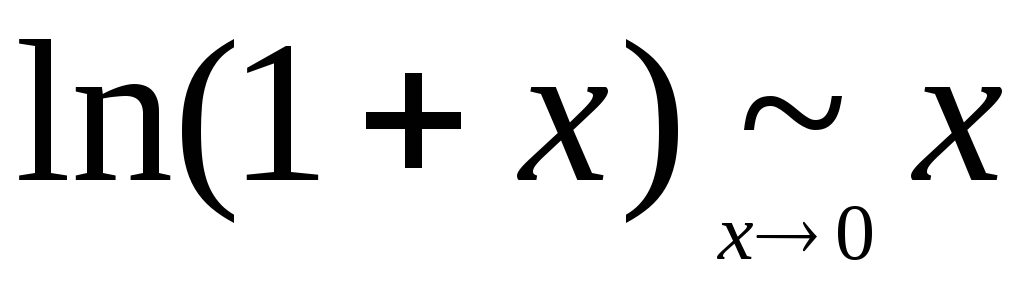 .
. -
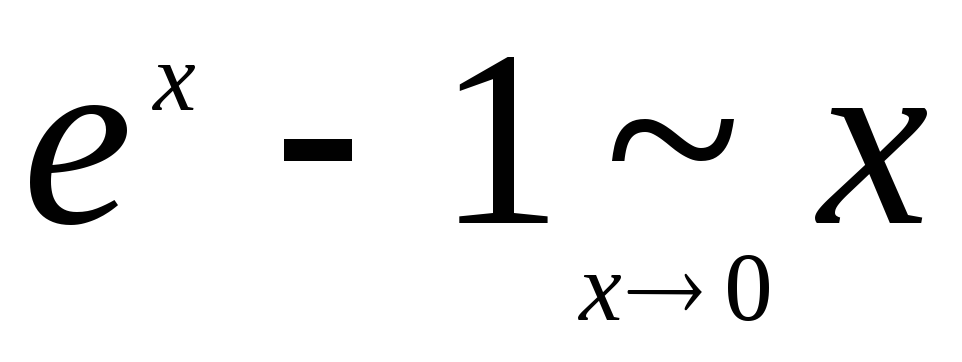 .
. -
 ,
,
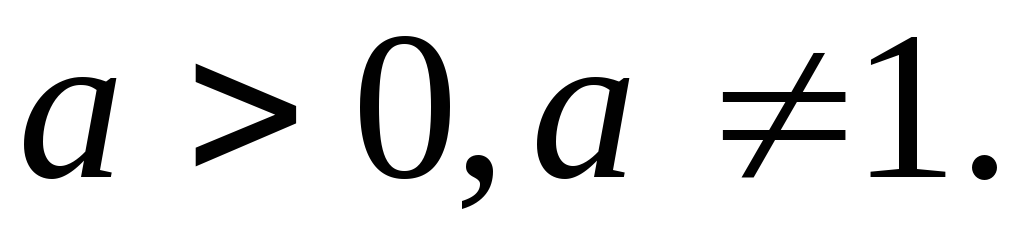
-
 ,
,
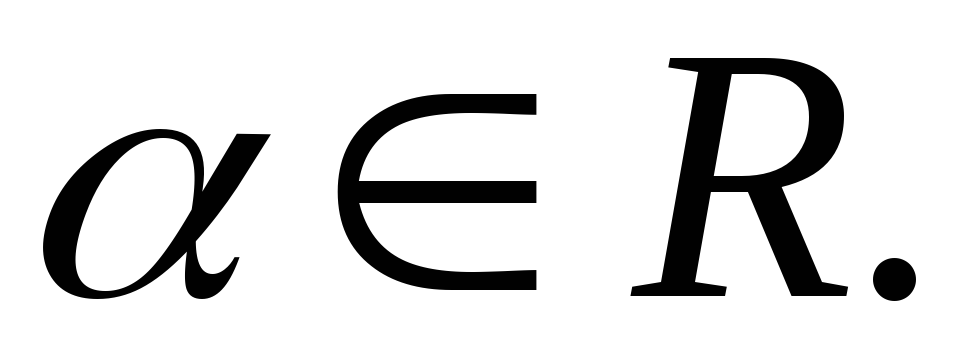
-
 .
. -
 .
.
10.
![]()
![]() где
где
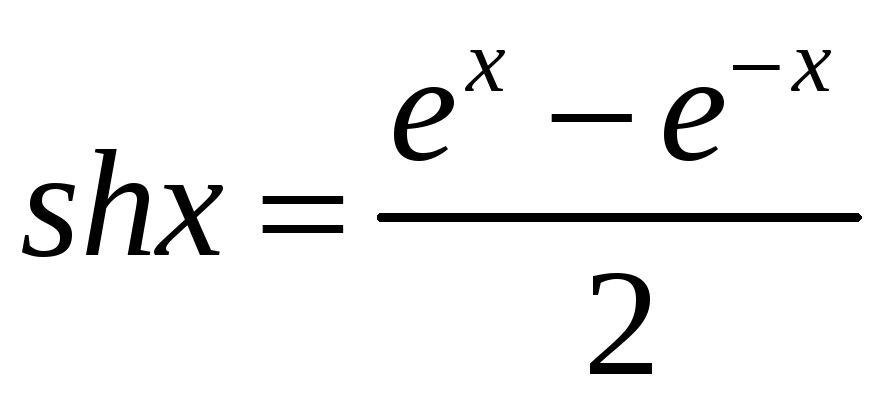 .
.
11.
![]()
![]() где
где
![]()
12.
![]() .
.
Сравнение функций. O(f) и o(f).
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
![]()
10.
![]() .
.
11.
![]() .
.
12.
![]() .
.
12.
![]() .
.
13.
![]() .
.
14.
![]() .
.
15.![]() .
.
16.

Таблица производных
-
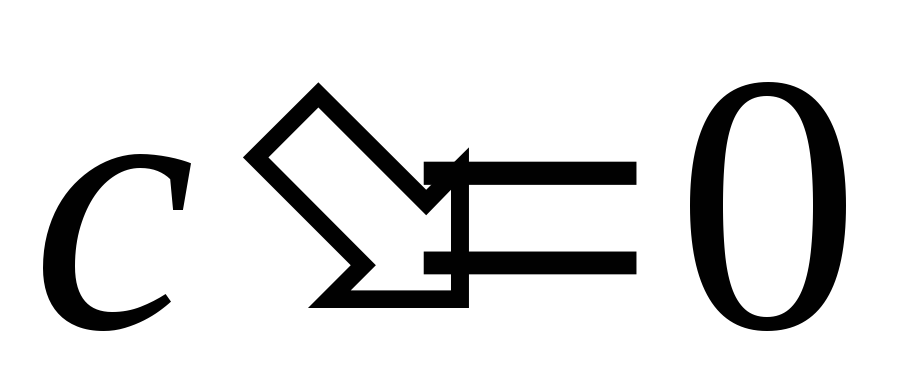 ,
,
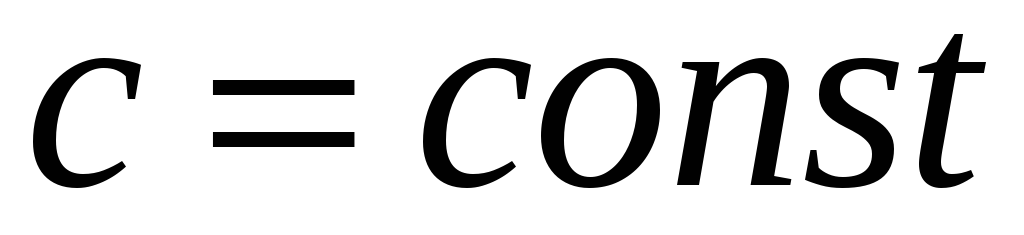
-



![]()
![]()
![]()
3.
![]()
![]()
![]()
![]()
![]()
4.
![]()
![]()
![]()
![]()
![]()
5.
![]()
![]()
6.
![]()
![]() 7.
7.
![]()
![]()
![]()
8.
![]()
![]()
![]()
9.
![]()
![]()
10.
![]()
![]()
11.
![]()
![]()
12.
![]()
![]()
13.
![]()
![]() где
где
![]()
14.
![]()
![]() где
где
![]()
15.
![]()
![]()
![]()
16.
![]()
![]()
Производные высших порядков
1)
![]() ,
,
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ,
,
![]() .
.
Если
функции
![]() и
и
![]() имеют производные
порядка
имеют производные
порядка
![]() ,
то функции
,
то функции
![]() (
(![]() -постоянные)
и
-постоянные)
и
![]() также имеют производные порядка
также имеют производные порядка
![]() ,
причем
,
причем
6)
![]() ;
;
7)
![]() - формула
Лейбница.
- формула
Лейбница.
Формулы Маклорена для основных элементарных функций
![]()
1.
![]()
2.
![]()
3.
![]()
4.
![]() где
где
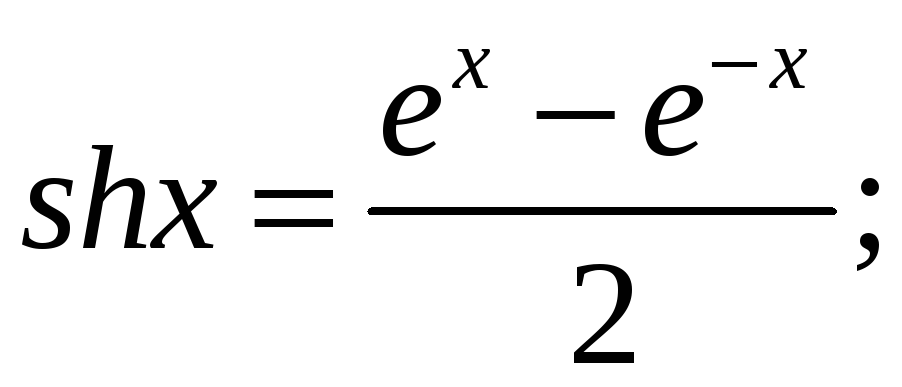
5.
![]() где
где

6.
![]()
6.1.
![]()
![]()
7.
![]()
7.1.
![]()
8.
![]()
9.
![]()
10.
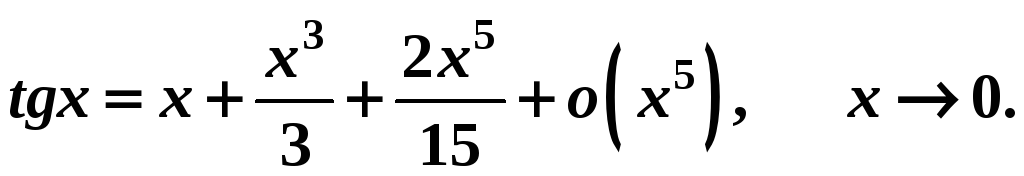
Если![]() - четная функция, то:
- четная функция, то:
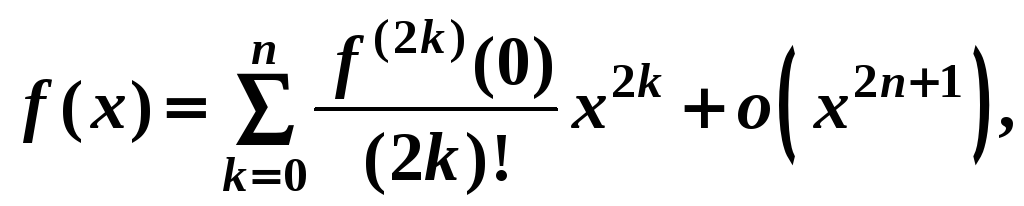
если![]() - нечетная функция, то:
- нечетная функция, то:

Исследование функций и построение графиков
-
Найти область определения функции.
-
Исследовать, не является ли функция четной или нечетной.
-
Исследовать, не является ли функция периодической.
-
Исследовать поведение функции в окрестности точек разрыва. Выписать вертикальные асимптоты.
-
Найти точки пересечения с осями координат и промежутки постоянства знака.
-
Найти горизонтальные и наклонные асимптоты.
-
Определить промежутки убывания и возрастания функции, а также точки экстремума.
-
Найти точки перегиба и установить промежутки выпуклости вверх и вниз графика функции.
-
Построить график функции.

Исследование функций и построение графиков
-
Найти область определения функции.
-
Исследовать, не является ли функция четной или нечетной.
-
Исследовать, не является ли функция периодической.
-
Исследовать поведение функции в окрестности точек разрыва. Выписать вертикальные асимптоты.
-
Найти точки пересечения с осями координат и промежутки постоянства знака.
-
Найти горизонтальные и наклонные асимптоты.
-
Определить промежутки убывания и возрастания функции, а также точки экстремума.
-
Найти точки перегиба и установить промежутки выпуклости вверх и вниз графика функции.
-
Построить график функции.
Таблица неопределенных интегралов
1.
![]() 2.
2.
![]()
3.
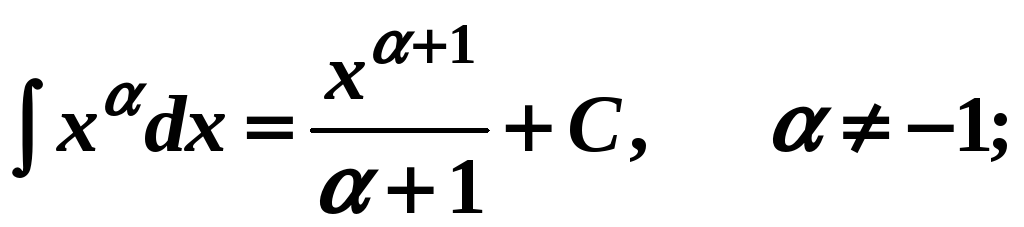
4.
![]()
5.
![]()
6.
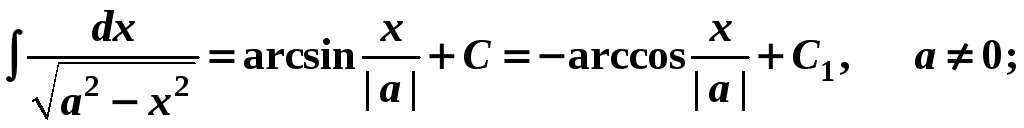
7.

![]()
8.
![]() 9.
9.
![]()
10.
![]()
11.
![]()
12.
![]() где
где
13.
![]() где
где

14.
![]()
15.
![]()
16.
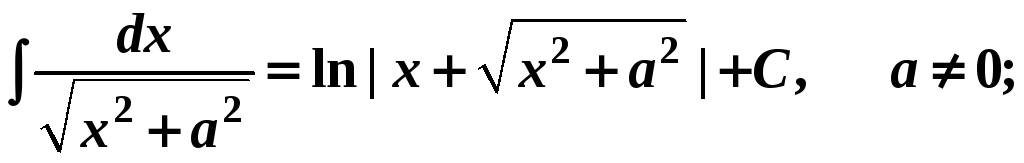
17.
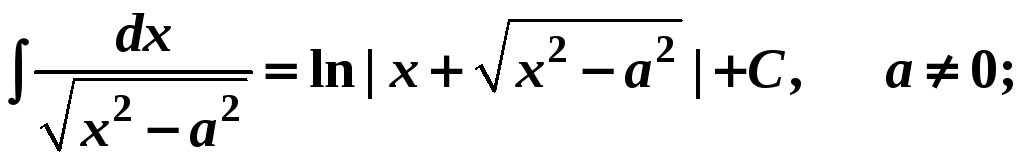
18.

19.
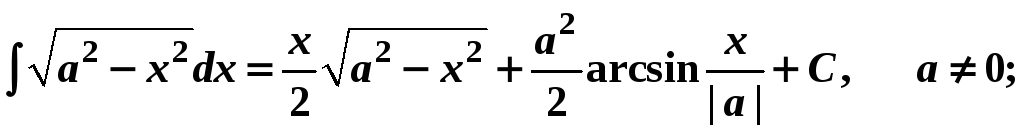
20.
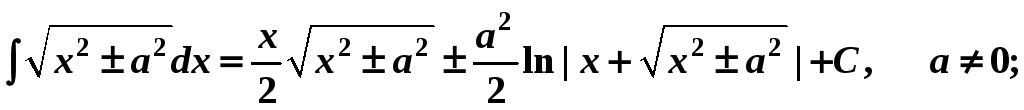
21.
![]()
22.
![]()
Интегралы, сводящиеся к интегралам от рациональных функций
Всюду в
указанных формулах через
![]() обозначается некоторая рациональная
функция от переменных
обозначается некоторая рациональная
функция от переменных
![]() и
и
![]() ,т.е.
,т.е.
![]() ,
где
,
где
![]() -
многочлены степеней
-
многочлены степеней
![]() и
и
![]() соответственно от переменных
соответственно от переменных
![]() и
и
![]() .
.
-
Интегралы вида
![]() ,
,
![]() .
(1)
.
(1)
Положим
![]() .
Тогда
.
Тогда
![]() .
.
В силу формулы замены переменных в неопределённом интеграле
![]() =
=![]() .
.
Т.о. вычисление
интеграла вида (1) сводится к вычислению
интеграла от рациональной функции
переменной
![]() .
.
-
Интегралы вида
![]() ,
,
![]() .
(2)
.
(2)
Выражение, стоящее под знаком интеграла, называется биномиальным дифференциалом.
П.Л. Чебышев доказал, что интегралы этого вида выражаются через элементарные функции лишь в трёх случаях:
1)
![]() .
.
Пусть
![]() где
где
![]() .
.
Положим
![]() где
где
![]() -
наименьшее общее кратное чисел
-
наименьшее общее кратное чисел
![]() и
и
![]() .
Данная замена переменной сводит
вычисление интеграла (2) к вычислению
интеграла от рациональной функции
переменной
.
Данная замена переменной сводит
вычисление интеграла (2) к вычислению
интеграла от рациональной функции
переменной
![]() .
.
2)
![]() .
.
Пусть
![]() где
где
![]() .
.
Положим
![]() .
Данная замена переменной приводит к
вычислению интеграла от рациональной
функции переменной
.
Данная замена переменной приводит к
вычислению интеграла от рациональной
функции переменной
![]() .
.
3)
![]() .
.
Пусть
![]() где
где
![]() .
Положим
.
Положим
![]() .
Данная замена переменной приводит к
вычислению интеграла от рациональной
функции переменной
.
Данная замена переменной приводит к
вычислению интеграла от рациональной
функции переменной
![]() .
.
-
Интегралы вида
![]() ,
,
![]() .
(3)
.
(3)
Для рационализации интегралов этого вида применяются подстановки Эйлера трех типов.
1)
Если
![]() ,
то полагаем
,
то полагаем
![]() или
или
![]() .
.
2)
Если
![]() ,
то полагаем
,
то полагаем
![]() или
или
![]() .
.
3)
Если квадратный трехчлен
![]() имеет различные вещественные корни
имеет различные вещественные корни
![]() и
и
![]() ,
то полагаем
,
то полагаем
![]() или
или
![]() .
.
Подстановки Эйлера универсальны (т.е. применимы к любому интегралу указанного вида). Однако во многих случаях они приводят к неоправданно сложным рациональным функциям. Поэтому часто используют другие методы, основанные на элементарных преобразованиях.
Еще одна полезная формула, применимая к интегралам вида
![]() ,
где
,
где
![]() полином
полином
![]() -й
степени,
-й
степени,
![]() :
:
![]() .
.
В этой формуле
![]() многочлен
многочлен
![]() - й степени с неизвестными коэффициентами,
- й степени с неизвестными коэффициентами,
![]() -
неизвестный множитель. Для отыскания
этих неизвестных величин указанное
равенство дифференцируют, а результат
после умножения на
-
неизвестный множитель. Для отыскания
этих неизвестных величин указанное
равенство дифференцируют, а результат
после умножения на
![]() и приравнивания коэффициентов при
соответствующих степенях
и приравнивания коэффициентов при
соответствующих степенях
![]() дает систему уравнений для отыскания
коэффициентов многочлена
дает систему уравнений для отыскания
коэффициентов многочлена
![]() и множителя
и множителя
![]() .
.
-
Интегралы вида
![]() (4)
(4)
всегда рационализируются универсальной подстановкой
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
,
![]() .
.
Специальные случаи:
1)
Если
![]() ,
то полагаем
,
то полагаем
![]() .
.
2)
Если
![]() ,
то полагаем
,
то полагаем
![]() .
.
3)
Если
![]() ,
то полагаем
,
то полагаем
![]() или
или
![]() .
.
Иногда удобно преобразовывать подинтегральную функцию, имеющую вид произведения синусов и косинусов (или их степеней), в сумму, пользуясь формулами понижения степени или другими тригонометрическими формулами.
-
Интегралы вида
![]() ,
,
![]() (5)
(5)
рационализируются
при помощи подстановки
![]() ,
где
,
где
![]() -
наименьшее общее кратное знаменателей
чисел
-
наименьшее общее кратное знаменателей
чисел
![]() .
.
Выражения типа
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() интегрируются
по частям.
интегрируются
по частям.
Интегралы, не берущиеся в конечном виде. Существует много выражений, которые имеют первообразные, однако, эти первообразные не могут быть представлены в виде “формулы”, т.е. комбинации конечного числа элементарных функций. В этом случае говорят, что интеграл не берется в конечном виде. Среди основных таких интегралов необходимо помнить следующие:
1.
![]() (“интегральный логарифм”);
(“интегральный логарифм”);
2.
![]() (“интегральный синус”);
(“интегральный синус”);
3.
![]() (“интегральный косинус”);
(“интегральный косинус”);
4.
![]() и
т.д.
и
т.д.
Не берутся в конечном виде также интегралы, приводящиеся к этим.
Ряды Тейлора для основных элементарных функций
Аналитическая
в точке
![]() функцию
функцию
![]() может быть представлена степенным
рядом
может быть представлена степенным
рядом
 ,
,
![]() .
.
