2.Традиционное деление суждений

Суждения можно различать с т.зр. 1) количества, 2) качества, 3) отношениями 4) модальности.

Количество суждения

Если субъект в суждении взят в полном объеме, суждение называется общим;

Если субъект взят в части объема, суждение наз. частным.

Формула общего суждения: Все S суть P

Формула частного суждения: Некоторые S суть P

От частных суждений нужно отличать еди­ничные, или индивидуальные, суждения (субъект – индивидуальное или единичное понятие). Индивидуальные суждения относят к общим суждениям, так как в них предикат относится к субъ­екту, взятому во всём объёме.

Качество суждения

С точки зрения качества суждения де­лятся на утвердительные и отрицательные.

Предикат придаём субъекту – утвер­дительное суждение. S есть Р.

Предикат у субъ­екта исключаем (изымаем) – суждение будет отрицательное. S не есть Р.

Соединим признаки количества и качества. Получим обще-утвердительные и частно-утвердительные, обще-отрицательные и частно-отрицательные суждения.

Формулы этих суждений будут следующие:

А: Все S суть Р.

I : Некоторые S суть Р.

Е: Ни одно S не есть Р.

О: Некоторые S не суть Р.

По отношению: Категорические, условные и разделительные

Категорические суждения

Субъект утверждается или отри­цается относительно предиката без условий или ограничений (местом, временем, обстоятельствами). Схема категорического суждения: S есть Р.

Условные, или гипотетические, суждения

Когда отношение S и P ограничено каким-либо условием, то суждение называется условным. Схема условных суждений: Если А есть В, тo С есть D.

В условных суждениях, таким образом, мы имеем два суждения, которые находятся друг к другу в от­ношении основания предыдущий (antecedens) к следствию последую­щий (consequens). Оно сложное.

Разделительные суждения

Когда в суждении оставляется место неопределенности, оно называется разделительным. Разделительные суждения имеют, двоякий вид:

1) S есть или а, или в, или с.

2) Или а, или в, или с есть р.

Условно-разделительные суждения

Из соединения условных суждений с разделительными образуются условно- разделительные суждения.

Их схема:

Если А есть В, то С есть или D, или Е, или F,

Если есть A, то есть или а, или b, или с.

Модальность суждений

С этой точки зрения рассматривается, с какой квалифи­кацией, т. е. каким образом (cum modo), в суждении сказуемое приписывается подлежащему.

1. Проблематические — «S, вероятно, есть Р».

2. Ассерторические — «S есть Р».

3. Аподиктические — «S необходимо должно быть Р».

Три признака — возможность, действительность, необхо­димость

ОБЪЁМЫ ПОДЛЕЖАЩЕГО И СКАЗУЕМОГО в категорических суждениях

В аристотелевской логике (силлогистике – первом в истории исчислении имен), рассматриваются четыре вида категорических суждений: SaP, SeP, SiP, SoP. Это т.н. атомарные высказывания в силлогистике.

Вопрос об отношениях между S и P в этих суждениях сводится к вопросу: как относятся S и P по объему.

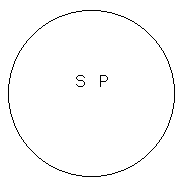
Суждения А. (все S суть Р).

Пример: «все рыбы суть позвоночные» Т.е. субъект есть подчиненное предикату понятие.

Но иногда в обще-утвердительных суждениях подлежащее и ска­зуемое будут понятиями равнозначащими. Пример: «все квадраты суть параллелограммы с равными сторонами и равными углами».

Суждения Е. В этом суждении мыотрицаемвсякое совпадение между подлежащим и сказуемым; один класс находится вне другого класса. Мы в мышлении совершенно от­деляем класс подлежащего от класса сказуемого.Пример: «ни одно насекомое не есть позвоночное».

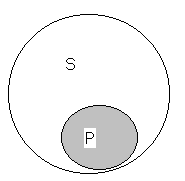
Суждения I. В этом суждениичастькласса «Sвходит в объём классаР,т. е. совпадает с классомР, т. е. круги должны пересекаться. Та часть S, о которой утверждается в Р, на рисунке заштрихована. В этом виде суждений субъект и предикат есть понятия пересекающиеся.

Пример: «неко­торые книги полезны».

Та часть объема, о которой говорится в суждении, является результатом умноженияпонятийSиP.

Может быть так, что весь целиком объем S (а не часть его) входит в объем Р. Пример: «некоторые животные суть позвоночные».

В этом случае SiP суждений оказывается, что предикат подчинен субъекту (а не наоборот, как это было в случае SaP).

Та часть объема, о которой говорится в суждении, является результатом умноженияпонятийSиP.

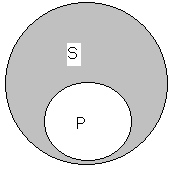
Суждения О. Пример: «неко­торые книги не суть полезны». Это суждение означает, что некоторая часть S не входит в объём Р.

Разница между SiPиSoPта, что вI мы обращаем внима­ние на то,что есть совпадающего между S и Р, авО— на то,что есть не совпадающего между S и Р.

Легко видеть, что часть объема, о которой говорится в суждении является результатом вычитанияPизS: (S–P).

SoP может быть таким, что S не пересекается с Р, а подчинен ему. Пример, суждение «некоторые змеи не имеют ядо­витых зубов».

Легко видеть, что здесь, также, часть объема, о которой говорится в суждении, является результатом вычитания P из S: (S – P).

Объёмы подлежащего и сказуемого.

Если подлежащее и сказуемое берутся в суждениях во всём объёме, то говорят, что они распределены;если они взяты не во всём объёме, то говорят, что онине распреде­лены.

На рис. распределённость подлежащего и сказуемого обозначается при помощи более широких линий:

S P

A распределено не распределено

E распределено распределено

I не распределено не распределено

O не распределено распределено

ПРОТИВОПОЛОЖНОСТЬ СУЖДЕНИЙ

Постановка вопроса.

Вообще, суждения, в которых один и тот же S и P, но которые имеют разные качества или количества или и то и другое, будут противоположными друг другу.

Вопрос состоит в том, насколько различные противоположные суждения логически совместимы (совозможны). В зависимости от этого между категорическими суждениями имеет место то или иное отношение противополжности.

Отношение 1. Противоречащие (контрадикторные) суждения отличаются и по количеству, и по качеству.

Отношение 2. Противные (контрарные) суждения отличаются только по качеству.

Отношение 3. Подчиненные суждения отличаются только по количеству.

Отношение 4 . Подпротивные (субконтрарные) суждения – это частные суждения, которые отличающиеся по качеству

Логическая совместимость есть возможность (или невозможность) противоположных суждений быть одновременно истинными (ложными.)

Противоречие (А — О, Е — I).

Из противоречащих суждений одно должно быть ис­тинным, а другое — ложным.

Два противоречащих суждения не могут быть в одно и то же время оба истинными, но не могут быть и оба ложными.

Противность (А — Е).

В двух противных суждениях из истинности одного следует ложность другого, но из ложности одного не следует истинность другого;

Оба суждения не могут быть истинными (потому что если одно истинно, то другое ложно), но оба могут быть ложн­ыми (потому что при ложности одного ложным может быть другое).

Подчинение (А—I, Е—О).

Общее истинно – частное непременно истинно, но не наоборот! При ложном общем суждении формально допустимо как ложное, так и истинное ччастное суждение

Частное ложно – тогда общее непременно ложно, но не наоборот! При истинном частном формально допустимо как истинное, так и ложное общее суждение.

Подпротивная противоположность (I—О).

Оба подпротивных суждения могут быть в одно и то же время истинными, но оба не могут быть ложными (по­тому что при ложности одного суждения другое является истинным).

A истинно,	E ложно,	O ложно,	I истинно
E истинно	A ложно	I ложно	O истинно
I истинно	A неопределенно	O неопределенно	E ложно
O истинно	E неопределенно	I неопределенно	A ложно
A ложно,	E неопределенно	I неопределенно	O истинно

Умозаключеие

Имеет место, когда из данных суждений формально (аподиктически) выводится новое суждение. Выведение нового суждения – есть отличительная черта формы умозаключения!!!

Рraemissae – посылки;

Типы размышления (логики)

1) индукция, 2) дедукция, 3) аналогия и т. п

НЕПОСРЕДСТВЕННЫе УМОЗАКЛЮЧЕНИЯ

Если умозаключения строятся на одной посылке это умозаключения в несобственном смысле, или умозаключения непосредственные.

Непосредственные умоза­ключения делятся на группы:

I. Умозаключения о противоположности, делятся на пять групп:

1. От подчиняющего к подчи­нённому (ad subordinatam).

2. От подчинённого к подчиняющему (ad subordinantem).

3. Ad соntradiсtоriam (А — О, Е — I).

4. Аd соntrаriam (А — Е).

5. Ad subcontrariam (I—О).

II. Превращение (obversio)

В процессе превращения меняется качество исходного суждения (утв. – отр.). Смысл исходного суждения не должен измениться!

Таким образом, всегда превращается: А – Е, Е – А, I – О, О – I. При этом Р обязательно меняется на не-Р.

Формально: S –на место S, не-Р – на место P + меняем качество суждения

A все S суть P…………………… E ни одно S не есть не-P

E ни одно S не суть P……… A все S суть не-P

I некоторые S суть P………… O некоторые S не суть не-P

O некоторые S не суть P …… I некоторые S суть не-P

III. Обращение (conversio)

В процессе превращения S меняется местами с P.

Формально: S –на место Р, P – на место S и не меняем качество суждения.

Обращение А:

Такое обращение, когда суждение изменяет своё коли­чество, называется: обращением посредством ограничения (con­versio per limitationem или per accidens). А обращается в I.

Когда S и P суждения А – понятия равнозначащие, обращение происходит чисто (conversio simplex).

Обращается: I – I, Е –Е,

Обращение SоP.

SоP вообще не обращаемо, поскольку в обращённом суждении должно получиться отрицательное суждение, следовательно, S нём должно быть распределено, между тем в обращаемом суждении оно как подлежащее частного суждения не распределено.

IV. Противопоставление (contraversio)

IV /1. Противопоставление субъекту

В этом случае предикат вывода становится не-S, субъект становится Р.

Формально:P – на место S; не-S – на место Р + изменяем качество исходного суждения.

Технически: последовательно производим обращение исходного суждения, затем результат обращения – превращаем.

A: Все S суть P……………….. Некоторые P не суть не-S

E: Ни одно S не есть P…… Все P суть не-S

I : Некоторые S суть P ….. Некоторые P суть не-S

O : Некоторые S не суть P – не противопоставляется S

IV /2. Противопоставление предикату

В этом случае субъект вывода становится не-P, предикат становится S.

Формально: S – на место P,– на место S + изменяем качество суждения.

Технически: производим превращение исходного суждения, затем результат – обращаем.

Возьмём противопоставление суждения О: «Некоторые несправедливые законы не отменены». Это суждение превращается в I: «Некоторые несправедливые законы суть не-отменённые законы»; а это суждение при обращении даёт: «некоторые не отмененные законы суть несправедливы». Суждение I, очевидно, не допускает противопоставления.

A: все S суть P………………..ни одно не-P не есть S

E: ни одно S не есть P………некоторые не-P суть S

O: некоторые S не суть P…...некоторые не-P суть S

I: некоторые S суть P – не допускает противопоставления.

ДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ. СИЛЛОГИЗМ

Определение силлогизма

Дедуктивные «умозаключения принимают формы силлогизма. Силлогизм есть такая форма умозаключения, в которой из двух суждений необходимо выте­кает третье, причём одно из двух данных суждений является общим. Силлогизм, та­ким образом, представляет собой умозаключение от общего. Полученное суждение ни в коем случае не будет более общим, чем суждения, из которых оно выводится.

Например, нам даются два суждения:

Все студенты разумные существа.

Эти существа – студенты.

Из них следует, что: Эти существа – разумны.

Части силлогизма.

Данные суждения называются предпосыл­ками или посылками (praemissae), а новое суждение, которое получается из сопоставления посылок, называется заключением (conclusio). Те понятия, которые входят в заключение и предпо­сылки, называются терминами (termini).

Подлежащее заключения называется меньшим термином (terminus minor).

Сказуемое заключения называется большим тер­мином (terminus major).

Термин, который не входит в заключение, называется средним термином (terminus medius).

S обозначает мень­ший термин, М — средний, Р — больший (см.рис.).

Средний термин называется средним потому, что он служит посредствующим связующим элементом между боль­шим и меньшим терминами. Средний термин служит для срав­нения большего термина с меньшим. Сами по себе эти термины не могут быть сравниваемы. Сравнение может происходить че­рез посредство среднего термина.

Суждение, в которое входит больший термин, называется большей посылкой; суждение, в которое входит меньший термин, называется меньшей посылкой.

Форма и содержание силлогизма. Содержание заключено в конкретных предметных постоянных S,M,P. Форма есть связь, между терминами в посылках. Важно соблюсти форму силлогизма, независимо от того, о чем говорит силлогизм.

Аксиома силлогизма. Силлогистическое умозаключение таково, что раз мы допустили посылки, то из них необходимо будет вытекать заключение. Формальным основанием является аксиома силлогизма:

Если А находится в В, а В нахо­дится в С, то, следовательно, А находится в С. Далее, если А на­ходится в В, но В находится вне С, то А также находится вне С.

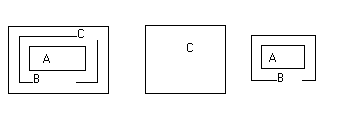
Смысл этой аксиомы за­ключается в следующем: Всё, что утверждается отно­сительно целого класса, утверждается и отно­сительно каждой вещи, которая содержится в этом классе, и наоборот: всё, что отрицается от­носительно целого класса, отрицается относи­тельно всего, что содержится в этом

классе.

Правила силлогизма. Рассмотрим, какие правила мы должны соблюсти при построении силлогизма, чтобы он был правилен, или, другими словами, каким условиям должен удовлетворять силлогизм, чтобы заключение было правильно. Первое правило: