5. Матрица путей

Для связного графа, вершины которого перенумеро­ваны, можно построить матрицу путей (или цепей) Р следующим образом: строки матрицы должны соответствовать путям из первой вершины в последнюю, а столбцы – ребрам графа. Следовательно, элемент мат­рицы принимает значение 1 или 0 в зависимости от того, принадлежит ли данное ребро данному пути или нет. Например, граф, изображенный на рис. 11, имеет матрицу путей между вершинами v₁ и v₅:

Рис.11. Граф для иллюстрации матрицы путей

2. Представление графов в виде списков

Можно связать список L_v с каждой вершиной v V. Таким образом, L_v – это список вершин, смежных с v (например, рис.12).

Возможно другое представление графов с помощью списка связей. Выбор представления зависит от используемых алгоритмов.

а) б)

Рис. 12. Полный граф (а) и его списки смежности (б)

3. Упорядоченные графы

Представление L_v вершин, смежных с v, в виде списка связей определяет «порядок» ребер, выходящих из v (рис. 13).

v₁

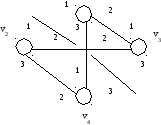
Рис. 13. Пример упорядоченного графа

Множество V = {v₁, v₂,…, v_n} вершин вместе с множеством {Lv₁, Lv₂, …, Lv_n} упорядоченных списков упорядоченных пар вершин называют упорядоченным графом.

Для того чтобы рассматриваемые структуры являлись графами, необходимо наложить некоторые условия на списки Lv:

• (v, v) Lv , v V;

• (w, u) Lw (u, w) Lu.

Граф, изображенный на рис. 13, может быть представлен в терминах упорядоченного графа следующим образом:

({v1, v2, v3, v4}, {((v1, v2), (v1, v3), (v1, v4)), ((v2, v1), (v2, v3), (v2, v4)), ((v3, v1), (v3, v2), (v3, v4)), ((v4, v1), (v4, v2), (v4, v3))}).

Упорядоченный граф определяет единственный неупорядоченный граф. Обратное утверждение неверно, так как в общем случае возможно много способов упорядочения графа.

5. Задачи нахождения путей в графах

Пусть G = (V, E) – ориентированный граф.

Рефлексивным и транзитивным замыканием графа G называется граф G^*, который содержит то же множество узлов, что и G, но в котором из v в w идет ребро тогда и только тогда, когда в G существует путь (длины 0 или больше) из v в w.

С задачей нахождения транзитивного замыкания тесно связана задача о кратчайшем пути.

Поставим в соответствие каждому ребру e графа G = (V, E) неотрицательную стоимость c(e). Стоимость пути определяется как сумма стоимостей ребер, образующих этот путь. Задача о кратчайшем пути состоит в нахождении для каждой пары узлов (v, w) пути наименьшей стоимости среди всех путей из v в w.

Наряду с понятием стоимости пути применяется понятие метки пути. Определим метку пути как произведение меток ребер, составляющих этот путь. Причем метки берутся в порядке прохождения ребер. В частности, метка пути нулевой длины равна 1. Для каждой пары узлов (v, w) определим c(v, w) как сумму меток всех путей между v и w. Назовем c(v, w) стоимостью прохождения из v в w.

Например, рассмотрим ориентированный граф, в котором каждое ребро помечено элементом полукольца S1 = ({0, 1}, +, , 0, 1) (рис. 14).

Метка пути v₁, v₂, v₃, равна 1. Простой цикл из v₂ в v₂ имеет метку 1 0 = 0. Вообще, каждый путь положительной длины имеет метку 0. Но стоимость пути нулевой длины из v₂ в v₂ равна 1. Следовательно, c(v₂, v₂)= 1.

Рис. 14. Метка пути и стоимость пути