2. Матрица циклов

Циклы C_i графа, изображенного на рис. 8, (перенумерованные, как показано на рис. 9), можно представить матрицей, каждая строка которой характеризует один из циклов:

Рис. 8. Несвязный циклический граф

Рис. 9. Нумерация циклов в графе

3. Матрица разрезов

Если задан связный граф G = (V, E) и множество его вершин разбито на два непустых подмножества W и W’, то множество ребер, соединяющих W с W’, называется разрезом. То есть, разрез (и в частности, простой разрез) является множеством ребер, соединяющих W и W’ , где {W, W’} является разбиением вершин связного графа на два непересекающихся непустых множества. Удаление разреза приводит к тому, что граф распадается на две или более компоненты. Удаление простого разреза разделяет граф точно на две компоненты.

В ориентированном графе дуги разреза могут быть разделены на два множества: дуги, направленные из W в W’, и дуги, направленные из W’ в W. Удаление первого множества разрывает все пути из W к W’, в то время как удаление последнего разрывает все пути из W’ к W.

Опишем теперь простые разрезы графа, изображен­ного на рис. 10, с помощью матрицы разрезов, каждая строка которой характеризует один простой разрез. В данном случае мы имеем следующие простые разрезы:

K₁ = {e₂}, K₂ = {e₃, e₇}, K₃ = {e₄, e₅},

K₄ = {e₃, e₄, e₅}, K₅ = {e₃, e₅, e₆}, K₆ = {e₄, e₆, e₇}, K₇ = {e₅, e₆, e₇}.

При этом матрица разрезов будет иметь вид:

e₃

e₆

e₄

e₂

e₇

e₅

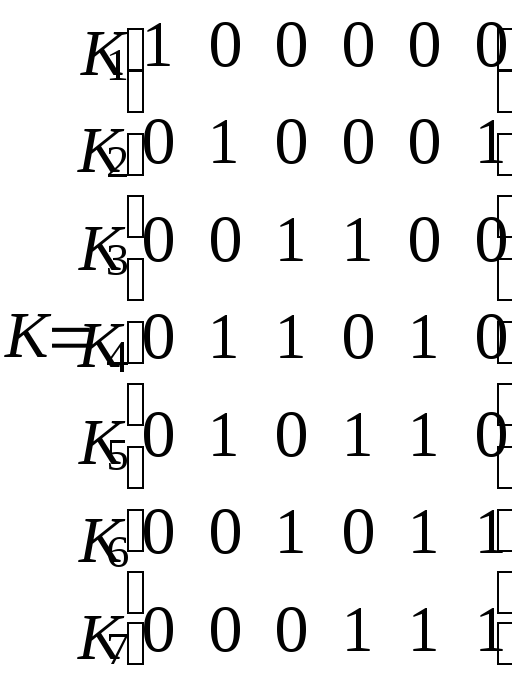
Рис. 10. Простые разрезы графа

4. Матрица смежности вершин

Для ориентированных и неориентированных графов можно определить матрицу смежности вершин (или про­сто матрицу смежности). Элемент на пересечении i-й строки и j-го столбца этой матрицы равен числу ребер, инцидентных одновременно i-й и j-й вершинам (или на­правленных от вершины i к вершине j в случае ориен­тированного графа). Таким образом, для ориентирован­ного графа, изображенного на рис. 8, можно построить матрицу смежности следующего вида:

В общем случае имеет место следующая теорема, касающаяся матрицы смежности V графа.

Теорема. Матрица Vⁿ дает число ориентирован­ных маршрутов длины п между любыми двумя верши­нами ориентированного графа.

Доказательство. Если а_ik – число дуг, соеди­няющих v_i с v_k, а а_kj – число дуг, соединяющих v_k с v_j, то а_ikа_kj есть число различных ориентированных марш­рутов, каждый из которых состоит из двух дуг, соеди­няющих v_i с v_j, и проходящих через v_k. Если это произ­ведение просуммировать по всем k, т. е. по всем про­межуточным вершинам, то получим число ориентирован­ных маршрутов длины 2 между вершинами v_i и v_j. Используем теперь а_ij для получения а_ijа_jm. В результате найдем число различных ориентированных маршрутов длины 3 между вершинами v_i и v_m проходящих через v_j, и так далее. Таким образом, если предположить, что теорема верна для

, то элементы матрицы дадут число ориентированных маршрутов длинып между соответствующими вершинами.

Матрица вершин, как в случае ориен­тированных, так и в случае неориентированных графов имеет неотрицательные элементы. Нулевой элемент оз­начает, что вершина, соответствующая строке рассмат­риваемого элемента, не связана ребром с вершиной, со­ответствующей столбцу. Однако эти вершины могут быть связаны путем (или цепью) определенной длины. Может оказаться, что V^m>0 для некоторого целого m 1 , т. е. после возведения V в степень m все ее эле­менты становятся положительными.

В этом случае каждая вершина достижима из лю­бой другой вершины ориентированным маршрутом, со­стоящим из т дуг, и граф, соответствующий V^m, явля­ется полным (действительно, он имеет дугу, направлен­ную от любой другой) и имеет петли у каждой вершины.