Анализ точности

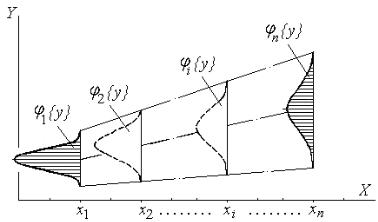
Эксперимент, при котором значения Y определяют при целенаправлен-

ном изменении W, называют активным, т.е. значения W устанавливаются по усмотрению экспериментатора.

2. Корреляционная зависимость. Корреляционной называется зависи-

мость между двумя случайными величинами, при которой вследствие изме-

нения одной величины (аргумента X) изменяется только математическое ожидание другой (функции Y). В отличие от регрессионной зависимости здесь аргумент – случайная величина. Таблица и график, характеризующие корреляционную зависимость, имеют следующий вид (табл. 2.2 и рис. 2.8).

Рис. 2.8. Пример корреляционной линейной зависимости (может быть

криволинейная)

3. Скедастическая зависимость. Скедастической называется зависи-

мость между двумя переменными, если одна из них Y, являясь случайной ве-

личиной, реагирует на изменение другой величины – аргумента (как неслу-

чайной W, так и случайной X) только изменением своей дисперсии.

21

Эту зависимость также изобразим в виде таблицы (табл. 2.3).

и графика (рис. 2.9).

Рис. 2.9. Пример скедастической зависимости

2.2.3. Построение математической модели точности ТП

Математическую модель будем получать в виде аналитических выра-

жений, устанавливающих взаимосвязи между законами распределения, чи-

словыми характеристиками и практическими полями рассеивания погрешно-

стей входных и выходных параметров.

Выделим две группы моделей:

1) модели, построенные на основе известной функциональной зависи-

мости между входными и выходными переменными; 2) модели, построенные исходя из предположения наличия вероятност-

ной (стохастической) зависимости между входными и выходными парамет-

рами.

22

Первая группа моделей

В основе построения моделей этой группы могут быть известные зави-

симости, типа (2.1), либо полиномиальные зависимости вида

где b0 , bi , bij , bii – постоянные величины, представляющие собой коэффициен-

ты ряда Тейлора, т.е. значения частных производных в точке, вокруг которой осуществляется разложение неизвестной функции:

достаточно полно разработаны. Неизвестные коэффициенты определяются при обработке данных активного (реже пассивного) полного или дробного факторного эксперимента.

Итак, независимо от способа получения в качестве исходной формулы имеем функциональную зависимость

Y f {X1, X 2 , ..., Xi , ..., X N },

где Y – выходной параметр;

Xi – входные параметры;

Gi – области их определения.

Кроме того, должны быть входных параметров.

Начнем с более простого случая.

Дано:

1)Y f {X }, где X и Y – случайные величины;

2) x {x}– плотность вероятности распределения случайной величины X.

Требуется определить y {y} – плотность вероятности распределения

случайной величины Y. Из формулы для могут быть найдены выраже-

ния для математического ожидания m{Y}, дисперсии ζ2 {Y} и практического

23

Полученный закон распределения называется распределением Симп-

сона и имеет вид равнобедренного треугольника (рис. 2.10).

Рис. 2.10. Распределение Симпсона

Известно, что если число независимых между собой случайных сла-

гаемых, распределенных по закону равной вероятности с пределами

1 xi 1, будет стремиться к бесконечности, то распределение функции Y

будет приближаться к нормальному с пределами y . Это еще раз подтверждает, что формула Гаусса – всего лишь математическая абстракция

(как и все математические модели), а не закон, которому подчиняются собы-

тия объективного мира.

25

Полученная формула есть не что иное, как закон Гаусса с математиче-

ским ожиданием m{Y } m{X1} m{X 2 } и средним квадратическим отклонени-

ем

{Y } 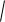2 {X 1} 2 {X 2 } .

Из рассмотренного примера следует вывод: если случайная величина Y

представляет собой линейную функцию от случайных независимых между собой параметров Xi , распределенных по нормальному закону, то распреде-

чивым законом (т.е. воспроизводящим себя при компонировании).

В задачах анализа точности технологических процессов часто встреча-

ется зависимость вида U 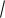X 2 Y 2 , где X и Y – независимые случайные ве-

личины, распределенные обычно по нормальному закону. Такую модель применяют для описания различного рода радиальных отклонений, например смещений центров отверстий относительно своих номинальных положений;

в этом случае величины X и Y представляют собой погрешности смещений центров отверстий вдоль соответствующих осей координат. Плотность рас-

пределения величины U , называемого законом Максвелла, имеет вид

0 u ,

27

индекс «ср» обозначает, что в выражение для частной производной после дифференцирования должны быть подставлены средние значения всех аргу-

ментов (обычно m{Xi}).

Если входные переменные связаны между собой корреляционной зави-

симостью, то в формуле для дисперсии появятся дополнительные члены.

В случае линейного вида функции Y f {X1, X 2 , ..., Xi , ..., X N } прибли-

женные выражения для математического ожидания и дисперсии становятся точными.

Пример 5. Получим формулы для приближенного определения число-

вых характеристик сопротивления тонкопленочного резистора (2.1)

Используя полученные выражения, рассчитаем m{R} и ζ2{R} при сле-

дующих исходных данных:

m{ } 5 10 5 Ом∙м; m{l} 5 10 3 м; m{b} 5 10 4 м; m{h} 10 7 м;

29

распределение параметров ρ, l, b и h в пределах 3 % относительно их сред-

них значений (математических ожиданий) принять по закону равной вероят-

ности. Получаем

(метод Монте-Карло). В этом методе в качестве исходного распределения используется специальная программа «Датчик случайных чисел», которая формирует последовательность случайных чисел, распределенных по закону равной вероятности в диапазоне 0…1 (случайная величина ). Дальнейшее моделирование случайных величин может осуществляться по алгоритмам,

приведенным в табл. 2.4[10].

Таким образом, на первом шаге получаем значения ρ1, l1, b1 и h1 в соот-

ветствии с их законами распределения. Подставляем эти значения в формулу

(2.1) и рассчитываем величину R1. Повторяя эти действия (которые обычно называют итерациями) многократно, получим совокупность значений Ri

i 1, N , на основании которых строится гистограмма и определяются число-

вые характеристики.

30