
Анализ точности
.pdfливающие взаимосвязи между законами распределения, числовыми характе-
ристиками и практическими полями рассеивания входных (в примере ρ, l, b и h ) и выходных (в примере – R) параметров.
Ко второй группе относят задачи, при постановке которых зависимость между входными и выходными параметрами еще до конца не выяснена и ее требуется установить и исследовать. Такие задачи при формализации ТП производства ЭС встречаются наиболее часто.
2.2. Этапы и методы построения математических
моделей точности технологических процессов
Этапы:
1.Отбор факторов (входных переменных).
2.Установление типа зависимости между исходными факторами и по-
грешностями обработки.
3.Построение математической модели.
4.Проверка адекватности разработанной модели и реального техноло-
гического процесса.
2.2.1. Отбор факторов (входных переменных)
Успех исследования в значительной степени определяют отбор и опи-
сание исходных факторов. Входные переменные для включения их в матема-
тическую модель должны выбираться на основе предварительного теорети-
ческого анализа, исходя из целей и задач исследования. Как правило, на этом этапе анализируются и обобщаются результаты ранее проведенных исследо-
ваний таких же процессов или процессов-аналогов.
При отборе факторов к ним предъявляется ряд требований. Прежде всего, технологические факторы должны быть количественно измерены. Ес-
ли фактор характеризуется только качественными показателями, то учет его влияния, как правило, затруднен либо вообще невозможен.
11
Перечень входных переменных должен включать в себя важнейшие факторы, оказывающие наиболее существенное влияние на точность обра-
ботки. Это требование вытекает из того, что при моделировании необходимо абстрагироваться от влияния несущественных факторов. Кроме того, модель должна быть простой и наглядной.
Исходные факторы не должны находиться между собой в точной
(функциональной) зависимости, так как существование функциональных и близких к ним связей показывает, что они характеризуют одну и ту же сто-
рону изучаемой первичной погрешности и, следовательно, в какой-то мере дублируют друг друга.
На начальной стадии исследования большое значение приобретает во-
прос о правильной классификации исходных факторов и выбора для них ма-
тематической модели. Обычно факторы классифицируют на систематиче-
ские (неслучайные) и случайные.
Систематические факторы, в свою очередь, делятся на постоянные,
принимающие вполне определенные числовые значения при обработке каж-
дого последующего элемента, и переменные, закономерно изменяющиеся при переходе от одного элемента к другому. Случайные факторы могут при-
нимать то или иное числовое значение, заранее не известно какое именно,
при повторном воспроизведении комплекса условий их возникновения. Эти факторы могут быть выражены случайными величинами или случайными функциями.
Иногда один и тот же фактор в разных задачах может рассматриваться неодинаково. Например, если для одной задачи разброс значений этого фак-
тора можно считать несущественным, то в модель его включают как кон-
станту, в противном случае – как переменную или случайную величину.
Операционные погрешности, в свою очередь, также относят либо к систематическим (постоянным или переменным), либо к случайным, в зави-
симости от того, влияние каких из перечисленных факторов является доми-
нирующим в их появлении.
12

На стадии отбора факторов требуется установить их области определе-
ния. Для случайных факторов это связано с установлением законов распре-
деления.
В качестве математических моделей для описания случайных факторов при решении задач анализа точности технологических процессов наиболее часто используются теоретические законы распределения, такие как закон равной вероятности, закон Гаусса и др.
Закон равной вероятности описывает распределение как непрерывной,
так и дискретной случайной величины, которая может принимать допусти-
мые значения с равной вероятностью.
Плотность вероятности распределения непрерывной случайной вели-
чины (например, X) может быть выражена:
а) аналитически
|
0 |
при x<a, |
|
1 |
|
{x} |
|
при a x b, |
|
||
b a |
при x>b, |
|
|
0 |
|
где b – a = 2l – область возможных значений случайной величины X;
математическое ожидание и дисперсия соответственно равны
m{X } |
a b |
|
|
(b a)2 |
l 2 |
|||
|
; |
2{X } |
|
|
|
; |
||
2 |
12 |
3 |
||||||
|
|
|
|
|
||||
б) графически (рис. 2.1).
Рис. 2.1. Плотность вероятности равномерного распределения непрерывной
случайной величины
13

Плотность вероятности распределения дискретной случайной величи-
ны (например, X) может быть выражена:
а) в виде таблицы
p(xi) |
1/n |
1/n |
1/n |
1/n |
1/n |
|
|
|
|
|
|
X |
x1 |
x2 |
x3 |
. . . |
xn |
|
|
|
|
|
|
б) графически (например, в виде столбиковой диаграммы, рис. 2.2).
Рис. 2.2. Плотность вероятности равномерного распределения дискретной
случайной величины
Закон равной вероятности обычно рассматривается как исходный для получения некоторых других распределений аналитически или моделирова-
нием на ЭВМ (параграф 2.2.3).
Закон нормального распределения (закон Гаусса) описывает распреде-
ление непрерывной случайной величины, которая может принимать значения в диапазоне от до , причем ее отклонения от некоторого среднего значения (математического ожидания) подчиняются следующим правилам:
– отрицательные и положительные отклонения, равные по модулю,
равновероятны;
– чем больше (по модулю) отклонение, тем оно менее вероятно.
Плотность вероятности нормального распределения случайной вели-
чины (например, X) имеет вид:
14

а) аналитически
|
1 |
|
|
|
(x m{X })2 |
|
||||
{x} |
|
|
|
exp |
|
|
|
|
, |
|
|
|
|
2 |
2 |
|
|||||
{X } 2 |
{X } |
|||||||||
|
|
|
|
|
|
|||||
где m{X } и 2{X} соответственно математическое ожидание и дисперсия;
б) графически (рис. 2.3).
Рис. 2.3. Плотность вероятности распределения Гаусса
В технических приложениях из теоретических законов распределения закон Гаусса является самым распространенным. Его обычно используют для описания разброса значений параметров изделий, изготовленных в условиях серийного и массового производства. Часто гауссов закон встречается при обработке результатов различного рода измерений [8].
Применяя закон Гаусса, исследователи часто совершают две основные ошибки:
1) не всегда достаточно обосновывают выбор формулы Гаусса в каче-
стве математической модели; 2) не учитывают, что формула Гаусса – это всего лишь математическая
модель.
Как правило, основным (а часто и единственным) доводом в пользу выбора нормального распределения является колоколообразная форма экспе-
риментальной гистограммы (например, рис. 1.1). При этом совершенно не учитывается тот факт, что погрешности изготовления или измерения не мо-
гут принимать сколь угодно большие (по модулю) значения. Формула Гаусса достаточно хорошо согласуется с экспериментом в диапазоне значений, не
15

превышающих 3 {X } (относительно m{X } ). В этот диапазон попадает
99,73% всех значений случайной величины (например, X). Но если по этой модели строить прогнозирующие расчеты вне этого диапазона, то результат будет резко расходиться с реальностью (см. подглаву 5.5).
Большинство исследователей, применяя нормальный закон распре-
деления, предполагают его справедливость само собою разумеющейся.
В действительности дело обстоит сложнее. В свое время по поводу это-
го закона было достаточно точно, хотя не без сарказма, сказано, что
«экспериментаторы верят в него, полагаясь на доказательства матема-
тиков, а математики – полагаясь на экспериментальное обоснова-
ние»[8]. Что же касается экспериментальных обоснований, то они ниче-
го не дают, кроме гистограммы, и всегда можно подобрать достаточно хорошую интерполирую функцию, которая для данного случая будет представлять более адекватную модель. Например, при реш ении
некоторых практических задач ( см. подглаву 5.5) лучшее совпадение с экспериментом дает применение распределения.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
при |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x m{X } |
|
|
2 |
при |
||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|||
|
|
|
|
|
{X } |
|
|
|
||||||
{x} |
16 {X } |
|
|
|
|
|
||||||||
|
1 |
|
|
x m{X } |
2 |
|
|
|||||||
|
|
|
|
|
|
при |
||||||||
|
|
|
|
3 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||
|
8 {X } |
|
{X } |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x m{X } |
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
3 |
|
|
при |
|||
|
|
|
|
|
|
|
|
|
|
|||||
16 {X } |
{X } |
|
|
|
|
|
||||||||
|
|
|
|
|
||||||||||
x m{X } |
3 и |
x m{X } |
3, |
|||
{X } |
|
{X } |
|
|||
|
|
|||||
3 x m{X } 1,
{X }
1 |
x m{X } |
1, |
(2.2) |
|||
|
|
|||||
|
|
{X } |
|
|
|
|
1 |
x m{X } |
|
3. |
|
||
{X } |
|
|||||
|
|
|
|
|||
Сравнение кривых Гаусса и (2.2) приведено на рис. 2.4.
Распределение (2.2) практически не отличается от нормальн ого,
но в границах 3 {X } находится 100 % всех значений величины X.
Ошибочному выбору математической модели нередко способствуют приводимые в технической литературе (в т.ч. и в фундаментальной, напри-
мер [11, с. 49, 51] ) некорректные высказывания типа «погрешности подчи-
16

няются» (выделено автором) тому или иному закону распределения (Гаусса,
Релея и т.д.). Погрешности (какими бы они ни были) подчиняются своим за-
конам (законам объективного мира)! А теоретические законы распределения
(в т.ч. и Гаусса) – это лишь применяемые нами математические модели, ко-
торые (в силу своего определения) не могут быть абсолютно точными (адек-
ватными).
Рис. 2.4. Сравнение распределения Гаусса (1) и распределения (2. 2) -2
2.2.2. Установление типа зависимости между исходными
факторами и погрешностями обработки
Реальные процессы, происходящие в объективном мире. Характеризу-
ются высокой сложностью, взаимосвязанностью и взаимообусловленностью.
В процессе построения математических моделей приходится абстрагировать-
ся от действительного положения вещей и учитывать только наиболее суще-
ственные стороны изучаемых явлений. Поэтому при анализе и формализа-
ции технологических процессов предполагается, что исследуемые величины либо независимы между собой, либо связаны одной из следующих зависимо-
стей:
–функциональной;
–вероятностной (стохастической).
Рассмотрим эти виды связей применительно к двум переменным: X
(или W), с одной стороны, и Y – с другой.
17
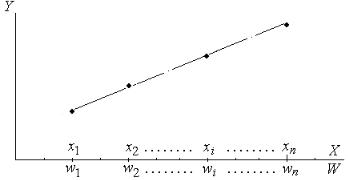
Функциональная зависимость. При функциональной зависимости между двумя переменными, изменяющимися как систематически, так и слу-
чайно, каждому значению одной величины (аргумента) соответствует одно вполне определенное значение другой величины (функции), т.е. влиянием факторов Z можно пренебречь. Это определение можно проиллюстрировать таблицей, приведенной ниже, и графиком (рис. 2.5),
|
Вход |
|
Выход |
|
|
|
|
x1 |
или |
w 1 |
y1 |
x2 |
или |
w2 |
y2 |
|
. . . |
|
. . . |
xi |
или |
wi |
yi |
|
. . . |
|
. . . |
xn |
или |
wn |
yn |
|
|
|
|
где xi – конкретные значения случайной величины вектора X (обычно x1, x2, xi, xn представляют собой центры интервалов, на которые разбивают диапазон наблюдаемых значений X);
wi – конкретные значения неслучайной величи-
ны вектора W;
yi – вполне определенные значения вектора Y.
Рис. 2.5. Пример функциональной линейной зависимости (может быть криволинейная)
В условиях серийного и массового производства на параметры качест-
ва электронных средств оказывает влияние значительное число неконтроли-
руемых или трудно учитываемых факторов. Для описания влияния этих фак-
торов при построении математических моделей подобных процессов наибо-
лее подходит использование вероятностной (стохастической) зависимости.
Вероятностная (или стохастическая) зависимость. Зависимость между двумя переменными называется стохастической (вероятностной), если одна из них Y, являясь случайной величиной, реагирует на изменение другой
18

величины – аргумента (как неслучайной - W, так и случайной – X) изменени-
ем своего закона распределения. Другими словами, в общем случае вероят-
ностной зависимости, при изменении значения одной величины (аргумента)
изменяется условный закон распределения другой величины (функции). Для вероятностной зависимости влияние факторов Z существенно и пренебрегать им нельзя. Это определение вновь проиллюстрируем таблицей и графиком
(рис. 2.6).
|
Вход |
|
Выход |
|
|
|
|
x1 |
или |
w 1 |
φ1{y} |
x2 |
или |
w2 |
φ2{y} |
|
. . . |
|
. . . |
xi |
или |
wi |
φ i{y} |
|
. . . |
|
. . . |
xn |
или |
wn |
φ n{y} |
|
|
|
|
где φ i{y} – условный закон (плотность вероятности)
распределения случайной величины Y при значениях xi (или wi ).
Для значений xi (или wi ), воспроизводимых несколько раз (значения wi мы устанавливаем сами целенаправленно, а xi представляют собой значе-
ния, попавшие в соответствующий диапазон со средним значением, равным xi), мы получаем множество значений величины Y (что позволяет рассматри-
вать ее как случайную величину).
Рис. 2.6. Пример вероятностной (стохастической) зависимости
Таким образом, наблюдаемое множество значений Y для i-й точки мо-
жет рассматриваться как условное распределение величины Y с плотностью вероятности φ i{y} . В общем случае вероятностной зависимости при перехо-
де от одних значений xi (или wi ) к xi+1 (или wi+1) мы получаем новый закон распределения φ i+1{y}, при этом может изменяться как сам закон распреде-
19
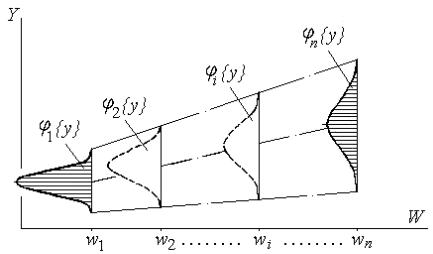
ления (аналитически и графически), так и его числовые характеристики: ма-
тематическое ожидание m i+1{y} и дисперсия ζ2 i+1{y}.
Некоторые частные случаи вероятностной зависимости
1. Регрессионная зависимость. Регрессионной называется зависимость между неслучайной величиной W (аргументом) и случайной величиной Y
(функцией), при которой при изменении аргумента изменяется только мате-
матическое ожидание функции, а условное распределение величины Y (т.е.
при любых значениях W) нормальное с постоянной дисперсией. Как и ранее представим регрессионную зависимость в виде таблицы (табл. 2.1) и графи-
чески (рис. 2.7).
|
|
|
|
Таблица 2.1 |
||
|
|
|
|
|
|
|
Вход |
|
|
Выход |
|
|
|
|
|
|
|
|
|
|
w 1 |
φ1{y} |
|
|
m1{y} |
|
|
w2 |
φ2{y} |
Гаусса |
|
m2{y} |
const}≈{y |
|
. . . |
. . . |
|
. . . |
|
||
|
|
|
|
|||
wi |
φ i{y} |
Закон |
|
m i{y} |
|
|
. . . |
. . . |
|
. . . |
ζ |
|
|
|
|
|
|
|
2 |
|
wn |
φ n{y} |
|
|
m n{y} |
|
|
|
|
|
|
|
|
|
Рис. 2.7. Пример регрессионной линейной зависимости (может быть криволинейная)
20
