Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Chast_3_novyy

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

4.66 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2122 / 2522 23 24 25 > Следующая >>>

lim1 3x 1 . x 0 1 x 1

14. Используя преобразования и эквивалентные бесконечно малые функции,

	2ln x 1 1
вычислить предел lim		.

x 0	x


15. Вычислить lim f g x , если		f x ex , а g x tg						.
15. Вычислить lim f g x , если		f x ex , а g x tg						.
x							x
16. Найти точки разрыва функции, исследовать их характер, в случае
устранимого разрыва доопределить функцию «по непрерывности»:
1 cos x				sin x
1 cos x				sin x
а) f x			; б) f x			.
	x	x 1

					x


		Вариант 22
1. Написать формулу общего члена последовательности							0,		3	,	2	,		5	,
1. Написать формулу общего члена последовательности							0,			,	9	,	16		,
							4				9		16

2. Указать, какие из заданных последовательностей будут ограниченными, бесконечно большими, бесконечно малыми

x cos3	n 1 ;	x	1
x cos3	n 1 ;	x
n		n		1
			sin
			sin
			n

; xn n 1 .

						2										1		2
			2n					n
			2n					n								2
3.	Вычислить предел	lim														2						.
3.	Вычислить предел	lim				3n 4n2																.
		n				3n 4n2
			3								4			5n4 2									.
4.	Вычислить предел	lim	3		n 1						4			5n4 2
4.	Вычислить предел	lim
		n					4 n4 1 1
5.	Вычислить предел	lim	cos2 2n										.
5.	Вычислить предел	lim			2n 1								.
		n			2n 1
6.	Вычислить предел lim			52n 63n													.
6.	Вычислить предел lim																.
	n 7 63n 2 5n
7.	Вычислить предел lim				n! 3 n														.
7.	Вычислить предел lim																		.
	n 3 n 1 ! 4
				n2 1 n
8.	Вычислить предел lim											.
8.	Вычислить предел lim						2		2			.
		n		n					2
						1									1					.
9. Вычислить предел		lim				1						x			1
9. Вычислить предел		lim				1 24
		x				1 24								x
10. Вычислить предел		lim						x2 3x 2													.
10. Вычислить предел		lim																			.
		x 2								x						2
										x						2

194

	x
11. Вычислить предел	x			2 x2 x			2 x 2 1	.
11. Вычислить предел	lim			2 x2 x			2 x 2 1	.
		2 x x2				x
12. Вычислить предел	lim					.
12. Вычислить предел	lim		2 x		2	.
	x		2 x
	x

13. Используя эквивалентные бесконечно малые функции, вычислить предел

lim sin ln 1 x . x 0 sin5x

14. Используя преобразования и эквивалентные бесконечно малые функции,

вычислить предел lim	1 cos 2x			.
вычислить предел lim				.
x 0		3x2
											g x
																			2
15. Вычислить lim f g x , если f					x tg				, а							1 x				.
15. Вычислить lim f g x , если f					x tg		x 2		, а							1 x				.
x							x 2
16. Найти точки разрыва функции, исследовать их характер, в случае
устранимого разрыва доопределить функцию «по непрерывности»:
а) f x		arctgx	; б)		f x			1 x			.
		arctgx						1
						x				x
		x				x				x
		x
			Вариант 23
1. Написать формулу общего члена последовательности												3	,	3	, 0,		3	,	3		, 0,
1. Написать формулу общего члена последовательности											4		,		, 0,			,			, 0,
											4		4			4			4

2. Указать, какие из заданных последовательностей будут ограниченными,

бесконечно большими,

бесконечно малыми

n 1

;

x ln 3 cos n ;

x 1

n 2 3 2 n 2 3

3. Вычислить предел lim

n3 n2 n 1

4. Вычислить предел lim 3 n n 1 . n 3 n 3 4n 1

5. Вычислить предел lim3n sin n 2 .

Вычислить предел lim

8 3n 2

n 5 3n 1 4n 1

Вычислить предел

lim

2n ! 3n !n

3n 1 !

2n2

Вычислить предел lim

9. Вычислить предел

lim

3x x 2

x 5 3x 1 2

195

10. Вычислить предел

lim

x 1

1 x2

11. Вычислить предел

3 2x

1 3

2x 1

lim 3

2x 3 x

12. Вычислить предел

lim

2x 1

13. Используя эквивалентные бесконечно малые функции, вычислить предел

lim		1 sin x		.

x
		x
	2
			2

14. Используя преобразования и эквивалентные бесконечно малые функции,


вычислить предел	lim	arctg x 1

	x 0		1	.

		1 ln ex

15.	Вычислить lim g f x , если				f x		cos x	, а g x						.
15.	Вычислить lim g f x , если				f x			, а g x						.
		x 0					x 1		1 x
16.	Найти точки разрыва функции, исследовать их характер, в случае
устранимого разрыва доопределить функцию «по непрерывности»:
а) f x		sin sin x	; б) f x ln	ex 1		.
		sin sin x

		x
		x
			Вариант 24
1. Написать формулу общего члена последовательности									1	,		4	,		9	,	16	,
1. Написать формулу общего члена последовательности									2	,	9		,		28	,	65	,
									2		9				28		65

x tg

;

1 1 n

;

x ln

2 cos n

Вычислить предел

lim

3 n 2 4 n3 2

n n4 16n8 n6 1

4 n3

Вычислить предел

lim

n 2 4 2n3 n

Вычислить предел lim

n2 cos

n3 1

Вычислить предел lim

4 32n 4n

n 5 4n 2 32n

Вычислить предел lim 2n2 ! 2n2

1 ! .

1 2n

196

8.Вычислить предел

9.Вычислить предел


	2 n		n
lim		.
lim		.
n	3 n

x lim

x x 1

10. Вычислить предел

lim

x 1 1

x 0

x 1 1

11. Вычислить предел

lim

3 1 x

12. Вычислить предел

lim 1 x3

13. Используя эквивалентные бесконечно малые функции, вычислить предел

lim ln 1 e x .

x ex 3

14. Используя преобразования и эквивалентные бесконечно малые функции,

вычислить предел lim	x		tgx .

		2
x

2

15. Вычислить lim g f x , если

x 0

f x ln x 1 , а g x arctgx .

16. Найти точки разрыва функции, исследовать их характер, в случае устранимого разрыва доопределить функцию «по непрерывности»:

	x	f x	1 x
а) f x 2x 1 ; б)			1 x					.
			1
					1		x
				x
				x
						Вариант 25
1. Написать формулу общего члена последовательности									1	,	3	,	1	,	1	,	1
1. Написать формулу общего члена последовательности										,	5	,	7	,		,
					3						5		7	3		11

2 1 n

;

n 1

n2 1

2n 1

1 n 2

Вычислить предел

lim

n 2 3

n n 1 4 n 1 4

Вычислить предел

lim

5 n3 6 n5

n 4n3 1 3 1 2n5 1

197

5.	Вычислить предел lim											n							.
5.	Вычислить предел lim																		.
		n		n		2	1							1
										1 cos
										1 cos
														n
			2			n2				n2
6.	Вычислить предел lim		2				3						.
6.	Вычислить предел lim						2						.
		n		2 5 3n							1
7.	Вычислить предел lim				n 1 ! n 2 !												.
7.	Вычислить предел lim		n 2 ! n n 1 !														.
		n	n 2 ! n n 1 !
			n 1 n 1
8.	Вычислить предел lim								.
8.	Вычислить предел lim								.
		n	n 2									x		2 2
9.	Вычислить предел	lim						x 1				x		2 2				.
9.	Вычислить предел	lim					2											.
		x					2				x4 1 1
10. Вычислить предел				lim				x3 x2 2x							.
10. Вычислить предел				lim											.
				x 1							x 1
11. Вычислить предел					lim					x2 9 3						.
11. Вычислить предел					lim											.
					x 0								x

x 2 x

12. Вычислить предел lim . x x 1

13. Используя эквивалентные бесконечно малые функции, вычислить предел


		1 x
	ln

lim		1 x	.

x 0		x

14.

Используя преобразования и эквивалентные бесконечно малые функции,

вычислить предел

lim

cos x sin x 1

x 0

x2 x

15.

Вычислить

f x

, если

f x arctgx , а g x sin x .

lim g

16.

Найти точки разрыва функции, исследовать их характер, в случае

устранимого разрыва доопределить функцию «по непрерывности»:

а) f x

; б) f

x 2

cos x sin x

198

Расчетная работа № 3. Часть 2. Варианты

Вариант 1

1. Найти производную функций:

а)

y tg ln x 2x ; б)

y 2cos 3x ; в)

; г) y ex arcsin

x .

1 x2

Найти производную функции y sin xctgx

в точке x

Найти производную

, если

y x в точке

1 t .

t 2

1 t2

4.	Найти y 50 x , если	y x xe2x .
5.	Найти дифференциал неявно заданной функции y x :
		y4 sin yx x2	2 .

6.С помощью первого дифференциала вычислить приближённо значение arccos0.6 .

7.Найти предел lim ln x 2x 1 .

x 0 0

8. Написать уравнение касательной к кривой y arctgx в точке x 3 .

9. Написать формулу Тейлора 3-го порядка для функции y	1	в точке

2 x2

x 0 .

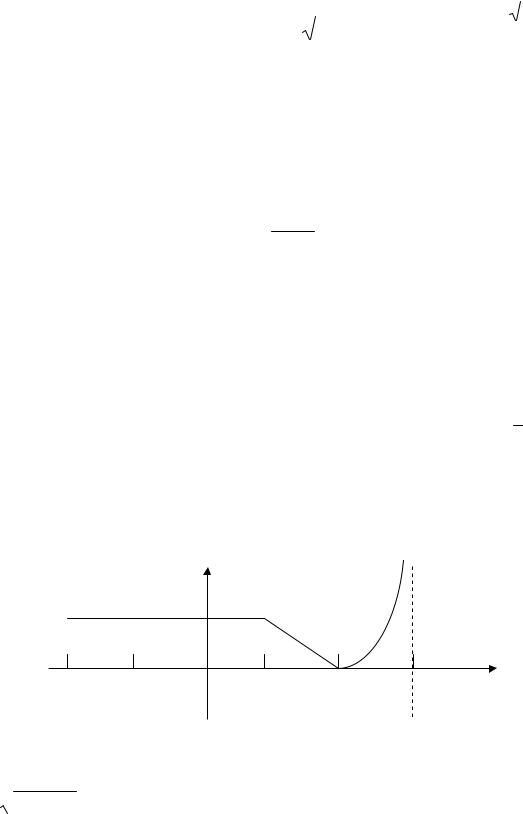
10. По графику функции

построить график производной.

11. Провести полное исследование и построить график функции

y 3 x2 2x .

199

Вариант 2

Найти производную функций:

x2 sin x

cos x 1

а)

y сtg e

3x ; б) y 3

; в)

; г)

ln x

x 3

Найти производную функции

y xtgx

в точке x

Найти производную

x 1, если

y x в точке

1 t

ln tg t

Найти y 40 x , если

y x x sin 2x .

Найти дифференциал неявно заданной функции y x :

xy4 ex y3 2 .

6.С помощью первого дифференциала вычислить приближённо значение arcsin 0.05 .

7.Найти предел lim x ln arctgx .

	x 0 0
8.	Написать уравнение касательной к кривой y ln 1 x в точке x 0.
9.	Написать формулу Тейлора 3-го порядка для функции y	sin x	в точке

		x

x .

10. По графику функции

построить график производной.

11. Провести полное исследование и построить график функции y ex .

x 1

200

Вариант 3

Найти производную функций:

y ln sin x 3

; б)

а)

y 58tg2 x ;

в)

x 1

; г) y cos 5 x arccos

x 1

Найти производную функции

y x2

1 arctgx

в точке x

Найти производную

y x в точке x 0 , если

2 sint t .

y cost t

Найти y 50 x , если

y x 1 x cos x .

Найти дифференциал неявно заданной функции y x :

ctg y2 x 3xy 5y 1.

С помощью первого дифференциала вычислить приближённо значение

arctg0.02 .

Найти предел lim 1 5x

Написать уравнение касательной к кривой y sin x в точке x

Написать формулу Тейлора 3-го порядка для функции y

cos x

в точке

x .

10. По графику функции

построить график производной.

11. Провести полное исследование и построить график функции

y		x		2
			.

	x 1

201

Вариант 4

Найти производную функций:

y arctg sin x 1 ; б)

y 3ln2 ln x ; в)

а)

1 x2

;

ctg2

г) y 1 x cos 2 x .

tg x 2

Найти производную функции y arccos x x 1

в точке x 0 .

Найти производную

x 1, если

y x в точке

1 t .

Найти y 60 x , если

y t2

y x x ln x .

Найти дифференциал неявно заданной функции y x :

xy2 sin xy x .

6. С помощью первого дифференциала вычислить приближённо значение arcctg0.98 .

			1
7.	Найти предел lim		sin

			x .
		x 1
	x
8.	Написать уравнение касательной к кривой y tgx в точке x					.

			6
9.	Написать формулу Тейлора 3-го порядка для функции y			tgx	в точке

				x

x .

10. По графику функции

построить график производной.
11. Провести полное исследование и построить график функции y	x4 1 .

202

Вариант 5 1. Найти производную функций:

а) y ln 1 ln2 x ; б)

г) y x 2 2 x arccos

						ctg3x	1
			arctg 1 3x ;			ctg3x	x2
y 5		x			в) y		x2	;
y 5					в) y	sin x 4x		;
	x					sin x 4x
	x
				.
	x 1			.
	x 1

2.	Найти производную функции y cos x tgx в точке x					.
2.	Найти производную функции y cos x tgx в точке x					.
				4
3.	Найти производную		x 2, если
3.	Найти производную	y x в точке	x 2, если
				1
				1
		x	3 t
		x	3 t		t .
			1		t .
		y	1
		y
	Найти y 45 x , если		1		t
4.	Найти y 45 x , если	y x 2x 1 ln x 1 .
5.	Найти дифференциал неявно заданной функции y x :
		xy2 yx2 ln x y 2 .
6.	С помощью первого дифференциала вычислить приближённо значение
arctg1.05 .
7.	Найти предел lim ln x e x .
	x
8.	Написать уравнение касательной к кривой y cos x в точке x								.
8.	Написать уравнение касательной к кривой y cos x в точке x								.
				4
9.	Написать формулу Тейлора 3-го порядка для функции y						ctgx	в точке
9.	Написать формулу Тейлора 3-го порядка для функции y							в точке
							x

x .

10. По графику функции

построить график производной.
11. Провести полное исследование и построить график функции y	x3 1 .

203

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2122 / 2522 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.11.2018523.26 Кб18chast2.doc
#
06.11.2018662.53 Кб16chast3.doc
#
06.11.2018832 Кб10Chast5.doc
#
29.03.20154.38 Mб170Chast_10_TV.pdf
#
23.02.20154.6 Mб27Chast_2_VA_i_AG.pdf
#
23.02.20154.66 Mб30Chast_3_novyy.pdf
#
23.02.2015220.05 Кб13Chast_7_4_RR.pdf
#
23.02.20152.2 Mб32Chast_8_Teoria_polya.pdf
#
01.05.20252.76 Mб1Chemical engineering.doc
#
01.03.2025457.22 Кб0chertov9-46.doc
#
22.02.20151.39 Mб28chistovik.docx