Chast_3_novyy

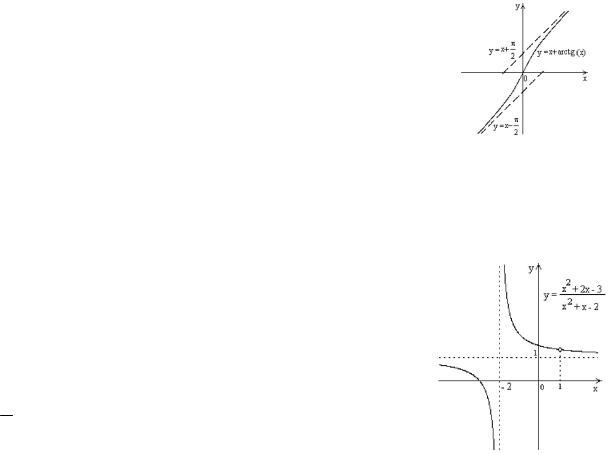
ПРИМЕР.

Найдите

асимптоты

графика функции

y x arctgx .

lim

x arctgx

k lim

x arctgx

k 1,

x

x

x

x

b

lim arctgx

, b

lim arctgx

,

x

2

x

2

график имеет две несовпадающие наклонные асимптоты:

левую y x

и правую y x

.

2

2

x2 2x 3

ПРИМЕР. Постройте график функции y

без использования произ-

x2

водной. Преобразуем выражение:

x 2

x

2

2x 3

x 1

x 3

x

2

2x

3

x

3

( x 1),

,

x2 x 2

x 1 x 2

x2 x 2

x 2

x 3

1 x 2

1

1, т.е.,

y

1

1, ( x 1).

x 2

x 2

x 2

x 2

f ' x0 0 , то функция f x возрастает в точке x0 ; если f ' x0 0, то

f x

убывает в точке x0 .

Пусть функция f x определена на отрезке a,b .

Если для любых x1, x2 a,b из условия x1

x2 следует неравенство

1)

f x1 f x2 , то функция

f x

-

неубывающая на a,b ;

2)

f x1 f x2 , то функция

f x

-

возрастающая на a,b ;

3)

f x1 f x2 , то функция

f x

-

невозрастающая на a,b ;

4)

f x1 f x2 , то функция

f x

-

убывающая на a,b .

2.3. Необходимые условия экстремума

Теорема. Функция

f x

может иметь экстремум только в тех точках,

в кото-

рых ее производная

f ' x

либо равна нулю, либо не существует.

Доказательство. Пусть

в точке

x0

функция f x имеет производную и

f ' x0 0 . Пусть для определенности

f ' x0 0 . Тогда функция f x

в точке

x0 будет возрастающей. Поэтому найдется такое 0, что для всех x

из ин-

тервала x0

, x0

верно неравенство

f x f x0 ,

а для всех

x из интервала x0 , x0

верно нера-

венство f x f x0 . (см. рисунок).

Из этого следует, что не существует окрестности

точки x0 ,

в которой величина

f x0

была бы наи-

большим

или

наименьшим

значением функции

f x , и поэтому точка x0

не будет ни точкой максимума, ни точкой минимума

функции f x .

Аналогичными рассуждениями придем к тому

же выводу при

f ' x0 0.

Итак, если

в

точке x0

существует производная

f ' x0 0 , то в точке x0 не может быть ни максиму-

ма, ни минимума

функции

f x .

Следовательно,

не имеет: f 0 0 , для x 0

f x 0 , для x 0

f x 0, так что в точке x 0 данная функция воз-

растает.

1

xsin

, x 0,

Для функции f (x)

x

в точке x 0

0, x 0

производная не существует, однако экстремум от-

сутствует.

2.4. Достаточные условия экстремума

Теорема. Пусть x x0 есть критическая точка для функции

f x ,

то есть либо

f ' x0 0 либо f ' x0

не существует, но сама функция

f x непрерывна в

точке x0 .

Пусть существует такое 0, что для всех x из интервала x0

, x0 про-

изводная f ' x 0 , а для всех x из интервала

x0 , x0

имеем

f ' x 0, то

есть при переходе x через точку x0 производная f ' x

меняет знак с плюса на

минус. Тогда в точке x0

функция f x

имеет максимум.

Доказательство. Так как по условию

f ' x 0

в интервале x0 , x0 , то на

отрезке x0 , x0 функция

f x возрастает;

так как

f ' x 0

в интервале

x0 , x0 , то на отрезке x0 , x0

функция f x

убывает. Следовательно,

f x0 есть наибольшее зна-

чение функции

f x в

окрестности x0 , x0

точки x0 , а это означает, что f x0

есть локальный

максимум функции f x .

Теорема.

Пусть

x x0

есть критическая точка для

функции

f x ,

то есть либо f ' x0 0 либо f ' x0 не существует, но сама

функция

f x непрерывна в точке x0 .

x0 , x0

Пусть существует такое 0 ,

что для всех x из интервала

производная f ' x 0, а для всех x

из интервала x0 , x0

имеем

f ' x 0 ,

то есть при переходе x через точку x0 производная f ' x

меняет знак с минуса

на плюс. Тогда в точке x0 функция f x имеет минимум.

1)

найти производную f ' x , приравнять ее к нулю и решить полученное

уравнение f ' x 0;

2)

найти точки, в которых производная f ' x не существует;

(эти точки и корни уравнения

f ' x 0 будут критическими точками

для функции f x );

f ' x слева и справа от каждой критиче-

3)

исследовать знак производной

ской точки.

производная f ' x ме-

Если при переходе x через критическую точку x0

няет знак с плюса на минус, то в точке x0 функция f x

имеет максимум; если

знак f ' x меняется с минуса на плюс, то в точке x0 функция

f x имеет ми-

нимум. Если при переходе x через критическую точку x0 знак

f ' x не меня-

f x0 x

f x0

f x0 x

Экстремум

0

0, ,

0

нет

0

0, ,

0

max

0

0, ,

0

min

0

0, ,

0

нет

Теорема. Пусть в точке

x0

функция

f x

имеет первую и вторую производ-

ные, причем f ' x0 0 ,

а f '' x0 0 .

Тогда в точке x0 данная функция

f x

имеет максимум, если f '' x0 0, и минимум,

если f '' x0 0 .

Доказательство. Точка x0

является критической точкой для данной функции

f x ,

так как f ' x0 0 . Пусть f '' x0 0. Из этого следует, что в точке x0

первая

производная

f ' x

убывает, то есть существует такая окрестность

x0 , x0

точки

f x ,

что для всех x из интервала x0

, x0

верно нера-

венство

f ' x f ' x0 0 ,

а для

всех

x

из

интервала

x0 , x0

верно

f ' x f ' x0 0 .

Таким образом,

при переходе

x через критическую точку

f x производная

f ' x меняет свой знак с плюса на минус. Следовательно,

функция

f x в точке f x имеет максимум.

f x вторая производная

f '' x0 0 , то функция

f x в точке x0 имеет мини-

мум.

f x0

f x0

Экстремум

0

0

max

0

0

min

Пусть кривая задана уравнением y f x и

пусть функция f x в

точке М0 x0 , f x0

имеет

конечную производную

f ' x0 , то есть в

точке

М0 x0 , f x0

существует касательная к данной кри-

вой, не параллельная оси Oy .

Определение.

Если

существует такая окрестность

x0 , x0

точки

М0 x0 , f x0 , что все точки

тельную вторую производную

f '' x 0 , то график функции в этом интервале

выпуклый вверх. Если

f '' x 0

- график выпуклый вниз.

Определение. Точка М0 x0 , f x0

называется

точкой перегиба кривой y f x , если: 1) в точке

x0 существует касательная;

2) существует такая окрестность x0 , x0 точ-

ки х0 , что для x x0 из этой окрестности выпук-

лость кривой направлена в одну сторону, а при

x x0 - в противоположную (см. рисунок).

Теорема. Точка М0 x0 ,

f x0

может быть точкой перегиба кривой

y f x

только если f '' x0 0 (или f '' x0

не существует).

f x x4

Это условие не является достаточным. Так, например, для функции

имеем

f '' x 12x2 и f '' 0 0 , но точка O 0,0 не является точкой перегиба

кривой

y x4 : в этой точке выпуклость кривой на-

правлена вниз.

Теорема. Пусть функция f x

имеет вторую про-

изводную в некоторой окрестности точки x0 , не-

прерывную в точке x0 . Если f '' x0 0 и при пере-

ходе x через точку x0

вторая производная f '' x

меняет знак, то точка М0 x0 , f x0

есть точка пе-

региба кривой y f x .

x0 , f x0 касательную,

Обобщение. Пусть кривая y f x

имеет в точке М0

хотя бы и параллельную оси Oy . Пусть функция f x

в некоторой окрестности

де через точку x0 производная

f '' x меняет свой знак, то точка М0 x0 , f x0

является точкой перегиба кривой y f x .

f x0 x

f x

f x0

f x0

f x

Пере

гиб

0

вып.

0,

0

вып.

нет

вниз

не сущ.

вниз

0

вып.

0,

0

вып.

есть

вниз

не сущ.

вверх

0

вып.

0,

0

вып.

есть

вверх

не сущ.

вниз

0

вып.

0,

0

вып.

нет

вверх

не сущ.

вверх

3.4. Примеры исследования функций

ПРИМЕР. Построить график функции y xe 4 x .

1). x - , , х0

0;

y0

0- точка пересечения с осями.

2). Функция общего вида.

3). f (x) – непрерывна всюду вертикальных асимптот нет.

k

lim

x

0

b lim

x

0

k

lim

x

2

1

x e4 x x

1

x e4 x

x e4x x

y 0

- горизонтальная асимптота при х .

4) y e-4x 4xe 4 x e 4 x 1 4x

, y 0 x

1

.

1

4

1

y -4e-4x 4e 4 x 16xe 4 x

e 4 x (16x 8) , y 0

x 2

.

2

х

1

1

1 1

1

1

;

;

;

4

2

2

4

4 2

у

1

1

4e

2e2

y

+

0

–

–

–

y

–

–

–

0

+

max

перегиб

k lim

f x

lim

x2

1

;

x

x

x 2 x 1 2

2

x3

1

1

2x2 x

b lim

x

lim

1.

2 x 1

2

x 1

2

x

2

2

x

y

1

x 1 является наклонной асимптотой.

2

x2 ( x 3)

4). Находим производную: y

. Знак производной определяется

2( x

3

1)

знаком дроби

x 3

.

Легко получить,

что при x 3 и

x 1

y 0 , а при

x 1

3 x 1

y 0 . Интервалами возрастания являются ; 3

и 1; ; ин-

ствует всюду и обращается в нуль при

x 3

и x 0 .

При x 3

y 0 ,

а при

x 3

y 0 .

Следовательно, точка x 3 является

точкой

максимума.

Находим

значение

функции

при

x 3:

y 3

3

3

27

3,375. При переходе через

другую критическую точ-

8

8

ку x 0 производная знак не меняет, т.е.

x 0 не является точкой экстремума.

5). Находим вторую производную

y

3x

. Видим, что

y 0 при

4

интервал ; 1

( x 1)

x 1,

является областью выпуклости. y 0

при 1 x 0

- это тоже область выпуклости; y 0 при x 0 - это область вогнутости.

В области определения функции

y существует всюду; y 0

при x 0 .

Так как при переходе через эту точку y меняет знак, то

x 0

есть абсцисса

точки перегиба. Находим y( 0 ) 0.

х

; 3

3

3; 1

1

1; 0

0

0;

у

27

0

8

y

+

0

–

+

0

+

y

–

–

–

–

0

+

max

перегиб

График y

x3

имеет вид

2 (x 1)2

ПРИМЕР. Исследовать функцию y

x3

и построить её график.

x2 1

Функция определена всюду, кроме точек x 1.

x3

Точка пересечения графика с координатными осями из

0 имеет коорди-

x2

наты x 0 y 0.

1

1).

Функция нечетная, f x f x ,

график симметричен относительно

начала координат, достаточно исследовать функцию при x 0 .

2).

Точка x 1 является точкой разрыва 2-го рода, график функции имеет

вертикальную асимптоту x 1, lim f x , lim f x .

x 1 0

x 1 0

k lim

f x

x2

x3

x

y x явля-

lim

1;

b lim

x

lim

0 , т.е.

2

1

2

1

2

1

x x

x x

x x

x x

y

x2 x2 3

3). Находим производную:

x2 1 2 . Знак производной определяется

знаком x2 3. При x

3

y 0 ,

а при 0 x 1

и 1 x

3

y 0 . Интервал

возрастания -

; ; интервалы убывания - 0;1

и 1;

. В области опреде-

3

3

ления функции производная обращается в нуль при x 0

и x

.

3

При x

y 0 , а при x

y 0 . Следовательно,

точка

x

является

3

3

3

3

3

3

3

точкой минимума. Находим значение функции при x

3 :

y

3

.

2

2