1 Билет

Понятие матрицы

Основные понятия и обозначения. Пусть m и n два произвольных натуральных числа. Матрицей размера m на n (записывается так )называется совокупность mn вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки. При этом сами числа называютсяэлементами матрицы и каждому элементу ставится в соответствие два числа - номер строки и номер столбца.

Для обозначения матрицы используются прописные латинские буквы, при этом саму матрицу заключают в круглые или прямоугольные или в двойные прямые скобки. Элементы матрицы обозначают строчными латинскими буквами, снабженными двумя индексами: - элемент матрицы, расположенный вi-й строке и j-м столбце или коротко элемент в позиции (i,j). В общем виде матрица размера m на n может быть записана следующим образом

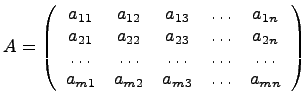
Приведём некоторые обозначения, которыми будем пользоваться в дальнейшем:

- множество всех матриц размера m на n;

- матрица A с элементами в позиции(i,j);

- матрица размера m на n.

Элементы , гдеi=j, называются диагональными, а элементы , где- внедиагональными. Совокупность диагональных элементов, гдеk = min (m,n), называется главной диагональю матрицы.

Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается символом O.

Заметим, что для каждого размера существует своя нулевая матрица.

Матрица размера n на n называется квадратной матрицей n-го порядка, т.е. число строк равно числу столбцов.

Квадратная матрица называется диагональной, если все ее внедиагональные элементы равны нулю.

Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной матрицей и обозначается символом I или E.

Матрица размера называется матрицей-строкой или вектор-строкой. Матрица размераназывается матрицей столбцом или вектор-столбцом.

2 билет

Действия над матрицами

1. Суммой двух матриц является матрица, каждый элемент которой равен сумме соответствующих элементов данных матриц. Складывать можно только матрица одинаковой размерности.

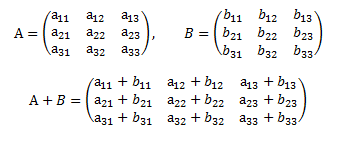
Сложение матриц подчиняется переместительному и сочетательному закону.

2. Умножение матрицы на число 

Чтобы умножить матрицу на число следует каждый элемент матрицы умножить на это число.

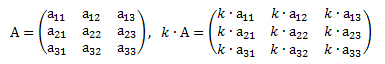
3. Перемножение матриц 

Элемент матрицы-произведения, находящегося на пересечении i-ой строки и j – столбца представляет собой сумму парных произведений элементов i- строки первой матрицы на элементы j – столбца второй матрицы.

Матрицы перемножаются только в том случае, если количество столбцов первой матрицы равно количеству  строк второй матрицы.

Подробнее о перемножении матриц смотрите в видео уроке.  

Разностью матрициодного и того же размера называется матрицатакого же размера, получаемая из исходных путем прибавления к матрицематрицы, умноженной на (-1).

3 билет

Линейные операции:Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен bij = λaij Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен cij = aij + bij Сложение и вычитание допускается только для матриц одинакового размера. Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть A + Θ = A Все элементы нулевой матрицы равны нулю.

Элементарные преобразования матрицы— это такие преобразованияматрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решенийсистемы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарные преобразования используются в методе Гауссадля приведения матрицы ктреугольномуили ступенчатому виду.

Эквивалентные матрицыЭквивалентные матрицы – матрицы, которые могут быть получены одна из другой с помощью элементарных преобразований, а именно: 1) перестановкой местами двух строк матрицы; 2) умножением всех элементов строки на число, отличное от нуля; 3) сложением двух строк.

4 билет

Определи́тель(илидетермина́нт) — одно из основных понятийлинейной алгебры. Определительматрицыявляетсямногочленомот элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случаематрицаможет быть определена над любым коммутативнымкольцом, в этом случае определитель будет элементом того же кольца.

Определитель матрицыАобозначается как:det(A),|А|илиΔ(A).

Минорk-го порядка матрицы(отлат.minor– меньший) – определитель матрицы, составленный из элементов данной матрицы, стоящих на пересечении произвольно выделенных ееkстрок иkстолбцов с сохранением их порядка, т.е.минорk-го порядка есть определитель квадратной матрицы размераk x k.

Каждая n x mматрица имеетминоровk-го порядка. Минорами 1-го порядка являются элементы матрицы. Если номера строк, в которых расположенминор, совпадают с номерами столбцов, то он называетсяглавным минором.

Базисный минор матрицы– отличный от нуляминорk-го порядка этой матрицы такой, что все содержащие егоминоры(k+1)-го порядка равны нулю, или же минор(k+1)-го порядка не существует. Порядок любого базисногоминораматрицы совпадает срангом матрицы, причем каждый столбец (строка) матрицы есть линейная комбинация линейно независимых столбцов (строк), в которых расположенбазисный минор.

В квадратной матрице n-го порядкадополнительным миноромк миноруk-го порядка называется определитель(n-k)-го порядка, полученный из данной матрицы вычеркиванием техkстолбцов и строк, в которых расположен минорk-го порядка.

Алгебраическое дополнение АЛГЕБРАИЧЕСКОЕ ДОПОЛНЕНИЕ[co-factor] — понятиематричной алгебры; применительно кэлементу aij квадратной матрицы Аобразуется путем умноженияминораэлементаaijна (–1)i+j(обозначаетсяАij): Aij= (–1)i+j Mij, где Mij—минорэлементаaijматрицыA=[aij], т. е.определительматрицы, полученной из матрицыAвычеркиваниемстрокиистолбца, на пересечении которых стоит элементaij.Понятие А. д. используется, в частности, в операцииобращения матрицы.

5 билет