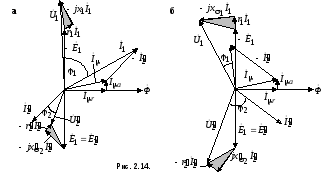
2. Векторные диаграммы трансформаторов при различных вида нагрузки

Векторные диаграммы при нагрузке строят по уравнениям (2.16). Вид векторной диаграммы зависит от характера нагрузки (рис. 2.14).

Векторная диаграмма а рис. 2.14 соответствует активно-индуктивной нагрузке, а векторная диаграмма б - активно-емкостной нагрузке.

Сопоставляя обе диаграммы, можно заключить, что при иувеличение активно-индуктивной нагрузки вызывает снижение напряжения, а при увеличении активно-емкостной нагрузки напряжениевозрастает. Это объясняется тем, что при активно-индуктивной нагрузке происходит некоторое размагничивание трансформатора (потокФ уменьшается, так как ток имеет составляющую, направленную навстречу току), а при активно-емкостной нагрузке трансформатор дополнительно намагничивается (потокФ возрастает, так как ток имеет составляющую, совпадающую с).

Для оценки диапазона изменения напряжения вводится величина, представляющая собой арифметическую разность между вторичным напряжением трансформатора при холостом ходе () и при номинальной нагрузке (). Напряжение первичной обмотки принимается постоянным и равным номинальному.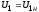

. (2.18)

Для расчета примем допущение, тогда, используя

упрощенную схему замещения (рис.2.15), получим

. (2.19)

Уравнению (2.19) соответствует векторная диаграмма, представленная на рис. 2.16. Из векторной диаграммы следует, что

.

Подставляя приближенное выражение для в уравнение (2.18), получим

.

Отрезок можно выразить через составляющие напряжения короткого замыкания:

,

где .Учитывая, что ,, получим дляпростое выражение

.

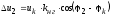На рис. 2.17 представлена зависимость при.

Максимальное снижение напряжения имеет место при , а принапряжение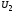не зависит от нагрузки.

2. Определение изменения вторичного напряжения трансформатора и его внешняя характеристика

Изменение напряжения – это арифметическая разность между напряжением номинальным и напряжением при номинальном токе, отнесенная к номинальному напряжению.

Изменением напряжения трансформатора на­зывается арифметическая разность между вторичными напряже­ниями трансформатора при холостом ходе и при номинальном токе нагрузки, когда первичное напряжение постоянно и равно номинальному, а частота также постоянна и равна номинальной.

Изменение напряжения представляет собой важную эксплуата­ционную характеристику трансформатора. Определять изменение напряжения при помощи построения вектор­ной диаграммы неудобно ввиду относительно небольшой его величины и неточности гра­фических построений. Поэтому пользуются аналитической формулой, которая выводится ниже.

Используем для вывода этой формулы уп­рощенную векторную диаграмму (рис. 15-2), построенную в относительных единицах для U\ = U_lH и /_а = /_2н или /₂ = /о,, = /]„ на рис. 15-4. Тогда' падение напряжения и его составляющие будут равны напряжению ко­роткого замыкания и его составляющим в относительных единицах:

Последний член этого выражения обычно относительно мал, и поэтому

Внешняя характеристика

2. Опыт хх

1. Опыт холостого хода

Схема опыта имеет вид, представленный на рис. 2.18.

Опыт проводят для значений напряжения первичной обмотки . Регулирование напряжения осуществляется с помощью индукционного регулятора ИР. Измерительный комплект ИК используется для измерения фазных значений токов, напряжений и активной мощности. По данным измерений строят зависимости тока намагничивания, потерь холостого хода, коэффициента мощностии сопротивления холостого хода,,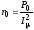в функции напряжения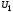. Вид этих зависимостей показан на рис. 2.19. Их называютхарактеристиками холостого хода. Из схемы замещения (рис.2.9) следует, что

;

;

.

В силовых трансформаторах сопротивления ив десятки раз меньше сопротивлений намагничивающего контураи. Поэтому с достаточной степенью точности можно считать, что параметры холостого хода равны параметрам намагничивающей цепи:

; ;.

Это же допущение позволяет считать равными модули ЭДС и напряженияпервичной обмотки и, следовательно, приближенно определить коэффициент трансформации

.

Ток холостого хода в силовых трансформаторах лежит в пределах, поэтому электрические потери в первичной обмоткеневелики, и все потери холостого хода можно полагать равными потерям в стали. Потери в стали, как отмечалось выше, пропорциональны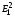, а на холостом ходу они будут пропорциональны и, поэтому зависимость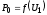имеет параболический характер.Потери холостого хода иток холостого хода , определенные при номинальном напряжении, являются паспортными величинами трансформатора и приводятся в справочниках.

Зависимость являетсяобращенной магнитной характеристикой трансформатора, так как . Нелинейный характер зависимостейиобъясняет и сильную зависимость параметров холостого хода иот напряжения.

Соответствие тока намагничивания , потерь холостого хода, коэффициента мощностии параметровирасчетным данным проверяется для номинального напряжения.

2. Режим холостого хода

В режиме холостого хода первичная обмотка трансформатора включена в сеть на напряжение , а вторичная разомкнута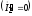. Для этого режима справедливы уравнения

(2.17)

Ток первичной обмотки представляет собой намагничивающий ток трансформатора. Построение векторной диаграммы (рис.2.10) начинают с вектора потока . ЭДСиотстают от потока на угол 90. Реактивная составляющая тока намагничивания совпадает по фазе с потоком, а его активная составляющая опережает поток на 90. Намагничивающий ток несколько опережает поток. Для получения вектора первичного напряжения необходимо построить вектори прибавить к нему падения напряжений на активноми индуктивном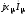сопротивлениях. Из векторной диаграммы видно, чтоочень мал. Обычно. Трансформатор потребляет из сети реактивную мощность на создание магнитного поля в трансформаторе.