
- •Уравнения трансформатора
- •Т-образная схема замещения трансформатора
- •Векторные диаграммы трансформаторов при различных вида нагрузки
- •Определение изменения вторичного напряжения трансформатора и его внешняя характеристика
- •Опыт хх
- •Опыт кз
- •Определение потерь и кпд трансформатора
- •Параллельная работа трансформатора при неодинаковых коэффициентах трансформации
- •Параллельная работа трансформатора при неодинаковых напряжениях кз
Принцип действия трансформатора. Основные элементы конструкции.


Уравнение напряжений и мдс приведенного трансформатора
Реальное магнитное
поле трансформатора имеет довольно
сложный характер. С целью упрощения
анализа магнитное поле разделяют на
поле взаимной
индукции,
трубки которого замыкаются по стальному
сердечнику и образуют поток Ф,
и поле
рассеяния,
которое обусловливает потоки
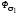 и
и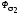 ,
каждый из которых сцеплен только со
своей обмоткой (рис.2.5). Магнитное поле
взаимной индукции можно рассчитать с
помощью закона полного тока. Для любого
контура, полностью замыкающегося по
стальному сердечнику, имеем
,
каждый из которых сцеплен только со
своей обмоткой (рис.2.5). Магнитное поле
взаимной индукции можно рассчитать с
помощью закона полного тока. Для любого
контура, полностью замыкающегося по
стальному сердечнику, имеем
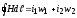 .
.
Уравнение упрощается,
если принять допущение о равномерности
магнитного поля по сечению магнитопровода
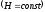 :
:
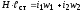 .
.
Введем обозначения:
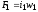 - МДС первичной обмотки;
- МДС первичной обмотки;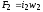 - МДС вторичной обмотки;
- МДС вторичной обмотки;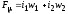 - результирующая МДС. И учитывая, что
- результирующая МДС. И учитывая, что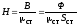 ,
получим
,
получим
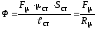 ,
(2.4)
,
(2.4)
где
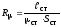 - магнитное сопротивление;
- магнитное сопротивление;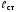 и
и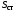 - длина и площадь поперечного сечения
магнитопровода
- длина и площадь поперечного сечения
магнитопровода
Выражение (2.4) можно трактовать как закон Ома для магнитной цепи: МДС аналогична ЭДС, поток - току, магнитное сопротивление - электрическому сопротивлению.
Если выразить
результирующую МДС
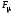 через ток намагничивания
через ток намагничивания ,
,
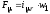 ,
,
то получим уравнение магнитной характеристики трансформатора без учета потерь
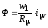 . (2.5)
. (2.5)
Поток Ф
образует с первичной обмоткой
потокосцепление
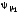 ,
а со вторичной -
,
а со вторичной -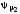 ;
;
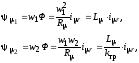
где
 - взаимная индуктивность первичной
обмотки;
- взаимная индуктивность первичной
обмотки;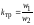 - коэффициент трансформации.
- коэффициент трансформации.
Магнитные поля рассеяния образуют потокосцепления рассеяния соответствующих обмоток:
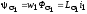 ;
;
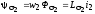 ,
,
где
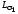 и
и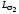 - индуктивности рассеяния первичной и
вторичной обмоток соответственно.
- индуктивности рассеяния первичной и
вторичной обмоток соответственно.
Индуктивности
рассеяния обмоток трансформатора
значительно меньше взаимной индуктивности
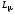 ,
так как определяются потоками рассеяния,
замыкающимися, главным образом, по
немагнитным участкам (рис. 2.5). По этой
же причине индуктивности
,
так как определяются потоками рассеяния,
замыкающимися, главным образом, по
немагнитным участкам (рис. 2.5). По этой
же причине индуктивности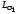 и
и можно принять постоянными, в то время
как взаимная индуктивность
можно принять постоянными, в то время
как взаимная индуктивность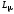 зависит от степени насыщения стали
зависит от степени насыщения стали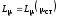 .
.
Уравнения трансформатора
Зная картину магнитного поля в трансформаторе, можно определить ЭДС, действующие в обмотках:
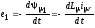 - ЭДС первичной обмотки от поля
взаимоиндукции;
- ЭДС первичной обмотки от поля
взаимоиндукции;
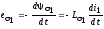 - ЭДС первичной обмотки от поля рассеяния;
- ЭДС первичной обмотки от поля рассеяния;
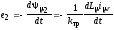 - ЭДС вторичной
обмотки от поля взаимоиндукции;
- ЭДС вторичной
обмотки от поля взаимоиндукции;
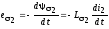 - ЭДС вторичной обмотки от поля рассеяния.
- ЭДС вторичной обмотки от поля рассеяния.
Уравнения трансформатора представляют собой баланс напряжений и ЭДС, действующих в каждой обмотке:
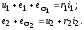 (2.6)
(2.6)
Здесь напряжение
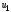 рассматривается как ЭДС источника
питания, а
рассматривается как ЭДС источника
питания, а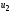 - как падение напряжения на нагрузке.
- как падение напряжения на нагрузке.
Решая систему (2.6) относительно напряжений, получим
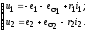 (2.7)
(2.7)
Используя полученные
выше выражения для ЭДС и принимая
допущение
 ,
представим уравнение (2.7) в виде линейной
системы дифференциальных уравнений:
,
представим уравнение (2.7) в виде линейной
системы дифференциальных уравнений:
 (2.8)
(2.8)
Реактивная
составляющая тока намагничивания
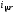 определяется из уравнения для
результирующей МДС:
определяется из уравнения для
результирующей МДС:
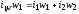 ,
,
отсюда
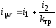 .
.
Для уравнений трансформатора может быть предложена векторная диаграмма, являющаяся геометрической интерпретацией уравнений трансформатора на комплексной плбскости. '.
Так как коэффициент трансформаций может достигать нескольких десятков, строить диаграмму с векторами первичной и вторичной обмоток, отличающимися в несколько десятков раз, неудобно. Поэтому принято векторную диаграмму и схему замещения рассматривать для приведенного трансформатора.
В приведенном трансформаторе числа витков первичной и вторичной обмоток одни и те же (ац = w2). При этом все электромагнитные процессы в реальном и приведенном трансформаторах протекают одинаково. В реальном н приведенном трансформаторах остаются неизменными потери, МДС, магнитные потоки, активные и реактивные мощности. Если определять коэффициент трансформации как отношение витков первичной обмотки к виткам вторичной (2.6), то можно для приведенного и реального трансформаторов составить следующие соотношения:

Чтобы магнитные поля в реальном и приведенном трансформаторах оставались неизменными, должны выполняться равенство (2.24) и сохраняться конфигурация обмоток. При этом сечения приведенной и реальной
обмоток должны быть одинаковыми, поэтому сечение витка приведенной обмотки изменяется в п12 раз.
Активное
сопротивление приведенной обмотки в
п]г
раз больше, чем активное сопротивление
реальной обмотки, из-за изменения в п12
раз числа витков и сечения витка:
![]() (2.25)
(2.25)
Так
как при неизменных геометрических
размерах индуктивные сопротивления
зависят от квадрата числа витков![]() (2.26)
(2.26)
то
при этом![]() (2.27)
(2.27)
Эти соотношения могут быть получены и из равенства активных и реактивных мощностей трансформаторов.
Для трансформатора с приведенными обмотками уравнения выглядят следующим образом:
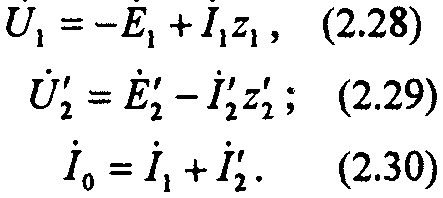
Геометрической интерпретацией (2.28)—(2.30) является векторная диаграмма приведенного трансформатора (рис. 2.4, а).
Построение диаграммы лучше начать с уравнения (2.30), отложив поток в фазе Ф„, а затем строить (2.28) и (2.29).
Мощность,
подводимая к первичной обмотке
трансформатора (рис. 2.4, а),
![]()
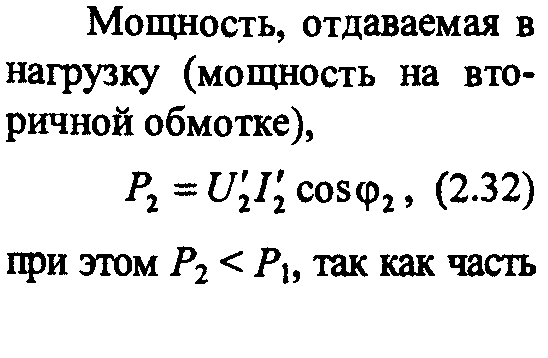 мощности
расходуется на потери Р2
в трансформаторе.
мощности
расходуется на потери Р2
в трансформаторе.
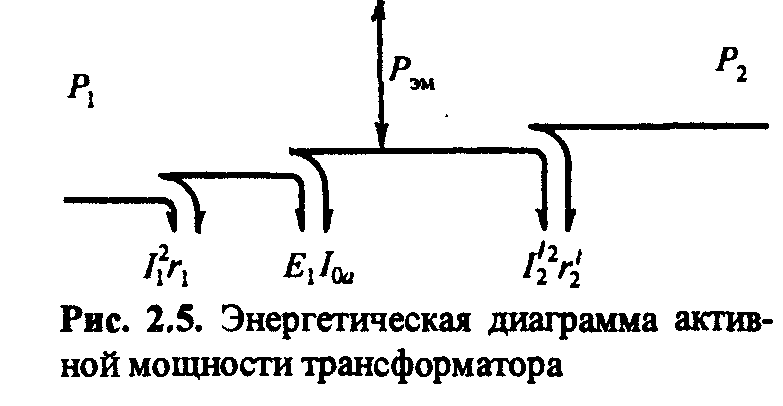
На рис. 2.5 дана энергетическая диаграмма активной мощности в трансформаторе. Часть активной мощности расходуется
Рис. 2.5. Энергетическая диаграмма актив- на потери в меди первичной /,2 г,
ной
мощности трансформатора
Если нагрузка трансформатора индуктивная, реактивная мощность от трансформатора поступает в нагрузку. Если нагрузка трансформатора емкостная и активная, то при большой емкости реактивная мощность поступает в трансформатор и в сеть. При этом Р2р > Р 1р- Направления активной и реактивной мощностей могут совпадать или быть встречными.
Как следует из векторной диаграммы трансформатора, при смешанной емкостной нагрузке JJ\ > Ui (рис. 2.4, б). При чисто емкостной нагрузке возрастание напряжения на вторичной обмотке может быть столь значительным, что это окажется опасным для изоляции. Возрастание напряжения на трансформаторе при емкостной нагрузке называется перевозбуждением трансформатора.
