Контрольные вопросы

1. Как построить полярный и декартовый графики?

2. Как построить несколько графиков в одной системе координат?

3. Как изменить масштаб графика?

4. Как определить координату точки на графике?

5. Как построить гистограмму?

6. Как создать анимацию в MathCad?

7. Какие средства имеются для управления отображением линий на графике?

6. Решение уравнений

6.1. Решение алгебраического уравнения

Д

Рис. 16. Решение алгебраического уравнения

ля поиска корней обычного полинома степени n видаa_nxⁿ +...+ a₂x² + a₁x + a₀ удобно использовать функцию polyroots(A). Эта функция не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные.Коэффициенты полинома находятся в векторе, содержащем n+1 элементов. Результат представляется вектором длины n, состоящим из корней полинома.

Не рекомендуется использовать эту функцию, если степень полинома выше пятой, поскольку возрастает погрешность вычисления.

На рис. 16 приведен пример поиска корней полинома с помощью функции polyroots.

6.2. Решение трансцендентного уравнения

Трансцендентные уравнения, как правило, не имеют аналитического решения. Они решаются численными методами с заданной погрешностью, которая определяется системной переменной TOL. Для решения одного уравнения с одним неизвестным используется функция root(f(x), x).Аргументами этой функции являются выражение и переменная, входящая в выражение. Функция возвращает значение переменной, которое обращает выражение в ноль.

Решение выполняется в следующей последовательности. Вначале определяется выражение, которое должно быть обращено в ноль. На рис. 17 это функция p(x). Затем строится график функции для определения числа корней уравнения. В примере (рис. 17) из графика следует, что задача сводится к отысканию трех корней.

П

Рис. 17. Решение трансцендентного уравнения

еред использованием функции root переменной x присваивается числовое значение − начальное значение. Присвоенное переменной x начальное значение становится первым приближением к искомому корню. Далее подключается функция root для определения значения первого корня, записываемого в переменную x1.

Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат. Результат можно увидеть, напечатав x1=.

Предлагаемая схема повторяется для остальных корней x2, x3 (рис. 17).

Часто нужно решать уравнение многократно при изменении одного из параметров этого уравнения. Самый простой способ состоит в определении функцииf(a, x).

Чтобы решить уравнение для конкретного значения параметра a, необходимо присвоить параметру a интервал исследуемых значений и начальное значение переменной x как аргументам этой функции. Затем определить правило нахождения искомого значения корня: x_a:= f(a,x).

Н

Рис. 18. Решение уравнения с параметром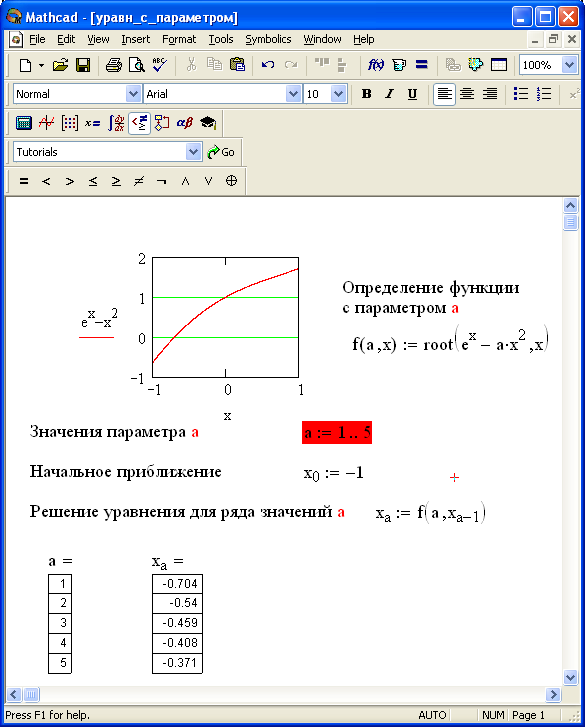

апример, пусть требуется решить уравнениеexp(x) = a*x² для различных значений параметра а.

С помощью графика для одного из значений параметра a нужно определить число корней. В нашем случае имеется один корень (рис. 18).

Далее поступить с вышеописанной схемой. В конце решения задачи вывести значения корней x_a для каждого параметра a (рис. 18).

Р

Рис. 19. Использование оператора Solve

ешение уравненияexp(x) = a*x² в символьном виде можно получить с помощью оператора Solve. При его вызове появляется шаблон с двумя маркерами для ввода (рис. 19). Решение выдается после выхода из зоны оператора автоматически.

Оператор Solve используется также для решения неравенств. Порядок применения тот же, что и при решении уравнений (рис. 19).