
- •Точки перегиба
- •Общая схема исследования функции и построения графика
- •Типы задач
- •1. Возрастание и убывание функций
- •2. Экстремумы функции
- •3. Асимптоты графика функции
- •4. Построение графиков функций
- •5. Определение скорости возрастания и убывания функций
- •6. Доказательство неравенств с помощью производной
- •7. Применение производной в теории многочленов для нахождения интервала залегания корней и определения их количества. Связь многочлена со своей производной
- •8. Нахождение наибольшего и наименьшего значения непрерывной функции на отрезке
- •9. Текстовые задачи разного содержания на нахождение наибольшего и наименьшего значения величин
- •II. Кривые, заданные параметрически
- •III. Векторные функции действительной переменной
- •IV. Комплексные функции действительной переменной
4. Построение графиков функций
|
№ п/п |
Пример ПП 16 4. Построение графиков функций |
|
№19 |
Исследуйте
функцию
При
вычислении второго предела использовано
правило Лопиталя для раскрытия
неопределённости типа
4 |
5. Определение скорости возрастания и убывания функций
Скорость
роста линейной функции
![]() постоянна и равна
постоянна и равна![]() ,
квадратичной функции – линейна, и
вообще, производная степенной функции,
являясь меньшей степенью, растет
медленнее, чем сама функция; скорость
роста показательной функции пропорциональна
значению самой функции, так как
,
квадратичной функции – линейна, и
вообще, производная степенной функции,
являясь меньшей степенью, растет
медленнее, чем сама функция; скорость
роста показательной функции пропорциональна
значению самой функции, так как![]() .
.
|
№ п/п |
Пример ПП 16 5. Определение скорости возрастания и убывания функций |
|
№20 |
Какая
из функций
При
Определим,
начиная с каких значений аргумента
Рассмотрим
|
6. Доказательство неравенств с помощью производной
Если
в точке
![]() выполняется условие
выполняется условие![]() и для всех
и для всех![]() выполняется условие
выполняется условие![]() ,
то для всех
,
то для всех![]() верно неравенство
верно неравенство![]() .
.
|
№ п/п |
Пример ПП 16 6. Доказательство неравенств с помощью производной
|
|
№21 |
Докажите
неравенство:
Рассмотрим
|

 ,
,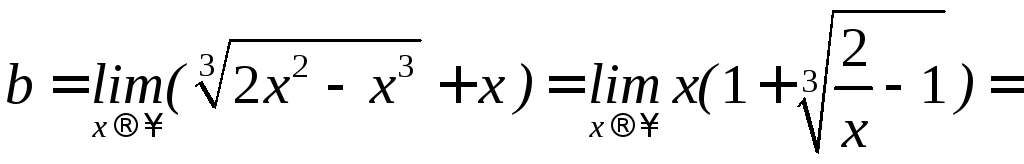

 .
Знак производной определяется знаком
выражения
.
Знак производной определяется знаком
выражения
 .
Видим, что в области
.
Видим, что в области .
При переходе через
.
При переходе через
 )
Находим вторую производную:
)
Находим вторую производную: .
Видим, что
.
Видим, что