ПП 16.

I. ИССЛЕДОВАНИЕ ФУНКЦИЙ и построение графиков

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ

Графики элементарных функций

1. Линейная функция:.

2. Квадратичная функция: .

3. Степенные функции

3.1. . 3.2. ,.

3.3. Иррациональные .

Трансцендентные функции

4. Показательная .

5. Логарифмическая .

6. Тригонометрические функции

6.1. . 6.2.. 6.3.. 6.4..

7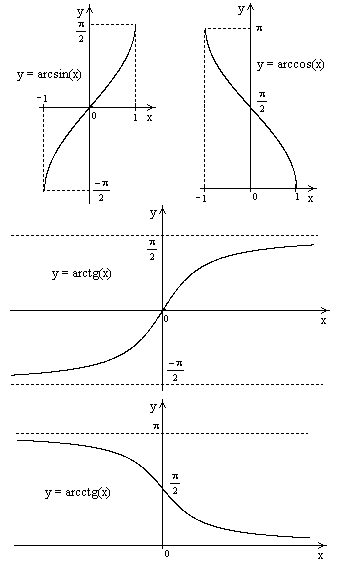. Обратные тригонометрические функции

7.1. ..

7.2. ..

7.3. ,.

7.4. ..

, ,.

8. Гиперболические функции

8.1. Гиперболический синус

.

8.2. Гиперболический косинус

.

8.3. Гиперболический тангенс

.

8.4. Гиперболический котангенс

. ,,,.

Асимптоты

1) - вертикальная асимптота , если .

2) - правая (левая) горизонтальная асимптота , если .

3) ,,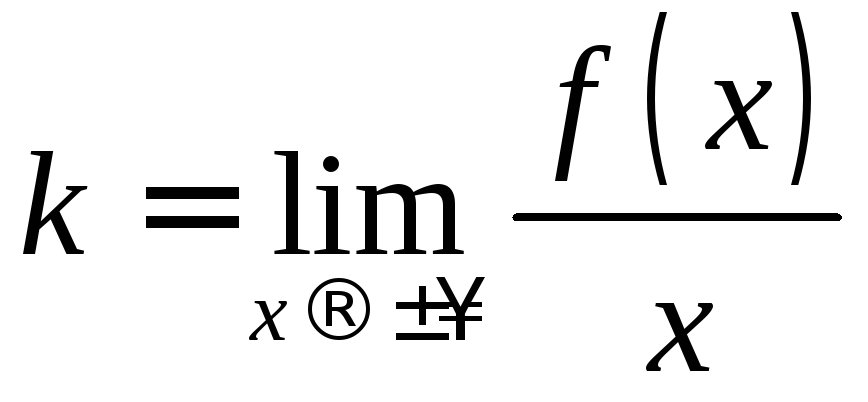- наклонная асимптотапри.

ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНОЙ

Интервалы монотонности

Функция , дифференцируемая на отрезке , возрастает (убывает) тогда и только тогда, когда(),.

Правило отыскания экстремумов функции

Чтобы найти точки максимума и минимума функции , надо:

1). Найти производную , приравнять ее к нулю и решить полученное уравнение .

2). Найти точки, в которых производная не существует.

3). Исследовать знак производной слева и справа от каждой критической точки.

			Экстремум
			нет
			max
			min
			нет

С помощью второй производной:

		Экстремум
0		max
0		min
0	0

Точки перегиба

Функция , дифференцируемая на отрезке,выпукла вниз (вверх) тогда и только тогда, когда (),.

					Перегиб
	вып. вниз			вып. вниз	нет
	вып. вниз			вып. вверх	есть
	вып. вверх			вып. вниз	есть
	вып. вверх			вып. вверх	нет

Общая схема исследования функции и построения графика

1. Найти область определения функции; найти область значений функции; найти точки пересечения графика с осями координат, указать интервалы знакопостоянства функции.

2. Проверить функцию на периодичность; проверить функцию на четность и нечетность.

3. Исследовать функцию на непрерывность, найти точки разрыва функции и ее односторонние пределы в этих точках; определить наличие горизонтальных, вертикальных и наклонных асимптот.

4. Вычислив первую производную, найти критические точки и интервалы монотонности функции, выделить точки локальных экстремумов.

5. Вычислив вторую производную, найти интервалы выпуклости и точки перегиба графика функции.

6. Построить график.

Типы задач

1. Возрастание и убывание функций

Функция, дифференцируемая на интервале,возрастает (убывает) на тогда и только тогда, когда () для всех.

Геометрически это означает, что угол наклона касательной к графику возрастающей (убывающей) дифференцируемой функции острый (тупой), а угловые коэффициенты касательных соответственно положительны или отрицательны.

№ п/п	Примеры ПП 16 1. Возрастание и убывание функций
№1.	По данному графику функциипостройте вид графиков. Решение: 1) На интервале убывает,,. 2) На интервалевозрастает, . 3) На интервале убывает,. 4) . 5) На интервале возрастает,, на интервалеубывает,. Эти соображения позволяют построить примерный график. 6) Та же последовательность действий, примененная к графику функции, дает примерный график второй производной.
№2.	По данному графику производнойпостройте вид графика функции. Решение: 1) На интервале ,возрастает,, т.е., скорость возрастаниятакже неограниченно возрастает, а следовательно, и сама функциянеограниченно возрастает, т.о.,– вертикальная асимптота графика. 2) На интервале ,возрастает, причем, (чем ближе точка к– справа от нее, тем больше скорость возрастания), что указывает, что, т.е.,– точка разрыва второго рода. 3) В точке производная меняет знак с «+» на «–»,– точка локального максимума. 4) На интервале ,убывает. 5) В точке производная меняет знак с «–» на «+»,– точка локального минимума. 6) Прифункция возрастает. Эти соображения позволяют построить примерный график :
№3.	Функция возрастает в своей области определения, так какпри любых.
№4.	Функция возрастает на интервале, так как для. Полезный вывод: поскольку , то, значитдля.