
ПП 17. Комплексные числа.
Многочлены в комплексной области.
КОМПЛЕКСНЫЕ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ
Основные определения и формулы
1.Комплексные числа
1.1. Комплексные числа. Алгебраическая форма комплексного числа
Мнимая единица
![]() .
.
Алгебраической формой комплексного числа называется выражение вида:
![]() .
.
Действительное
число
![]() называется действительной
частью
комплексного числа
называется действительной
частью
комплексного числа
![]() ,
действительное число
,
действительное число
![]() называется мнимой
частью
называется мнимой
частью
![]() .
.
Комплексное
число
![]() ,
если
,
если
![]() и
и
![]() .
.
![]() .
.
1.2. Модуль и аргумент комплексного числа. Тригонометрическая форма комплексного числа
Комплексная плоскость:

Геометрическая
интерпретация комплексного числа
![]() :
точка
:
точка
![]()
на
комплексной плоскости или вектор
![]() .
.
Модуль
комплексного числа:
![]()
Геометрический смысл модуля комплексного числа:
![]() - расстояние от точки
- расстояние от точки
![]() до начала координат;
до начала координат;
![]() - расстояние от точки
- расстояние от точки
![]() до точки
до точки
![]() ;
;
![]() - уравнение окружности с центром в точке
- уравнение окружности с центром в точке
![]() и радиусом R;
и радиусом R;
![]() - геометрическое место точек, равноудаленных
от точек
- геометрическое место точек, равноудаленных
от точек
![]() и
и
![]() .
.
Угол
![]() между радиус-вектором
между радиус-вектором
![]() и
положительным направлением оси OX
называется аргументом комплексного
числа z:
и
положительным направлением оси OX
называется аргументом комплексного
числа z:
![]() ,
,
где
![]() – главное значение аргумента,
– главное значение аргумента,
![]() .
.
Для числа
![]() аргумент не определён.
аргумент не определён.
При этом аргумент комплексного числа определяется следующим образом:


Тригонометрическая форма записи комплексного числа:
![]() ,
,
т.к.
![]() ,
,
![]() .
.
1.3. Формула Эйлера. Показательная форма комплексного числа
Показательная форма комплексного числа:
![]() ,
,
![]() .
.
Получается
из формулы Эйлера:
![]()
(будет доказана позже, при изучении теории рядов).
Свойства
![]() :
:
10.
![]() - периодическая функция;
- периодическая функция;
20.
![]() - значения функции
- значения функции
![]() лежат на окружности
лежат на окружности
![]() ;
;
30.
![]()
1.4. Действия над комплексными числами
![]()
![]() ,
,
![]() .
.
![]()
 ,
если
,
если
![]() и
и
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
С геометрической точки зрения сложение (вычитание) комплексных чисел равносильно сложению (вычитанию) изображающих их векторов.
В алгебраической форме:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
 .
.
В тригонометрической форме:
1)
![]() ;
;
2)
![]() .
.
Действия возведения в степень и извлечения корня удобнее производить над комплексными числами, записанными в тригонометрической или показательной форме:
![]() (формула
Муавра)
(формула
Муавра)
![]() ,
,
где
![]() .
.
Корень n-й степени из комплексного числа имеет n различных значений:
![]() ,
,
![]() ,
,
![]() ,
,
………………………
![]() .
.
Числа
![]() имеют одинаковый модуль, значения корня
будут изображаться точками на одной
окружности.
имеют одинаковый модуль, значения корня
будут изображаться точками на одной
окружности.
В показательной форме:
-
 ;
3)
;
3)
 ;
; -
 ;
4)
;
4) ,
,
 .
.
Формулы Эйлера
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,так
как
,так
как
![]() .
.
Действия сложения и вычитания производятся только в алгебраической форме, действия умножения и деления удобнее выполнять в показательной форме, а тригонометрическая форма используется как переходная от алгебраической к показательной и наоборот.
1.5. Комплексное сопряжение
Комплексные
числа
![]() и
и
![]() называются сопряженными.
называются сопряженными.
В
показательной форме:
![]() ,
,
![]() .
.
Свойства операции сопряжения:
1°. ![]() ;
;
2°. ![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() - действительное число;
- действительное число;
3°. ![]() ,
,
4°. ![]() ,
,
5°. 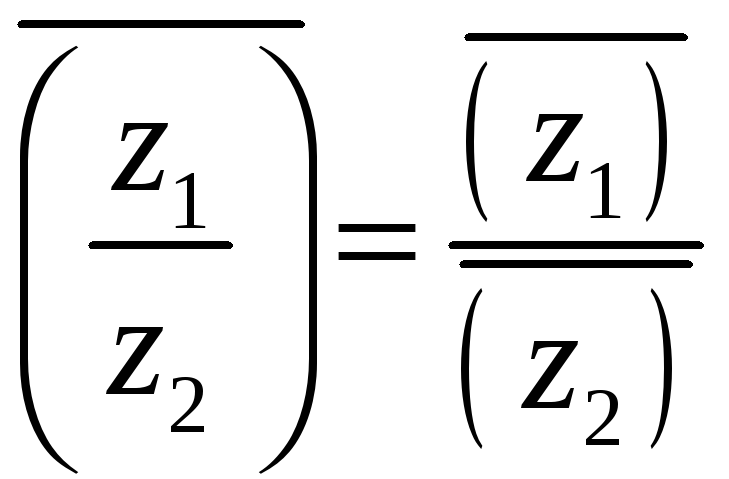 ,
,
6°. ![]() .
.
1.6. Свойства операций сложения и умножения:
1°. ![]() ,
,
2°. ![]() ,
,
3° ![]() ,
,
4°. ![]() ,
,
5°. ![]() .
.
2. Многочлены в комплексной области.
Корни многочлена
Многочлен:
![]() ,
При
,
При
![]() многочлен называется приведённым.
многочлен называется приведённым.
Рациональная дробь:
 .
.
При
![]() дробь называется правильной,
дробь называется правильной,
при
![]() дробь называется неправильной.
дробь называется неправильной.
Неправильную дробь всегда можно разложить на сумму многочлена и правильной дроби:
 .
.
Корнем
многочлена
![]() называют число
называют число
![]() ,
удовлетворяющее уравнению
,
удовлетворяющее уравнению
![]()
Теорема
Безу. Остаток,
получаемый при делении
![]() на
(z-a),
равен
на
(z-a),
равен
![]()
Следствие.
Для того
чтобы многочлен
![]() делился на выражение
делился на выражение
![]() без остатка, необходимо и достаточно,
чтобы число
без остатка, необходимо и достаточно,
чтобы число
![]() было корнем этого многочлена:
было корнем этого многочлена:
![]() .
.
Если
![]() ,
,
![]() - корень
кратности
- корень
кратности
![]() .
.
Основная теорема алгебры многочленов
Любой
многочлен
![]() при
при
![]() имеет хотя бы один корень (действительный
или комплексный).
имеет хотя бы один корень (действительный
или комплексный).
Следствия:
1). Каждый многочлен
![]() имеет ровно
имеет ровно
![]() корней, если каждый корень считать
столько раз, какова его кратность.
корней, если каждый корень считать
столько раз, какова его кратность.
2). Всякий многочлен n-й степени
разлагается на n линейных множителей
вида
![]() и множитель, равный коэффициенту при
и множитель, равный коэффициенту при
![]() :
:
![]() .
Для
случая кратных (повторяющихся) корней
формула принимает вид:
.
Для
случая кратных (повторяющихся) корней
формула принимает вид:
![]() ,
здесь
,
здесь
![]() – корни кратности
– корни кратности
![]() ,
,
![]() ,
,
![]() .
.
Комплексные корни многочлена с действительными коэффициентами появляются сопряженными парами:
если
многочлен
![]() с действительными коэффициентами имеет
комплексный корень
с действительными коэффициентами имеет
комплексный корень
![]() кратности к, то он имеет и комплексно-сопряженный
корень
кратности к, то он имеет и комплексно-сопряженный
корень
![]() той же кратности.
той же кратности.
Многочлен с действительными коэффициентами разлагается на линейные и квадратичные множители с действительными коэффициентами:
![]()
![]() ,
где
,
где
![]() .
.
Линейные
множители
![]() соответствуют
действительным корням
соответствуют
действительным корням
![]() кратности
кратности
![]() ;
квадратичные множители
;
квадратичные множители
![]()
с
действительными коэффициентами p,
q
и отрицательным дискриминантом
![]() соответствуют паре комплексно-сопряженных
корней
соответствуют паре комплексно-сопряженных
корней
![]() кратности
кратности
![]() .
.
