- •Пп 26 однородные и неоднородные дифференциальные уравнения (олду и нлду) с постоянными коэффициентами
- •1. Решение олду второго порядка с постоянными коэффициентами
- •2. Олду n-го порядка с постоянными коэффициентами ,,
- •3.Решение нлду второго порядка с постоянными коэффициентами методом неопределенных коэффициентов
- •Принцип суперпозиции
- •4. Метод вариации произвольных постоянных для решения нлду второго порядка
- •5. Решение нлду n-го порядка с постоянными коэффициентами методом неопределенных коэффициентов,
- •6. Метод вариации произвольных постоянных для нлду высших порядков
Пп 26 однородные и неоднородные дифференциальные уравнения (олду и нлду) с постоянными коэффициентами
1. Решение олду второго порядка с постоянными коэффициентами
|
Корни характеристического уравнения |
Вид общего решения |
|
1.
действительные, разные. |
|
|
2.
действительные, равные, кратность 2. |
|
|
3.
комплексные. |
|
|
4.
|
|
|
№ п/п |
ЗАДАЧИ ПП 26 1.
Решение ОЛДУ второго порядка
|
Ответ |
|
№ 1 |
Найдите
решение ОЛДУ
Решение:
|
|
|
№ 2 |
Найдите
решение ОЛДУ
Решение:
|
|
|
№ 3 |
Найдите
решение ОЛДУ
Решение:
|
|
2. Олду n-го порядка с постоянными коэффициентами ,,
|
Корни характеристического уравнения |
Вклад указанных корней в общее решение ДУ |
|
1. Действительные, разные
|
|
|
2.
Действительные, кратности
|
|
|
3. Комплексные, разные
|
|
|
4.
Комплексные, кратности
|
|
|
№ п/п |
ЗАДАЧИ ПП 26 2. Решение ОЛДУ n-го порядка с постоянными коэффициентами |
Ответ |
|
№ 3 |
Решите
уравнение
Решение:
Характеристическое
уравнение:
Частные решения имеют вид:
Общее
решение имеет вид:
|
|
3.Решение нлду второго порядка с постоянными коэффициентами методом неопределенных коэффициентов
|
|
Корни характеристического уравнения |
Вид
|
|
1.
|
а) 0 – не корень б) 0 – корень кратности r (r =1,2) |
|
|
2.
|
а)
б)
|
|
|
3.
|
а)
б)
|
|
|
4.
|
а)
б)
|
|
|
5.
|
а)
б)
|
|
Здесь Q и M – многочлены с неизвестными коэффициентами.
|
№ п/п |
ЗАДАЧИ ПП 26 3. Решение НЛДУ второго порядка с постоянными коэффициентами методом неопределенных коэффициентов |
Ответ |
|
№ 4 |
Найдите
решение НЛДУ
Решение: 1) Находим общее решение соответствующее однородного уравнения. ОЛДУ
Ищем
решение в виде
Подстановка в уравнение дает характеристическое уравнение для k:
корни
характеристического уравнения
фундаментальная
система решений однородного уравнения
общее
решение однородного уравнения
2)
Находим частное решение
Правая
часть уравнения имеет вид
не
совпадает с корнями характеристического
уравнения
частное
решение ищем в виде
где
А
неизвестный коэффициент,
Подстановка
частное
решение НЛДУ:
3) Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и любого частного решения исходного неоднородного уравнения:
|
|
|
№ 5 |
Решите
ДУ
Решение:
1) ОЛДУ
2)
3)
4)
При
Частное
решение НЛДУ имеет вид:
|
|
|
№ 6 |
Решите
уравнение
Решение:
1)
2)
3)
|
|
|
№ 7 |
Найдите
решение НЛДУ
Решение:
1)
2)
Подстановка в уравнение дает:
откуда
3)
|
|
|
№ 8 |
Найдите общее решение дифференциального уравнения
Решение: НЛДУ - 3-го порядка с постоянными коэффициентами. 1)
2)
Правая часть уравнения имеет вид
Для
определения неизвестных коэффициентов
А, В, С
подставляем решение
в исходное уравнение:
Группируем
члены в левой части по степеням х: Приравняем коэффициенты при одинаковых степенях х:
Частное решение неоднородного уравнения имеет вид 3) Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и любого частного решения исходного неоднородного уравнения
|
|
|
№ 9 |
Найдите общее решение дифференциального уравнения
Решение:
1)
Находим общее решение однородного
уравнения.
Общее решение однородного уравнения:
2) Находим частное решение неоднородного уравнения.
Поскольку
характеристическое число для правой
части
Подставим
эти выражения в исходное уравнение: Приравнивая коэффициенты при одинаковых степенях х, найдем систему линейных уравнений для нахождения неопределенных коэффициентов:
Частное
решение неоднородного уравнения имеет
вид
3) Общее решение исходного неоднородного уравнения:
|
|
|
№ 10 |
Найдите общее решение дифференциального уравнения Решение: 1) Находим общее решение неоднородного уравнения.
2)
Находим частное решение
Правая
часть уравнения: Характеристическое
число для правой части является
комплексным,
Частное решение ищем в виде: Подставим
в уравнение функцию
Приравняем
коэффициенты при
Частное решение : 3)
Общее решение неоднородного уравнения:
|
|

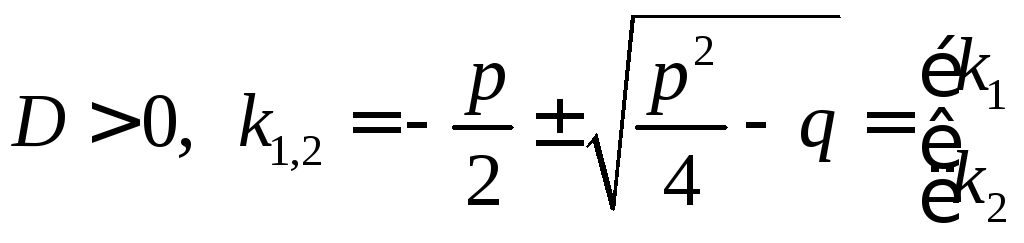 -
-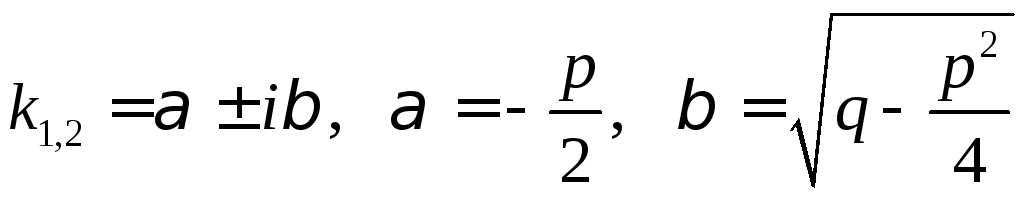 -
-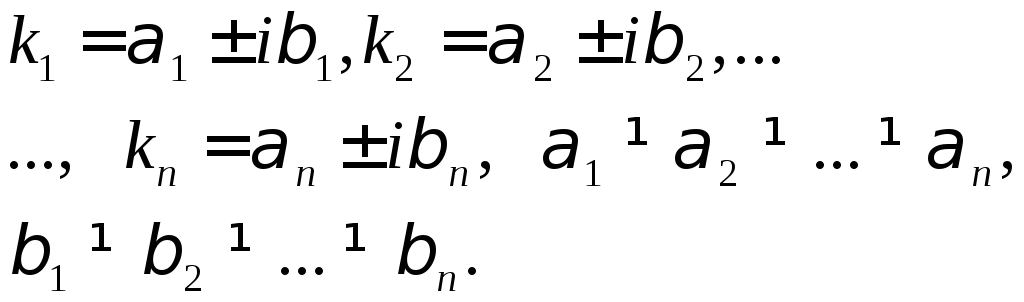
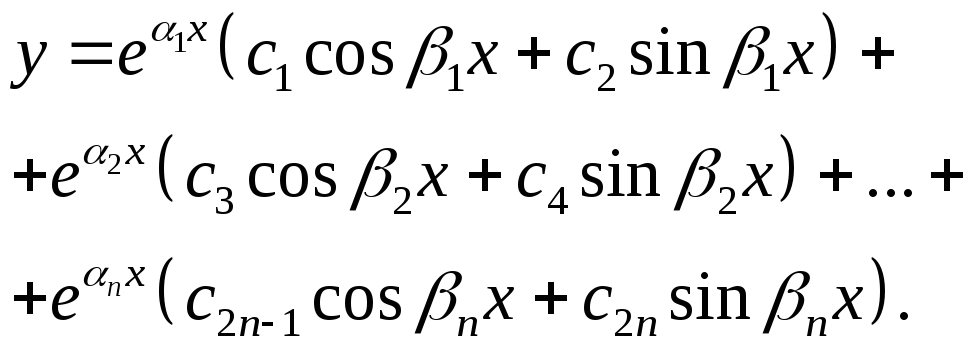
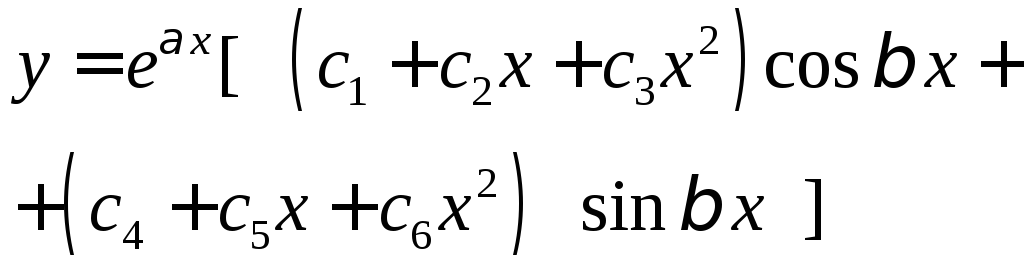
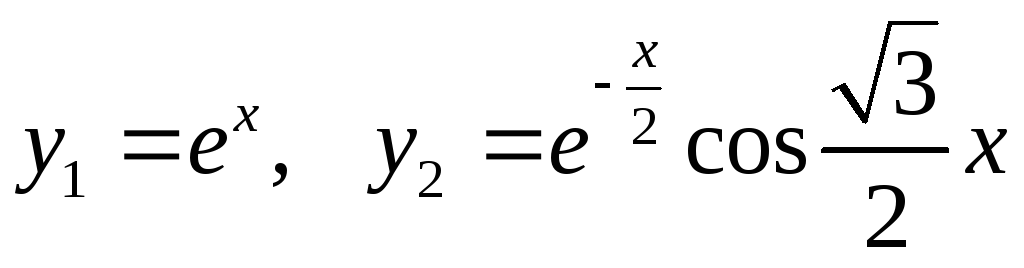 ,
,
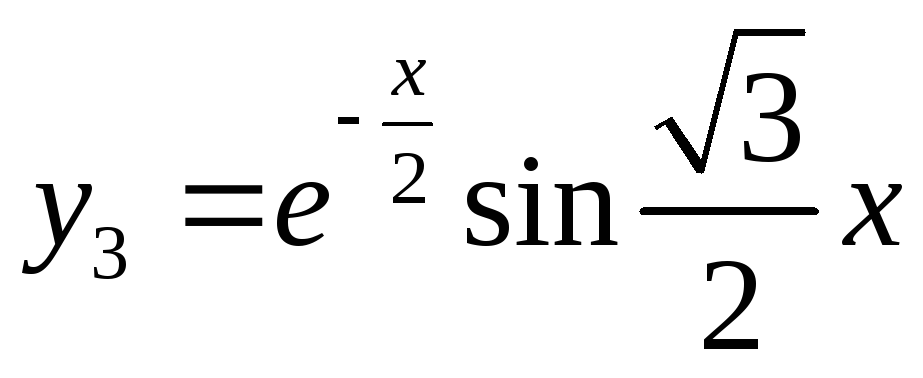 .
.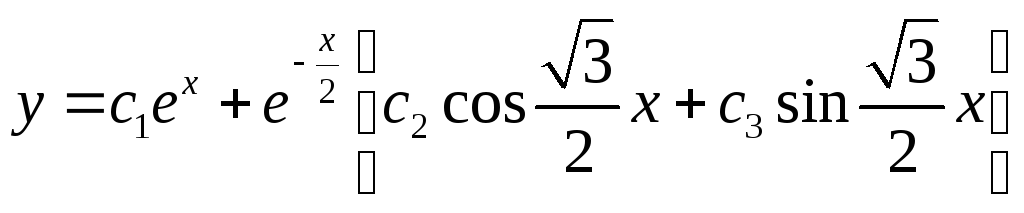 .
.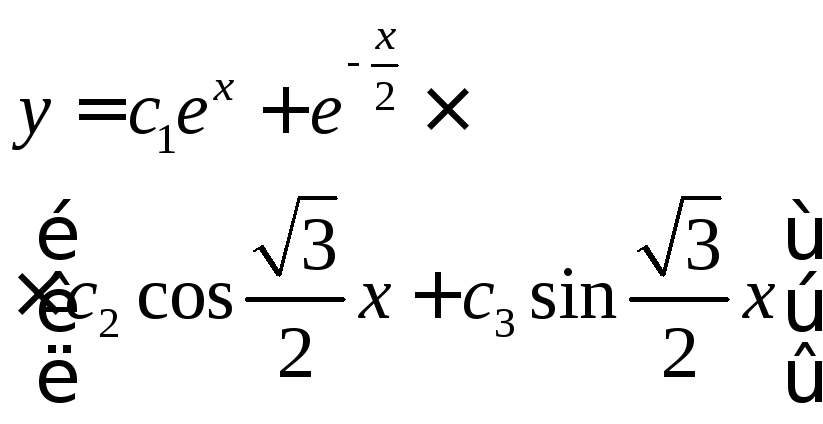
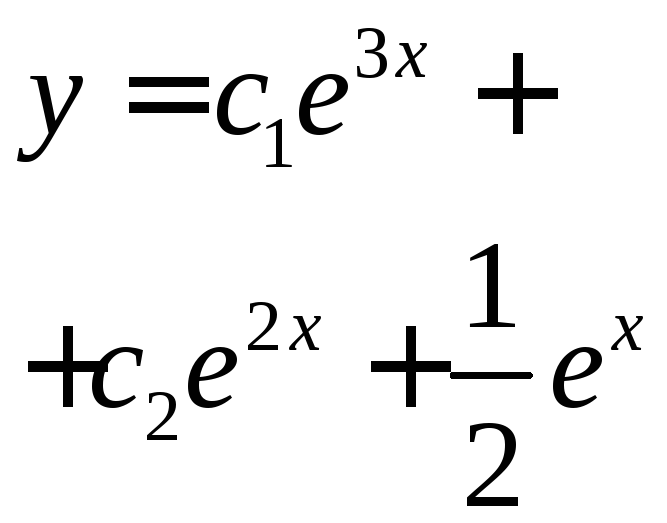
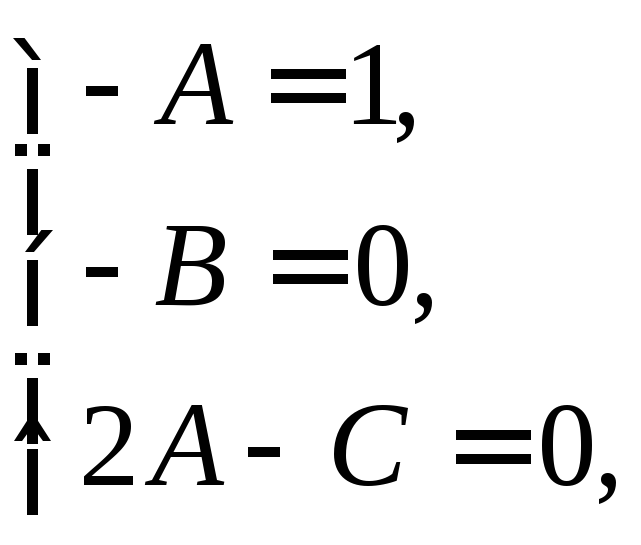 откуда
откуда
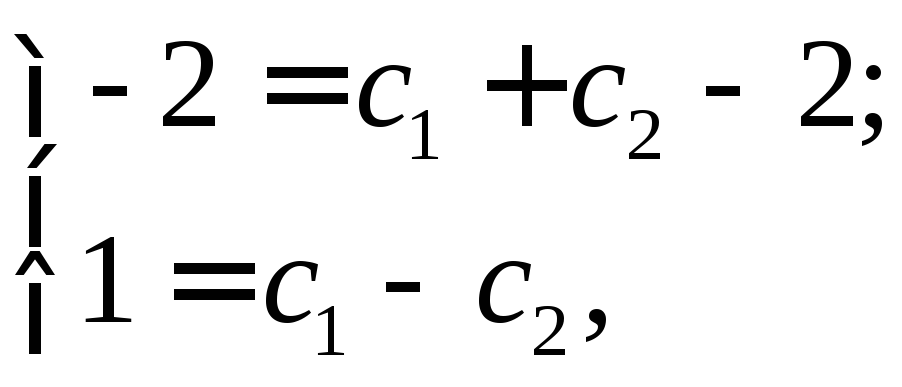
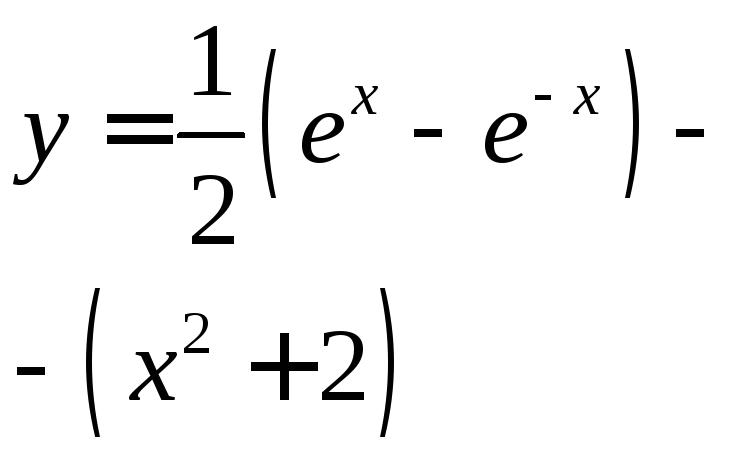
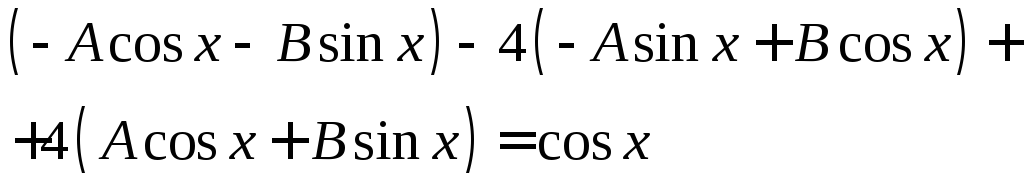 ;
;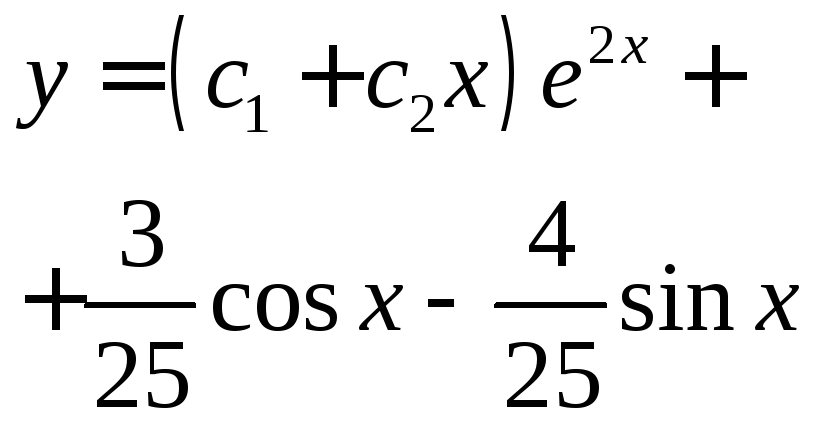
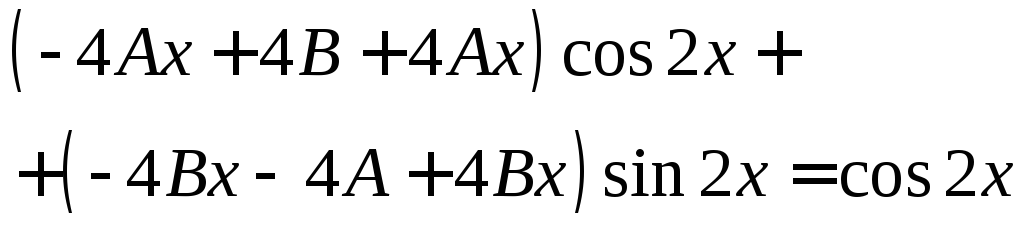 ,
,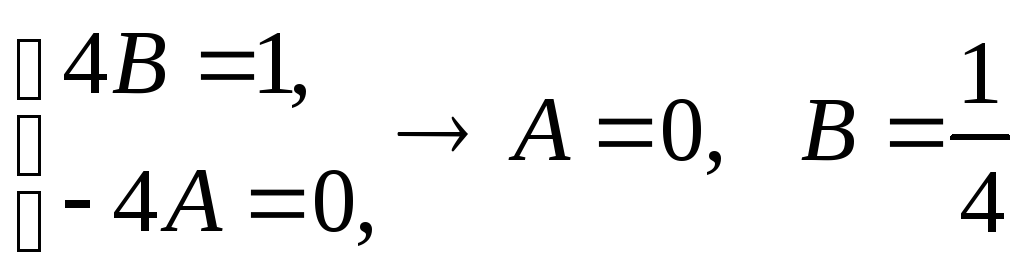 ,
,
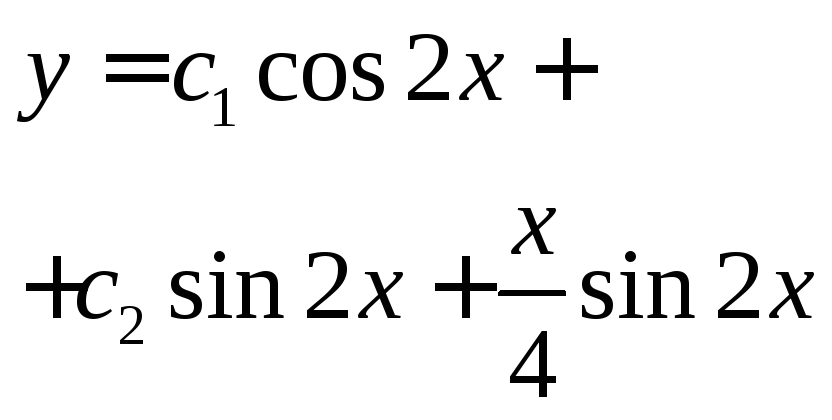
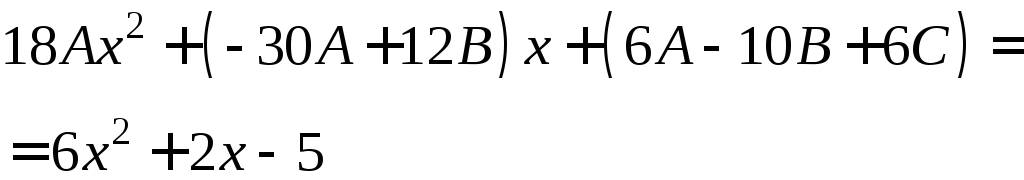 .
.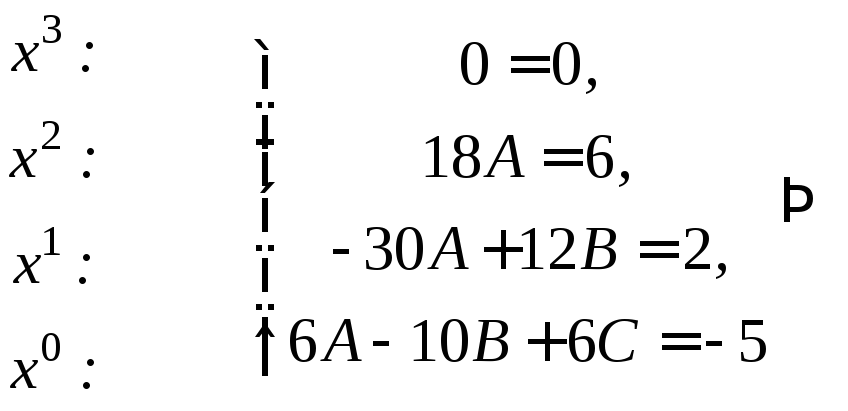
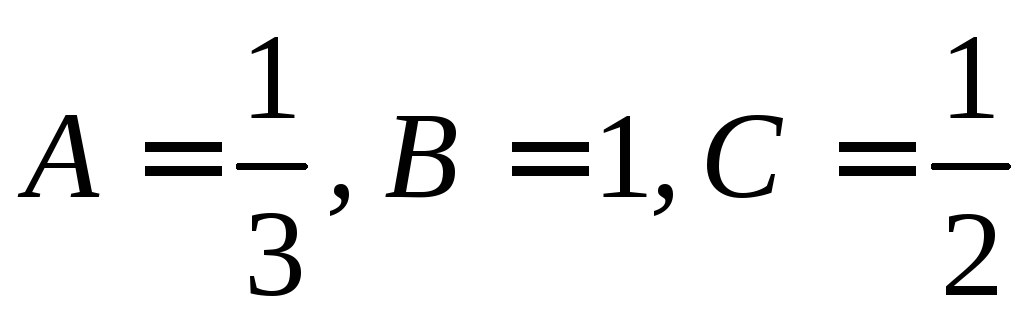 .
.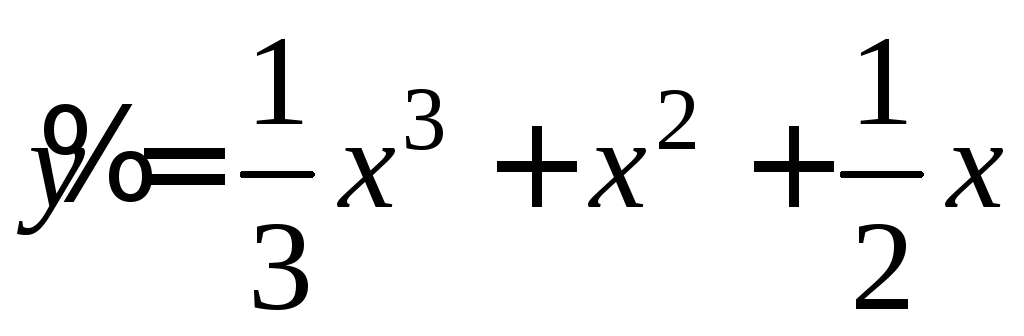 .
.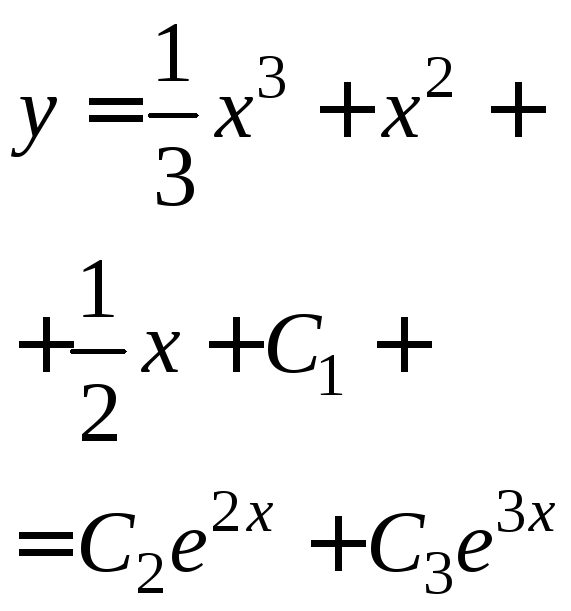

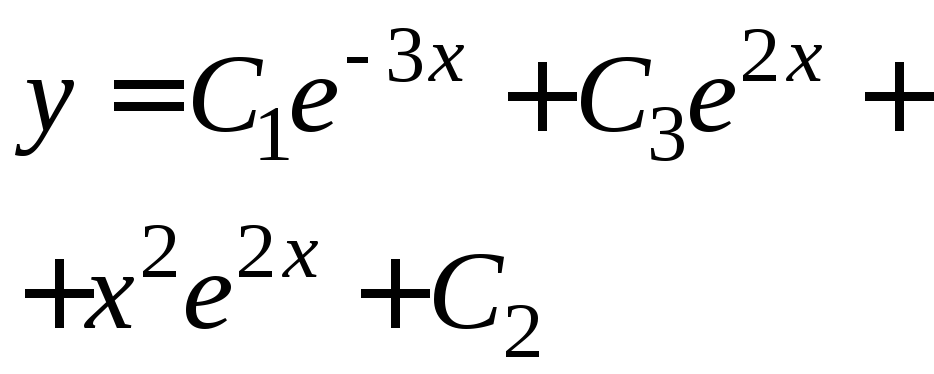
 ,
,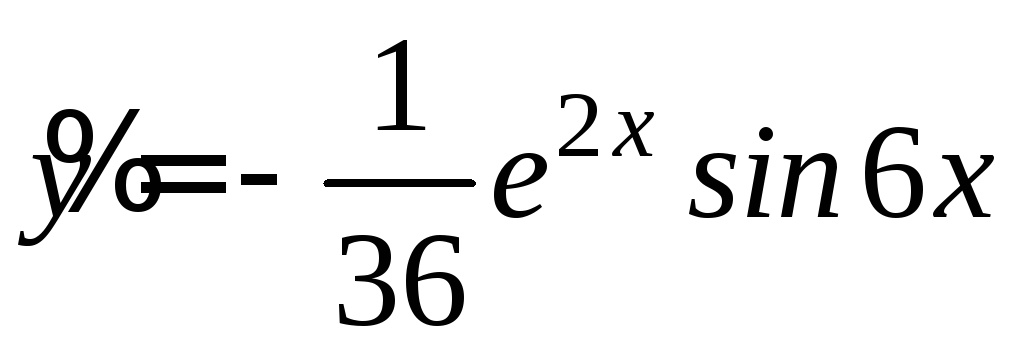 .
.