Тема 1.6. Статика.
Центр тяжести тела
|
Вопросы |
Ответы |
Код |
|
1. Выбрать формулы для расчета координат центра тяжести тела, составленного из объемных частей.
|
|
1 |
|
|
2 | |
|
|
3 | |
|
|
4 | |
|
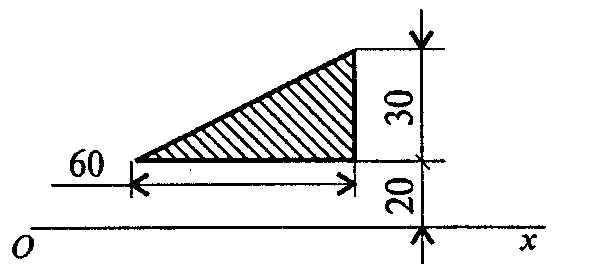
2. Вычислить статический момент данной плоской фигуры относительно оси Ох.
|
9·10³ мм³ |
1 |
|
27·10³ мм³ |
2 | |
|
36·10³ мм³ |
3 | |
|
42·10³ мм³ |
4 | |
|
3. Определить координаты центра тяжести фигуры 2 относительно осей Ох и Оу; а = 80мм;b= 90мм;c= 30мм; d=f=20MM.
|
Xc= 15мм,Yc=30мм |
1 |
|
Xc=- 40 мм, Yc=35 мм |
2 | |
|
Xc=25 мм, Yc=50 мм |
3 | |
|
Xc=- 25 мм, Yc=30 мм |
4 | |
|
4. Определить координатуYcцентра тяжести фигуры 1 (уголок 70×70×5) Относительно оси Ох (фигура 2 - швеллер № 20).
|
64мм |
1 |
|
83 мм |
2 | |
|
95 мм |
3 | |
|
163,5 мм |
4 | |
|
5. Вычислить координатуYcцентра тяжести составного сечения.
|
19 мм |
1 |
|
21 мм |
2 | |
|
17 мм |
3 | |
|
25 мм |
4 |
Темы 1.8, 1.9. Кинематика точки. Простейшие движения твердого тела
Знатьформулы для определения параметров поступательного и вращательного движения и кинематические графики.
Уметь определять кинематические параметры тела при поступательном и вращательном движениях, определять параметры любой точки тела.
Расчетные формулы для определения параметров поступательного движения тела
Все точки тела движутся одинаково.
Закон равномерного движения:
Закон равнопеременного движения:
Здесь S0 - путь, пройденный до начала отсчета, м; υ0 - начальная скорость движения, м/с;
аt - постоянное касательное ускорение, м/с², скорость: υ =S´; υ = υo +at·t.
Ускорение: at = υ'.
Закон неравномерного движения:S= ƒ(t³).
Кинематические графики поступательного движения представлены на рис. П4.1.
Расчетные формулы для определения параметров вращательного движения
Точки тела движутся по окружностям вокруг неподвижной оси (оси вращения).
Закон равномерного вращательного движения: φ= φо + ωt.
Закон равнопеременного вращательного движения:
Зaкoн неравномерного вращательного движения: φ = ƒ(t³). Здесь φ - угол поворота тела за времяt, рад;
ω- угловая скорость, рад/с;
φо - угол поворота, на который развернулось тело до начала отсчета;
ωo- начальная угловая скорость;
ε - угловоеускорение, рад/с²;
Угловая скорость: ω = φ'; ω = ωo+ εt; Угловое ускорение: ε = ω'
Кинематические графики вращательного движения представлен на рис. П4.2.
Число оборотов вращения тела: z = φ/(2π).
Угловая частота вращения: n, об/мин.
Параметры
движения точки вращающегося тела(рис. П4.3):
υ - линейная скорость точки А:
υ= ωr, м/с;
at - касательное ускорение точки А:, at = εr, м/с²;
аn- нормальное ускорение точки А: аn= w²r, м/с².
Рекомендации для решения задач расчетно-графической работы
Задание 5.Частота вращения шкива диаметром d меняется согласно графику. Определить
полное число оборотов шкива за время движения и среднюю угловую скорость за то же время. Построить график угловых перемещений и угловых ускорений шкива. Определить ускорения точек обода колеса в моменты времени tl и t2.
|
|
|
|
|
|
|
|
|
Пара метр |
Варианты | ||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 | |
|
Диа метр шки ва, м. |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,5 |
0,4 |
0,3 |
0,2 |
0,2 |
0,3 |
0,4 |
0,5 |
0,3 |
0,4 |
|
t1, с. |
2 |
1 |
2 |
1 |
3 |
2 |
1 |
2 |
3 |
1 |
2 |
3 |
2 |
1 |
2 |
|
t2, с. |
8 |
9 |
7 |
9 |
8 |
7 |
7 |
8 |
9 |
8 |
9 |
7 |
8 |
7 |
9 |
|
Рис. |
а |
б |
в |
г |
д |
е |
е |
г |
д |
б |
а |
в |
б |
д |
е |
|
Пара метр |
Варианты | ||||||||||||||
|
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 | |
|
Диа метр шки ва, м. |
0,3 |
0,2 |
0,2 |
0,3 |
0,4 |
0,5 |
0,3 |
0,4 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,5 |
0,4 |
|
t1, с. |
2 |
1 |
2 |
1 |
3 |
2 |
1 |
2 |
3 |
1 |
2 |
3 |
2 |
1 |
2 |
|
t2, с. |
8 |
9 |
8 |
9 |
7 |
8 |
7 |
9 |
8 |
9 |
7 |
9 |
8 |
7 |
7 |
|
Рис. |
а |
б |
в |
г |
д |
е |
е |
г |
д |
б |
в |
а |
в |
а |
д |
ТЕСТ ДЛЯ САМОКОНТРОЛЯ.