Лекция 7. Функции непрерывные на отрезке

• Непрерывность функции на множестве

• Первая теорема Вейерштрасса (об ограниченности функции, непрерывной на отрезке)

• Вторая теорема Вейерштрасса (о достижении точных верхней и нижней граней непрерывной на отрезке функции)

• Теоремы о корнях непрерывной функции:

• теорема Больцано - Коши о нуле непрерывной функции

• теорема о прохождении непрерывной на отрезке функции через любое промежуточное значение

• Обратная функция. Теорема о существовании и непрерывности обратной функции

• Непрерывность обратных тригонометрических функций. Непрерывность показательной и логарифмической функции. Графики.

• Определение функции равномерно непрерывной на множестве. Теорема Кантора

7.1 Непрерывность функции на множестве

Определение. Функция называетсянепрерывной на множестве , если она непрерывна в каждой точке этого множества:

.

Пусть ,.

Определение. Точка называетсявнутренней точкой , если.

Определение. Множество называетсяоткрытым, если каждая его точка внутренняя.

Определение. Множество называетсязамкнутым, если – открыто.

 –открыто - замкнутые множества.

Приведем без доказательства теорему.

ТЕОРЕМА. Множество замкнуто(все предельные точки принадлежат).*

* – замкнуто. Пусть– предельная точка. Доказательство проведём от противного. Предположим, что. Тогда,, следовательно, не является предельной точкой множества .

Пусть . Докажем, что– открыто..

–внутренняя точка , следовательно, открыто, поэтому замкнуто.

7.2 Первая теорема Вейерштрасса (об ограниченности функции, непрерывной на отрезке)

Пусть .

Определение. Будем говорить, что непрерывна на (запись: ), еслинепрерывна в любой точке, в точкесправа и вслева.

ТЕОРЕМА 1 (Первая теорема Вейерштрасса)

Функция непрерывная на отрезке, ограничена на нём.

Доказательство. Теорему докажем от противного. Предположим, что не является ограниченной на, то есть

Пусть .

,

,

………………………………

То есть для существует точкадля которой.

Последовательность ограничена, так как все точки. Тогда по теоремеБольцано – Вейерштрасса существует сходящаяся подпоследовательность , причем. По теореме о предельном переходе в неравенствах для последовательностей:, т. е..

Функция непрерывна в точке, поэтому

(1)

(предел по Гейне). Но так как , то

. (2).

Мы пришли к противоречию (сравните (1) и (2)), которое и завершает доказательство теоремы.

Замечание. Для функций, непрерывных на интервале, утверждение предыдущей теоремы, вообще говоря, не верно. В этом легко убедиться, на примере функции . Эта функция непрерывна, но не ограничена на (0,1).

7.3 Вторая теорема Вейерштрасса (о достижении точных верхней и нижней граней непрерывной на отрезке функции)

Пусть , ограничена на множестве и пусть

, .

Тогда для .

Определение. Будем говорить, что функция достигает своей точной верхней грани (нижней грани) на , если.

Пример 1. 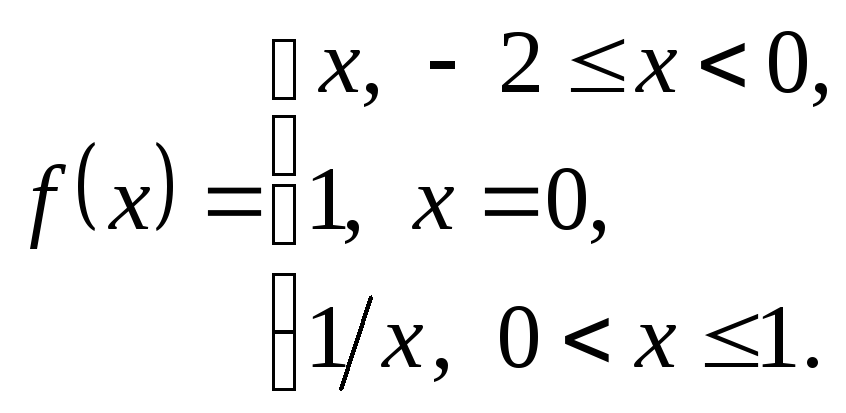Здесь,.

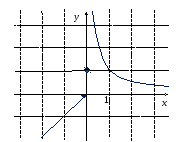
Пример 2. ,

Здесь , но нет числатакого, что.

П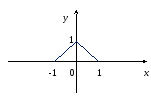ример 3. ,

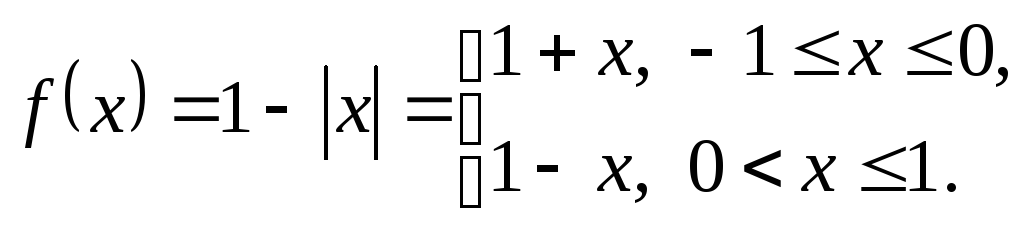
Здесь ,, то естьдостигает точной верхней грани на.

ТЕОРЕМА 2 (Вторая теорема Вейерштрасса)

Если функция непрерывна на отрезке, то она достигает на этом отрезке своей точной верхней и точной нижней граней, то естьтакие, что .

Доказательство. Доказательство проведём от противного. Предположим, что .

Рассмотрим функцию . Так как, то функциянепрерывна на отрезке. Тогда попервой теореме Вейерштрасса , то есть, то естьне является наименьшей верхней границей, то есть супремумом.

Всамом деле, если, то нет, таких, что .

Для точной нижней грани доказательство аналогично.

Таким образом, для непрерывной на отрезке функции можно говорить о максимальном (минимальном) значении:

, .