
- •Лекция 6. Непрерывность функции одной переменной
- •6. 1 Непрерывность функции в точке
- •6.2 Односторонняя непрерывность, связь с непрерывностью в точке
- •6.3 Классификация точек разрыва. Примеры
- •6.4 Свойства непрерывных функций
- •6.5 Арифметические операции над непрерывными функциями
- •6.6 Теорема о непрерывности сложной функции
- •6.7 Непрерывность элементарных функций
- •Лекция 7. Функции непрерывные на отрезке
- •7.1 Непрерывность функции на множестве
- •7.2 Первая теорема Вейерштрасса (об ограниченности функции, непрерывной на отрезке)
- •7.3 Вторая теорема Вейерштрасса (о достижении точных верхней и нижней граней непрерывной на отрезке функции)
- •7.3 Теоремы о корнях непрерывной функции теорема 3 (теорема Больцано-Коши о нуле непрерывной функции)
- •7.4 Обратная функция. Теорема о существовании и непрерывности обратной функции
- •7.5 Определение функции равномерно непрерывной на множестве. Теорема Кантора
- •Глава 3
- •§3.1 Производная функции
- •Бесконечные производные
![]()
![]()
![]()
Лекция 6. Непрерывность функции одной переменной
Непрерывность функции в точке
Односторонняя непрерывность справа и слева, связь с непрерывностью в точке
Классификация точек разрыва. Примеры
Свойства непрерывных функций:
теорема о локальной ограниченности;
теорема об устойчивости знака непрерывной функции в точке
Арифметические операции над непрерывными функциями. Непрерывность многочлена и дробно-рациональной функции
Теорема о непрерывности сложной функции
Непрерывность элементарных функций
6. 1 Непрерывность функции в точке
Определение.
Функция
![]() называется
непрерывной
в точке
называется
непрерывной
в точке
![]() (
(![]() –
предельная точка
–
предельная точка![]() ),
если существует
),
если существует
![]() (1)
(1)
Обратим внимание
на то, что условиями непрерывности
функции в точке
![]() (при записи соотношения (1)) являются:
(при записи соотношения (1)) являются:
1) существование
конечного значения
![]() ;
;
2) существование
конечного
![]() .
.
Так как
![]() ,
то
,
то![]() .
Следовательно, непрерывные в точке
функции (и только они) перестановочны
с операцией предельного перехода (т.
е. можно переходить к пределу под знаком
функции):
.
Следовательно, непрерывные в точке
функции (и только они) перестановочны
с операцией предельного перехода (т.
е. можно переходить к пределу под знаком
функции):
![]() .
.
Определение.
В изолированной
точке
![]() любая функция
любая функция
![]() непрерывна.
непрерывна.
Определение.
Функция
![]() ,
не являющаяся непрерывной в точке
,
не являющаяся непрерывной в точке![]() ,
предельной для
,
предельной для![]() ,
называетсяразрывной
в ней. Точку
,
называетсяразрывной
в ней. Точку
![]() называютточкой
разрыва функции
называютточкой
разрыва функции
![]() ,
причем функция
,
причем функция![]() может быть не определена в этой точке.
может быть не определена в этой точке.
Подставляя сюда определения предела по Коши или по Гейне, получим:
Определение
непрерывности
функции в точке по
Коши:
функция
![]() непрерывна
в точке
непрерывна
в точке
![]() ,
если
,
если![]() .
.
Определение
непрерывности
функции в точке по
Гейне:
функция
![]() непрерывна
в точке
непрерывна
в точке
![]()
![]() .
.
6.2 Односторонняя непрерывность, связь с непрерывностью в точке
Из связи существования предела и односторонних пределов получаем:
Определение.
Функция
![]() называется
непрерывной
слева (справа)
в точке
называется
непрерывной
слева (справа)
в точке
![]() ,
предельной для множества
,
предельной для множества![]() ,
если
,
если
![]() .
.
Критерий непрерывности функции в точке через односторонние пределы.
Функция
![]() непрерывна
в точке
непрерывна
в точке
![]() ,
предельной для множества
,
предельной для множества![]() ,тогда
и только тогда, когда
она непрерывна в этой точке и слева и
справа, то есть
,тогда
и только тогда, когда
она непрерывна в этой точке и слева и
справа, то есть
![]() . (2)
. (2)
Положим
![]() .
.
Величину
![]() называютприращением
аргумента,
а
называютприращением
аргумента,
а
![]() –приращением
функции.
Так как
–приращением
функции.
Так как
![]() ,
то условие непрерывности (1) можно
переписать в виде
,
то условие непрерывности (1) можно
переписать в виде![]() .
Отсюда
.
Отсюда![]() или
или
![]() (3)
(3)
Равенство (3) называется разностным условием непрерывности функции в точке и служит практическим приемом доказательства непрерывности функции в точке.
Пример.
Покажем, что функция
![]() непрерывна в любой точке
непрерывна в любой точке
![]() .
.
Имеем
![]()
![]()
![]() .
.
Значит, функция
![]() непрерывна во всякой
непрерывна во всякой
![]() .
.
6.3 Классификация точек разрыва. Примеры
Пусть функция
![]() ,
,
![]() – предельная точка для множества
– предельная точка для множества![]() .
.
Определение.
Если
![]() (
(![]() может вообще не существовать), то точка
может вообще не существовать), то точка![]() называетсяточкой
устранимого разрыва.
называетсяточкой
устранимого разрыва.
Замечание. В случае устранимого разрыва
![]() . Указанный разрыв
можно устранить, если дополнить разрывную
функцию до непрерывности следующим
образом:
. Указанный разрыв
можно устранить, если дополнить разрывную
функцию до непрерывности следующим
образом:
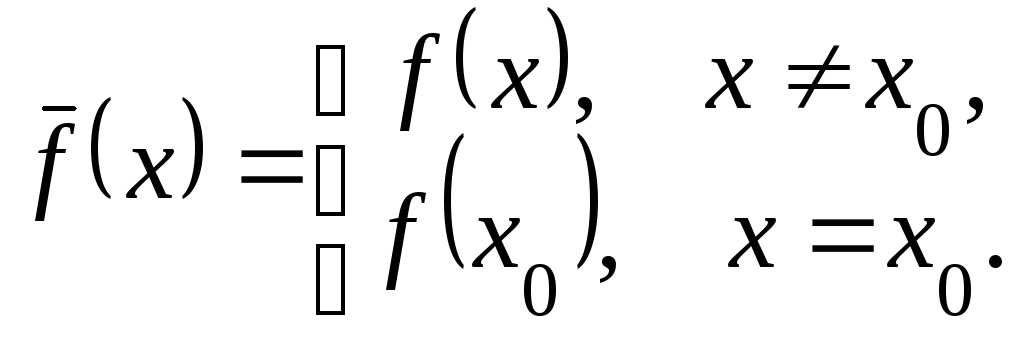
П ример.
Функция
ример.
Функция
![]() имеет в точке
имеет в точке![]() устранимый разрыв, так как
устранимый разрыв, так как
![]() .Здесь
.Здесь
![]() не существует.
не существует.
Если
положить
![]() ,
то получим непрерывную функцию
,
то получим непрерывную функцию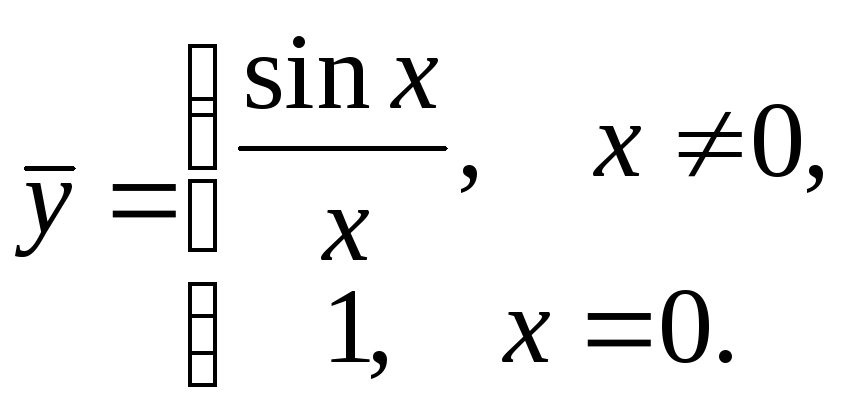
Определение.
Если
существуют конечные односторонние
пределы
![]() ,
не равные между собой
,
не равные между собой![]() (значение
(значение![]() может также не существовать), то точка
может также не существовать), то точка![]() называетсяточкой
разрыва 1 - го рода.
называетсяточкой
разрыва 1 - го рода.
Число
![]() называетсяскачком
функции
называетсяскачком
функции
![]() в точке
в точке
![]() .
.
Во всех остальных
случаях точку разрыва
![]() будем называтьточкой
разрыва 2 - го рода.
будем называтьточкой
разрыва 2 - го рода.
Замечание. В случае разрыва 2 - го рода хотя бы один из односторонних пределов бесконечен или вообще не существует.
Е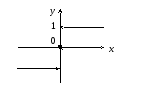 сли
односторонние пределы
сли
односторонние пределы
![]() бесконечны, то точку
бесконечны, то точку![]() иногда называютполюсом.
иногда называютполюсом.
Примеры. 1.
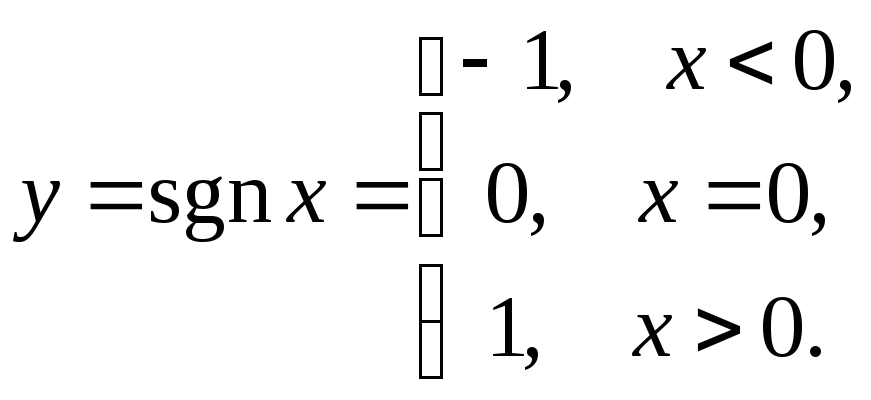
Здесь
точка
![]() - точка разрыва первого рода:
- точка разрыва первого рода:![]() .
Заметим, что скачок функции в этой точке
равен
.
Заметим, что скачок функции в этой точке
равен![]() .
.
2.
Функция
![]() имеет в точке
имеет в точке![]() разрыв второго рода, так как
разрыв второго рода, так как
![]() не существует (см.
пример ).
не существует (см.
пример ).
3.
Исследуем поведение функции![]() .
.
![]() .
.
![]() .
.
Функция
![]() имеет в точке
имеет в точке
![]() разрыв второго рода. Прямая
разрыв второго рода. Прямая![]() является правой вертикальной асимптотой
графика функции(см.).
является правой вертикальной асимптотой
графика функции(см.).
Исследуем поведение функции на бесконечности:
![]() .
Поэтому прямая
.
Поэтому прямая
![]() является горизонтальной асимптотой
графика функции(см.
) Построим
график функции:
является горизонтальной асимптотой
графика функции(см.
) Построим
график функции:
З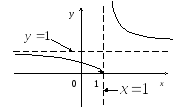 десь
десь
![]() .
.
4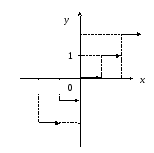 .
Исследуем
поведение функции
.
Исследуем
поведение функции
![]() .
.
Здесь
![]() .
.
Точки
![]() – точки
разрыва первого рода. Функция непрерывна
справа в точках
– точки
разрыва первого рода. Функция непрерывна
справа в точках
![]() .
.
