
Labaratorni_z_fiziki__vidpovidi_na_kontrolni
.pdf
У випадку однорідного тіла правильної форми операцію сумування заміняють на операцію інтегрування. Момент інерції будь-якого тіла можна обчислити через інтеграл:
I = ∫ r 2 dm , |
(1.44) |
( m) |
|
де інтегрування ведеться по всьому об’єму тіла, уявно розбитого на елементарні маси dm , кожна з яких характеризується своїм радіусом r відносно вісі обертання.
Знайдемо моменти інерції деяких тіл.
Момент інерції однорідного стержня відносно осі CC′ ,
що проходить через його центр мас.
|
|
|
|
C |
|
|
|
|
|
|
|
|
x |
dx |
|||
|
|
|
|
|
|
|
|
x |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х1=-l/2 |
|
C′ |
|
|
Х2=l/2 |
||
|
|
|||||||
|
|
|
Рис.1.7 |
|
|
|
|
|
Розглянемо однорідний стержень (рис. 1.7). Нехай його |
||||||||
маса m , довжина l , лінійна густина γ |
(лінійна густина чисельно |
|||||||
дорівнює |
масі, що |
припадає на одиницю довжини стержня |
||||||
γ = m |
). |
Систему |
координат розмістимо таким чином, щоб |
|||||
l |
|
|
|
|
|
|
|
|
через її початок проходила вісь CC′ . Знайдемо момент інерції стержня відносно осі, що проходить через його центр мас. Виділимо на відстані x від осі CC′ , яка проходить через центр мас стержня, елементарну масу dm . Елементарний момент інерції виділеної маси відносно осі CC′ складає: dI C = x 2 dm .
Оскільки dm = γdx ,то dI C = γ x 2 dx , а момент інерції всього стержня
21
|
|
|
X 2 =l / 2 |
|
|
|
|
x3 |
|
l / 2 |
|
|
γ |
|
l 3 |
−l 3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
IC |
= |
∫ |
γ x2 dx = γ |
|
|
|
|
|
|
= |
|
|
|
− |
|
|
= |
|
||||||
|
3 |
|
|
|
|
3 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|||||
|
|
|
X1 =−l / 2 |
|
|
γ l |
3 |
|
|
|
−l / 2 |
|
|
|
|
|
|
|
|
|
|
(1.45) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
= |
= |
ml 2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
12 |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
||||
При |
|
виведенні |
співвідношення |
(1.45) |
враховано, що |
|||||||||||||||||||
γ l = m . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогічно знайдемо момент інерції однорідного стержня |
||||||||||||||||||||||||
відносно |
осі ZZ ′ , |
що |
проходить |
через |
один |
із |
його |
кінців. |
||||||||||||||||
Систему координат розмістимо таким чином, щоб через її початок проходила вісь ZZ ′ .
|
I Z |
X 2 =l |
|
x3 l |
= |
γ l 3 |
= |
ml 2 |
. |
(1.46) |
|
= ∫γ x 2 dx =γ |
3 0 |
3 |
3 |
||||||
|
|
X1 =0 |
|
|
|
|
|
|||
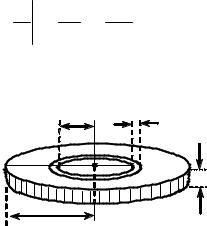
Момент інерції однорідного диска (циліндра) відносно |
||||||||||
вісіCC′ , що проходить перпендикулярно його площині через |
||||||||||
центр C (рис.1.8). Нехай |
|
|
|
х |
|
|
dх |
|
||
маса диска т, радіус диска |
|
|
|
С |
|
|||||
R , густина ρ . Виділимо |
|
|
|
|
|
|
|
|
||
на відстані х |
від центра |
|
|
|
с |
|
|
|
|
|
(точка С) нескінченно |
|
|
|
|
|
|
|
h |
||
тонкий |
обруч |
товщиною |
|
|
|
|
С’ |
|
|
|
dx , елементарний момент |
|
|
R |
|
|
|
||||
|
|
|
|
|
|
|
||||
інерції |
якого |
дорівнює |
Рис. 1.8. Момент інерції диска |
|
||||||
dIC = x 2 dm .
Визначимо елементарну масу dm виділеного елементарного об'єму у вигляді тонкого кільця, беручи до уваги, що густина речовини ρ , а товщина диска h :
|
dm = ρ dV = ρ hdS , |
де |
dS = 2π xdx – площа поверхні виділеного пояска, то |
dIC |
= 2πρhx3 dx . Проінтегруємо останній вираз: |
|
22 |
m |
R |
|
|
|
|
|
|
|
IC = ∫ x2dm = ∫ x2 ρ 2π xdx = |
|
|
|
|||||
0 |
0 |
|
|
|
|
, |
(1.48) |
|
R |
|
|
|
|
|
|||
|
R |
4 |
|
mR |
2 |
|
|
|
= ρ h2π ∫ x3dx = ρh2π |
|
= |
|
|
|
|||
|
|
|
|
|
|
|||
0 |
4 |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
де m = ρπ R 2 – маса диска.
Аналогічно можна знайти момент інерції диска з центральним отвором. Нехай радіус диска R , а радіус отвору r . Для цього рівняння (1.48) необхідно про інтегрувати від r до R
m |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
IC = ∫ x 2 dm = ∫ x 2 ρ 2πrdx = |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
(1.49) |
|||
= ρ h2π ∫ x3 dx = ρh2π R |
4 |
− r |
4 |
= m(R |
2 |
+ r |
2 |
||||||||||||||
) |
|
|
|||||||||||||||||||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
r |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
де m = 2π (R 2 |
− r 2 )hρ – маса диска. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Із (1.49) |
легко знайти |
момент |
інерції |
диска без |
отвору |
||||||||||||||||
( r = 0 ): |
|
|
|
|
+ r 2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
I |
|
= |
m(R 2 |
= |
mR 2 |
|
, |
|
|
|
|
|
|
(1.50) |
||||||
|
C |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
та момент інерції обруча відносно осі, що проходить центр мас
( r ≈ R ) |
|
|
m(R 2 + r 2 ) |
|
|
|
+ R 2 ) |
|
|
|||
I |
|
= |
= |
m(R 2 |
|
= mR 2 . |
(1.51) |
|||||
C |
|
|
|
|
|
|
||||||
|
2 |
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
Момент інерції кулі |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
I |
|
= |
2 |
mR2 . |
(1.52) |
||
|
|
|
|
|
c |
|
||||||
|
|
|
|
|
|
|
5 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
1.2.3.Теорема Штейнера. Ця теорема дозволяє знайти момент інерції тіла відносно довільної осі ZZ ′ , якщо відомий момент інерції даного тіла відносно паралельної осіCC′ , що проходить через центр мас даного тіла (рис. 1.9), а саме:
23
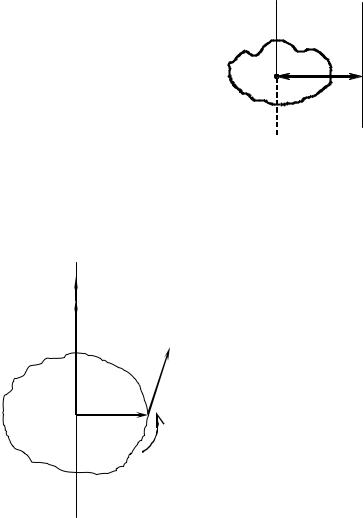
Момент інерції тіла відносно довільної осі ZZ ′ дорівнює сумі моменту інерції
цього |
тіло |
відносно |
|
паралельної |
осіCC′ , |
що |
|
проходить |
через |
центр |
мас |
тіла, і добутку маси тіла на квадрат відстані між цими
осями I z = I c + ma 2 – (1.53),
де m − маса тіла, між осями.
С Z
a
m
C′ Z′
Рис. 1.9. Теорема Штейнера
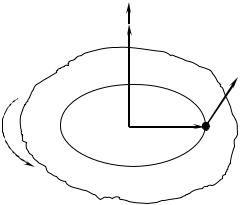
1.2.4. Основне рівняння динаміки обертового руху. Якщо на тіло (рис.1.10), яке може обертатися навколо довільної Z, діє
Z
R = × R
Mz rR F
εR
z
R
F
|
R |
IZ |
r |
|
ω |
Z′
Рис. 1.10
момент сил M Z , а момент інерції цього тіла відносно цієї
ж осі I Z , |
|
то |
тіло |
набуде |
|||
кутового прискорення: |
|
|
|||||
|
|
|
R |
|
|
|
|
R |
= |
M |
z |
|
|
|
|
ε |
|
|
. |
(1.54) |
|||
z |
Iz |
|
|||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Рівняння |
|
(1.54) |
є |
||||
основним рівнянням динаміки обертового руху, в якому відіграє таку ж роль, як і другий закон Ньютона в поступальному русі.
24
1.2.5. Момент імпульсу твердого тіла. Закон збереження моменту імпульсу. Для твердого тіла, яке обертається навколо
осі |
ZZ ′ |
з кутовою швидкістю ω , |
величина моменту імпульсу |
|||||||||
може бути визначена таким чином. |
|
|
|
|
|
|
||||||
|
Уявно |
|
|
Z ′ |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
розіб'ємо |
тіло |
|
|
|
R |
|
|
|
|
|||
|
|
|
|
ω |
|
|
|
|
||||
на |
|
|
|
|
|
|
R |
|
|
|
|
|
нескінченно |
|
|
|
|
Li |
|
|
|
|
|||
|
|
|
|
|
|
R |
= |
R |
||||
малі частинки |
|
|
|
|
|
|
Pi |
miVi |
||||
– |
матеріальні |
|
|
|
|
|
|
|
|
|
||
точки |
(рис. |
|
|
|
|
|
R |
|
|
|
||
1.11). |
|
|
|
|
|
|
ri |
|
|
|
||
|
|
|
|
|
|
|
mi |
|
|
|||
Розглянемо |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
окрему таку i- |
ω |
|
|
|
|
|
|
|
|
|||
точку. Модуль |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
моменту |
|
|
|
Z |
|
|
|
|
|
|
||
імпульсу |
|
|
|
|
|
|
|
|
|
|||
|
Рис. 1.11. Момент імпульсу твердого тіла |
|||||||||||
даної точки з |
||||||||||||
|
|
|
|
|
|
|
|
|
||||
масою Dmi відносно вісі ZZ ′ |
буде |
|
|
|
|
|
|
|||||
|
|
|
DL = Dm r V sinα = Dm |
ω r 2 |
, |
|
(1.55) |
|||||
|
|
|
i |
i i |
i |
|
i |
i |
|
|
|
|
де α = 90O , ω = V 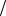 r .
r .
Для всього тіла матимемо (індекс z біля L означає, що
момент імпульсу обчислено відносно осі ZZ ′ ): |
|
||
Lz = ∑Dmi ri |
2ω . |
(1.56) |
|
|
|
z |
|
де ωz – кутова швидкість обертання тіла відносно вісі ZZ ′ . |
|
||
n |
2 = Iz , тому: |
|
|
Згідно з (1.42) ∑ mi ri |
|
||
i =1 |
|
|
|
R |
|
|
|
|
R |
|
|
Lz = Iz ×ωz |
|
(1.57) |
|
|
25 |
|
|
Закон збереження моменту імпульсу: момент імпульсу замкнутої системи тіл залишається сталим незалежно від взаємодії її складових
n |
n |
R |
R |
L = ∑Li |
R |
= const , |
|
= ∑Iiωi |
(1.58) |
||
i=1 |
i =1 |
|
|
де ωi – кутова швидкість i-го тіла, Ii – його момент інерції.
Закон збереження моменту імпульсу посідає важливе значення в механіці. У рівнянні (1.58) постійним залишається, як модуль моменту імпульсу так і його напрямок. На останній властивості ґрунтується робота гіроскопа. Гіроскоп це масивне тіло, яке може вільно обертатися з великою кутовою швидкістю навколо трьох осей. Основна його властивість: вісь гіроскопа зберігає свою орієнтацію в просторі незалежно від орієнтації основи гіроскопа. Гіроскопи широко застосовуються у навігації .
На основі закону збереження моменту імпульсу також пояснюється рух велосипедиста (мотоцикліста ). При русі велосипедиста (мотоцикліста ) вектор моменту імпульсу зберігає свою орієнтацію в просторі і велосипедист не падає.
26
2. ЛАБОРАТОРНІ РОБОТИ З РОЗДІЛУ “ МЕХАНІКА”
Лабораторна робота 1.1 Абсолютно пружний центральний удар куль
Мета роботи. Вивчення законів збереження при абсолютно пружному ударі куль.
Прилади і матеріали. 1. Установка для визначення часу пружного удару куль. 2. Штангенциркуль. 3. Лінійка. 4. Транспортир.
Теоретичні відомості
Установка для визначення часу пружного удару куль
(рис.2.1.1) складається з двох |
однакових абсолютно пружних |
||||||||||||
|
|
|
|
|
|
|
|
стальних куль, підвішених на |
|||||
|
|
|
|
|
|
|
|
провідниках |
|
|
|
однакової |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
довжини. |
|
|
Провідники |
||
|
|
|
|
|
|
|
|
підключені |
до |
конденсатора |
|||
|
|
|
|
α |
|
|
|
через електричний |
опір |
R . |
|||
|
|
l |
|
|
|
|
|||||||
|
|
|
|
|
|
|
Конденсатор |
|
|
можна |
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
підключати |
до |
джерела |
для |
||
|
|
|
|
|
|
|
|
зарядки, або розряджати на |
|||||
m1 |
|
|
|
|
гальванометр |
за допомогою |
|||||||
|
|
|
|
перемикача |
Ï |
|
(рис. 2.1.2). |
||||||
|
|
|
|
|
|
|
|
|
|||||
h |
m1 |
m2 |
|
Відведемо |
|
ліву |
кульку |
||||||
|
|
|
|
установки m1 |
від положення |
||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
рівноваги |
на |
|
кут |
α , |
|
|
|
Рис. 2.1.1 |
|
|
зарядимо конденсатор |
та |
|||||||
|
|
|
|
|
|
|
|
відпустимо |
її. |
|
Рухаючись із |
||
швидкістю V1 , вона зазнає абсолютно пружного центрального удару з нерухомою правою кулькою V2 = 0 . Під час удару куль конденсатор частково розрядиться.
27
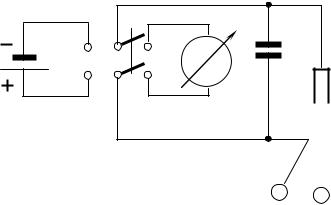
П
G
E |
С |
R
m1 |
|
|
|
m2 |
|
||||
Рис.1.1.2 |
|
|
|
|
При абсолютно пружному центральному ударі куль |
||||
однакової маси (m1 = m2 = m) із рівнянь (1.26) і (1.27), маємо: |
||||
U1 = V2 ; U 2 = V1 , |
(2.1.1) |
|||
де U1 , U2 - відповідно швидкість першої та другої кульки після
удару.
Отже, при зіткненні двох однакових абсолютно пружних куль відбувається обмін швидкостями.
Скористаємося цією обставиною для визначення середньої сили зіткнення куль. Із другого закону Ньютона (1.5а) маємо:
FCτ = DP,
звідки |
|
|
|
D(mV ) |
|
|
|
|||
|
F = |
DP = |
= |
m × DV |
, |
|||||
|
|
|
|
|
||||||
|
C |
τ |
|
|
τ |
|
τ |
|||
|
|
|
|
|
|
|
|
|
|
|
де τ – |
час зіткнення куль; |
V – зміна швидкості першої кулі при |
||||||||
ударі, |
але DV = V1 -U1 = V1 -V2 = V1 , |
тому що U1 = V2 ,a V2=0. |
||||||||
Остаточно одержуємо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
F = |
mV1 |
|
, |
(2.1.2) |
|||
|
|
|
τ |
|||||||
|
|
|
C |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
28
Масу кулі можна визначити за її густиною та об'ємом:
m = ρV = 4 πR3 ρ . 3
Знайдемо швидкість V1 кулі в момент удару (рис.2.1.1). Куля, відведена від положення рівноваги на кут α , має запас
потенціальної |
енергії |
Wn |
= mgh Ця енергія |
при |
ударі |
цілком |
|||||||||||
|
|
|
|
|
= W |
|
= |
|
mV 2 |
|
mgh = |
|
mV 2 |
||||
переходить у |
кінетичну: |
W |
|
|
|
|
1 |
|
або |
|
1 |
|
, |
||||
n |
K |
|
|
2 |
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
звідки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V1 = |
|
|
|
|
|
|
|
|||||||
|
|
|
2gh |
|
|
|
|
|
(2.1.3) |
||||||||
Висоту |
h, з |
якої |
падає |
куля, |
можна |
визначити |
за |
||||||||||
відстаннюl (довжиною маятника) від точки підвісу до центра
маятника та |
кутом відхилення α |
маятника від |
положення |
|||
рівноваги |
h = l(1− cosα ) . |
|
||||
|
(2.1.4) |
|||||
Отже |
|
|
|
|
|
|
|
V1 = |
|
. |
|
||
|
2gl(1− cosα ) |
(2.1.5) |
||||
Час зіткнення τ настільки малий, що його неможливо |
||||||
виміряти |
секундоміром. |
Його |
|
визначають |
методом |
|
конденсаторного хронометра, суть якого полягає в наступному. Кулі при ударі замикають електричне коло, що складається з зарядженого конденсатора та опору R , послідовно з'єднаних між собою. Нехай у початковий момент часу t конденсатор мав заряд
q. За час |
dt при ударі заряд конденсатора зменшиться на dq. |
||
Миттєве |
значення струму при ударі I = − |
dq |
, а відповідно |
|
|||
|
|
dt |
|
зменшення заряду конденсатора dq=-Idt. Миттєве значення
струму може бути визначене з закону Ома I = U , але U = q , де
R C
29
С – ємність конденсатора, R – електричний опір кола. Тоді
− dq = |
q |
|
dt . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
RC |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розділимо змінні і проінтегруємо: |
|
|
|
|
|
|
||||||||||
|
q |
dq |
τ |
|
dt |
|
q |
|
τ |
|
|
|
|
q |
|
|
||
−∫ |
|
|
= ∫ |
|
|
|
ln |
0 |
= |
|
, |
звідки τ |
= CR ln |
|
0 |
, |
||
|
q |
|
|
q |
|
|
|
|||||||||||
q0 |
0 |
|
RC |
|
|
CR |
|
|
|
|
q |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де q0 – |
початковий заряд конденсатора, |
q – |
величина заряду, що |
|||||||||||||||
залишилася на конденсаторі після удару куль. |
|
|
|
|
||||||||||||||
|
|
Для |
|
визначення |
|
величини |
заряду |
конденсатора |
||||||||||
користуються балістичним гальванометром, покази якого n
пропорційні величині заряду |
q0 |
= |
n0 |
, отже: |
|
||
|
|
|
|
||||
|
q |
n |
|
||||
τ = CR ln |
n0 |
, |
(2.1.6) |
||||
|
|||||||
де n0 − покази гальванометра |
|
|
n |
|
|||
|
при розряді |
зарядженого |
|||||
конденсатора через гальванометр до удару куль, n − покази гальванометра при розряді конденсатора із залишковим зарядом через гальванометр після удару куль (конденсатор в обох випадках заряджається від джерела з однаковою ЕРС).
Порядок виконання роботи
Для визначення часу, середньої сили і швидкості співударяння куль необхідно:
1.Відвести одну з куль і закріпити її засувкою. Зарядити конденсатор від джерела і розрядити його через гальванометр. Записати покази гальванометра n0..
2.Не змінюючи напругу зарядити конденсатор. Провести удар куль. Заряд конденсатора, що залишився,
розрядити через гальванометр і записати покази n. Дослід повторити 7-9 разів. Результати внести в таблицю 2.1.1.
30
