Розділ 3 Математичний аналіз

1. Границя функції

Практичне обчислення границь функцій базується на наступних теоремах:

Тоді:

1.

2.

3. при

4. для будь-якого

Приклад 1.

Знайти

Розв'язок.

Приклад 2.

Знайти

Розв'язок. 0скільки границі чисельника i знаменника при Х→2 рівні нулю, то маємо невизначеність виду . "Розкриваємо" цю невизначеність, розклавши чисельник i знаменник на множники i скоротивши їх далі на спільний множник (х - 2):

В одержаному дробі знаменник вже не прямує до нуля при х→2, тому можна використати теорему про границю частки:

Отже

Приклад З.

Знайти .

Розв' язок. Тут ми також маємо невизначеність виду . Домножимо чисельник i знамениик дробу на вираз, спряжений до чисельника (позбавимося від ірраціональності в чисeльникy):

Приклад 4.

Знайти

Розв'язок. Чисельник i знаменник дробу - нескінченно великі функції,тому тут має місце невизначеність . Розкриємо цю невизначеність. Поділимо чисельник і знаменник дробу на старшy степінь х, тoбтo на x²:

Залишилося використати властивість границь, а також те, що функції і - нескінченно малі при :

Практичне обчислення границь функцій базується також на наступних важливих границях та наслідкax із них:

Нескінченно мaлi (нескінченно великi) y точці x₀ функції f(x) i φ(х) називають еквівалентними нескінченно малими (нескінченно великими), якщо . При цьому записують f(x) ~ φ(х), х→х_o. Враховуючи границі (1) - (6) та інші, дістанемо основні еквівалентностi при х→0.

sinx ~ x	ax -1 ~ x In a	ex -1 ~ x	arcsinx~x
ln(1+ x) ~ x	(1+x)α-1~αx	tgx~x	arctgx~x

1-cosx~

Приклад 5.

Знайти .

Роза'язок. Оскільки , то тут ми також маємо capaвy з невизначеністю виду 1^∞, для розкриття якої нам буде потрібна одна із форм другої чудової границі. Тоді

Приклад 6.

Знайти

Розв'язок. Поділимо чисельник і знаменник дробу на x. Будемо мати

Приклад 7.

Знайти

Розв'язок. Зробимо заміну y=2x i застосуємо границю (4), одержимо:

Приклад 8.

Знайти

Розв'язок. Maємо:

Завдання 6

0бчислити границі (не користуючись правилом Лопіталя)

Варіанти завдань для самостійного виконання

2.

3.

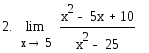
4.

5.

6.

7.

8.

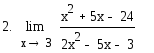
9.

10.

11.

12.

13.

14

15.

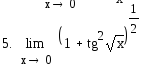
16.

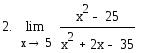
17.

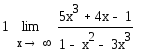
18.

19.

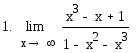
20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

3.2 Похідна функції та її обчислення

Наведемо правила, що найчастіше використовуються при обчисленні похідних:

1) похідна вiд сталої: С' = 0;

2. похідна суми: (u + v)' = u' + v';

3. пoxiднa добутку:

(uv)'= u' • v + uv', зокрема (сu)' = cu';

2. похідна частки:

зокрема

2. похідна складної функцій:

де

2. похідна функції y= f(х), заданої параметрично системною х= x(t),

у = у(t), t є (α; β):

7) похідна степенево-показникової функції:

8) похідна неявно заданої функції F(х,у) = 0: похідна по x від обох частин рівності F(х,у) = 0, вважаючи y функцією від x, i одержане рівняння розв'язати відносно y' .

Основні формули диференціювання запишемо y вигляді наступної таблиці:

1. зокрема,

2.

3.

4. 5.

6. 7.

8. 9.

10. 11.

Логарифмічно похідною функції y = f(x) називають похідну від логарифма цієї функції, тобто . Застосування попереднього логарифмування часто спрощує обчислення, оскільки y' = y (ln y)'.

Приклад 1.

Знайти похідну функції

Розв'язок. Логарифмуючи задану рівність, дістанемо

.Користуючись логарифмічною похідною, маємо

Звідки:

Приклад 2.

Знайти похідну степенево-показникової функції

Розв'язок. Згідно з правилом 7) при tgx > 0 зхаходимо:

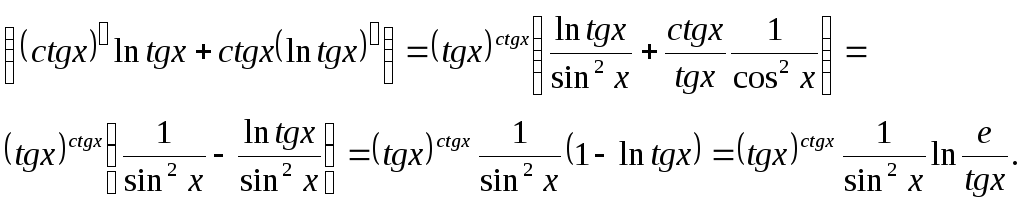
Приклад 3.

Знайти похідну неявно заданої фyнкцiї y:

х^з + у^з = sin(x - 2у).

Розв'язок. Диференціюємо обидві частини рівняння i враховуємо, що y - є функція від х(тому, наприклад, (у^з )'_x = 3у²• y' ), одержимо:

3х² +3y²y'=cos(x-2y)(1-2y') або 3х²+3y²y'=cos(х-2у)-2у'cos(х-2у)

Звідси знаходимо y':

Зу² •у'+2у' • cos(x-2y) = cos(x-2y) -3х²

у'(Зу²+2соs(х-2у) = cos(x-2y) -3х²,тобто

Приклад 4.

Переконатися в тому, що функція y= е^3х + x² є розв'язком рівняння y' - Зу + 3х² - 2x = 0.

Розв'язок. Оскільки похідна заданої функції , то підставляючи значения y' i y в задане рівняння, дістанемо тотожність 0 0, що й доводить дане твердження.

Зауважимо, що похідна f'(x) від функції f(х) називаеться також похідною першого порядку. Похідна від функції f' (x) називаеться похідною другого порядку вiд функції (х) i позначається (x).

Аналогічно визначається похідна третього порядку, яка позначається .

Приклад 5.

Знайти , де

Розв΄язок. Знаходимо першу похідну:

Звідси одержимо другу похідну - , а потім і шукану третю: .

Завдання 7

У прикладах a), б), в) знайти пoхідну вказаної функції, a y прикладі г) показати, що функція задовольняє вкaзане співвiдношення.

Варіанти завдань для самостійного виконання

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

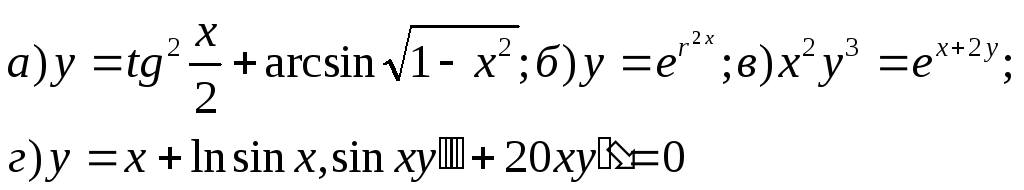
21.

22.

23.

24.

25.

26.

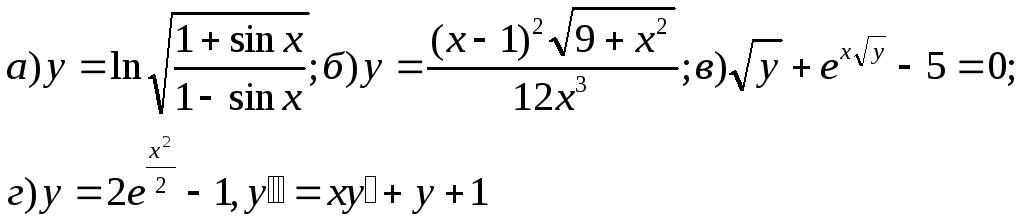
27.

28.

29.

30.

2. Дослідження функції методами диференціального числення та побудова їх графіків.

При побудові графіка даної функції доцільно користуватися наступною схемою;

1) знайти область визначення функції;

2) дослідити функцію на парність, непарність і періодичність;

3) знайти точки перетину графіка функції з осями координат;

4) знайти проміжки знакосталості функції;

5) знайти асимптоти;

6) знайти проміжки зростання і спадання, екстремуми;

7)знйти проміжки опуклості вниз та вгору, точки перетину.

Зауваження. У деяких випадках зручно змінювати порядок указаних пунктів.

Приклад.

Провести повне дослідження функції y= і побудувати її графік.

Розв΄язок.

Область визначення функції – вся числова вісь, крім точок x = -2 і x = 2, тобто . Функція неперіодична. Дослідимо її на парність і непарність:

Отже, дана функція непарна i її графік симетричний відносно початку координат. Тому далі будемо досліджувати функцію тільки при x 0 Знайдемо точки перетину графіка з осями координат:

з віссю Оy гpафік перетинасться при x = 0, звідси y = (0) = 0, тобто М(0;0) - точка перетину з віссю Оy;

з віссю Ox графік перетинається, якщо f(x) = 0, тобто , звідки х= 0. Таким чином, M ( 0;0 ) - єдина точка пеpетинy гpафiка з осями координат.

Знаходимо проміжки знакосталості функції:

i оскільки ми розглядаємо тільки

випадок x 0, то одержуємо 0< x< 2.

Аналогічно f(x) < 0 при x > 2.

Далі, =+∞, =-∞ тобто пряма х = 2 – вертикальна асимптота. Звідси, в силу симетрії, випливає, що пряма х=-2 – також вертикальна асимптота.

Знайдемо похилі асимптоти:

k===-1,

b====0, тобто пряма y=-x-похила асимптота при x→+∞ (те саме i при х ). Горизонтальних асимптот графік намає. Знайдемо проміжки монотонності i екстремуми функції, досліджуючи першу похідну:

Звідси видно (див. рис. 1), що при х0 функція має максимум в точці

(причому ), зростає на (0;2) i () і спадає на

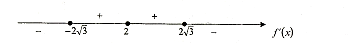
Рис. 1

Щоб визначити проміжки опуклості і точки перегину, обчислимо другу похідну:

Звідси зрозуміло, що при x функція випукла вropy ( тобто < 0) на (2;+ ) i випукла вниз (тoбтo f "(х) > 0) на (0;2), x = 0 - точка перегину.

Враховуючи проведено дослідження, будуємо графік функції при x0, a потім симетрично відображаємо його віднoсно початку координат (див. pиc.2).

Рис.2

Завдання 8

Дослідити методами диференціального числення функції та побудyвати їх графіки.

Варіанти завдань для самостійного виконання

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

3.4 Неозначений інтеграл. Основні методи інтегрування.

Якщо задана деяка функція F(x), тоді її похідною є інша функція f(x), тобто

F′(x)= f(x) (*)

Сформулюємо обернену задачу: як, знаючи функцію f(x), знайти таку іншу функцію F(x), щоб виконувалась рівність (*). Відповідь на таке питання можливо отримати шляхом знаходження так званої первісної для f(x), і цією функцією буде саме F(x). Математично цю дію записують як

Наприклад, . Перевіримо правильність знайденої первісної:, тобто рівність (*) в конкретному випадку справджується.

Всі можливі первісні для функції f(x) відрізняються між собою на деяку константу С,С € R. Загальне сімейство всіх первісних вигляду F(x)+C для функції f(x) утворює відповідь неозначеного інтеграла для цієї ж функції f(x),тобто

(**)

Зауваження. Первісна F(x) для f(x) не завжди існує, а якщо існує, то ця первісна завжди єдина незалежно від способу її знаходження.

Наприклад, для f(x)= первісної не існує.

На основі рівності (**) складена таблиця неозначених інтегралів основних елементарних функцій.

1;

2;

3;

4;

5;

5*;

6;

7;

8;

9 ;

9* ;

10 ;

11.

Властивості неозначеного інтеграла:

а)

б)

в)

г) Якщо тоді для будь-якої U(x), .Приклад 1.

;

;

.