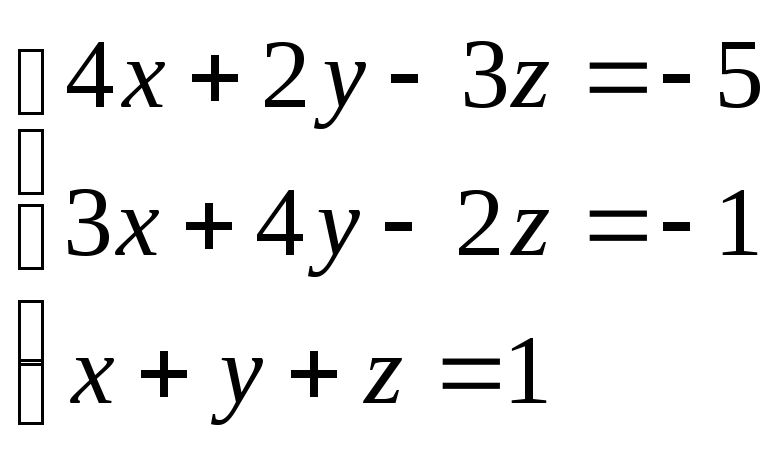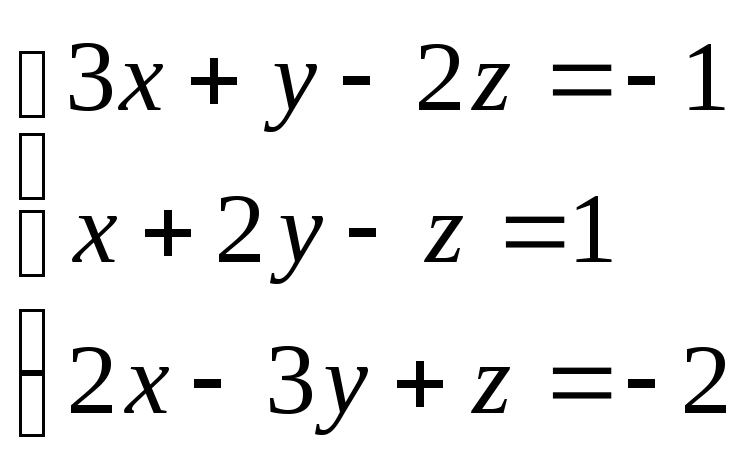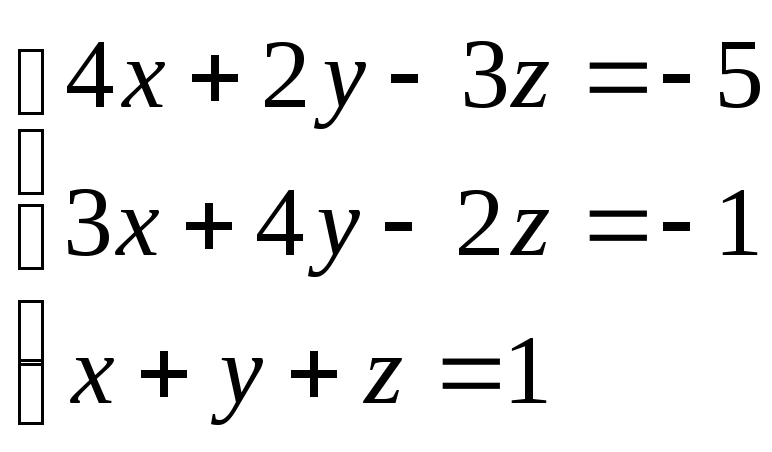1.2 Системи лінійних рівнянь та методи їх розв’язків.

Система лінійних рівнянь - сукупність скiнченної кількості лінійних рівнянь, розв'язком яких вважають точку, що є розв'язкoм кожного її рівняння. Зокрема, систему тpьох лінійних рiвнянь з тpьома змінними (невiдoмими) зaписyють y вигляді:

(1)

де і- задані коефіцієнти системи.Числа називають також вiльними членами системи.

1. Метод Крамера.

Формули Крaмеpа для системи (1) мають вигляд:

, де

-визначник системи (1), а

, ,- визначники, які дістають з визначникаΔ заміною першого, другого і третього стовпців відповідно стовпцем вільних членів.

Приклад 1.

Користуючись формулами Крамера, pозв'язaти систему pівнянь:

Розв'язок. 0бчислимо визначники системи:

, ,

,

Тоді за формулами Крамера

Таким чином, x = -1, y = 0 , z = 2 - розв'язок системи.

2. Матричний метод

Система лінійних рівнянь можна записати у вигляді матричної рівності

де - квадратна матриця порядку, складена з коефіцієнтів при невідомих, матриця розмінності , складена з невідомих; матриця розмірності , складена з вільних членів.

Розвязком не виродженої системи лінійних рівнянь записаної у вигляді матричної рівності знаходять за формулою:

Приклад 2

Розв’язати систему рівнянь

методом оберненої матриці.

Розвязок

Запишемо систему в матричному вигляді де

, ,.

Для матриці А обернену ми побудували в попередньому прикладі, тому маємо:

.

Отже, x₁ = 1, x₂ = 2, x₃ = –1 — розв’язок системи.

Завдання 2

1. Рoзв'язати системи лінійних рівнянь методом Крамера.

2. Рoзв'язати системи лінійних рівнянь матричним методом.

3. Рoзв'язати системи лінійних рівнянь методом Гаусса.

Варіанти завдань для самостійного виконання.

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.

Розділ 2 Аналітична геометрія

2.1. Вектори, типи добутків векторів та методи їх розв’язування.

До лінійних належать такі операції над векторами:

• множення вектора на скаляр . При цьому одержаний век­торгеометрично, залежно від величини і знака, розтягується, стискається, змінює напрям ;

• додавання векторів. Дія виконується за правилом паралело- грама або трикутника.

Якщо вектор задано в координатній формі, то у разі множення його на скаляр всі координати треба помножити на цей скаляр, а в разі додавання — додати відповідні його координати.

Cкалярного добутку векторів: ;

,

Кут  між векторами: ,

умови паралельності та перпендикулярностідвох векторів.

За використання векторного добутку слід пам’ятати, що він некомутативний, а його модуль дорівнює площі паралелограма, побудованого на векторах-множниках. Знаходять векторний добуток за формулою:

.

Геометричний зміст мішаного добутку полягає в тому, що його модуль дорівнює об’єму паралелепіпеда, побудованого на векторах добутку.

.

У зв’язку з цим його часто використовують для знаходження об’єму і перевірки компланарності трьох векторів

Приклад 1.

Обчислити довжини діагоналей паралелограма, побудованого на векторах і, якщо відомо, що.

Розвязок.

З визначення операції додавання векторів відомо, що одна діагональ паралелограма ,а друга .Довжина довільного вектора визначається за формулою: . Тоді:

Приклад 2.

 Дано три послідовні вершини паралелограма: . Знайти його четверту вершинуі кут між діагоналями.

Розвязок.

Нехай шукана вершина має координати . З умови колінеарності векторіві маємо: , або. Згідно з властивостями паралелограмаабо. Діагоналі паралелограма дорівнюють відповідно сумі і різниці векторів-сторін;. Кут між діагоналями знайдемо за формулою:

соs  отже,.

Приклад 3.

Знайти площу паралелограма, діагоналями якого є вектори і, деі— одиничні вектори, а кут між ними дорівнює 45.

Розвязок.

Позначимо через сторони паралелограма, тоді, звідки. Площу паралелограма знайдемо як модуль векторного добутку. Отже,.

Приклад 4.

Знайти площу і висоту трикутника, вершинами якого є:_{Розвязок}

Знайдемо вектори і. Модуль їх векторного добутку буде дорівнювати подвоєній площі трикутника:звідки.

Знайдемо висоту трикутника: .

Приклад 5.

Для піраміди з вершинами ,обчислити об’єм, площу граніАВС і висоту, опущену на цю грань.

Розвязок.

Знайдемо вектори .Модуль мішаного добутку у шість разів більший за об’єм піраміди, побудованої на векторах, тобтоДля обчислення площі гра- ніАВС знайдемо . Тоді, а висота піраміди .

Варіанти завдань для самостійного виконання.

1. Знайти кут між векторами .

2. При якому значенні  вектори ібудуть перпендикулярними, якщо

3. Визначити кути трикутника з вершинами ,і.

4. У трикутнику з вершинами знайти кут, утворений стороноюОВ і медіаною ОМ.

5. Який кут утворюють одиничні вектори і, якщо векториівзаємно перпендикулярні?

6. Знайти проекцію вектора на вісь, що має напрям вектора, деівзаємно перпендикулярні орти. Обчислити кути між віссю проекції і ортамита.

7. Знайти кут між діагоналями паралелограма, побудованого на векторах .

8. Обчислити , якщо.

9. Дано компланарні вектори , причому і.

Обчислити модуль вектора .

10. Задано вектори і. Знайтиі.

11. Обчислити довжини діагоналей паралелограма, побудованого на векторах , де.

12. Дано вектор , де. Знайтиі.

13. Дано точки . Побудувати векториіта знайти.

14. Визначити кут між бісектрисами двох плоских кутів правильного тетраедра, які проведені з однієї вершини.

15. З вершини прямокутника зі сторонами 6 і 4 проведено прямі, що ділять протилежні сторони навпіл. Знайти кут між ними.

16. Обчислити площу і висоту паралелограма, побудованого на векторах .

17. Вектори іутворюють кут, що дорівнює 45. Знайти площу і одну з висот трикутника, побудованого на векторах і, якщо.

18. Обчислити висоту і площу трикутника з вершинами в точкахі.

19. Обчислити синус кута між діагоналями паралелограма, побудованого на векторах .

20. Обчислити проекцію вектора на напрям вектора.

21. Знайти об’єм паралелепіпеда, побудованого на векторах .

22. Чи знаходяться точки в одній площині?

23. Знайти об’єм тетраедра, побудованого на векторах , якщо ці вектори направлені за бісектрисами координатних кутів і довжина кожного з них дорівнює 2.

24. Дано піраміду з вершинами і. Обчислити її об’єм і висоту, опущену на граньАВС.

25. Довести, що при будь-яких вектори,компланарні.

26. Дано піраміду з вершинами і. Обчислити її об’єм і висоту, опущену на граньАВС.

27. Обчислити висоту і площу трикутника з вершинами в точкахі.

28. Вектори іутворюють кут, що дорівнює 45. Знайти площу і одну з висот трикутника, побудованого на векторах і, якщо.

29. Дано піраміду з вершинами і. Обчислити її об’єм і висоту, опущену на граньАВС.

30. Обчислити висоту і площу трикутника з вершинами в точкахі.