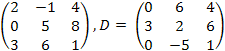- •Науково-методичне видання
- •Рекомендовано науково-методичною радою
- •Вінницького національного аграрного університету
- •Протокол№___від «___»_____________ 2011 р.
- •Лінійна алгебра
- •1.2 Системи лінійних рівнянь та методи їх розв’язків.
- •Розділ 2 Аналітична геометрія
- •2.1. Вектори, типи добутків векторів та методи їх розв’язування.
- •2.2 Пряма на площині
- •2.3. Пряма та площина у просторі
- •Розділ 3 Математичний аналіз
- •I Метод заміни змінної в неозначеному інтегралі.
- •V. Інтегрування тригонометричних функцій.
- •3.5 Означений інтеграл. Формула Ньютона-Лейбніца.
- •I Метод заміни змінної в неозначеному інтегралі.
- •V. Інтегрування тригонометричних функцій.
- •3.5 Означений інтеграл. Формула Ньютона-Лейбніца.
- •Завдання 5
- •Завдання 6
- •Завдання 7
- •Завдання 8
- •Завдання 9
- •Завдання 10
- •Завдання 11
- •Завдання 12
Міністерство аграрної політики України
Вінницький національний аграрний університет
Кафедра вищої математики,інформатики
та математичних методів в економіці
МЕТОДИЧНЕ ЗАБЕЗПЕЧЕННЯ САМОСТІЙНОЇ РОБОТИ СТУДЕНТІВ З ВИЩОЇ МАТЕМАТИКИ
НАВЧАЛЬНО-МЕТОДИЧНИЙ ПОСІБНИК
для студентів всіх спеціальностей ВНАУ
Вінниця-2011
УДК 517
Методичне забезпечення самостійної роботи студентів з вищої математики.Навчально-методичний посібник для студентів всіх спеціальностей /Дубчак В.М.- Вінниця: ВНАУ,2011.-162 c.
Укладач: Дубчак В.М.,к.т.н.,доцент кафедри
вищої математики,інформатики та
математичних методів в економіці
Рецезенти: Михалевич В.М.,д.т.н.,професор,зав.кафедрою
вищої математики ВНТУ,
Джеджула О.М.,д.п.н.,професор кафедри ЗТД
ВНАУ
Коротка анотація
Посібник містить перелік типових стандартних практичних завдань з вищої математики, по кожному з яких пропонується 100 незалежних варіантів,з метою організації самостійної, домашньої, розрахунково-графічної роботи. Матеріали посібника можуть бути використані для організації роботи студентів всіх спеціальностей університету,які вивчають основи вищої математики.
Науково-методичне видання
Рекомендовано науково-методичною радою
Вінницького національного аграрного університету
Протокол№___від «___»_____________ 2011 р.
ЗМІСТ
Вступ 4
Короткий теоретичний курс 5
Модуль 1
1.Системи алгебраїчних рівнянь,методи їх розв’язку 58
2.Вектори,типи добутку векторів 70
3.Пряма на площині 83
4.Площина в просторі 84
Модуль 2
5.Границі функцій,розкриття неозначених границь 90
6.Похідні функцій,їх обчислення 123
Модуль 3
7.Дослідження функцій і побудова їх графіків методами 142 диференціального числення
8.Неозначений інтеграл,методи інтегрування функцій 147
Література 162
ВСТУП
Навчальний посібник призначений для організації самостійної,домашньої,розрахунково-графічної роботи студентів всіх спеціальностей,в навчальній програмі яких присутні початкові розділи вищої математики,такі як лінійна алгебра,аналітична геометрія,теорія неозначених границь,основи диференціального та інтегрального числення. В роботі приведені короткі теоретичні матеріали,а по кожному із наведених завдань пропонується по 100 незалежних варіантів для організації самостійного розв’язку. В кінці роботи приведено перелік рекомендованої літератури для виконання даних завдань.
Розділ 1
Лінійна алгебра
Матриці. Дії над матрицями. Визначники.
Матрицею розмірів m x n називається прямокутна таблиця чисел, які розташовані в m рядках і n стовпцях та називаються елементами матриці.

де aij – елементи матриці, i – номер рядка, j – номер стовпця
Множення матриці на число:
λ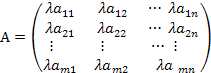
Сума (різниця) двох матриць:
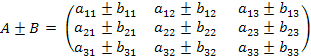
* Дана дія виконується тільки для матриць однакової розмірності.
Добуток двох матриць:
C
= A·B
=  ,
де
,
де ![]()
* Дана дія можлива тільки при умові, якщо кількість рядків першої матриці відповідає кількості стовпцям другої матриці.
Транспонування матриці:
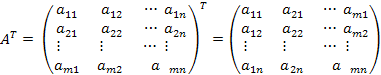
Визначник матриці другого порядку:
![]() =
= ![]()
Визначник матриці третього порядку (правило трикутників):
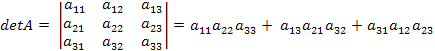 −
−
![]()
Теорема розкладання:
Якщо А – квадратна матриця, то її визначник дорівнює сумі добутків елементів будь – якого стовпця (рядка) на їх алгебраїчне доповнення.
*Теорема розкладу дає можливість обчислювати визначники вищих порядків.
Обернена матриця:
Матриця
А–1
називається оберненою матрицею до
квадратної невиродженої матриці А,
якщо виконується співвідношення:
![]() .
.
Обернена матриця має вигляд:
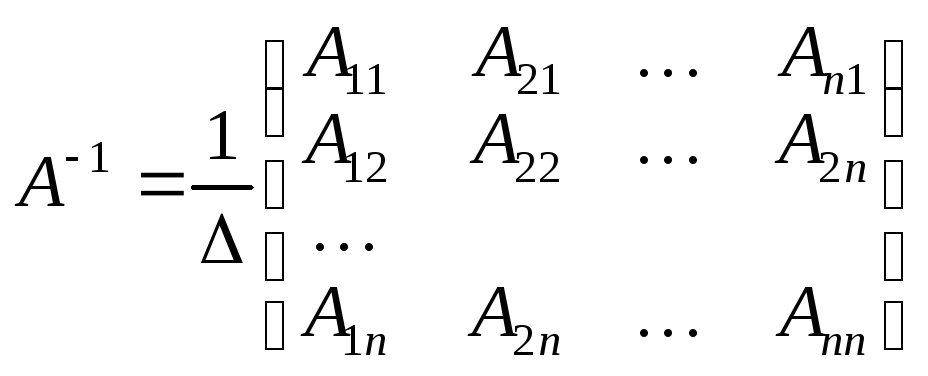 .
.
Приклад 1
Знайти
значення виразу Y=
-3A
+BT,
де А=![]() ;
В=
;
В=![]()
Розв’язок.
![]() .
.
Приклад 2
Знайти добуток двох матриць С·D, де
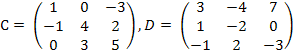
Розв’язок.

Приклад 3
Знайти: detA, det D.
Розв’язок.
![]()
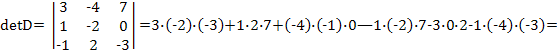
![]()
Приклад 4
Знайти
матрицю, обернену до матриці
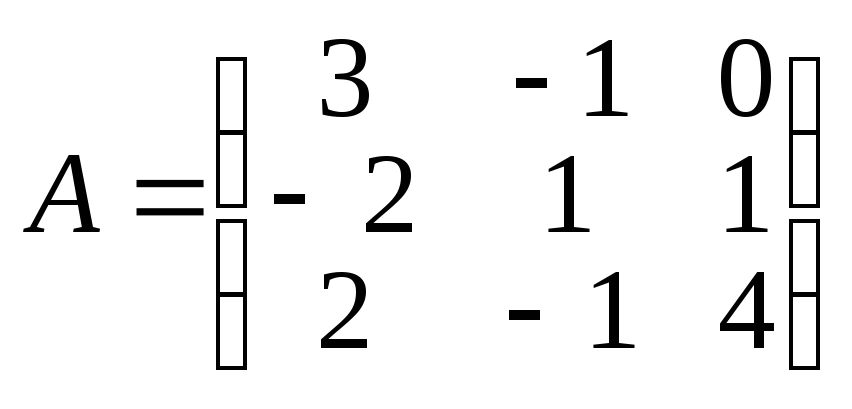 .
.
Розвязок.
Обчислимо:
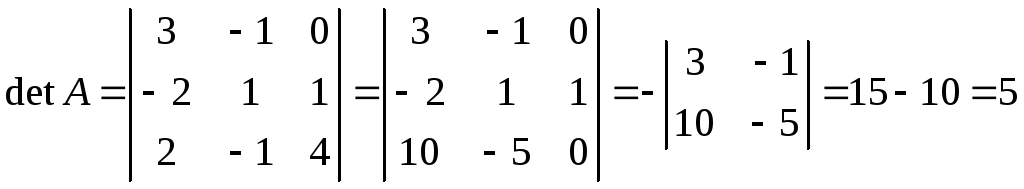 .
.
![]() — обернена матриця існує.
— обернена матриця існує.
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
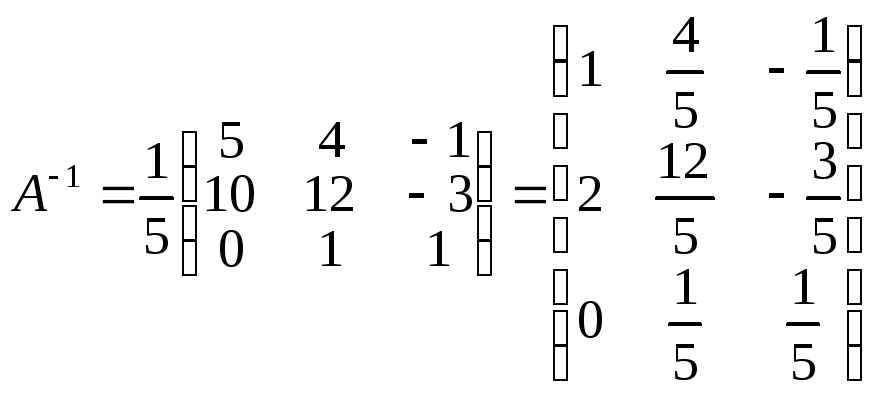 .
.
Переконаємося,
що матриця А–1,
побудована
нами, справді є оберненою до матриці А.
Знайдемо
![]() :
:
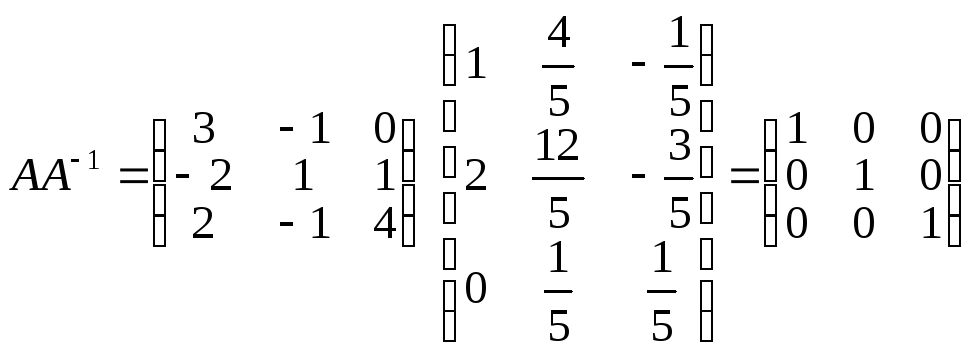 .
.
Завдання 1.
Знайти значення виразу:
Х = АТ – 4В
Знайти добуток двох матриць: D·C
Знайти detA, debB, detC, detD.
(detC, detD визначити двома способами:
методом трикутників та за теоремою розкладу)
Знайти обернені матриці А-1, В-1, С-1, D-1 та зробити перевірку.
Варіанти завдань для самостійного виконання.
1.
![]() ,
C
=
,
C
= 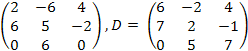
2.
![]() ,
C
=
,
C
= 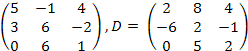
3.
![]() ,
C
=
,
C
= 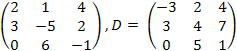
4.
![]() ,
C
=
,
C
= 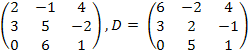
5.
![]() ,
C
=
,
C
= 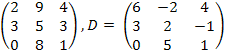
6.![]() ,
C
=
,
C
= 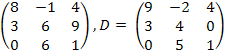
7.![]() ,
C
=
,
C
= 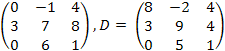
8.
![]() ,
C
=
,
C
= 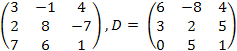
9.
![]() ,
C
=
,
C
= 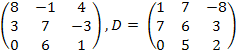
10.
![]() ,
C
=
,
C
= 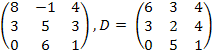
11.
![]() ,
C
=
,
C
= 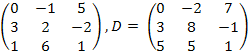
12.
![]() ,
C
=
,
C
= 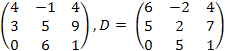
13.
![]() ,
C
=
,
C
= 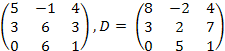
14.
![]() ,
C
=
,
C
= 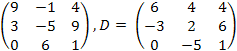
15.
![]() ,
C
=
,
C
= 
16.
![]() ,
C
=
,
C
= 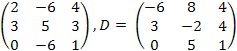
17.
![]() ,
C
=
,
C
= 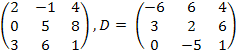
18![]() ,
C
=
,
C
= 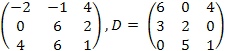
19.
![]() ,
C
=
,
C
= 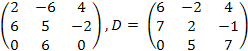
20.
![]() ,
C
=
,
C
= 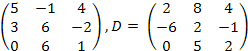
21.
![]() ,
C
=
,
C
= 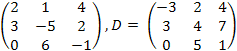
22.
![]() ,
C
=
,
C
= 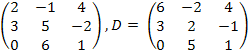
23.
![]() ,
C
=
,
C
= 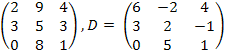
24.![]() ,
C
=
,
C
= 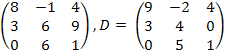
25.![]() ,
C
=
,
C
= 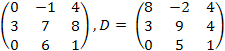
26.
![]() ,
C
=
,
C
= 
27.
![]() ,
C
=
,
C
= 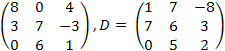
28.
![]() ,
C
=
,
C
= 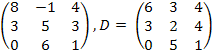
29.
![]() ,
C
=
,
C
= 
30.
![]() ,
C
=
,
C
=