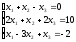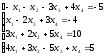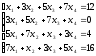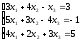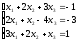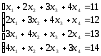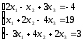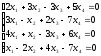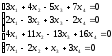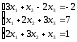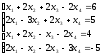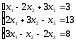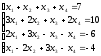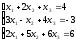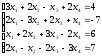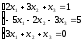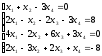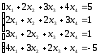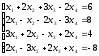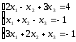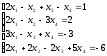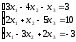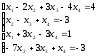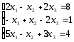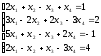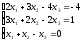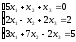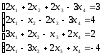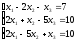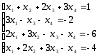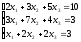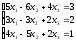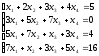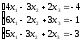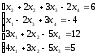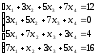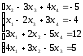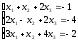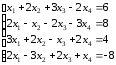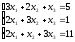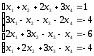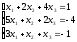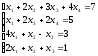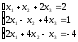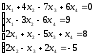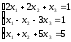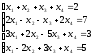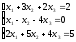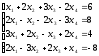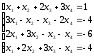Математика
.docxМЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕРЫ
ВЫПОЛНЕНИЯ ЗАДАНИЙ
Пример 1 (Метод Крамера):
С помощью определителей решить систему уравнений
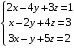
Решение: Найдем определитель системы
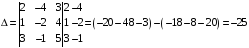 .
.
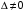 – система
имеет единственное решение.
– система
имеет единственное решение.
Дополнительные определители получают, заменив столбец коэффициентов при неизвестном свободными членами.
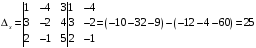 ,
,
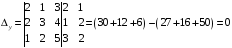
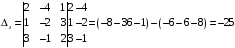 .
.
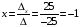 ;
;
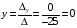 ;
;
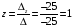 .
.
Ответ: (-1;0;1)
Пример 2 (Метод Гаусса): Решить систему уравнений методом последовательного исключения неизвестных.
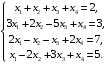
Решение:
Стрелочками укажем действия над данной строкой уравнения и место записи результата этого действия
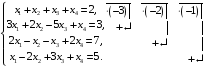


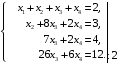
Разделим
последнюю и предпоследнюю строки на 2;
поменяем столбцы при
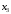 и
и
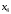 .
.
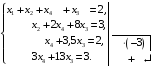


Ответ:
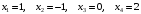
Пример 3: Решить систему уравнений средствами матричного исчисления.
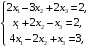
Решение:
Представим
систему в матричном виде:
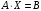 ,
где
,
где
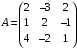 ,
,
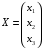 ,
,
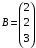
Тогда
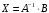 .
Это матичная запись решения системы
линейных уравнений. Таким образом, чтобы
решить систему линейных уравнений надо:
.
Это матичная запись решения системы
линейных уравнений. Таким образом, чтобы
решить систему линейных уравнений надо:
-
составить матрицу
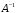 ,
обратную матрицы системы
,
обратную матрицы системы
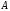 ;
; -
умножить матрицу
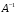 слева на матрицу-столбец свободных
членов
слева на матрицу-столбец свободных
членов
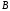 ;
;
В результате этого мы получим столбец – решение системы.
Составим обратную матрицу для матрицы A.
1.
Существует ли для матрицы
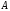 обратная матрица
обратная матрица
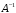 ?
?
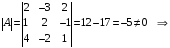
матрица
 невырожденная (
невырожденная (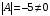 ),
следовательно, обратная матрица
),
следовательно, обратная матрица
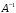 существует.
существует.
2.
Для нахождения транспонированной
матрицы алгебраических дополнений
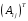 счет элементов
счет элементов
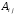 будем вести в том порядке, как это
указанно в формуле
будем вести в том порядке, как это
указанно в формуле
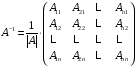 .
.
 ,
,
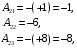 ,
,
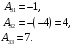
Получим:
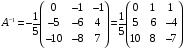 -
обратная матрица.
-
обратная матрица.
Применив
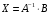 ,
получим
,
получим
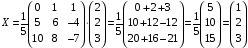
Ответ:
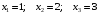 .
.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
а). Решить систему уравнений методом Крамера и с помощью обратной матрицы.
б). Решить систему уравнений методом Гаусса.
|
1.
а)
|
б)
|
|
2.
а)
|
б) |
|
3.
а)
|
б) |
|
4.
а)
|
б) |
|
5.
а)
|
б) |
|
6.
а)
|
б) |
|
7.
а) |
б) |
|
8.
а)
|
б) |
|
9.
а) |
б) |
|
10.
а) |
б) |
|
11.
а)
|
б) |
|
12.
а)
|
б) |
|
13.
а) |
б) |
|
14.
а) |
б) |
|
15.
а)
|
б) |
|
16.
а)
|
б) |
|
17.
а) |
б) |
|
18.
а)
|
б) |
|
19.
а) |
б) |
|
20.
а) |
б) |
|
21.
а) |
б) |
|
22.
а)
|
б) |
|
23.
а) |
б) |
|
24.
а) |
б) |
|
25.
а)
|
б) |
|
26.
а) |
б) |
|
27.
а) |
б) |
|
28.
а) |
б) |
|
29.
а) |
б) |
|
30.
а)
|
б) |