4. Прямая и плоскость в пространстве

Основные виды уравнений плоскости.

1) -общее уравнение плоскости ;

2) - уравнение плоскости, проходящей через точкуМ₁( x₁, y₁, z₁ ) перпендикулярно нормальному вектору ;

3) -уравнение плоскости в отрезках, где а, b, с - величины отрезков, отсекаемых плоскостью на координатных осях Ох ,Оy, Оz соответственно ;

4) 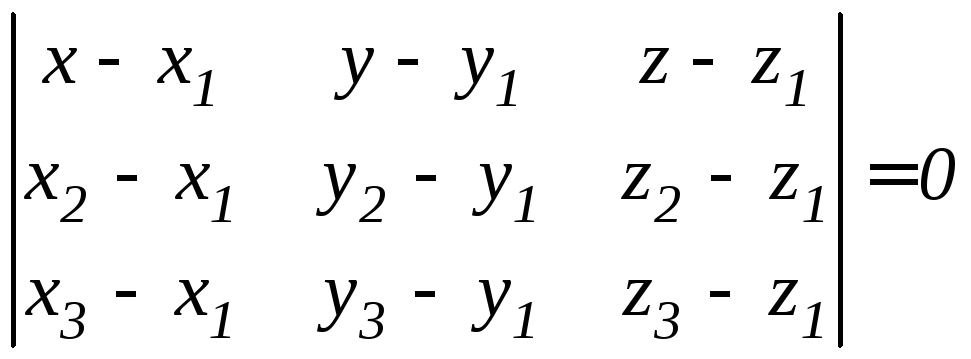-уравнение плоскости, проходящей через три точки М₁( x₁, y₁, z₁ ) , М₂( x₂, y₂, z₂ ) , М₃( x₃, y₃, z₃ ).

Основные виды уравнений прямой.

1) -общее уравнение прямой, как пересечение двух плоскостей , где направляющий вектор прямой находится из векторного произведения нормальных векторов плоскостей

;

2) -каноническое уравнение прямой или уравнение прямой , проходящей через точку М₁( x₁, y₁, z₁ ) параллельно вектору ;.

3) - уравнение прямой, проходящей через две точки М₁( x₁, y₁, z₁ ) и М₂( x₂, y₂, z₂ );

4) -векторное уравнение прямой, где - радиус-вектор точки, лежащей на прямой,- направляющий вектор прямой, или в параметрической форме.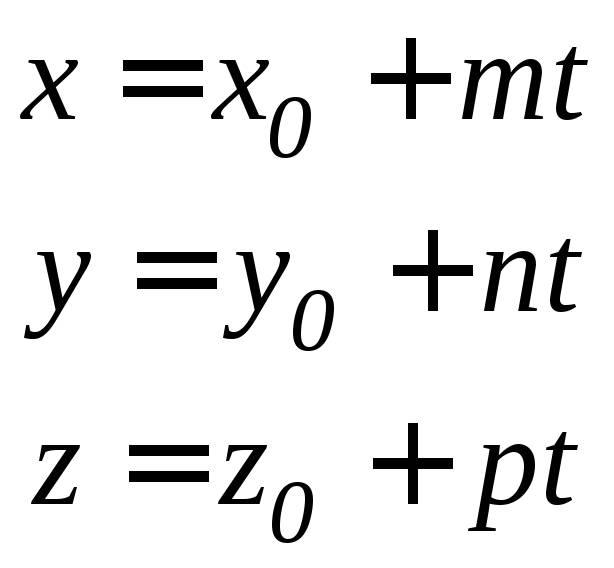

Расстояние от точки до плоскости определяется по формуле.

Угол между двумя прямыми, заданными в канонической форме 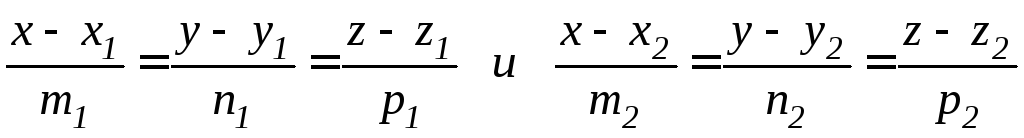, определяется как угол между их направляющими векторами

.

Угол между прямой и плоскостью определяется так :

.

Задача. Составить уравнение прямой, проходящей через точку А(1,2,3) параллельно прямой .

Решение. Так как прямые параллельны, значит направляющий вектор для искомой прямой будет таким же, как и для данной, т.е. . Поэтому применяем каноническое уравнение прямой, проходящей через точкуА (1,2,3) параллельно вектору , т.е..

Задача. Составить уравнение прямой, проходящей через точку А(2,-3,5) параллельно прямой, заданной в виде пересечения двух плоскостей: .

Решение. Найдем направляющий вектор заданной прямой через векторное произведение нормальных векторов плоскостей

.

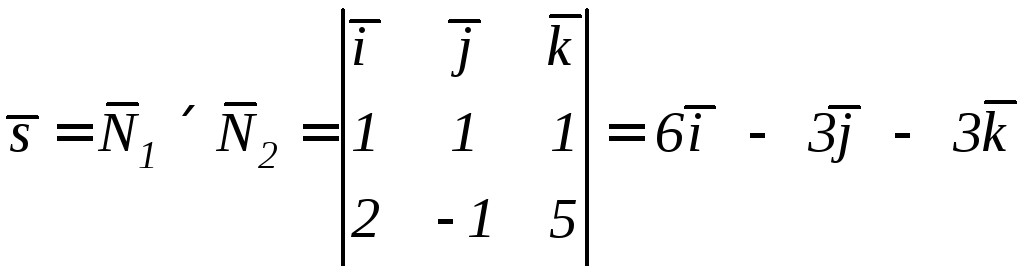Тогда каноническое уравнение прямой, проходящей через точку А(2,-3,5) параллельно вектору будет.

Задача. Дана пирамида АВСD с вершинами А(1,5,7), В(-1,0,1), С ( 3,-2,4 ), D ( 0,1,-1 ). Найти угол между ребром АD и гранью АВС .

Решение. Найдем уравнение грани АВС , т.е. уравнение плоскости, проходящей через три точки А , В и С .

Уравнение ребра AD - уравнение прямой, проходящей через две точки А и D :

.

Тогда угол между ребром и гранью будем находить по формуле угла между прямой и плоскостью:

.

Задача. Составить уравнение плоскости, проходящей через точку А(1,2,3) и через прямую, данную в виде пересечения двух плоскостей

.

Решение. Воспользуемся уравнением пучка плоскостей, проходящих через данную прямую . Так как плоскость должна проходить через точкуА, то, подставив ее координаты в уравнение пучка, найдем λ :

.

Теперь, подставив λ в уравнение пучка, получим искомую плоскость:

Задача. Найти точку пересечения прямой и плоскости .

Решение. Параметрически уравнения прямой запишутся в виде . Далее, подставив в уравнение плоскости, найдемt : .

По данному t найдем координаты точки пересечения

.

Задание 4.1.

Даны координаты вершин пирамиды АВСD. Найти:

1) Уравнение грани АВС;

2) Уравнение высоты DM, опущенной из точки D на грань АВС;

3) Длину высоты ДМ;

4) Уравнение ребра DC;

5) Угол наклона ребра DC к плоскости АВС.

1. А(-3;-2;-4), B(-4;2;-7), C(5;0;3), D(-1;3;0)

2. A(2;-2;1), B(-3;0;-5), C(0;-2;-1), D(-3;4;2)

3. A(5;4;1), B(-1;-2;-2), C(3;-2;2), D(-5;5;4)

4. A(3;6;-2), B(0;2;-3), C(1;-2;0), D(-7;6;6)

5. A(1;-4;1), B(4;4;0), C(-1;2;-4), D(-9;7;8)

6. A(4;6;-1), B(7;2;4), C(-2;0;-4), D(3;1;-4)

7. A(0;6;-5), B(8;2;5), C(2;6;-3), D(5;0;-6)

8. A(-2;4;-6), B(0;-6;1), C(4;2;1), D(7;-1;-8)

9. A(-4;-2;-5), B(1;8;-5), C(0;4;-4), D(9;-2;-10)

10. A(3;4;-1), B(2;-4;2), C(5;6;0), D(11;-3;-12)

11. A(2;1;3), B(3;-2;-4), C(-1;-3;-2), D(5;-3;4)

12. A(4;1;1), B(-2;-1;3), C(1;-3;-4), D(6;-5;5)

13. A(-3;-2;2), B(0;1;5), C(1;-2;-2), D(-1;9;-2)

14. A(-1;0;4), B(2;2;5), C(3;2;4), D(2;3;1)

15. A(-2;0;5), B(1;-4;-6), C(3;2;4), D(2;3;1)

16. A(2;1;-1), B(0;3;-1), C(5;2;1), D(-2;-1;5)

17. A(2;3;0), B(3;4;1), C(-2;5;-1), D(3;4;-5)

18. A(-3;0;-4), B(2;7;2), C(4;-1;-1), D(-3;-2;7)

19. A(1;-4;-4), B(-1;0;-3), C(2;5;1), D(5;6;-9)

20. A(3;2;0), B(5;-2;-1), C(-4;3;-3), D(2;3;-3)

21. A(1;1;1), B(6;3;2), C(0;7;1), D(2;3;4)

22. A(1;0;-1), B(5;1;1), C(2;6;1), D(3;4;5)

23. A(-1;2;0), B(8;1;1), C(2;7;-1), D(4;3;6)

24. A(-1;-1;0), B(9;2;1), C(0;8;-1), D(4;4;7)

25. A(0;1;0), B(8;2;1), C(1;7;2), D(3;5;1)

Задание 4.2.

Даны координаты точек А, В, С. Требуется:

1) составить каноническое уравнение прямой АВ;

2) составить уравнение прямой, проходящей через точку С параллельно прямой АВ;

3) составить уравнение плоскости, проходящей через точку С перпендикулярно прямой АВ;

4) найти следы этой плоскости на координатных плоскостях.

1. A(3;-1;5), B(7;1;1), C(4;-2;1). 2. A(-1;2;3), B(3;4;-1), C(0;1;-1).

3. A(2;-3;7), B(6;-1;3), C(3;-4;3). 4. A(0;-2;6), B(4;0;2), C(1;-3;2).

5. A(-3;1;2), B(1;3;-2), C(-2;0;-2). 6. A(-2;3;1), B(2;5;-3), C(-1;2;-3).

7. A(-4;0;8), B(0;2;4), C(-3;-1;4). 8. A(1;4;0), B(5;6;-4), C(2;3;-4).

9. A(4;-4;9), B(8;-2;5), C(5;-5;5). 10. A(5;5;4), B(9;7;0), C(6;4;0).

11. A(3;0;4), B(5;2;6), C(2;3;-3). 12. A(3;-2;2), B(-3;1;2), C(-1;2;1).

13. A(1;-1;1), B(-2;1;3), C(4;-5;-2). 14. A(3;-1;2), B(4;-1;-1), C(2;0;2).

15. A(-1;2;1), B(-3;1;2), C(3;-2;2). 16. A(9;-11;5), B(7;4;2), C(-7;13;-3).

17. A(2;4;-1), B(2;-4;2), C(3;6;0). 18. A(-4;-2;-5), B(1;8;-5), C(0;4;-4).

19. A(-2;4;-6), B(0;-6;1), C(4;2;1). 20. A(4;6;-1), B(7;2;4), C(-2;0;-4).

21. A(3;3;0), B(-1;2;-4), C(-9;7;8). 22. A(7;2;4), B(-2;0-4), C(3;1;-4).

23. A(8;2;5), B(2;6;-3), C(5;0;-6). 24. A(0;-6;1), B(4;2;1), C(7;-1;-8).

25. A(1;8;-5), B(0;4;-4), C(9;-2;-10).

Задание 4.3.

Даны уравнение прямой в виде пересечения двух плоскостей и координаты точки А. Требуется:

1) составить уравнение плоскости, проходящей через данную прямую и точку А;

2) составить каноническое уравнение прямой, проходящей через точку А и параллельно оси ОX;

3) найти угол между полученной прямой и плоскостью;

4) найти расстояние от начала координат до плоскости.

1. 2x-y-3z=-1 A(3;0;2)

x+5y+z=0

2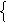. x+2y+3z=1 A(1;2;0)

2x-3y+2z=9

3. x+y - z=1 A(-1;2;1)

8x+3y-6z=2

4. x+y-z=-2 A(2;-3;0)

4x-3y+z=1

5. 2x+5y-3z=4 A(0;4;-2)

4x-3y+2z=9

6. 2x+7y-z=8 A(-3;0;5)

x+2y+z=4

7. 3x+4y+2z=8 A(1;3;0)

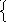x+5y+z=0

8. x-4y-2z=-3 A(5;1;-2)

3x+y+z=5

9. x+y-z=1 A(-2;0;1)

x+2y+z=4

1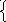0. 3x+y+z=5 A(0;-5;2)

4x-3y+z=1

11. x+4y-5z=-1 A(2;-1;2)

2x-y+3z=-2

12. x+y-2z=-1 A(2;0;-1)

3x-y+z=2

13. 2x-y+z=3 A(1;1;-2)

2x+4y-z=4

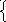
14. x+2y-3z=1 A(0;2;1)

2x-y+2z=-2

15. 3x-y+z=-2 A(1;-1;2)

x+2y-z=1

16. 2x-y+3z=6 A(1;2;4)

x+2y-z=-3

17. 3x+y+z=4 A(1;3;2)

x +3z=5

18. 3x+2y-5z=4 A(2;1;2)

x-2y+3z=4

19. 3x-5y+z=8 A(-1;2;3)

2x+y-z=-2

20. 2x-3y-3z=9 A(2;-5;3)

x-2y+z=-3

21. x+y+z=3 A(1;1;7)

2x-3y+z=5

22. x-y+2z=4 A(1;2;1)

2x+y+z=3

23. x+y+2z=5 A(1;1;1)

3x+y+3z=-2

24. x+2y-3z=3 A(1;2;0)

x+3y+z=2

25. x+y+z=1 A(0;1;2)

x-3y+2z=10

31