
- •Определители и матрицы. Системы линейных уравнений
- •1.1. Матрицы и определители
- •1.2. Решение систем линейных уравнений
- •Последней матрице соответствует ступенчатая система уравнений , равносильная данной. Неизвестныеxи y можно выразить через z:
- •2. Векторы и операции над векторами
- •Скалярное произведение векторов. Скалярным произведением векторов иназывается число.
- •3. Прямая на плоскости
- •Координаты точки м(X, y), которая делит отрезок между точкамиМ1(x1,y1) иМ2(x2,y2) в отношенииλ , находятся по формулам
- •Основные виды уравнений прямой на плоскости.
- •4. Прямая и плоскость в пространстве
- •Решение. Найдем направляющий вектор заданной прямой через векторное произведение нормальных векторов плоскостей
2. Векторы и операции над векторами
В ектором
называется направленный отрезок в
пространстве, имеющий определенную
длину.
ектором
называется направленный отрезок в
пространстве, имеющий определенную
длину.
Обозначают
![]() или
или![]() .
Длина вектора - модуль,
.
Длина вектора - модуль,
обозначают
![]() ,
,![]() .
.
Нуль-вектор
-
![]() - вектор, не имеющий определенного
направления, и модуль
- вектор, не имеющий определенного
направления, и модуль![]() .
.
Вектора, расположенные на одной или параллельных прямых, называются коллинеарными.
Вектор
(-![]() )
называютпротивоположным
вектору
)
называютпротивоположным
вектору
![]() , он коллинеарен вектору
, он коллинеарен вектору![]() и направлен в противоположную сторону.
и направлен в противоположную сторону.
Сложение:
по правилу треугольника; по правилу параллелограмма.
![]()


![]()
![]() +
+![]()
![]()
![]() +
+![]()
![]()
Вычитание:
![]() -
-![]()
![]()
-![]()
![]()
Произведением
вектора
![]() на число
на число![]() называется вектор
называется вектор![]() , модуль которого
, модуль которого![]() , и направление совпадает с направлением
, и направление совпадает с направлением![]() ,
если
,
если![]() ,
и противоположно, если
,
и противоположно, если![]() .
.
Вектора, лежащие на одной или параллельных плоскостях называются компланарными .
Система
векторов
![]() называетсялинейно
зависимой,
если существуют числа λ1,
λ2
, … ,
λn
такие,
что хотя бы одно из них отлично от нуля
и
называетсялинейно
зависимой,
если существуют числа λ1,
λ2
, … ,
λn
такие,
что хотя бы одно из них отлично от нуля
и
![]() .
В противном случае система называетсялинейно
независимой
.
.
В противном случае система называетсялинейно
независимой
.
Максимальное число линейно независимых векторов в пространстве называется базисом .
Вектора
![]() - попарно перпендикулярны и, имеющие
единичную длину, обозначают прямоугольный
декартов базис. Всякий вектор
- попарно перпендикулярны и, имеющие
единичную длину, обозначают прямоугольный
декартов базис. Всякий вектор![]() может быть единственным образом
представлен как
может быть единственным образом
представлен как
![]() ,
где
,
где
![]() -
называются координатами вектора в
базисе (
-
называются координатами вектора в
базисе (![]() )
и представляют собой проекции вектора
)
и представляют собой проекции вектора![]() на осиx,
y,
z
.
на осиx,
y,
z
.

аz
![]()
![]()
![]() ay
ay
![]()
ax
Скалярное произведение векторов. Скалярным произведением векторов иназывается число.
Если
вектора заданы координатами
![]() ,
,![]() ,
то скалярное произведение
,
то скалярное произведение![]() .
.
Из формулы нахождения скалярного произведения можно находить косинус угла между двумя векторами
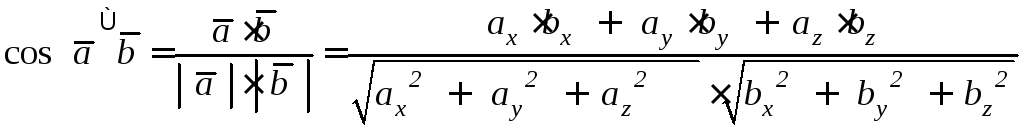 .
.
Векторное
произведение векторов.
Векторным произведением двух векторов
![]() и
и![]() называется вектор
называется вектор![]() , определяемый тремя условиями :
, определяемый тремя условиями :
модуль вектора
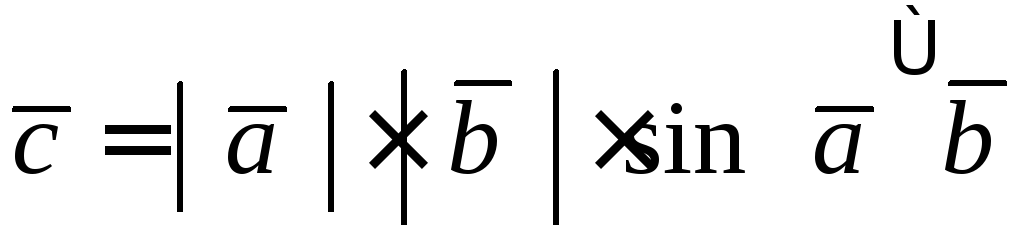 численно равен площади параллелограмма
, построенного на векторах
численно равен площади параллелограмма
, построенного на векторах и
и , как на сторонах;
, как на сторонах;вектор
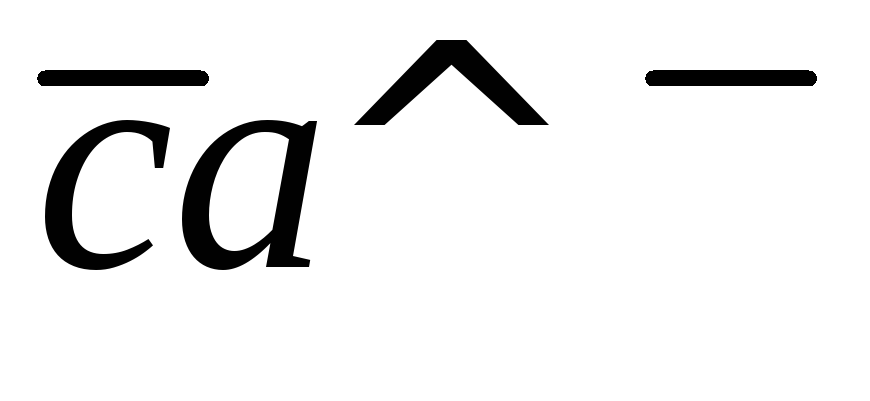 и
и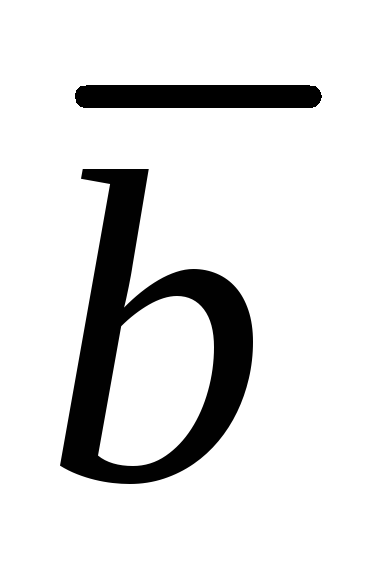 ;
;вектора
 образуют правую тройку, т. е. если
смотреть с конца вектора
образуют правую тройку, т. е. если
смотреть с конца вектора на вектора
на вектора и
и , то поворот от вектора
, то поворот от вектора к
к по кратчайшему расстоянию виден
совершающимся против часовой стрелки.
по кратчайшему расстоянию виден
совершающимся против часовой стрелки.

![]()
![]()
![]()
![]()
![]()
![]()
Если
вектора
![]() и
и![]() заданы координатами
заданы координатами![]() ,
,
![]() ,
то векторное произведение находится
так
,
то векторное произведение находится
так

![]()
Пример. Найти площадь треугольника с вершинами
А ( 1,1,1 ), В ( 2,5,7 ), С ( 3,2,4 ) .
Решение.
Рассмотрим вектора
![]() .
.
Найдем их векторное произведение
 .
.
Модуль
векторного произведения векторов
численно равен площади параллелограмма,
построенного на векторах
![]() , как на сторонах
, как на сторонах
![]() .
.
Тогда
площадь ΔАВС
будет равна
половине площади параллелограмма SΔ
=![]() .
.
Смешанное
произведение
. Смешанным
произведением трех векторов
![]() называется число, равное векторно-скалярному
произведению векторов
называется число, равное векторно-скалярному
произведению векторов![]() .
Геометрически смешанное произведение
с точностью до знака численно равно
объему параллелепипеда, построенного
на векторах
.
Геометрически смешанное произведение
с точностью до знака численно равно
объему параллелепипеда, построенного
на векторах![]() , как на ребрах.Смешанное
произведение через координаты векторов
выражается в виде
, как на ребрах.Смешанное
произведение через координаты векторов
выражается в виде
 .
.
Если
три вектора
![]() компланарны, то их смешанное произведение
компланарны, то их смешанное произведение![]() =0
и наоборот.
=0
и наоборот.
Пример. Найти объем тетраэдра с вершинами
А ( 2,-3,5 ), В ( 0,2,1 ), С ( -2,-2,3 ), D( 3,2,4 ).
Решение. Рассмотрим три вектора :
![]() .
.
Найдем смешанное произведение этих векторов:

Объем
тетраэдра равен
![]() объема параллелепипеда, тогда
объема параллелепипеда, тогда
VABCD
=
![]() .
.
Задание 2.1.
1.
Дан равносторонний треугольник АВС.
Найти построением векторы
![]()
![]() .
.
В треугольнике ОАВ проведена медиана ОС. Доказать, что
 .
.
3.
При каких значениях α
и β
векторы
![]() и
и![]() коллинеарны ?
коллинеарны ?
4.
По данным векторам
![]() и
и![]() построить каждый из следующих:
построить каждый из следующих:![]() .
.
5.
Заданы векторы
![]() ,
,![]() ,
,![]() . Найти : координаты вектора
. Найти : координаты вектора![]() ; разложение вектора
; разложение вектора![]() по базису (
по базису (![]() )
.
)
.
6.
Дан треугольник АВС
. На стороне
ВС
расположена точка М
так, что
![]() . Найти
. Найти![]() ,
если
,
если![]() .
.
7.
В трапеции ABCD
![]() . Выразить
. Выразить![]() через
через
![]() .
.
8.
Вне плоскости треугольника АВС
взята точка О
. Построить векторы
![]() .
.
9.
ABCD
- параллелограмм, О
- точка пересечения его диагоналей.
Выразить через
![]() векторы
векторы![]() .
.
10.
По сторонам ОА
и ОВ
прямоугольника ОАСВ
отложены единичные векторы
![]() и
и![]() . Выразить через
. Выразить через![]() и
и![]() векторы
векторы![]() .
.
Выразить векторы–медианы треугольника АВС через два вектора
 - стороны его.
- стороны его.
12.
ABCD-
параллелограмм, О
- точка пересечения его диагоналей ,
![]() .
Выразить через
.
Выразить через![]() векторы
векторы![]() .
.
13.
ABCD
- параллелограмм,
![]() . Выразить через
. Выразить через![]() и
и![]() векторы
векторы![]() , гдеМ
- точка пересечения диагоналей.
, гдеМ
- точка пересечения диагоналей.
14.
ABCD
- параллелограмм, О
- точка пересечения его диагоналей .
Выразить через
![]() векторы
векторы![]() .
.
15.
В треугольнике АВС
сторона АВ
точками
М
и Р
разделена на три части так, что
![]() . Найти вектор
. Найти вектор![]() ,
если
,
если![]() .
.
16.
ABCDA1B1C1D1
-
параллелепипед с основанием ABCD
. Выразить векторы ВD1
и
DВ1
через
![]() .
.
17.
В правильной четырехугольной пирамиде
SABCD
( S
- вершина ). Выразить через
![]() векторы , совпадающие с остальными
ребрами пирамиды.
векторы , совпадающие с остальными
ребрами пирамиды.
18.
На основании
![]() треугольникаОАВ
отложен отрезок
треугольникаОАВ
отложен отрезок
![]() . Выразить вектор
. Выразить вектор![]() через векторы
через векторы![]() .
.
19.
В прямой треугольной призме АВСА1В1С1
дано:
![]() . Выразить через
. Выразить через![]() векторы, совпадающие с ребрами этой
призмы.
векторы, совпадающие с ребрами этой
призмы.
20.
Основание АВ
треугольника разделено точкой М
в соотношении 2
: 3 . Выразить
вектор
![]() через
через![]() .
.
21.
Треугольник АВС
построен
на векторах
![]() и
и![]() так, что
так, что![]() .
Выразить через
.
Выразить через![]() и
и![]() векторы
векторы![]() ,
совпадающие с медианами данного
треугольника.
,
совпадающие с медианами данного
треугольника.
22.
В ромбе АВСD
даны диагонали
![]() .
Разложить по этим векторам все векторы
, совпадающие со сторонами ромба :
.
Разложить по этим векторам все векторы
, совпадающие со сторонами ромба :![]() .
.
23.
![]() -
медианы треугольникаАВС
. Доказать
равенство
-
медианы треугольникаАВС
. Доказать
равенство
![]() .
.
24.
Заданы векторы
![]() . Найти координаты вектора
. Найти координаты вектора![]() .
.
25.
Заданы векторы
![]() . Найти координаты вектора
. Найти координаты вектора![]() .
.
26.
Дан вектор
![]() . Найти вектор
. Найти вектор![]() , если
, если![]() .
.
27.
Найти длину вектора
![]() .
.
28.
М
– точка пересечения медиан треугольника
АВС
, О
- произвольная точка пространства.
Доказать равенство
![]() .
.
29.
Даны векторы
![]() и
и![]() .
Проверить следующую формулу
.
Проверить следующую формулу![]() .
.
Проверить на рисунке следующие формулы :
 .
.
Задание 2.2.
Даны координаты вершин пирамиды ABCD . Требуется :
1)
найти векторы
![]() и
их модули ;
и
их модули ;
2)
найти угол между векторами
![]() ;
;
3) найти площадь грани АВС ;
4) найти объем пирамиды .
А ( 2,-3,1 ) , В ( 6,1,-1 ) , С ( 4,8,-9 ) , D ( 2,-1,2 ).
А ( 5,-1,-4 ) , В ( 9,3,-6 ) , С ( 7,10,-14 ) , D ( 5,1,-3 ).
А ( 1,-4,0 ) , В ( 5,0,-2 ) , С ( 3,7,-10 ) , D ( 1,-2,1 ).
А ( -3,-6,2 ) , В ( 1,-2,0 ) , С ( -1,5,-8 ) , D ( -3,-4,3 ).
А ( -1,1,-5 ) , В ( 3,5,-7 ) , С ( 1,12,-15 ) , D ( -1,3,-4 ).
А ( -4,2,-1 ) , В ( 0,6,-3 ) , С ( -2,13,-11 ) , D ( -4,4,0 ).
А ( 0,4,3 ) , В ( 4,8,1 ) , С ( 2,15,-7 ) , D ( 0,6,4 ).
А ( -2,0,-2 ) , В ( 2,4,-4 ) , С ( 0,11,-12 ) , D ( -2,2,-1 ).
А ( 3,3,-3 ) , В ( 7,7,-5 ) , С ( 5,14,-13 ) , D ( 3,5,-2 ).
А ( 4,-2,5 ) , В ( 8,2,3 ) , С ( 6,9,-5 ) , D ( 4,0,6 ).
А ( -5,0,1 ) , В ( -4,-2,3 ) , С ( 6,2,11 ) , D ( 3,4,9 ).
А ( 1,-4,0 ) , В ( 2,-6,2 ) , С ( 12,-2,10 ) , D ( 9,0,8 ).
А ( -1,-2,-8 ) , В ( 0,-4,-6 ) , С ( 10,0,2 ) , D ( 7,2,0 ).
А ( 0,2,-10 ) , В ( 1,0,-8 ) , С ( 11,4,0 ) , D ( 8,6,-2 ).
А ( 3,1,-2 ) , В ( 4,-1,0 ) , С ( 14,3,8 ) , D ( 0,7,7 ).
А ( 8,3,-1 ) , В ( -7,1,1 ) , С ( 3,5,9 ) , D ( 0,7,7 ).
А ( 2,-1,-4 ) , В ( 3,-3,-2 ) , С ( 13,1,6 ) , D ( 10,3,4 ).
А ( 4,5,-5 ) , В ( -3,3,-3 ) , С ( 7,7,5 ) , D ( 4,9,3 ).
А ( -2,-3,2 ) , В ( -1,-5,4 ) , С ( 9,-1,12 ) , D ( 6,1,10 ).
А ( -3,4,-3 ) , В ( -2,2,-1 ) , С ( 8,6,7 ) , D ( 5,8,5 ).
А ( 3,2,-6 ) , В ( 0,-5,1 ) , С ( -2,1,0 ) , D ( 4,-1,3 ).
А ( 4,-1,0 ) , В ( -1,2,-3 ) , С ( 2,1,-2 ) , D ( 3,4,5 ).
А ( -3,6,3 ) , В ( 1,5,-7 ) , С ( -2,7,3 ) , D ( 1,-1,2 ).
А ( 1,1,-1 ) , В ( 2,3,1 ) , С ( 3,2,1 ) , D ( -3,-7,6 ).
А ( 2,3,1 ) , В ( 4,1,-2 ) , С ( 6,3,7 ) , D ( -5,-4,8 ).
А ( 2,3,8 ) , В ( 2,-2,4 ) , С ( -1,1,3 ) , D ( 1,1,2 ).
А ( 2,-1,2 ) , В ( 1,2,-1 ) , С ( 3,2,1 ) , D ( -5,3,7 ).
А ( -13,-8,16 ) , В ( 5,2,6 ) , С ( 3,0,-3 ) , D ( 1,2,0 ).
А ( 14,4,5 ) , В ( -5,-3,2 ) , С ( -2,-6,-3 ) , D ( -1,-8,7 ).
А ( -6,5,5 ) , В ( 4,-8,-4 ) , С ( -1,7,1 ) , D ( -2,0,-4 ).
Задание 2.3.
Даны
три вектора
![]() ,
,![]() ,
,![]() . Найти :
. Найти :
косинус угла между векторами
 и
и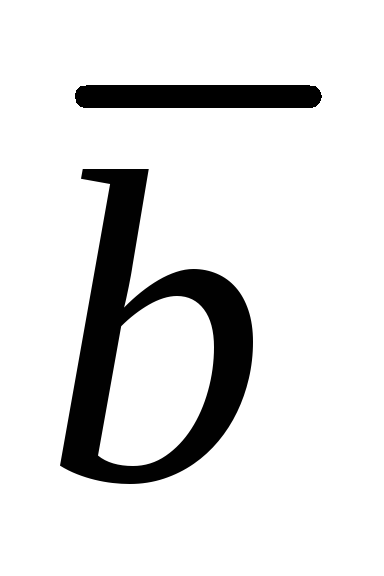 ;
;выяснить компланарны ли вектора
 ,
, ,
, ;
;если вектора
 ,
, ,
, компланарны, найти площадь параллелограмма,
построенного на векторах
компланарны, найти площадь параллелограмма,
построенного на векторах и
и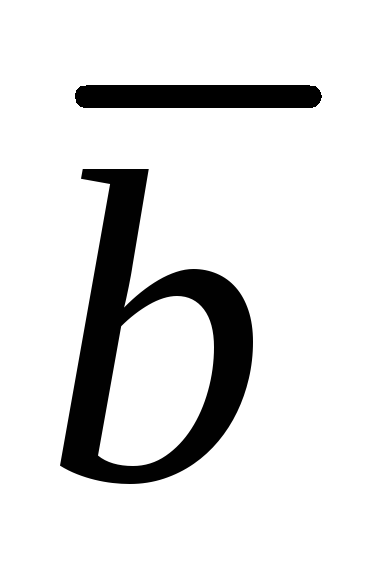 , как на сторонах, а если
, как на сторонах, а если ,
,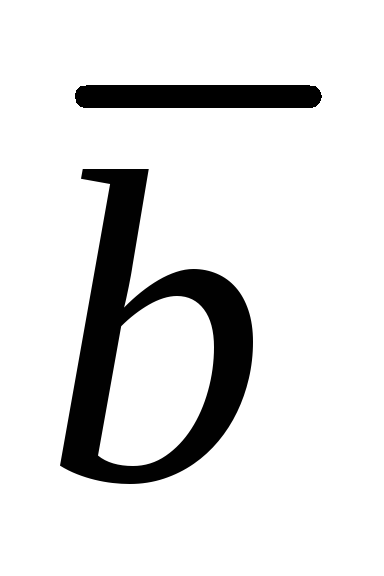 ,
, некомпланарны – найти объем
параллелепипеда, построенного на
векторах
некомпланарны – найти объем
параллелепипеда, построенного на
векторах ,
, ,
, , как на ребрах.
, как на ребрах.
 (
2,1,1 ) ,
(
2,1,1 ) ,
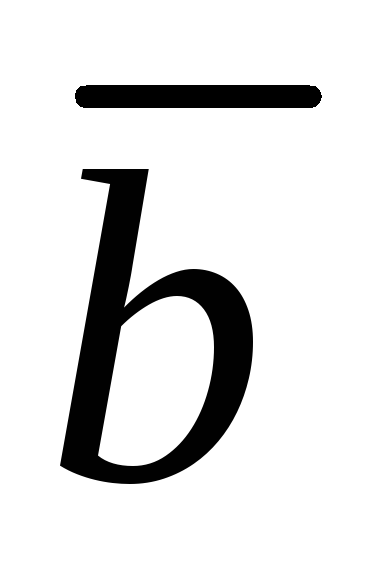 ( 19,11,17 ) ,
( 19,11,17 ) , ( 7,4,6 ) .
( 7,4,6 ) . (
-2,4,-1 ) ,
(
-2,4,-1 ) ,
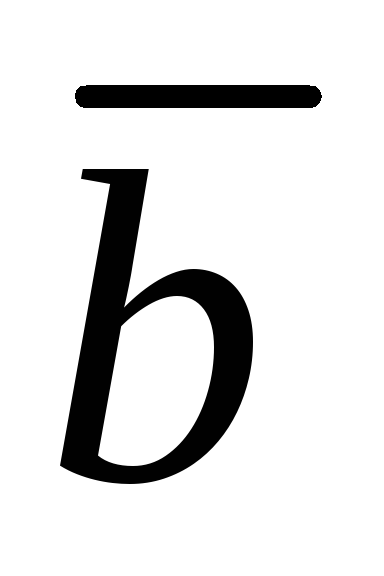 ( 0,-2,-1 ) ,
( 0,-2,-1 ) , ( -7,10,-5 ) .
( -7,10,-5 ) . (
-4,7,6 ) ,
(
-4,7,6 ) ,
 ( -3,3,3 ) ,
( -3,3,3 ) , ( 3,0,-1 ) .
( 3,0,-1 ) . (
1,-2,1 ) ,
(
1,-2,1 ) ,
 ( 3,3,1 ) ,
( 3,3,1 ) , ( 1,1,1 ) .
( 1,1,1 ) . (
6,2,6 ) ,
(
6,2,6 ) ,
 ( 4,1,1 ) ,
( 4,1,1 ) , ( -9,-4,-9 ) .
( -9,-4,-9 ) . (
-2,-1,0 ) ,
(
-2,-1,0 ) ,
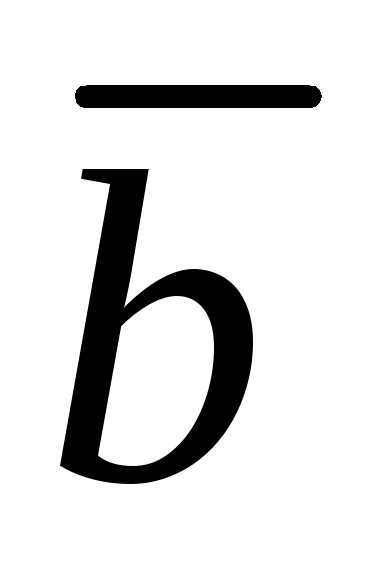 ( 3,1,-1 ) ,
( 3,1,-1 ) , ( 5,2,-1 ) .
( 5,2,-1 ) . (
4,3,1 ) ,
(
4,3,1 ) ,
 ( 2,2,2 ) ,
( 2,2,2 ) , ( 1,-2,1 ) .
( 1,-2,1 ) . (
6,7,4 ) ,
(
6,7,4 ) ,
 ( 4,3,1 ) ,
( 4,3,1 ) , ( 4,0,-2 ) .
( 4,0,-2 ) . (
1,2,3 ) ,
(
1,2,3 ) ,
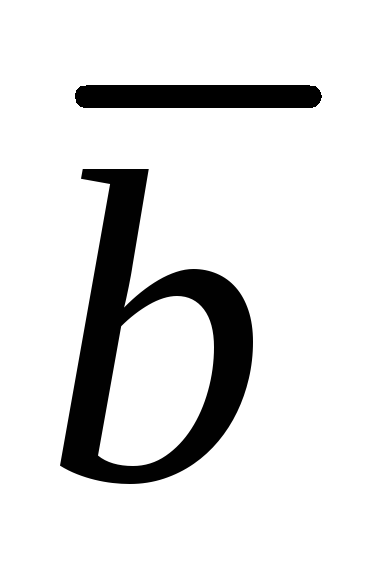 ( 3,2,1 ) ,
( 3,2,1 ) , ( 1,-3,-7 ) .
( 1,-3,-7 ) . (
2,3,4 ) ,
(
2,3,4 ) ,
 ( 1,-1,-3 ) ,
( 1,-1,-3 ) , ( 3,2,1 ) .
( 3,2,1 ) . (
1,5,2 ) ,
(
1,5,2 ) ,
 ( -1,1,-1 ) ,
( -1,1,-1 ) , ( 1,1,1 ) .
( 1,1,1 ) . (
2,3,4 ) ,
(
2,3,4 ) ,
 ( 3,1,-1 ) ,
( 3,1,-1 ) , ( 3,2,1 ) .
( 3,2,1 ) . (
2,3,1 ) ,
(
2,3,1 ) ,
 ( 2,2,2 ) ,
( 2,2,2 ) , ( -1,0,-1 ) .
( -1,0,-1 ) . (
3,1,3 ) ,
(
3,1,3 ) ,
 ( 4,1,1 ) ,
( 4,1,1 ) , ( -9,-4,-9 ) .
( -9,-4,-9 ) . (
4,3,6 ) ,
(
4,3,6 ) ,
 ( -1,-2,-1 ) ,
( -1,-2,-1 ) , ( 2,1,2 ) .
( 2,1,2 ) . (
4,-1,1 ) ,
(
4,-1,1 ) ,
 ( 3,0,1 ) ,
( 3,0,1 ) , ( 8,-3,1 ) .
( 8,-3,1 ) . (
-1,1,1 ) ,
(
-1,1,1 ) ,
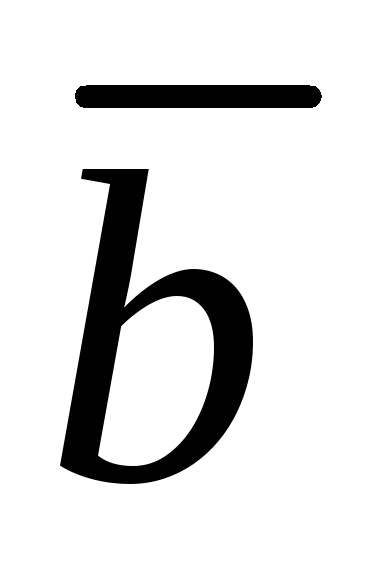 ( 6,1,8 ) ,
( 6,1,8 ) , ( 3,0,3 ) .
( 3,0,3 ) . (
0,1,3 ) ,
(
0,1,3 ) ,
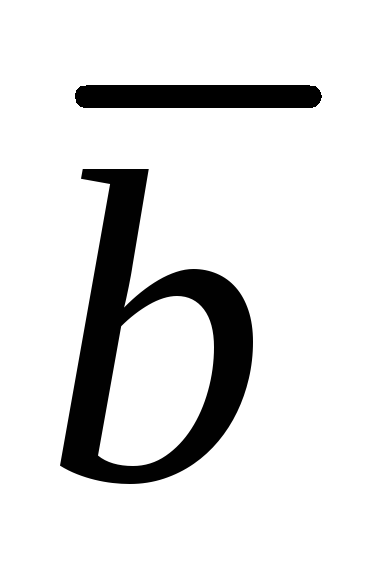 ( -5,-4,-5 ) ,
( -5,-4,-5 ) , ( 2,1,2 ) .
( 2,1,2 ) . (
-6,-1,4 ) ,
(
-6,-1,4 ) ,
 ( -7,-3,1 ) ,
( -7,-3,1 ) , ( -4,-1,2 ) .
( -4,-1,2 ) . (
2,4,3 ) ,
(
2,4,3 ) ,
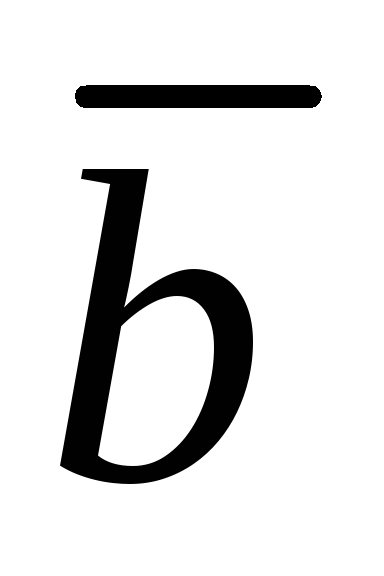 ( 0,1,1 ) ,
( 0,1,1 ) , ( 6,11,8 ) .
( 6,11,8 ) . (
4,3,5 ) ,
(
4,3,5 ) ,
 ( 3,3,4 ) ,
( 3,3,4 ) , ( 8,5,9 ) .
( 8,5,9 ) . (
4,1,2 ) ,
(
4,1,2 ) ,
 ( 1,1,-1 ) ,
( 1,1,-1 ) , ( 9,2,5 ) .
( 9,2,5 ) . (
2,1,1 ) ,
(
2,1,1 ) ,
 ( -1,-1,-1 ) ,
( -1,-1,-1 ) , ( 2,1,2 ) .
( 2,1,2 ) . (
1,0,-1 ) ,
(
1,0,-1 ) ,
 ( 8,3,-2 ) ,
( 8,3,-2 ) , ( 3,1,-1 ) .
( 3,1,-1 ) . (
4,3,1 ) ,
(
4,3,1 ) ,
 ( -2,-4,-3 ) ,
( -2,-4,-3 ) , ( 6,7,4 ) .
( 6,7,4 ) . (
2,4,3 ) ,
(
2,4,3 ) ,
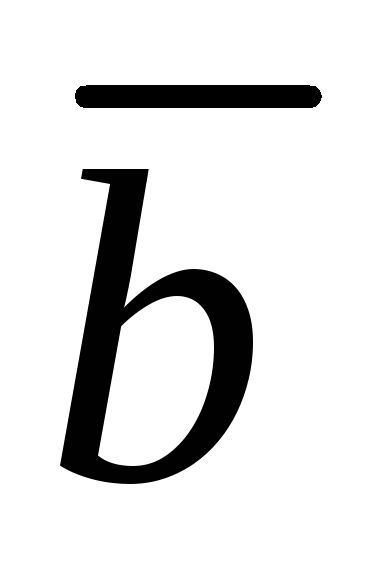 ( -2,-2,-3 ) ,
( -2,-2,-3 ) , ( 3,10,5 ) .
( 3,10,5 ) . (
4,2,4 ) ,
(
4,2,4 ) ,
 ( -2,0,-2 ) ,
( -2,0,-2 ) , ( 5,3,4 ) .
( 5,3,4 ) . (
4,7,5 ) ,
(
4,7,5 ) ,
 ( 2,3,2 ) ,
( 2,3,2 ) , ( 2,0,-1 ) .
( 2,0,-1 ) . (
7,3,4 ) ,
(
7,3,4 ) ,
 ( -1,-2,-1 ) ,
( -1,-2,-1 ) , ( 4,2,4 ) .
( 4,2,4 ) . (
2,1,2 ) ,
(
2,1,2 ) ,
 ( 6,3,4 ) ,
( 6,3,4 ) , ( -1,-2,-1 ) .
( -1,-2,-1 ) .
