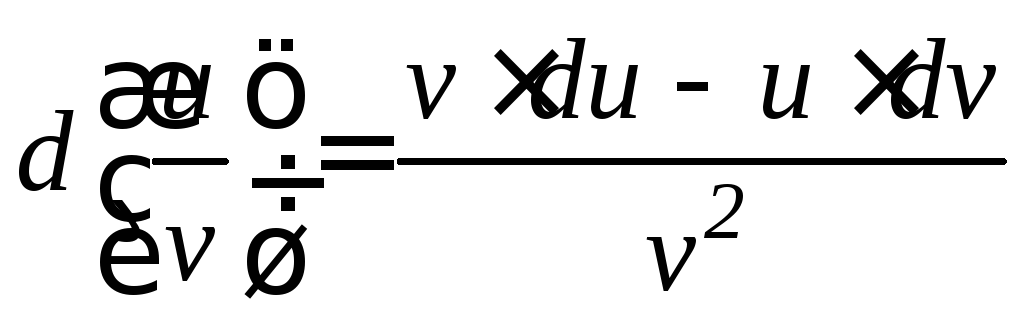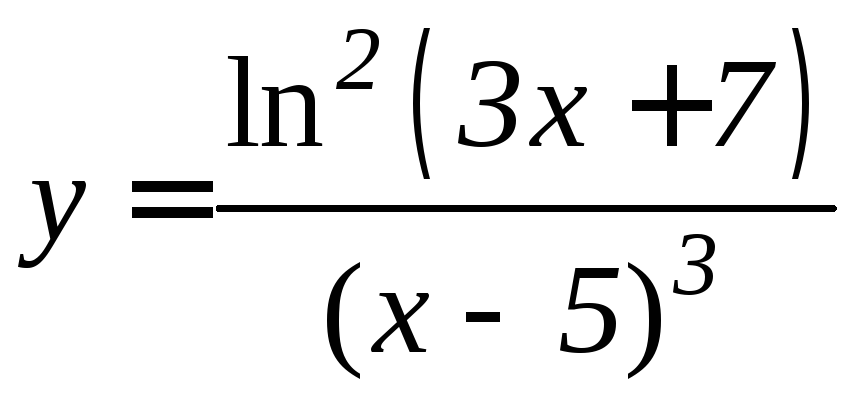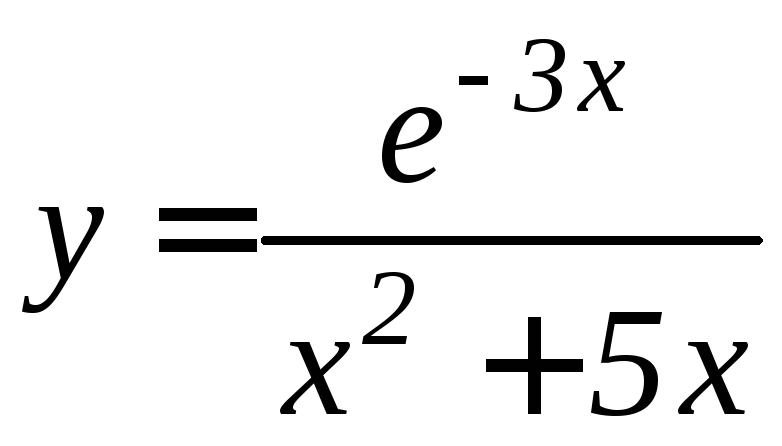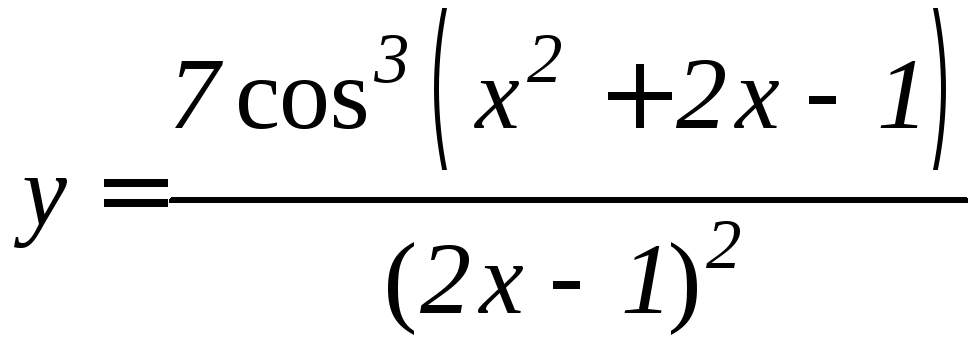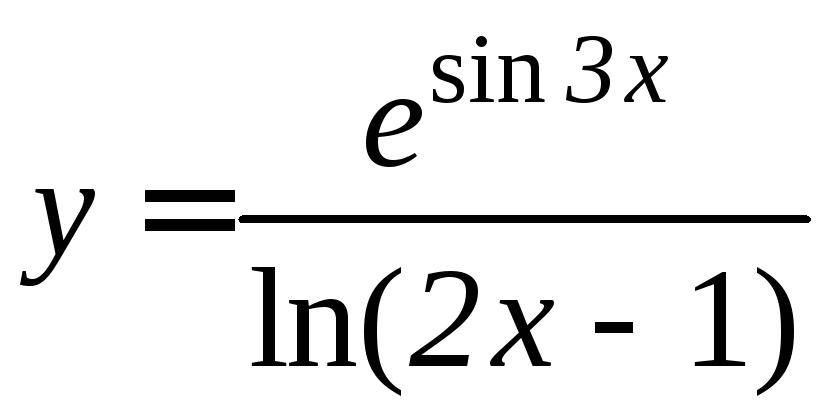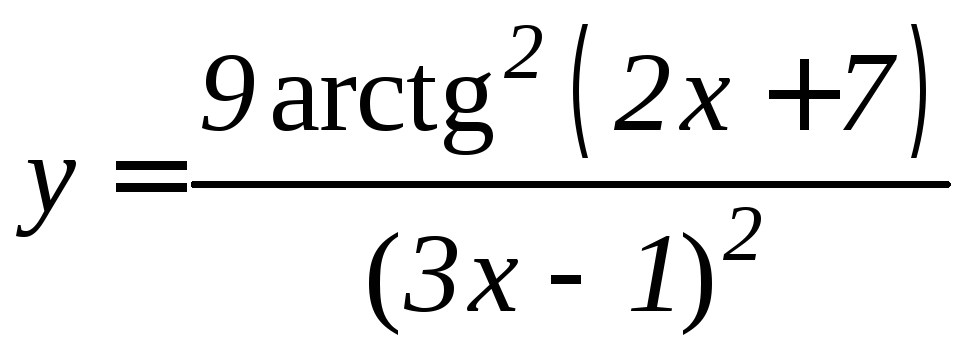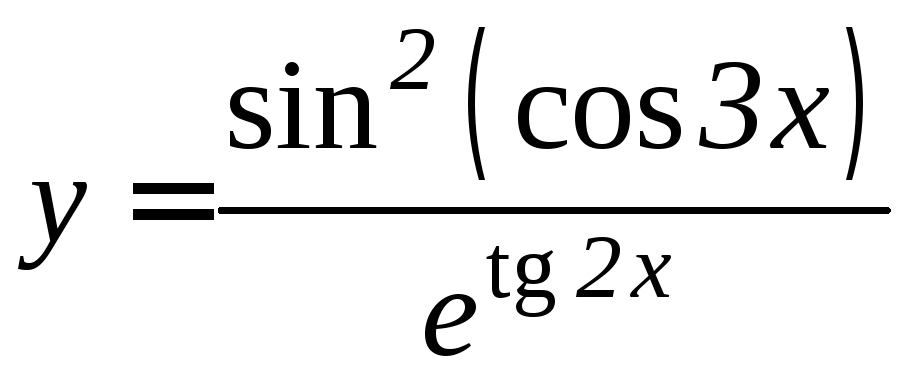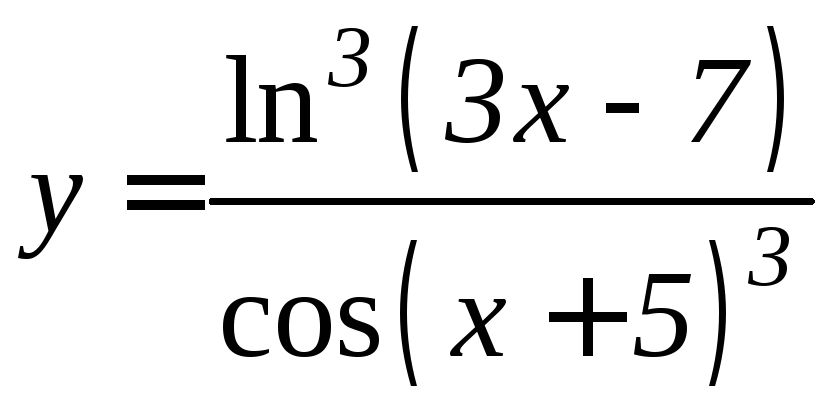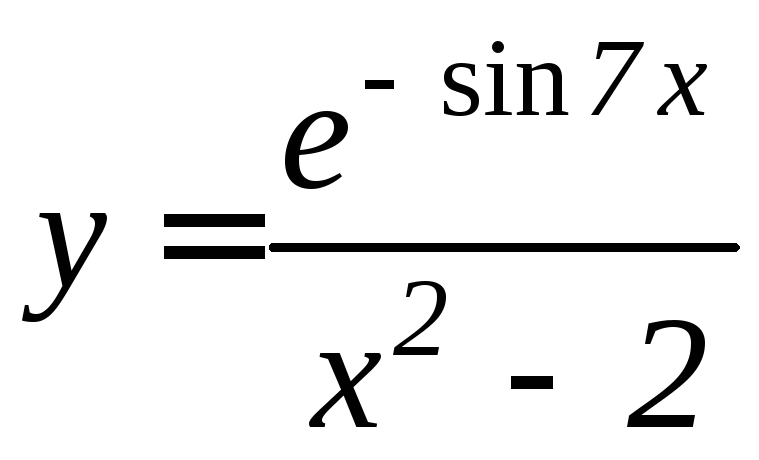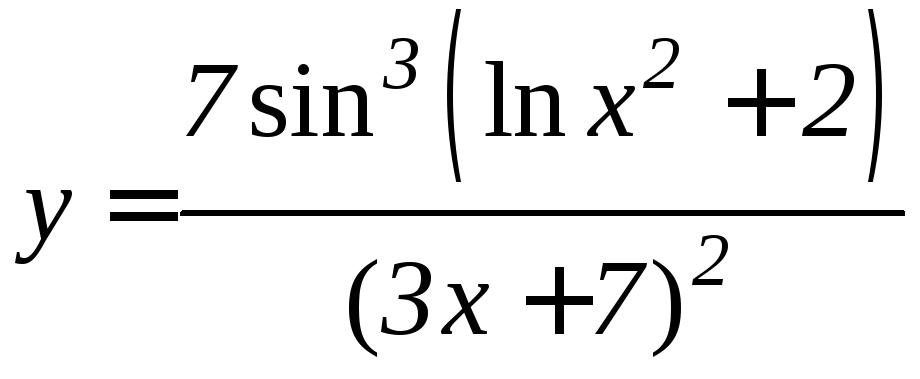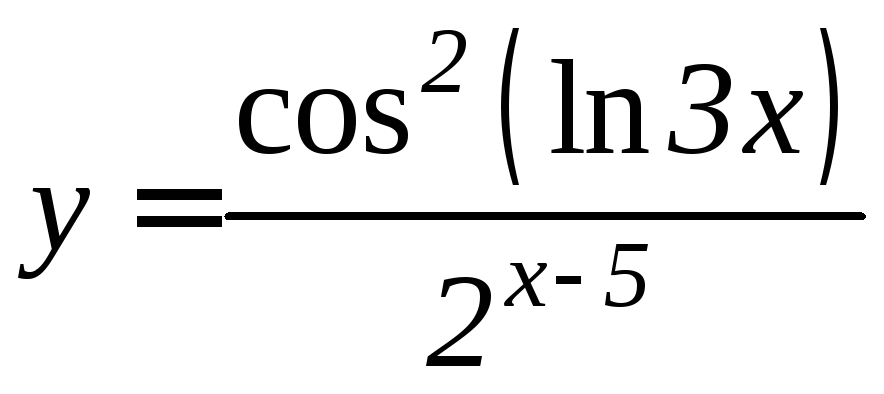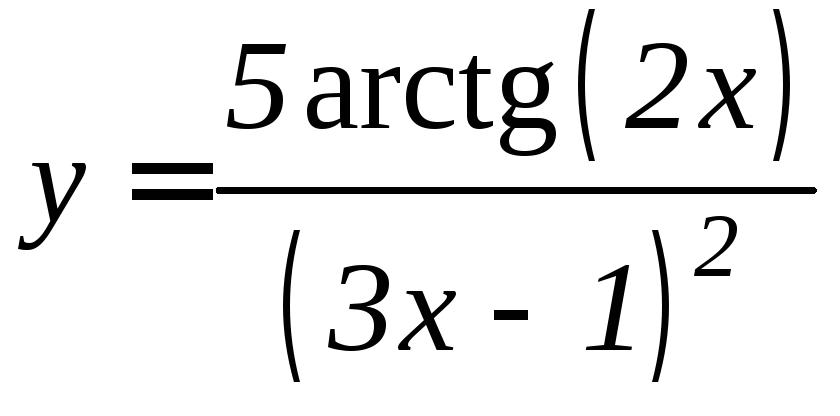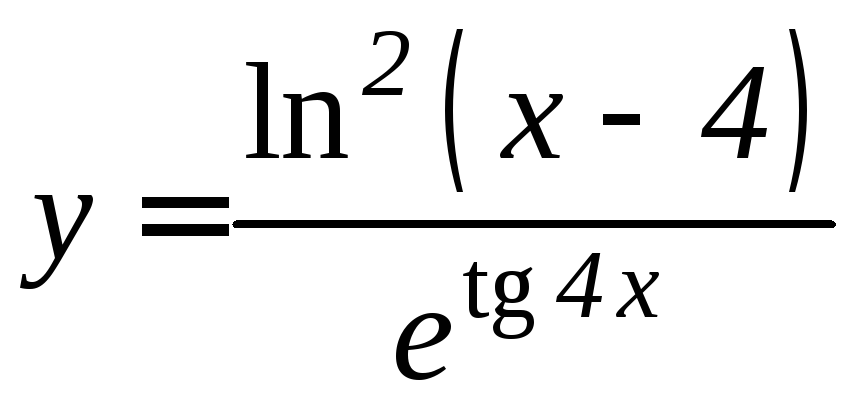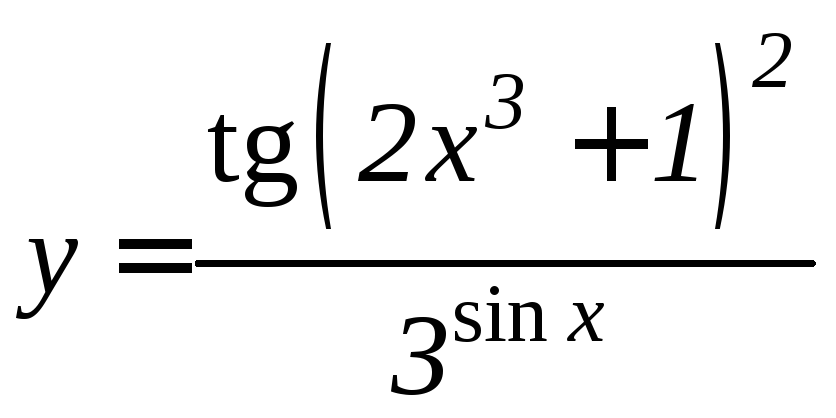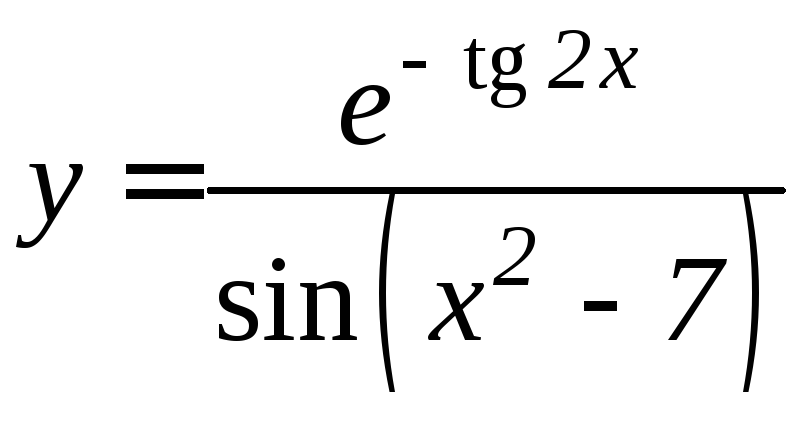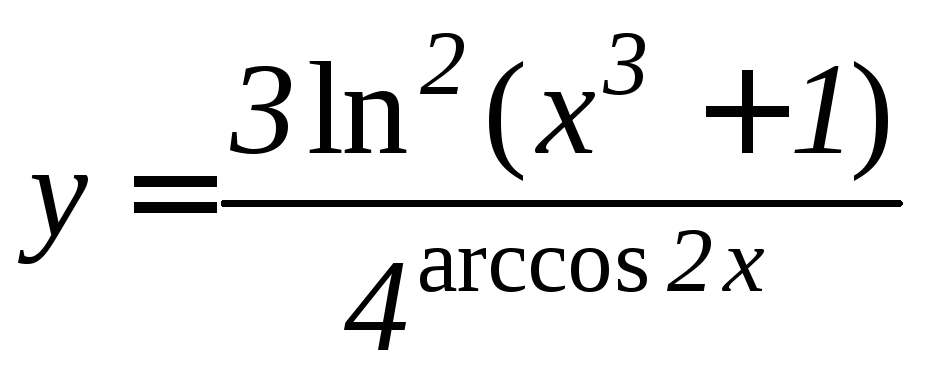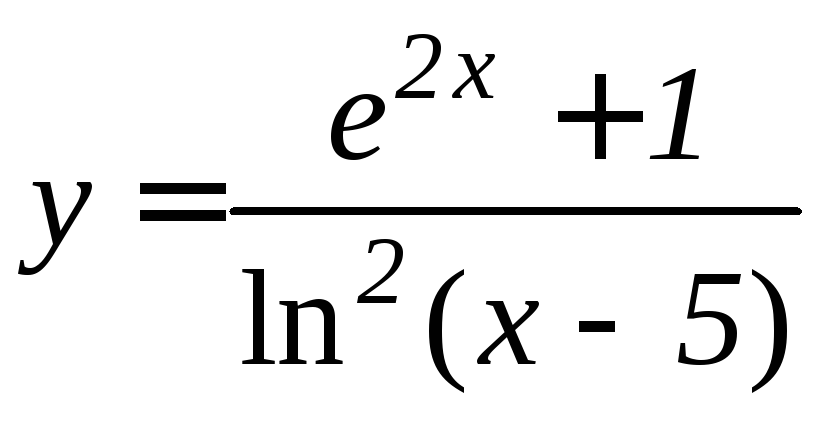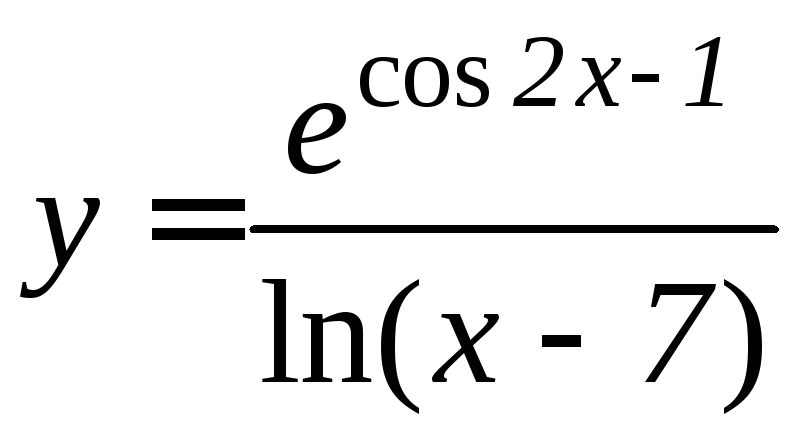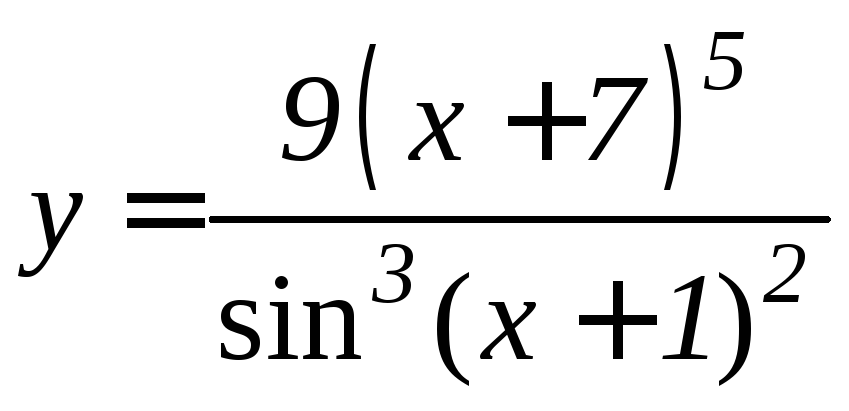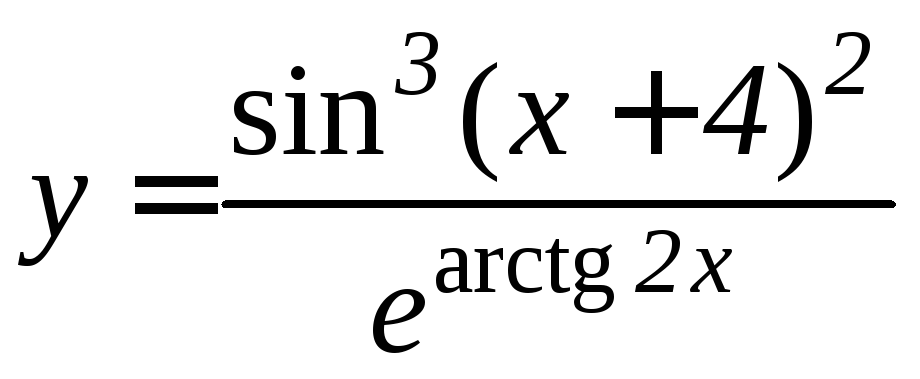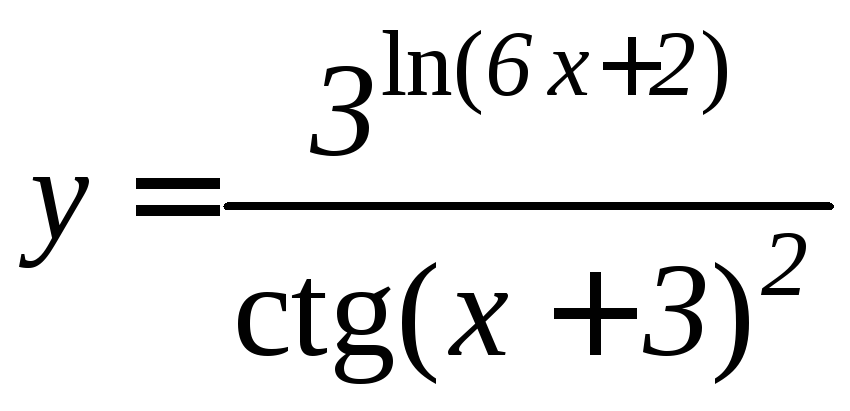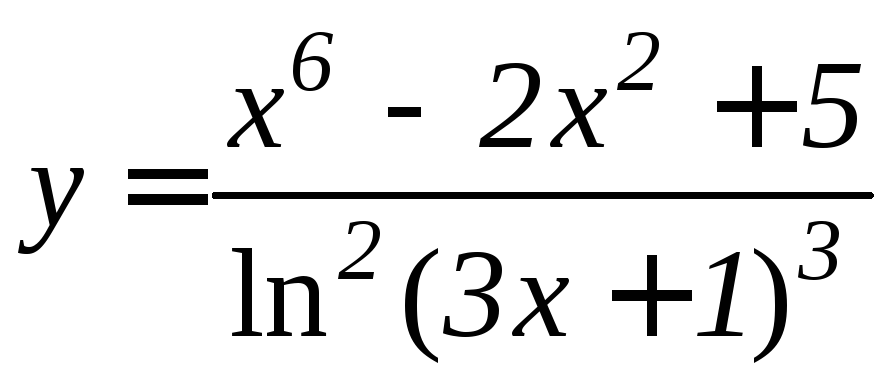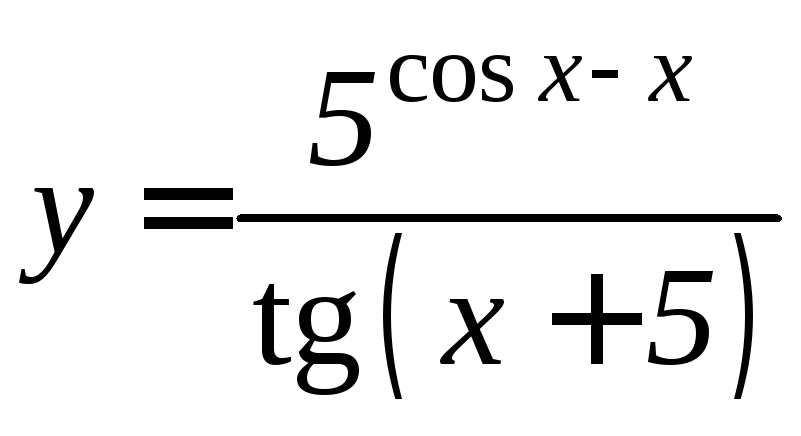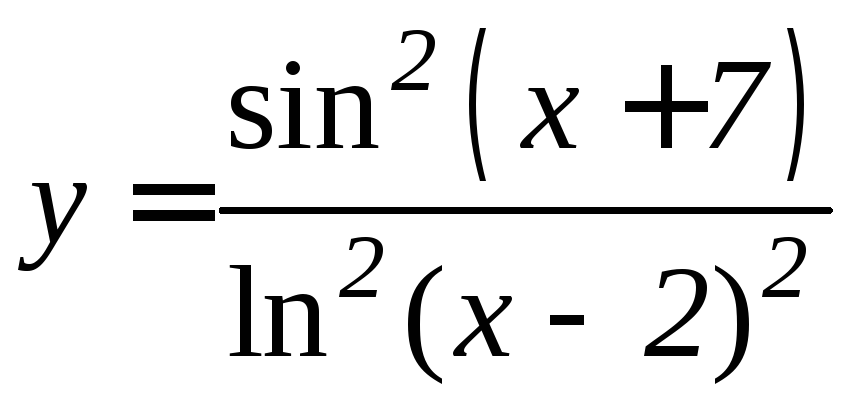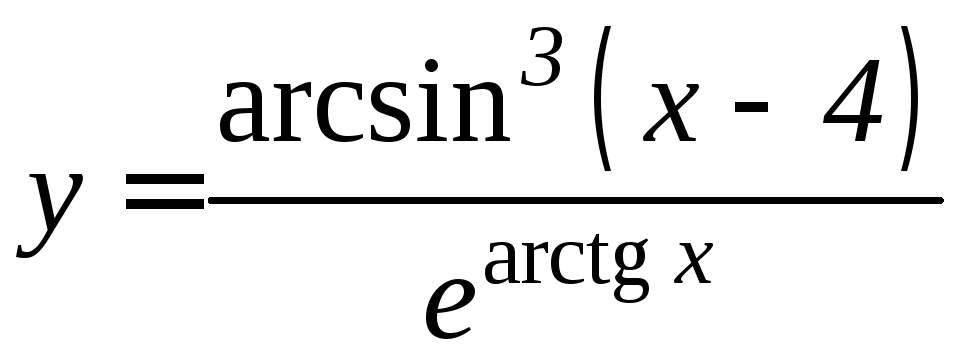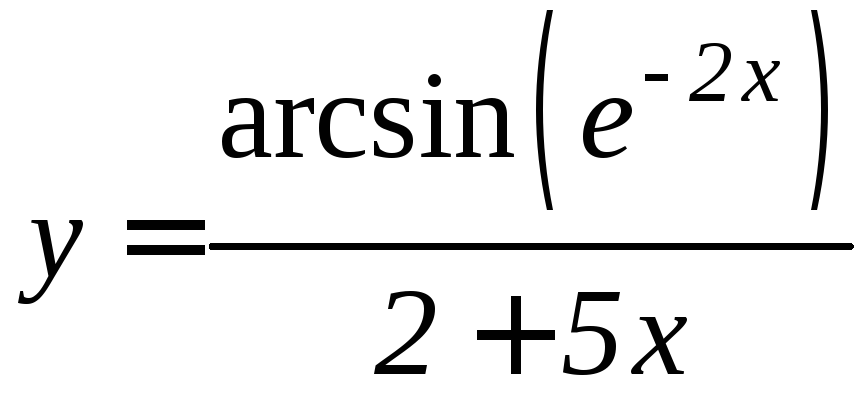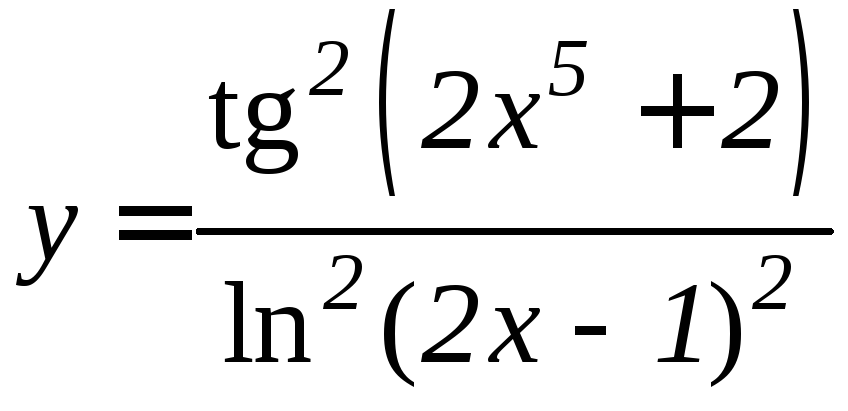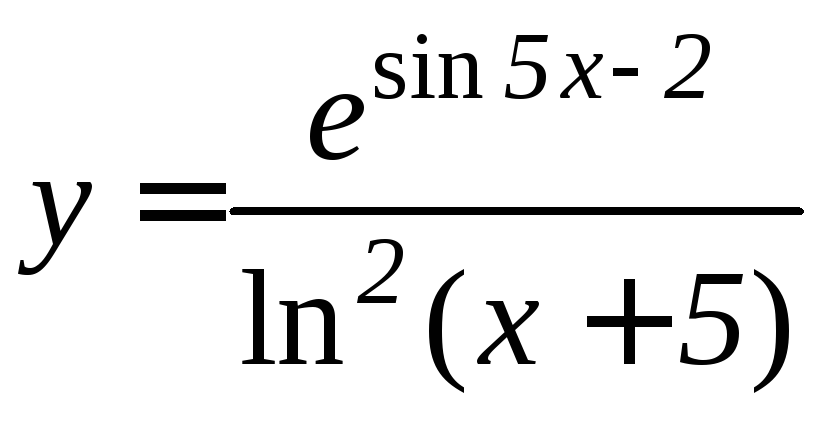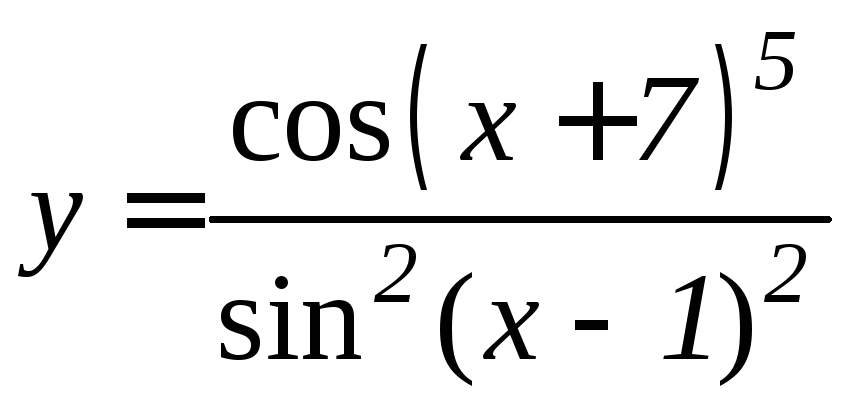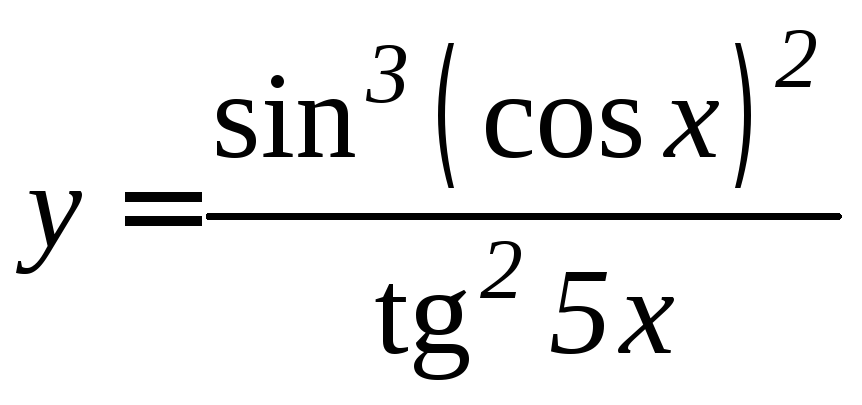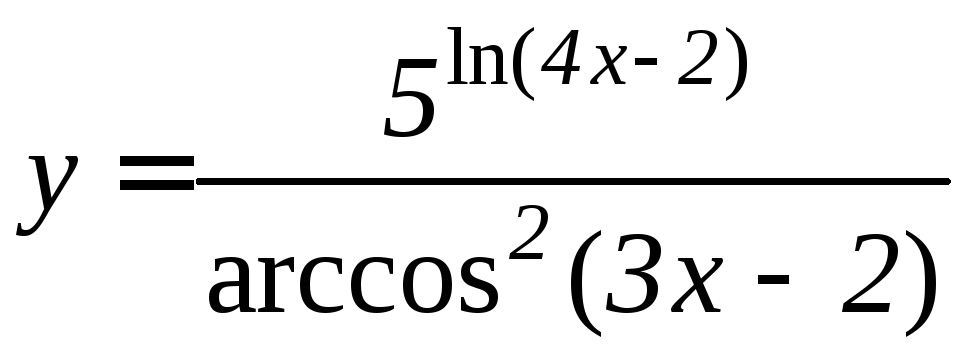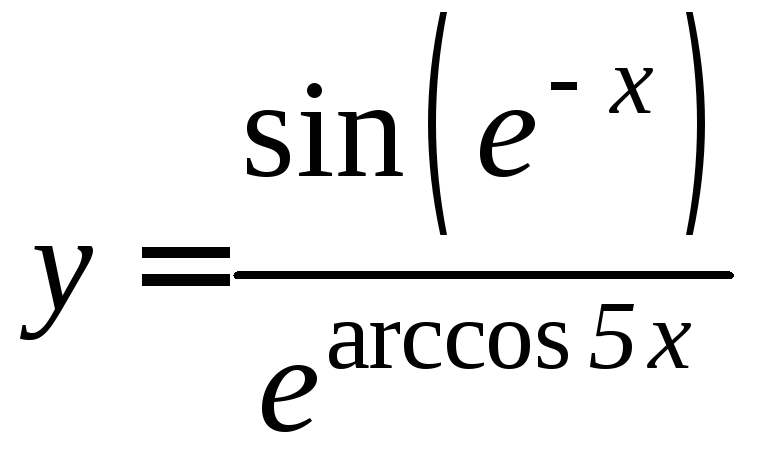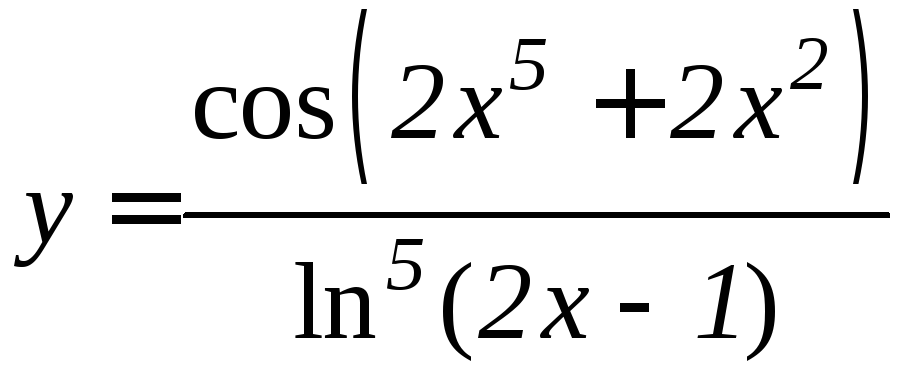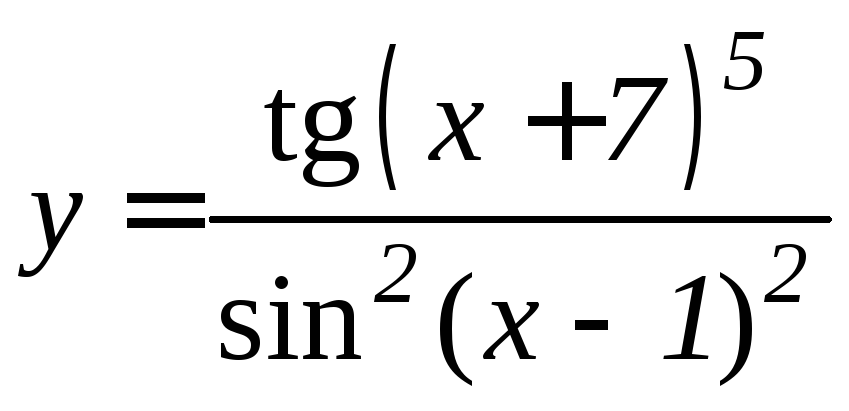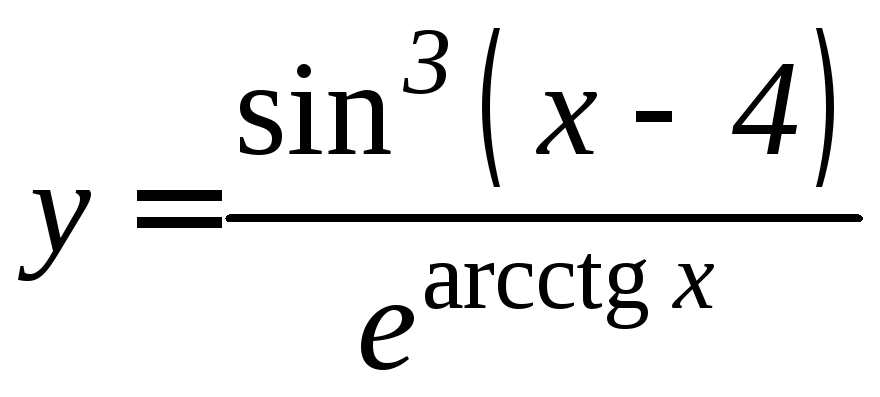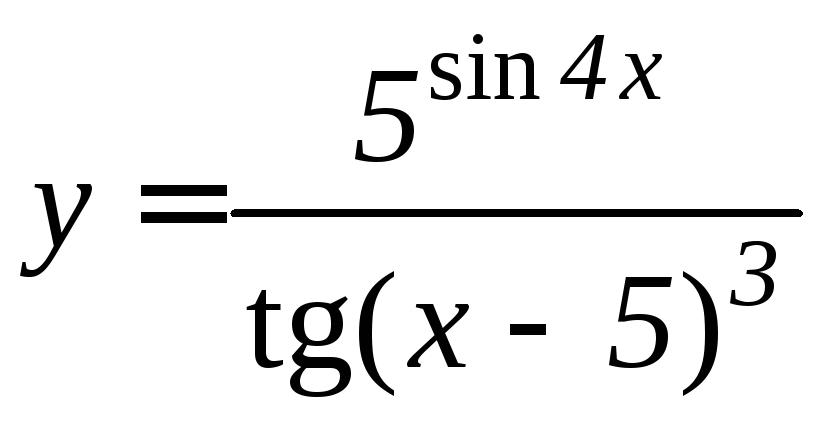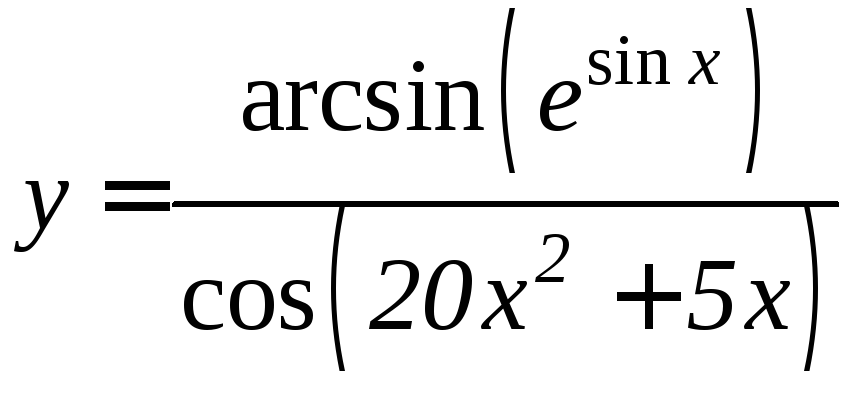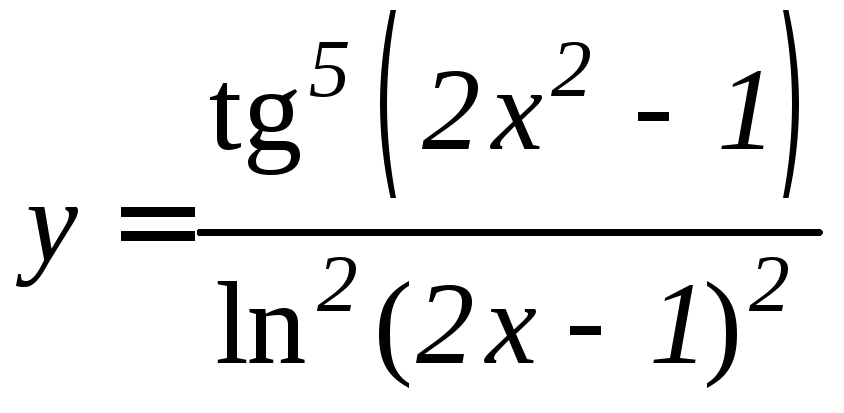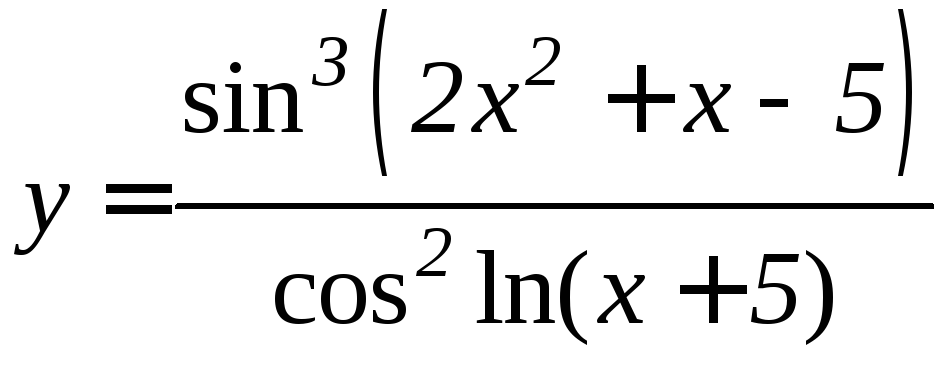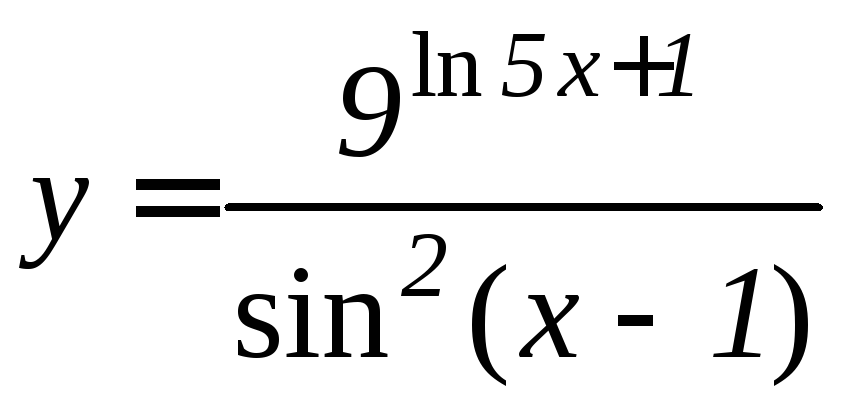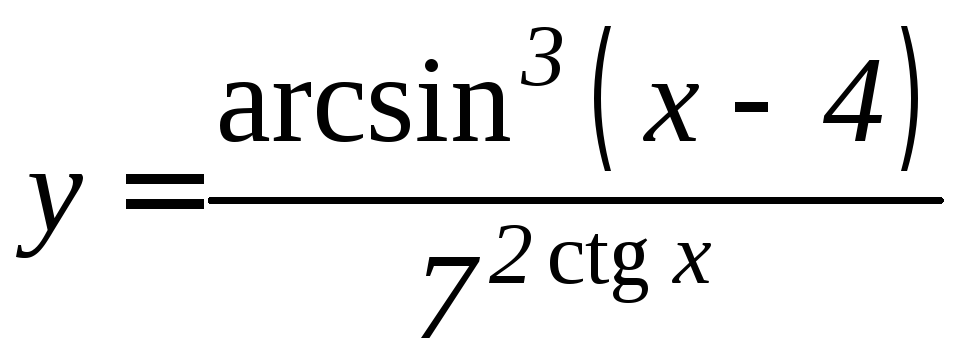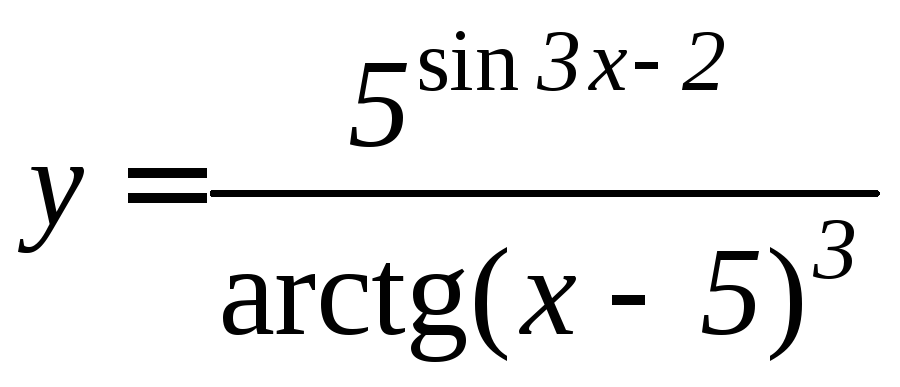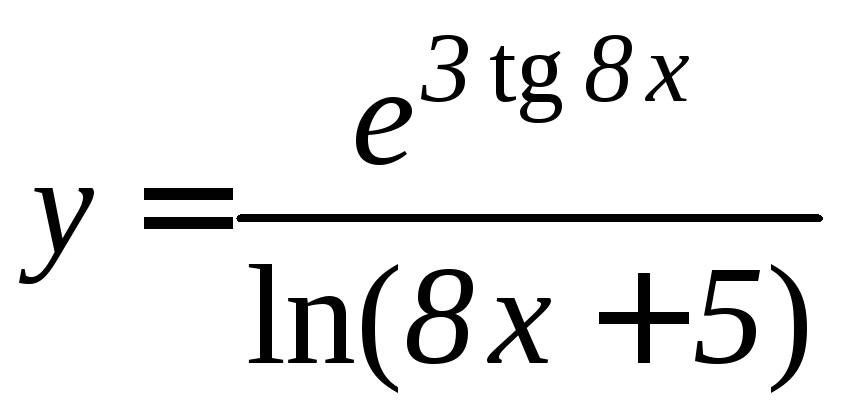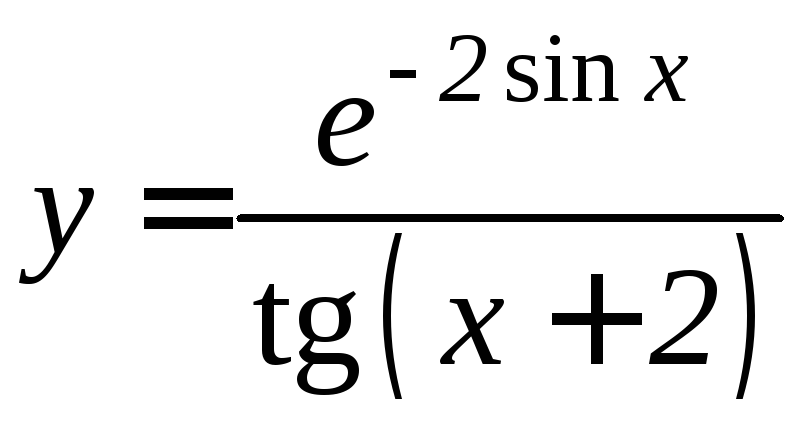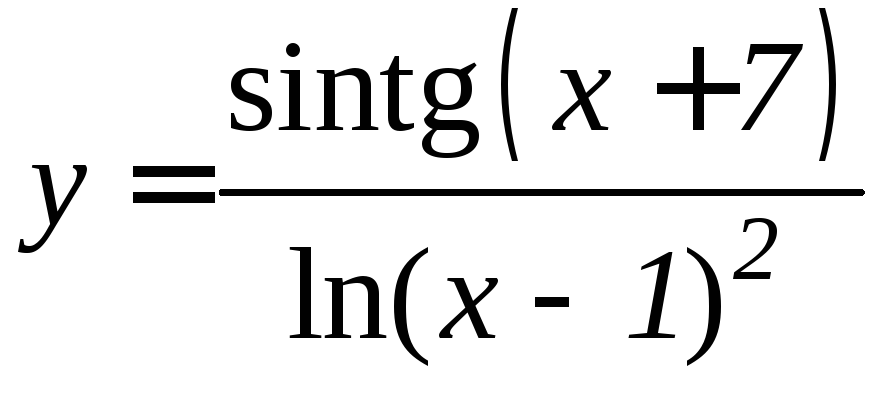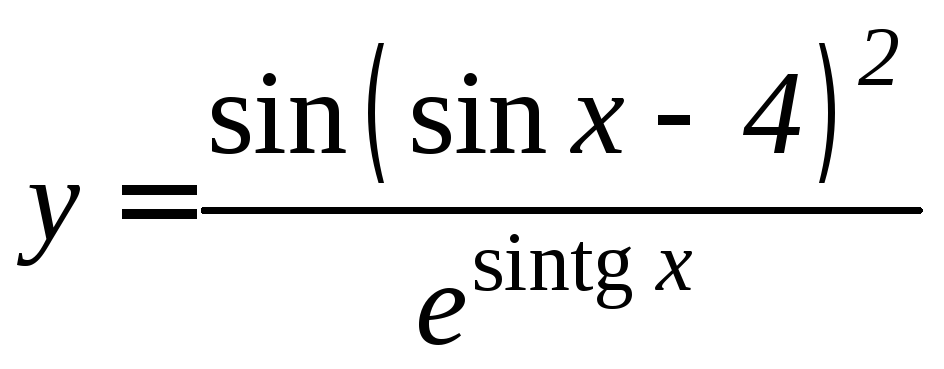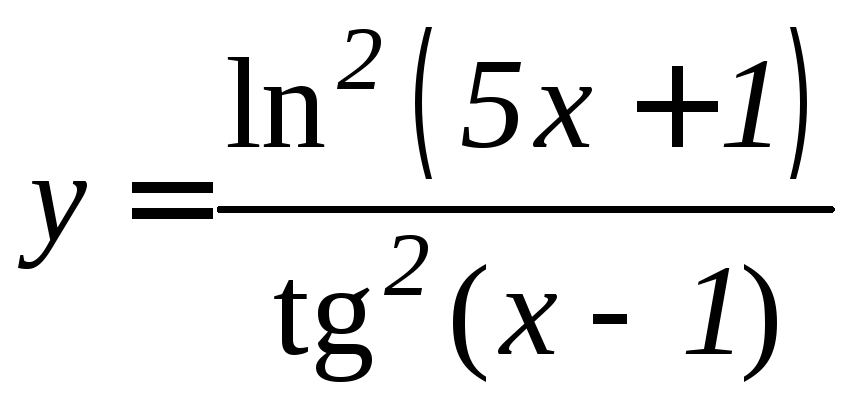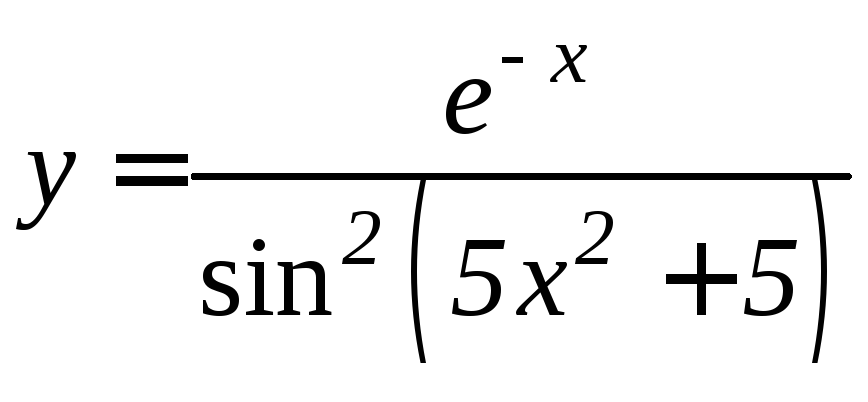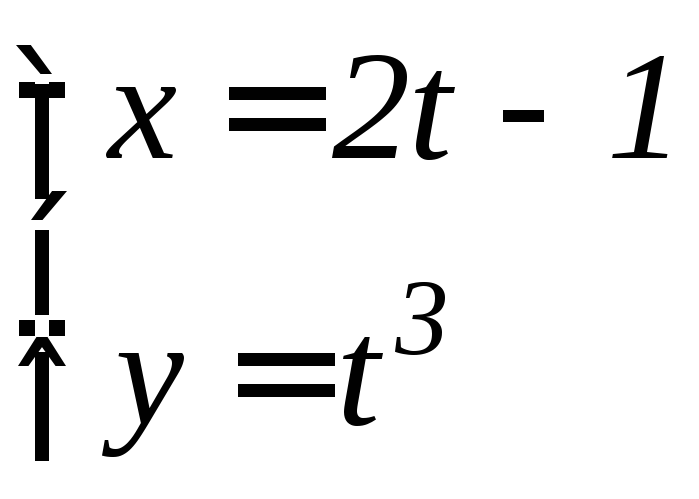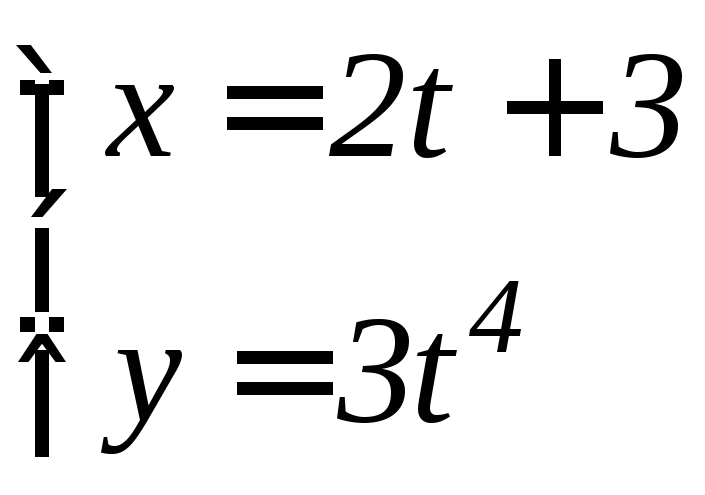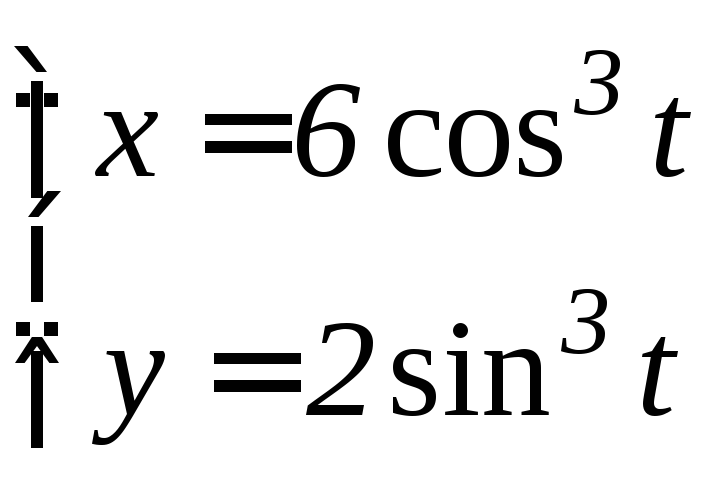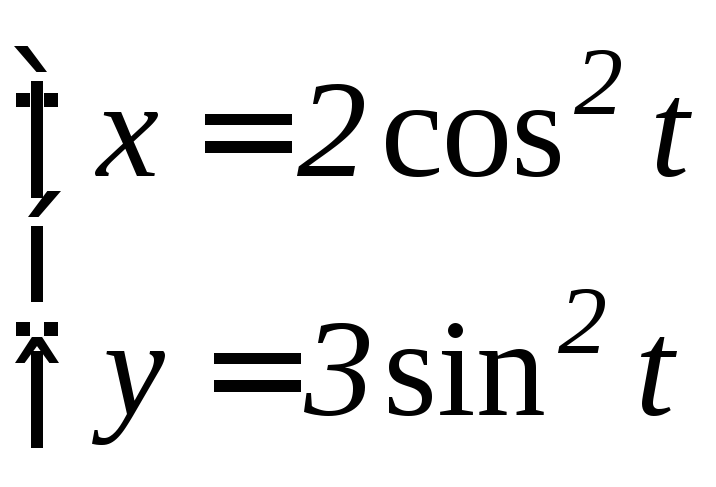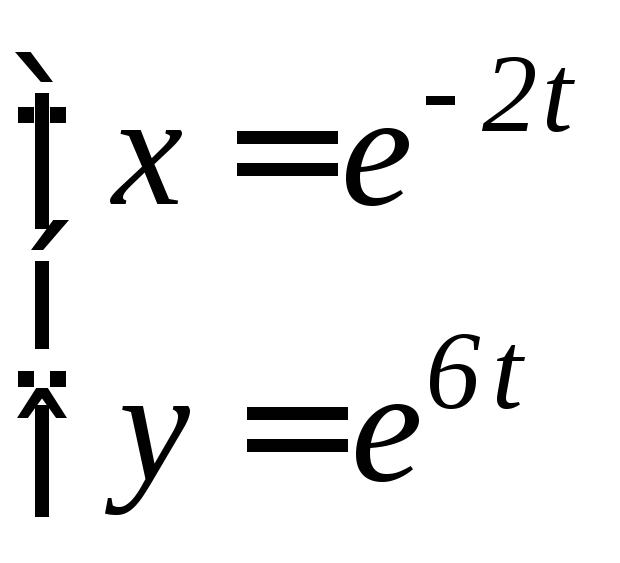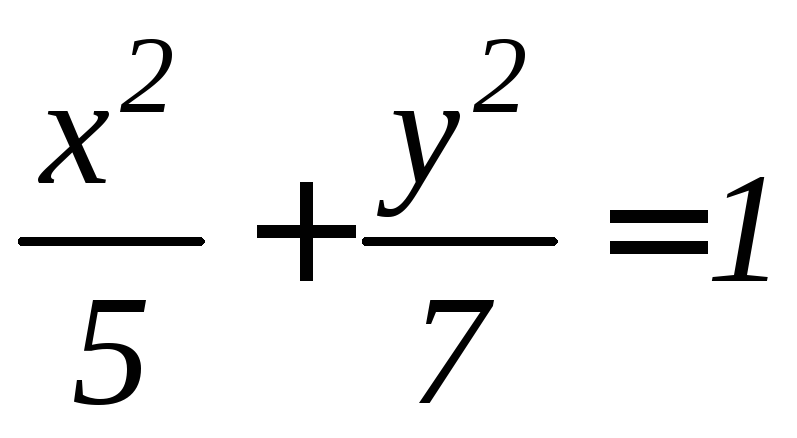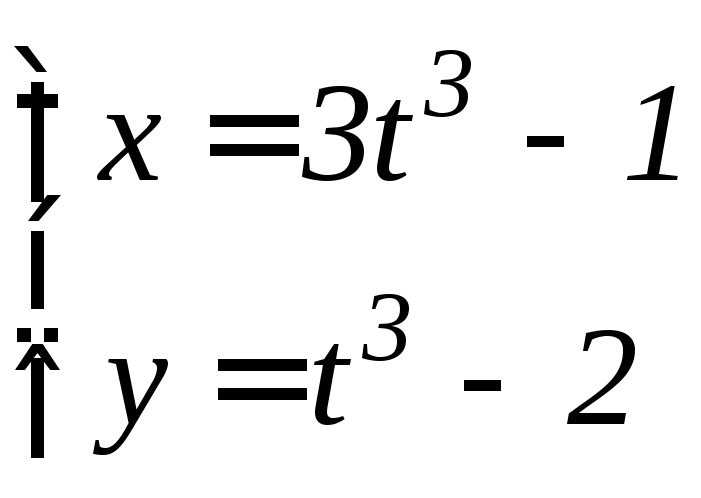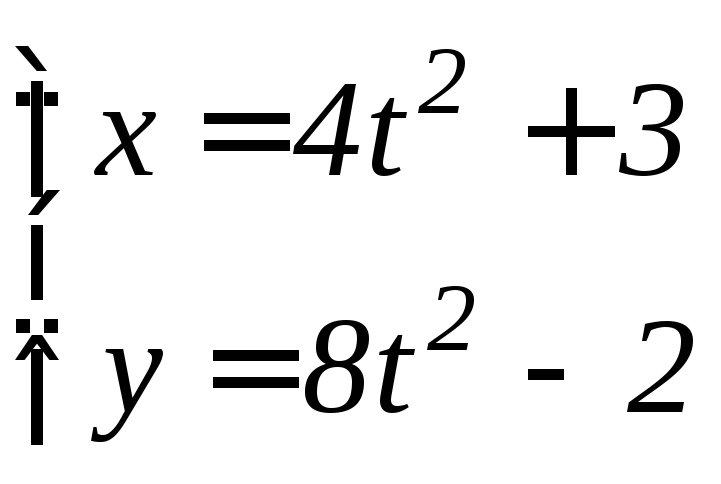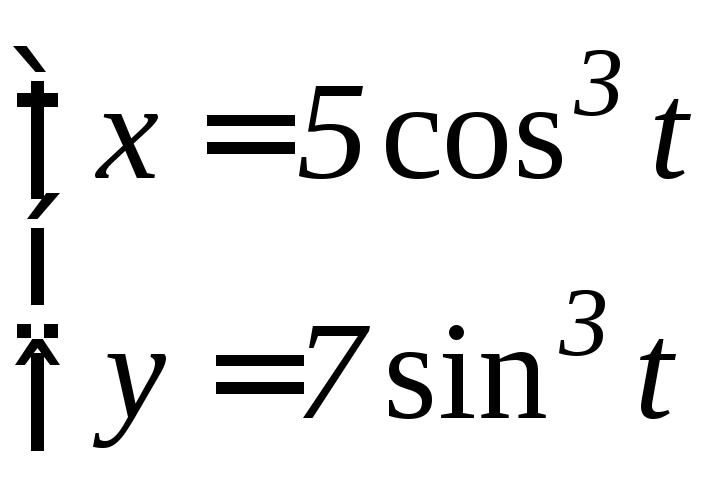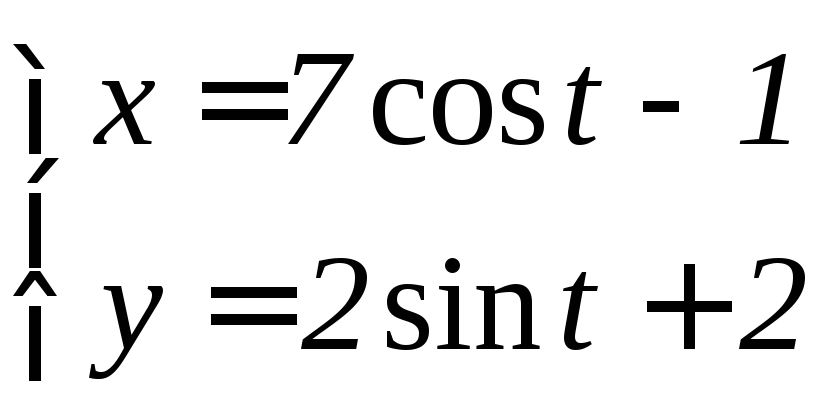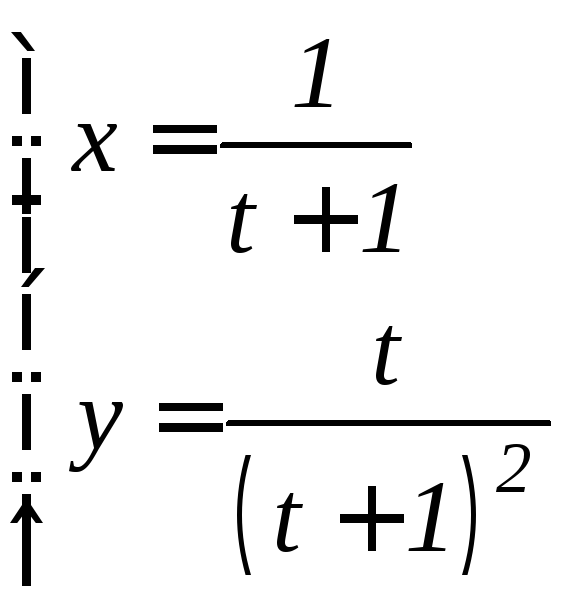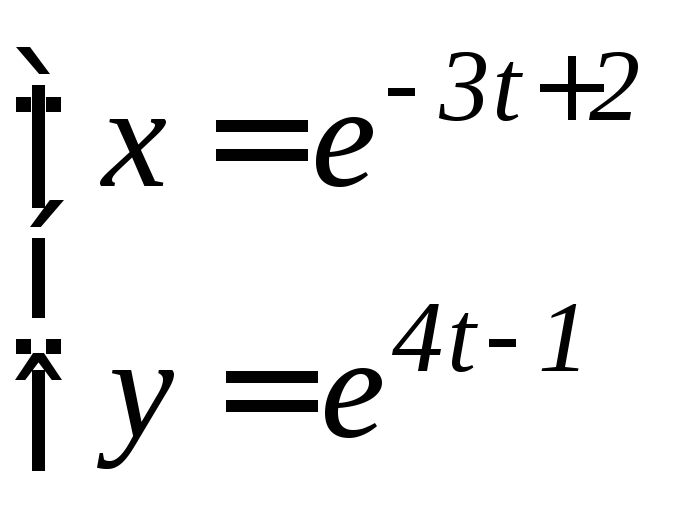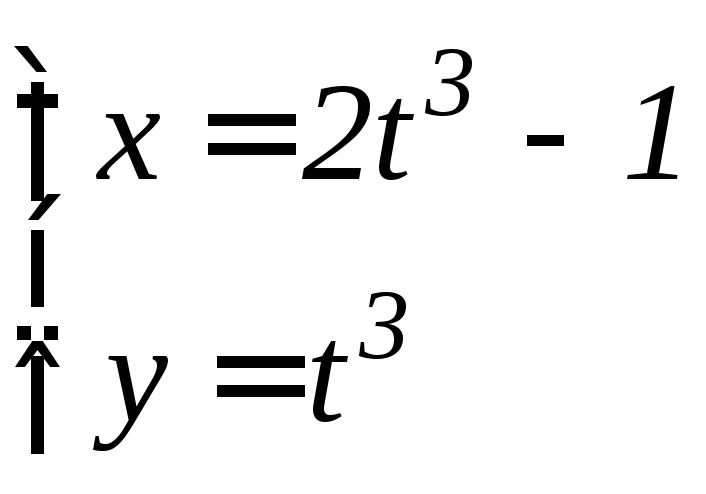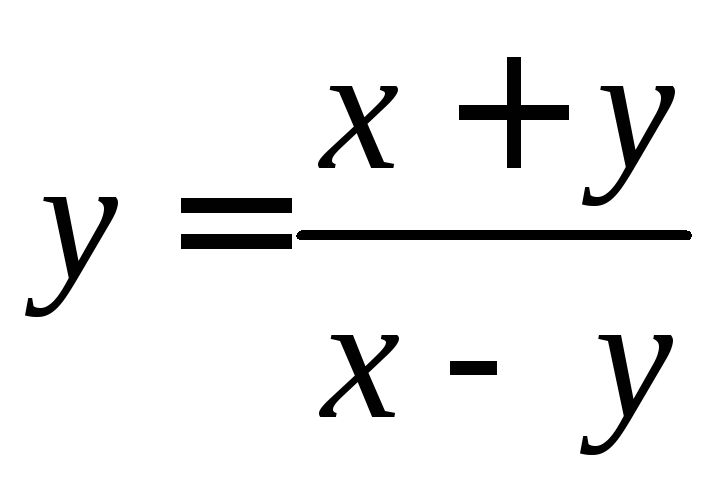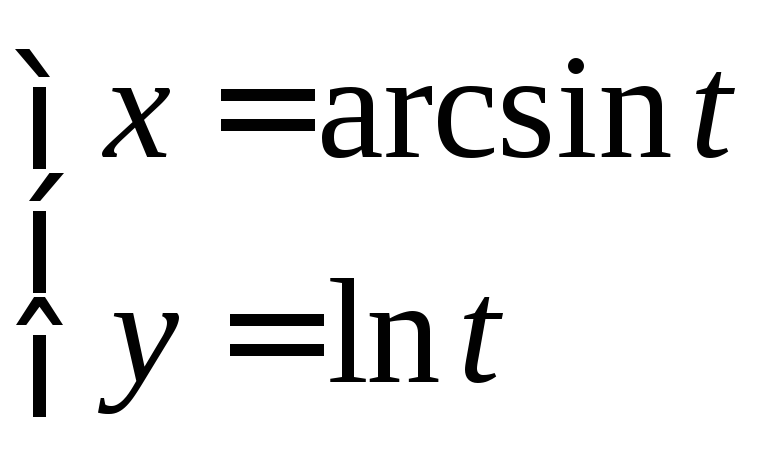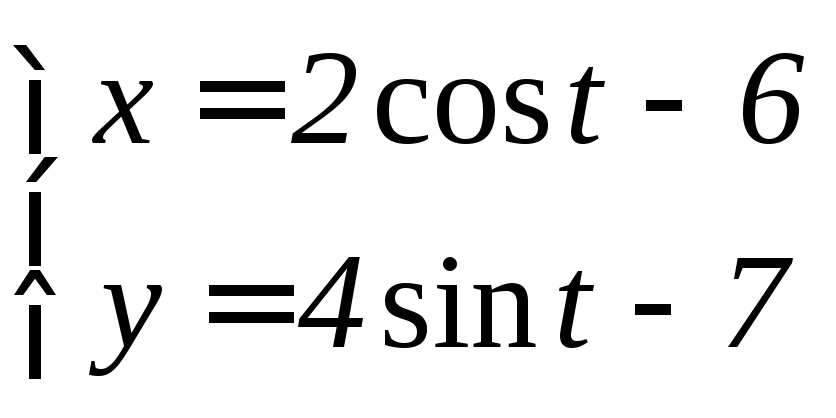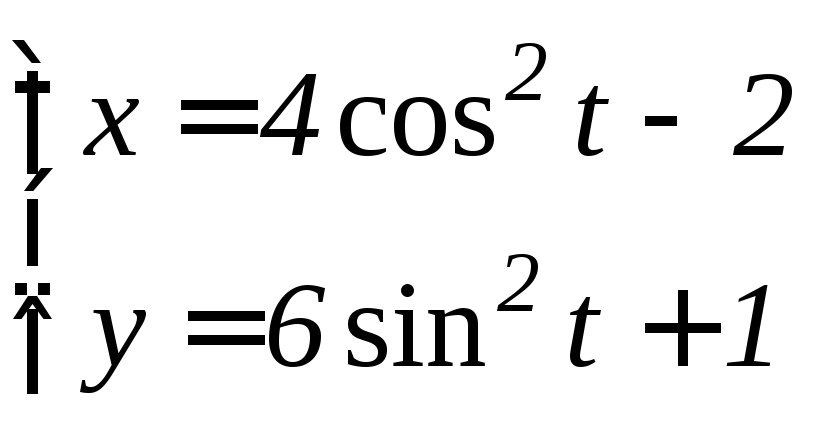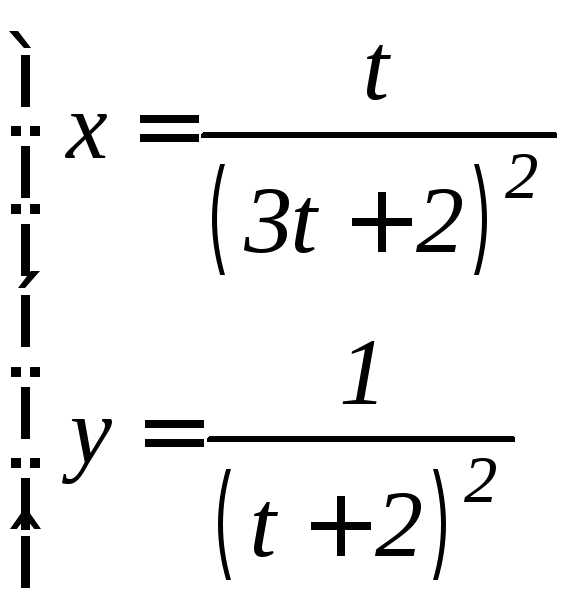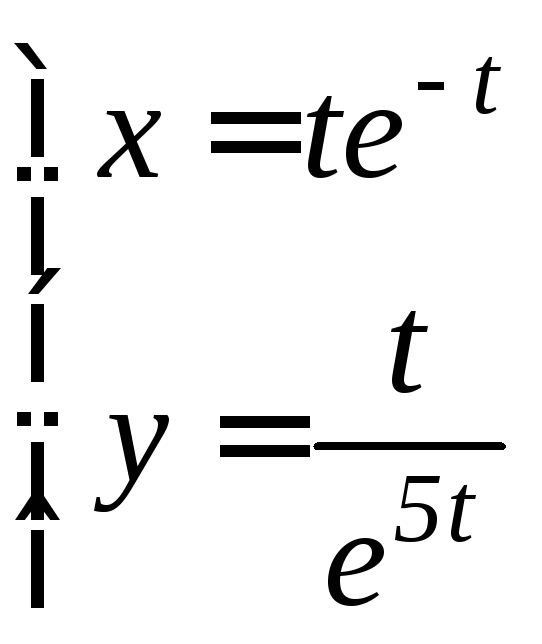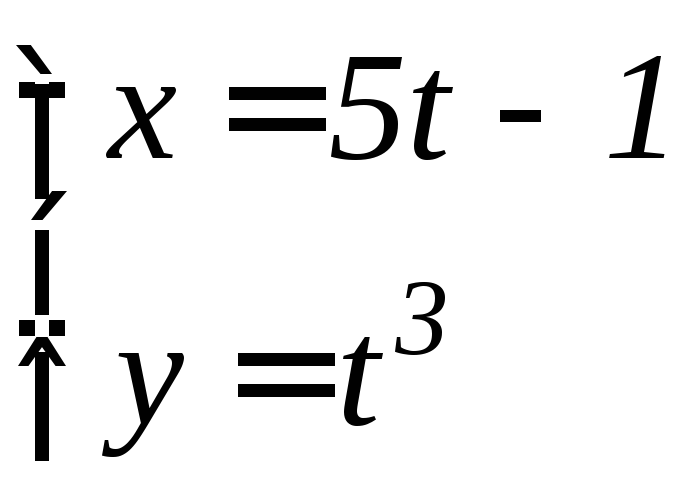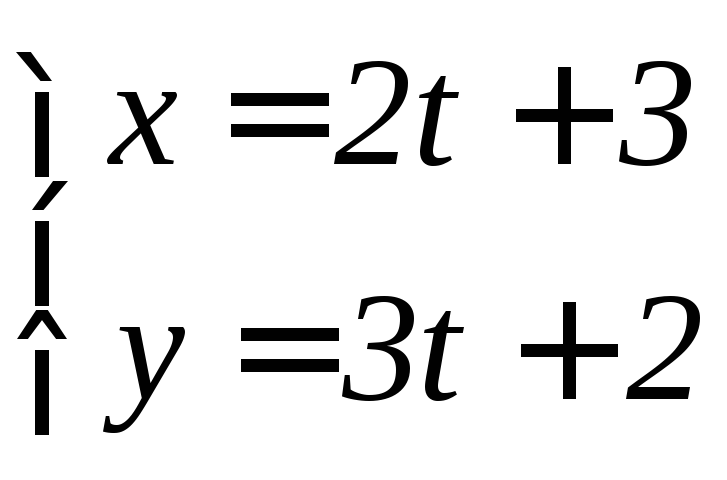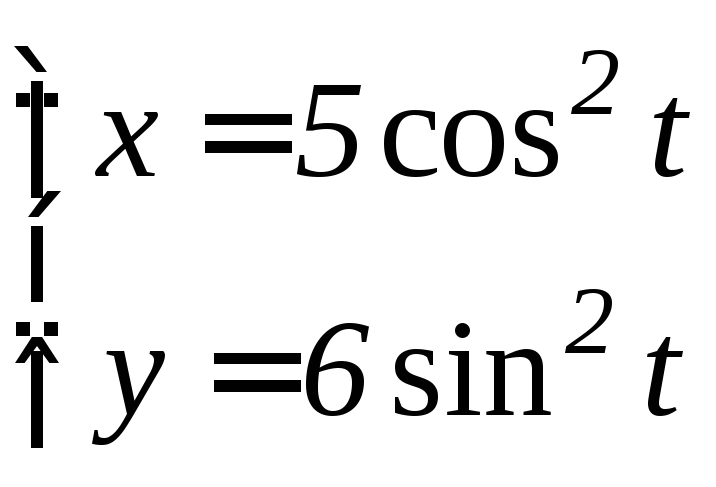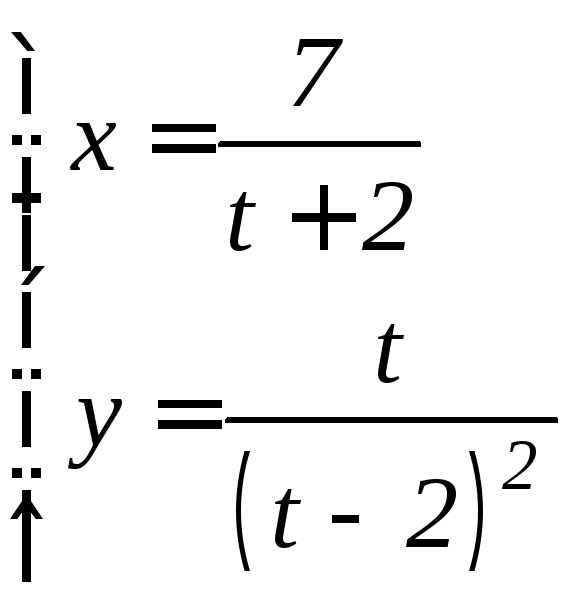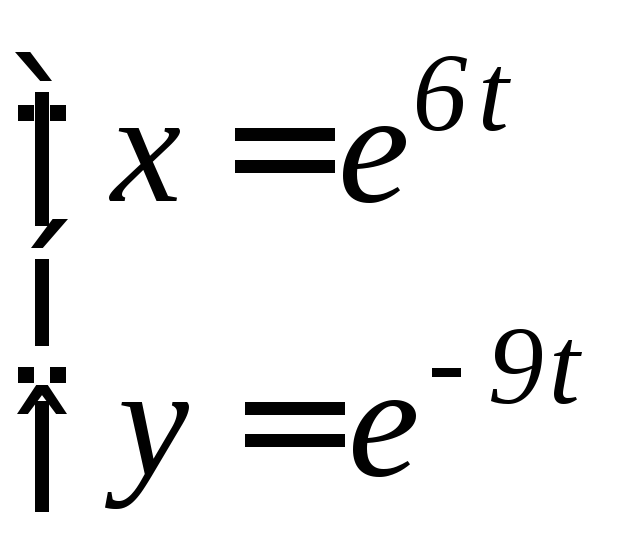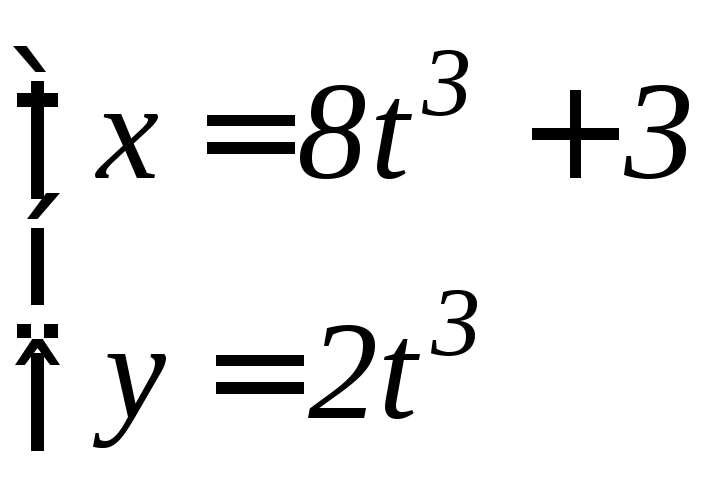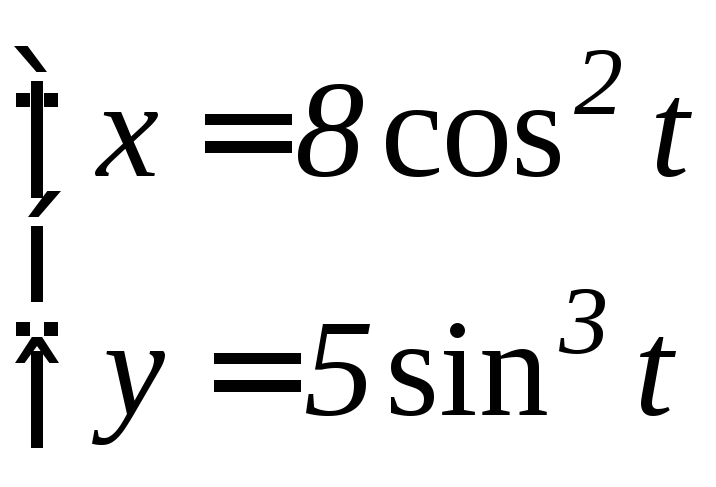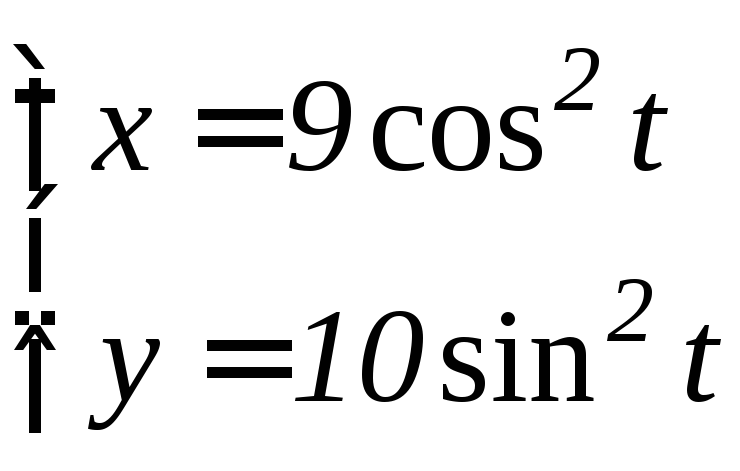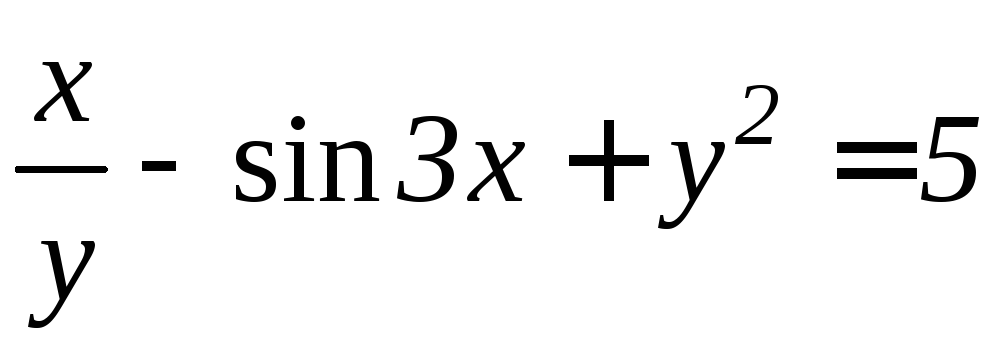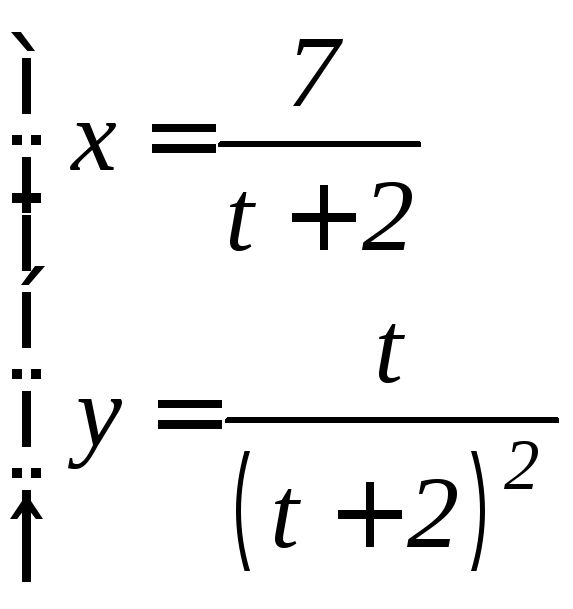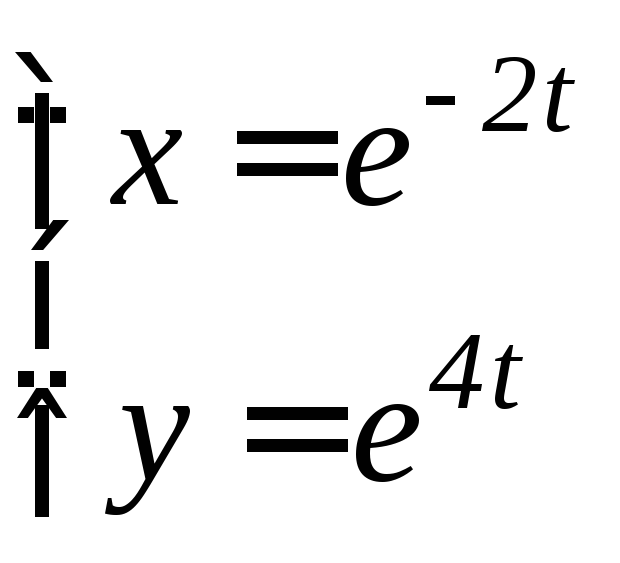Основные свойства дифференциала.

6.29 6.30 6.31

6.32 6.33 6.34

Дифференциал dy = f ^/(x) dx называется дифференциалом первого порядка.

Дифференциал d(dy) от дифференциала dy называется дифференциалом второго порядка функции f(x) и обозначается

d ² y, то есть d ²y= f ^//(x)(dx)² и т.д.

Дифференциал d(d ^n-1y) от дифференциала d ^n-1y называется дифференциалом n–го порядка функции f(x) и обозначается

d ⁿy, то есть d ⁿy= f ⁽ⁿ⁾(x)(dx)ⁿ.

Из определения производной и дифференциала вытекает, что y=dy+(x), где 0, когда x0, то есть дифференциал функции отличается от приращения на бесконечно малую высшего порядка, чем x=dx.

При малых x справедлива приближенная формула

f(x+x)–f(x)  f ^/(x)x или

f(x+x)  f ^/(x)x+ f(x) (6.29)

Пример 9. Найти дифференциал функции .

Решение. Так как dy = f ^/(x) dx, то .

Пример 10. Найти дифференциал функции y=sinlnx.

Решение. .

Пример 11. Найти дифференциал третьего порядка функции y = x⁵–3x³+2.

Решение. Последовательно дифференцируя, получим

.

Пример 12. Вычислить приближенное значение функции y = arcsinx при x = 0,51 .

Решение. Рассмотрим функцию y=arcsin x. Полагая x=0,5, x=0,01 и применяя формулу (6.29),

arcsin(x+x)  arcsin x+( arcsin x)^/ x, получаем

.

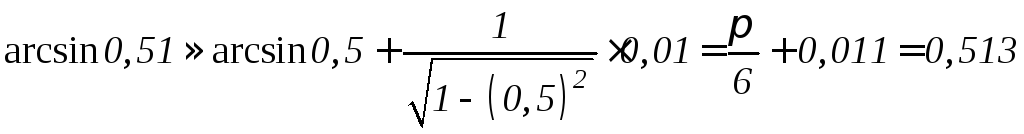Пример 13. Вычислить приближенное значение функции y = lnx при x = 2,001 .

Решение. Рассмотрим функцию y = lnx. Полагая x=2, x=0,001 и применяя формулу (6.29), , получаем

.

Задание 6.1. В задачах 1 - 30 вычислить производную y = f(x).

1.	1. 2. 3. 4. 5.	2.	1. 2. 3. 4. 5.
3.	1. 2. 3. 4. 5.	4.	1. 2. 3. 4. 5.
5.	1. 2. 3. 4. 5.	6.	1. 2. 3. 4. 5.
7.	1. 2. 3. 4. 5.	8.	1. 2. 3. 4. 5.
9.	1. 2. 3. 4. 5.	10.	1. 2. 3. 4. 5.
11.	1. 2. 3. 4. 5.	12.	1. 2. 3. 4. 5.
13.	1. 2. 3. 4. 5.	14.	1. 2. 3. 4. 5.
15.	1. 2. 3. 4. 5.	16.	1. 2. 3. 4. 5.
17.	1. 2. 3. 4. 5.	18.	1. 2. 3. 4. 5.
19.	1. 2. 3. 4. 5.	20.	1. 2. 3. 4. 5.
21.	1. 2. 3. 4. 5.	22.	1. 2. 3. 4. 5.
23.	1. 2. 3. 4. 5.	24.	1. 2. 3. 4. 5.
25.	1. 2. 3. 4. 5.	26.	1. 2. 3. 4. 5.
27.	1. 2. 3. 4. 5.	28.	1. 2. 3. 4. 5.
29.	1. 2. 3. 4. 5.	30.	1. 2. 3. 4. 5.

Задание 6.2. Продифференцировать данные функции, применяя метод логарифмического дифференцирования.

1.		2.
3.		4.
5.		6.
7.		8.
9.		10
11		12
13		14
15		16
17		18.
19	b)	20
21		22
23		24
25		26
27		28
29		30

Задание 6.3. Найти первую и вторую производные функций.

1.		2.
3.		4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.		26.
27.		28.
29.		30.

Задание 6.4. Вычислить с помощью дифференциала приближенное значение функции в заданной точке.

1.		2
3.		4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.		26.
27.		28.
29.		30.

72