
- •Производная функции
- •6.1 Дифференцирование функций, заданных явно
- •Основные правила дифференцирования.
- •Основные формулы дифференцирования.
- •6.2 Дифференцирование функций, заданных неявно
- •6.3 Дифференцирование функций, заданных параметрически Если функция y аргумента X задается при помощи параметрических соотношений
- •Дифференциал функции
- •Основные свойства дифференциала.
6.2 Дифференцирование функций, заданных неявно
Если yкак функция отx задается посредством соотношенияF(x,y)=0, гдеF(x,y) – выражение, содержащееx иy, тоyназываетсянеявной функциейотx. В некоторых случаях уравнениеF(x,y)=0 удается разрешить относительно y, и тогда можно перейти от неявного способа задания функции к явномуy=f(x), в других случаях такой переход невозможно осуществить. Независимо от возможности перехода производная отy поxдля функции, заданной неявно, может быть определена следующим образом:
Находим производную от левой части равенства F(x,y)=0, учитывая при этомyкак функцию отx, и приравниваем ее к нулю.
2. Разрешаем полученное уравнение относительноy/; в результате будем иметь выражение производной от неявной функции в видеy/=f(x,y). Для определения второй производной от функции, заданной неявно, дифференцируем равенствоy/=f(x,y) (рассматриваяyкак функцию отx), а затем в правой части заменяемy/его выражением из равенстваy/=f(x,y). Аналогично поступаем при нахождении производных более высоких порядков.
Пример 7. Найти y// , если arctg y – y + x = 0.
Решение.
Дифференцируем данное выражение,
рассматривая y
как функцию от x
:
![]()
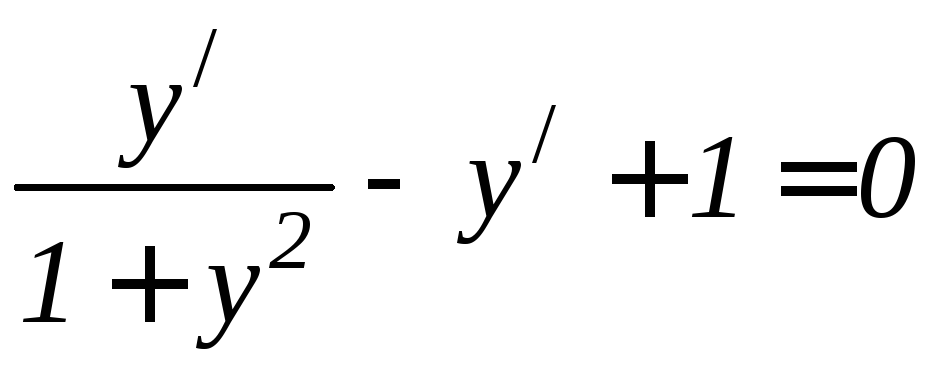 или
или
![]() ,
,![]() ,
,
![]() ,
,
откуда
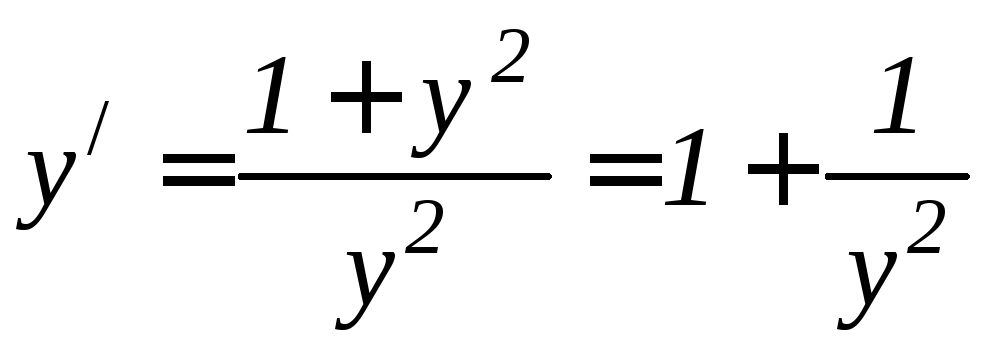 .
.
Находим
далее y//: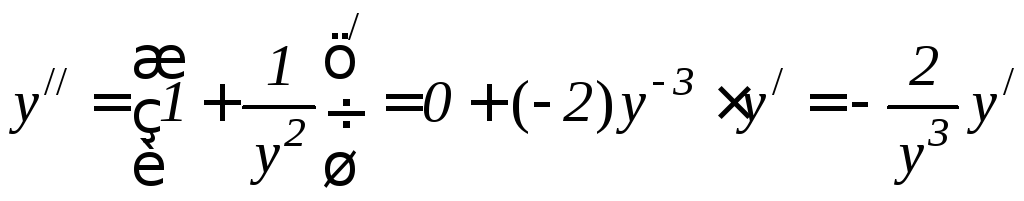 .
.
В
последнее равенство вместо y/
подставляем его значение. Тогда получаем
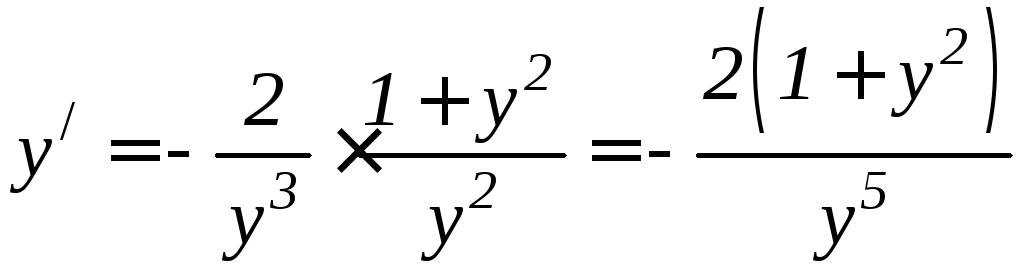 .
.
6.3 Дифференцирование функций, заданных параметрически Если функция y аргумента X задается при помощи параметрических соотношений
x= x(t), y= y(t) (6.27)
причем x(t) и y(t) – дифференцируемые функции t и x(t)0. Производная от y по x находится путем дифференцирования равенств (1) :
dx=x/(t)dt , dy=y/(t)dt,
откуда
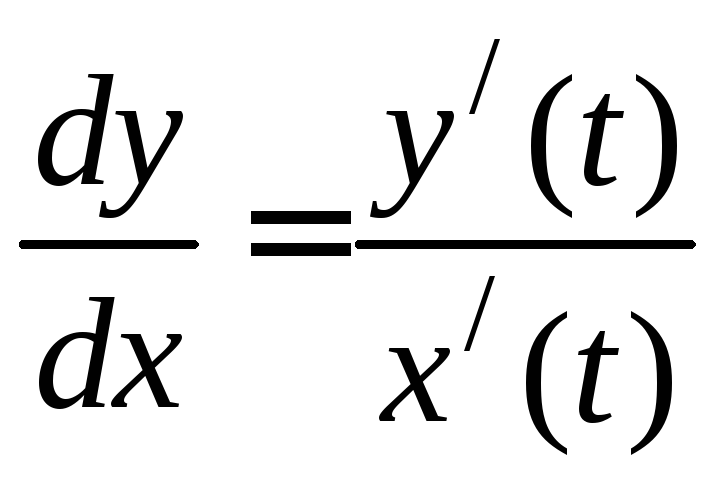 .
(6.28)
.
(6.28)
Вторую производную от y по x находим, дифференцируя по x соотношение (6.28):
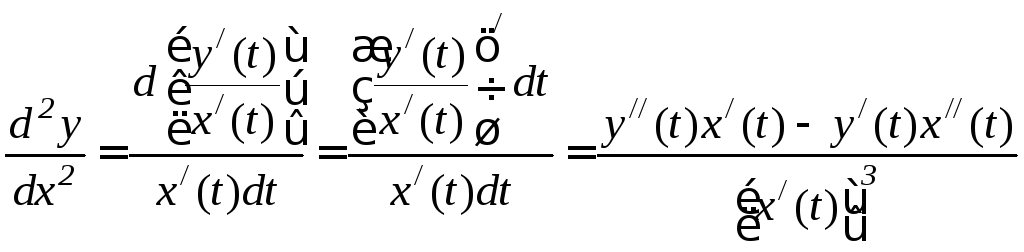 .
.
Пример
6.8 Найти
![]() ,
если x=ln
t,
y=sin
2t.
,
если x=ln
t,
y=sin
2t.
Решение. Дифференцируем исходные соотношения:
![]() ,
,
![]() .
.
Отсюда
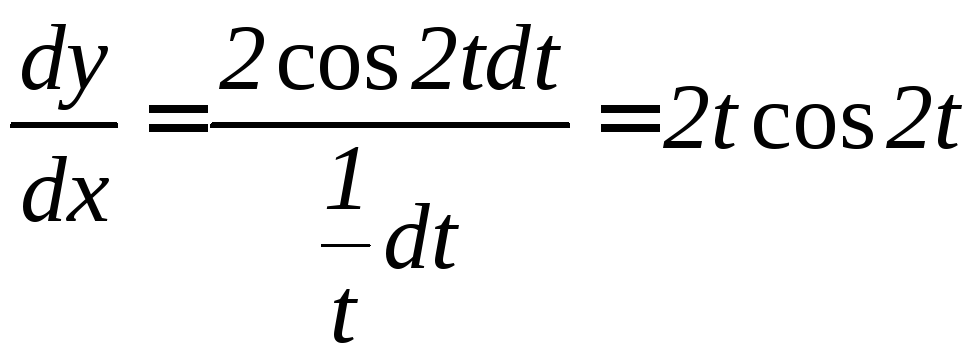 .
.
Найдем вторую производную
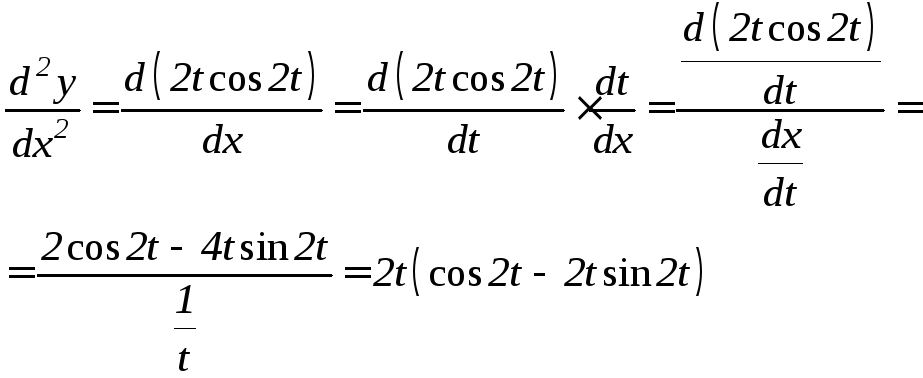 .
.
Дифференциал функции
Пусть функция y= f(x) дифференцируема на отрезке [a,b]. Производная этой функции в некоторой точке x отрезка [a,b] определяется равенством
![]() .
.
Отношение
![]() при
x0
стремится к определенному числу f
/(x)
и, следовательно, отличается от
производной f
/(x)
на величину бесконечно малую:
при
x0
стремится к определенному числу f
/(x)
и, следовательно, отличается от
производной f
/(x)
на величину бесконечно малую:
![]() ,
где0
при
x
0,
,
где0
при
x
0,
или y= f /(x)x + x.
Таким образом, приращение функции y представляет собой сумму двух слагаемых f /(x)x и x, которые являются бесконечно малыми при x0. Первое слагаемое есть бесконечно малая функция первого порядка относительно x, так как
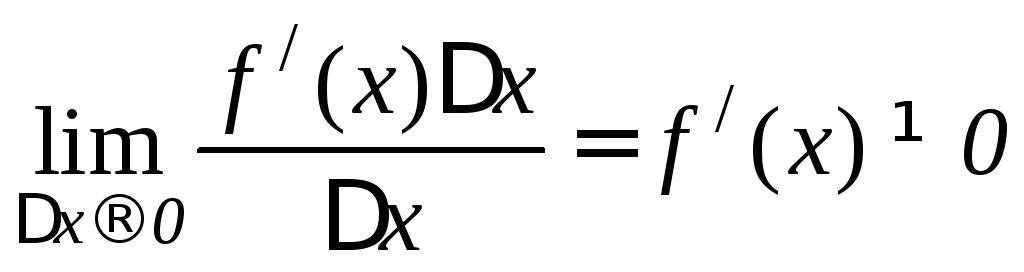 .
.
Произведение x есть бесконечно малая величина высшего порядка относительно x, так как
![]() .
.
Первое слагаемое f /(x)x называется главной частью приращения функции y.
Дифференциалом функции y= f(x) в точке называется главная часть ее приращения, равная произведению производной f /(x) на приращение x и обозначается через dy:
dy = f /(x) x .
Дифференциалом аргумента называется приращение аргумента
dx = x.
Тогда дифференциал функции равен произведению ее производной на дифференциал аргумента dy = f /(x) dx.
Геометрически дифференциал представляет собой приращение ординаты касательной к графику функции в точке M(x,y).
