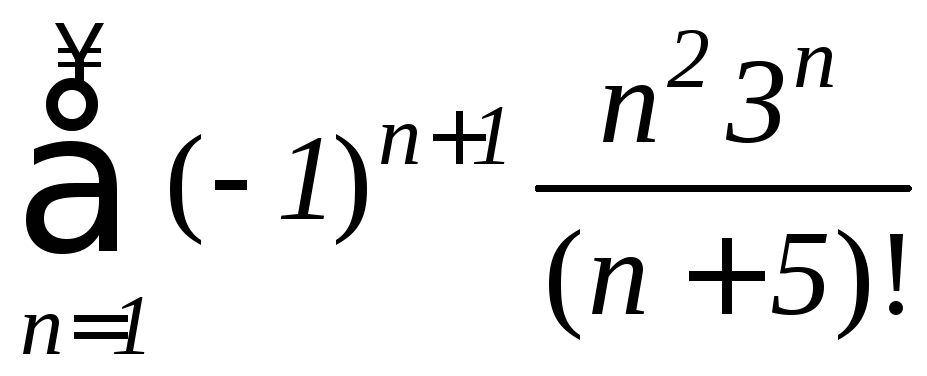13.3. Ряды Фурье и интегралы Фурье
Если на интервале [-,] функция f(t) удовлетворяет условию Дирихле: функция непрерывна с конечным числом экстремумов или имеет конечное число точек разрыва первого рода - то ряд Фурье этой функции сходится в точках непрерывности к самой функции f(t), а в точках разрыва первого рода - к полусумме левого и правого пределов функции f(t).
 ,
где n=1,2,3,…
,
,
где n=1,2,3,…
,
 ;
;
 ;
; .
.
Если функция f(t) периодична с периодом 2, удовлетворяет условию Дирихле, то ряд Фурье данной функции сходится к ней для любого t. То же самое относится и к случаям, если функция f(t) периодична с периодом T или 2l. Соответствующие формулы имеют вид:
 ,
,
где
 ;
; ;
;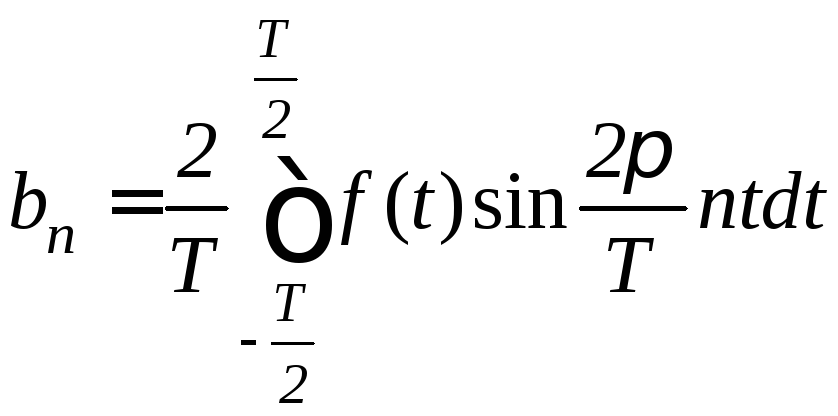 .
.
 ,
,
где
 ;
; ;
;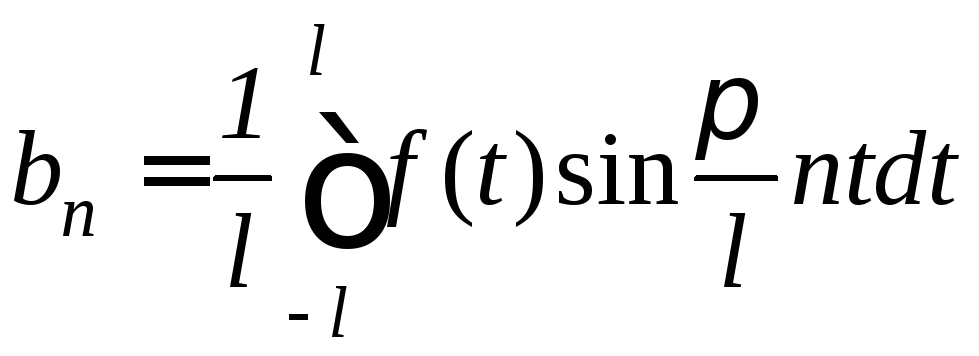 .
.
Если
функция f(t)
четная, то
![]() ;
если нечетная
;
если нечетная![]() и ряд Фурье упрощается.
и ряд Фурье упрощается.
Если f(t) задана на полуинтервале, то ее можно разложить в ряд Фурье по косинусам или синусам, продлив функцию соответственно четным или нечетным образом на весь период.
Если
рядом Фурье представлялась функция
![]() периодическая или заданная на периоде
и удовлетворяющая условиям Дирихле на
этом периоде, тоинтегралом
Фурье
представляется функция
периодическая или заданная на периоде
и удовлетворяющая условиям Дирихле на
этом периоде, тоинтегралом
Фурье
представляется функция
![]() непериодическая, к которой предъявляются
два условия:
непериодическая, к которой предъявляются
два условия:
должна быть кусочно-гладкая, т.е. должна быть на некотором интервале непрерывной и иметь непрерывную производную во всех точках этого интервала , за исключением, быть может, конечного числа точек, в которых функция имеет разрыв 1 рода (это аналог условия Дирихле);
должна быть абсолютно интегрируема на всей числовой оси, т.е. должен быть сходящимся
 На электротехническом языке это
означает одиночный импульс тока или
напряжения, имеющий начало и конец.
На электротехническом языке это
означает одиночный импульс тока или
напряжения, имеющий начало и конец.
Тогда
функция
![]() представляется несколькими видами
интеграла Фурье:
представляется несколькими видами
интеграла Фурье:
а)

где
 .
.
Здесь
![]() и
и![]() - одна и та же функция с аргументамиx
и t.
В частных случаях
- одна и та же функция с аргументамиx
и t.
В частных случаях
![]() может быть четной и нечетной.
может быть четной и нечетной.
Если
![]() - чётная, то
- чётная, то![]() и тогда
и тогда
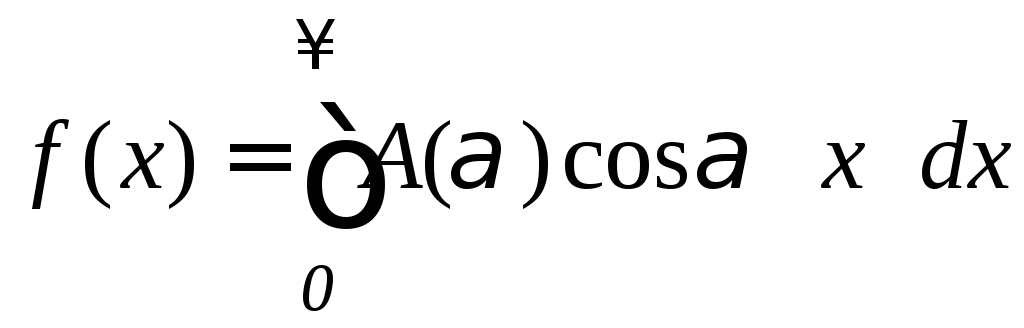 ,
где
,
где
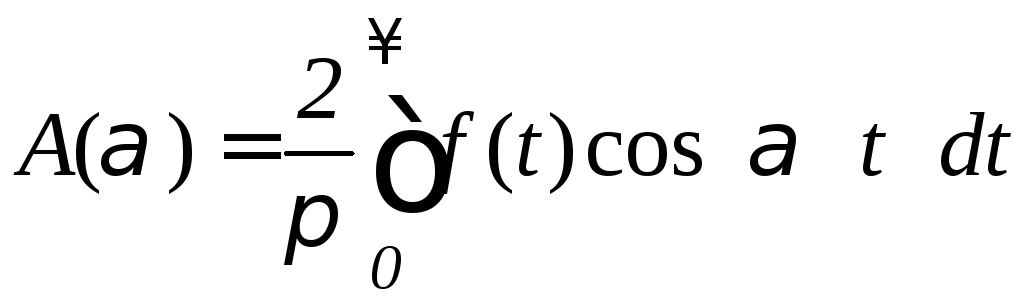 .
.
Иногда
вводят функцию
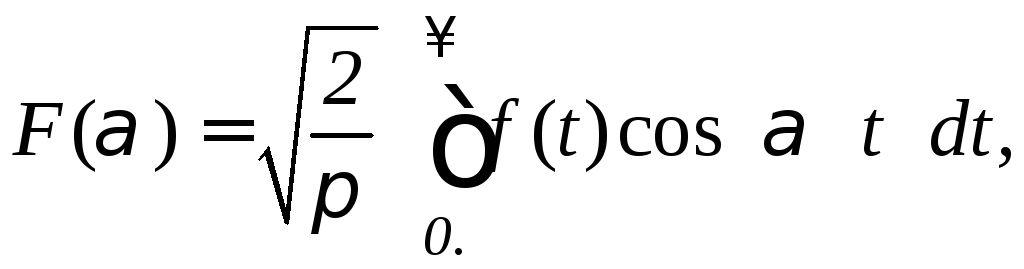
тогда
 В этом случае функцию
В этом случае функцию![]() называюткосинус-
преобразованием Фурье.
называюткосинус-
преобразованием Фурье.
Если
![]() - -нечетная, то
- -нечетная, то![]() и тогда
и тогда
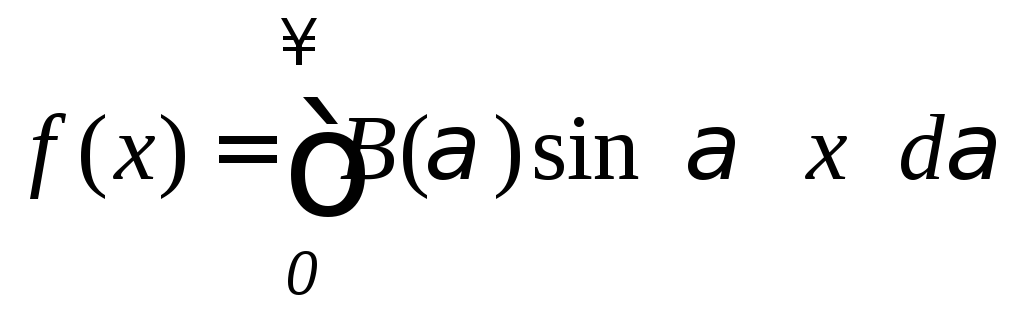 ;
;

Если ввести функцию
 -
синус-преобразование
Фурье,
-
синус-преобразование
Фурье,
то
 .
.
Второй вид интеграла Фурье :
 .
.
с) Третий вид интеграла Фурье – в комплексной форме – здесь не рассматривается.
Представить
функцию
![]() интегралом Фурье значит:
интегралом Фурье значит:
Вид а) -
найти функцию
![]() и
и![]() или
или![]() или
или![]() и подставить в соответствующую формулу.
и подставить в соответствующую формулу.
Вид b)
- посчитать внутренний интеграл и подставить в формулу.
и подставить в формулу.
Пример
13. Разложить
функцию
![]() в ряд Фурье на интервале (-,).
в ряд Фурье на интервале (-,).
Решение. Продолжим функцию периодическим образом с периодом 2 ( рис. 13.1. ).



![]()



![]()











 -
-![]()
![]() t
t

-![]()
Рис. 13.1.
Функция
![]() нечетная, поэтому коэффициенты
нечетная, поэтому коэффициенты![]() .
.



Ряд
Фурье:
 .
.
Равенство справедливо всюду, кроме точек разрыва (на концах интервала), где ряд сходится к 0, т.к. сумма ряда равна :
 .
.
Пример 14
. Разложить
в ряд Фурье функцию
.
.
Пример 14
. Разложить
в ряд Фурье функцию
 на интервале (,).
на интервале (,).
Решение. Продолжим функцию периодическим образом с периодом 2π (рис.13.2.)





Рис. 13.2.
Функция
 четная, поэтому коэффициент
четная, поэтому коэффициент![]() .
.
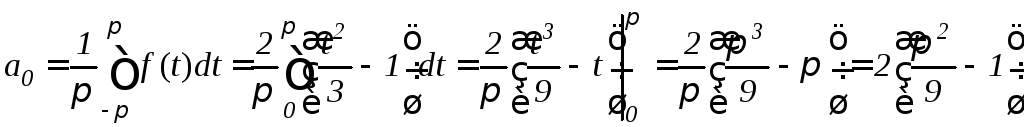


Ряд
Фурье:
 .
.
Пример
15. Разложить
в ряд Фурье функцию
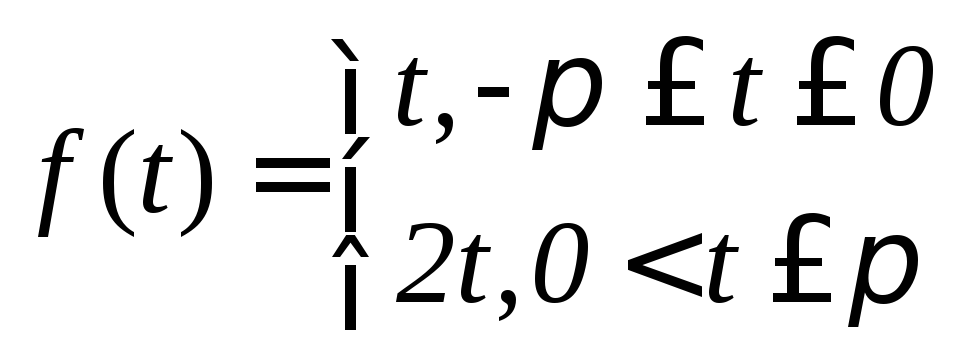 .
.
Решение. Продолжим функцию периодическим способом с периодом 2π (рис. 13.3.)

Рис.13.3.
 .
.


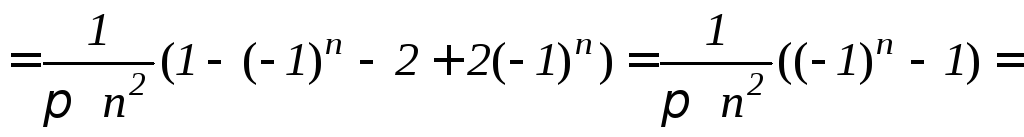

 ;
k=0,1,2,…
;
k=0,1,2,…


Ряд Фурье:

Пример
16. Разложить
функцию
![]() на интервале
на интервале![]() ;
;![]() в ряд косинусов.
в ряд косинусов.
Решение.
Чтобы в
разложении были только косинусы,
необходимо иметь четную функцию, поэтому
продолжим функцию
![]() на интервале
на интервале![]() ;
;![]() четным, периодическим образом ( рис.
13.4.) .
четным, периодическим образом ( рис.
13.4.) .
 f(t)
f(t)
![]()
t
![]()
![]()
![]() 0
0
![]()
![]()
Рис. 13.4.



![]()

Чтобы
разложить ту же функцию
![]() на интервале
на интервале![]() в ряд синусов, нужно продолжить эту
функцию нечетным, периодическим образом
(рис.13.5.).
в ряд синусов, нужно продолжить эту
функцию нечетным, периодическим образом
(рис.13.5.).


Рис. 13.5.
![]()

![]()
 Еще
раз обратим внимание на то, что указанные
в примерах функции раскладываются в
соответствующий ряд Фурье только в
указанных интервалах. За пределами
интервалов этого разложения нет.
Еще
раз обратим внимание на то, что указанные
в примерах функции раскладываются в
соответствующий ряд Фурье только в
указанных интервалах. За пределами
интервалов этого разложения нет.
Если
интервалы заданы
![]() или
или![]() ,
то разложение в ряд Фурье производят
по приведенным выше формулам.
,
то разложение в ряд Фурье производят
по приведенным выше формулам.![]()
Пример
17. Найти
косинус-преобразование Фурье и написать
интеграл Фурье для функции:
 (рис.13.6).
(рис.13.6).
Решение. Построим график функции (рис. 13.6.)

Рис.13.6.
Проверим функцию f(x) на абсолютную интегрируемость:
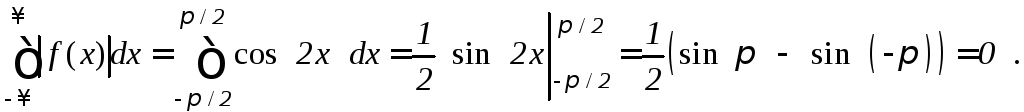 Несобственный
интеграл существует и конечен, значит
f(x)
абсолютно интегрируема на всей числовой
оси.
Несобственный
интеграл существует и конечен, значит
f(x)
абсолютно интегрируема на всей числовой
оси.
Найдем косинус-преобразование :



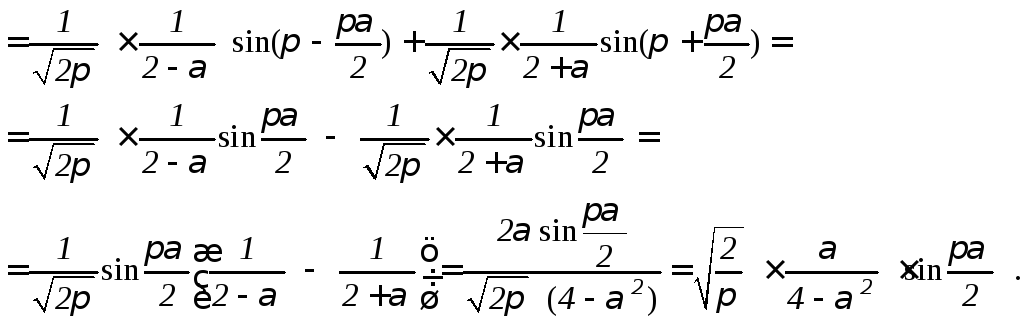
Интеграл Фурье для функции:

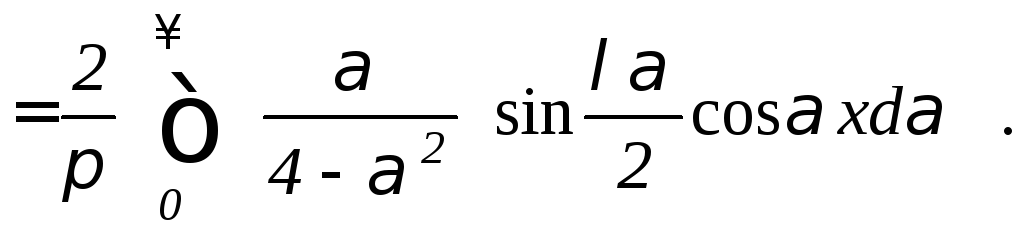
Задание 13.1. Исследовать на сходимость числовые ряды (для знакочередующихся рядов провести исследование на абсолютную и условную сходимость).
1.
-
а)

б)

в)

г)

д)

е)

2.
-
а)

б)

в)

г)

д)

е)

3.
-
а)
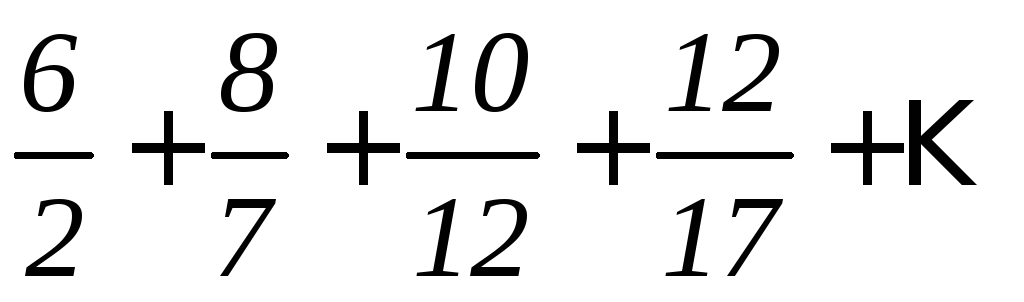
б)

в)

г)

д)

е)

4.
-
а)

б)

в)

г)

д)
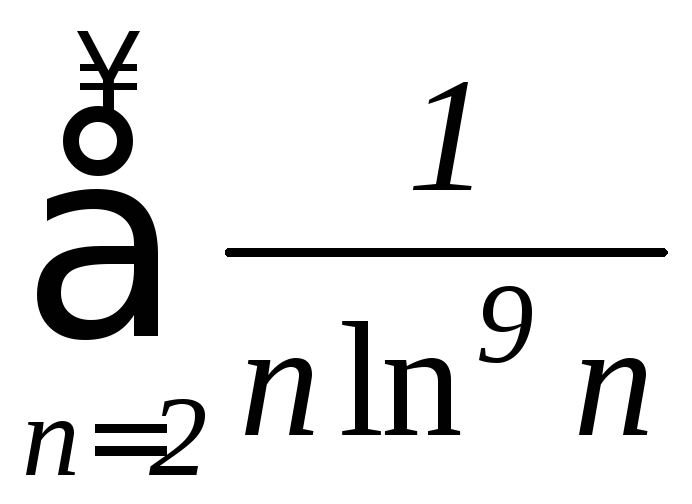
е)

5.
-
а)

б)

в)

г)

д)

е)

6.
-
а)

б)

в)

г)

д)

е)

7.
-
а)

б)

в)

г)
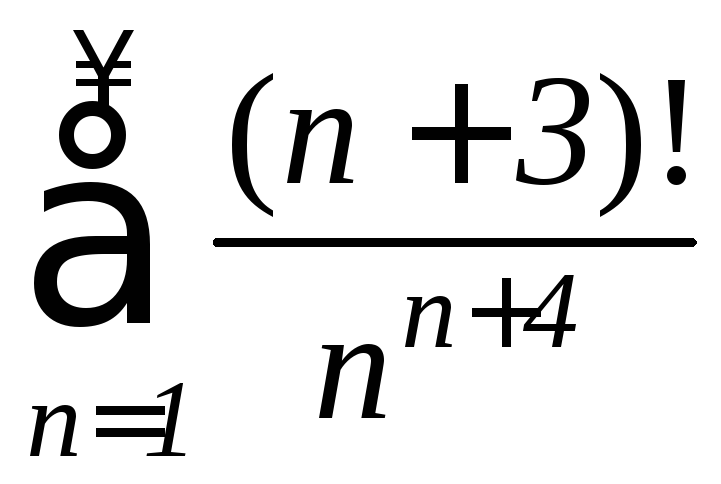
д)

е)

8.
-
а)

б)

в)

г)
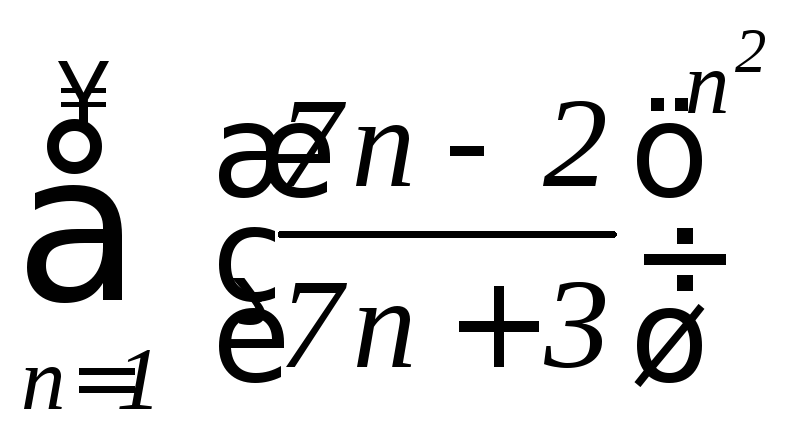
д)

е)

9.
-
а)

б)

в)
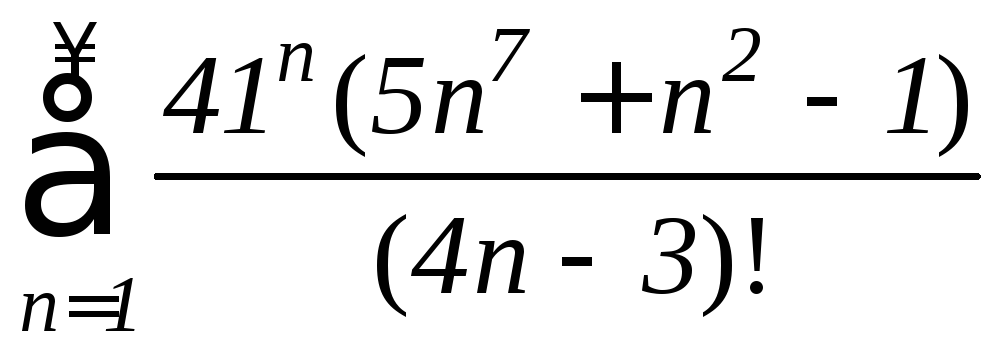
г)

д)

е)

10.
-
а)

б)

в)

г)

д)

е)
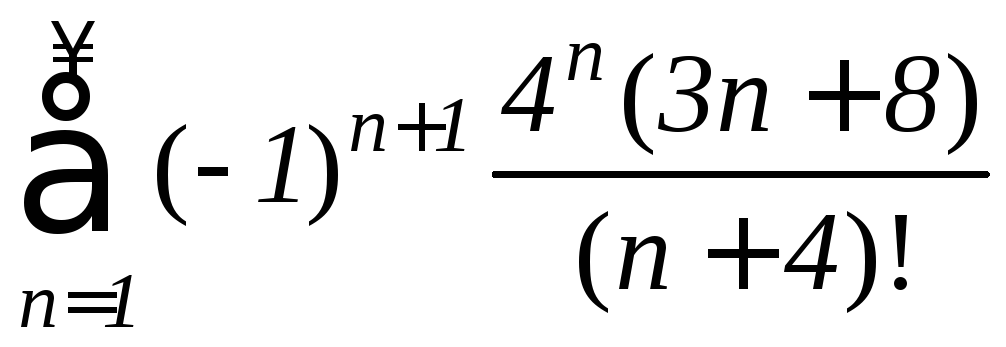
11.
-
а)

б)

в)

г)

д)

е)

12.
-
а)

б)

в)

г)

д)

е)

13.
-
а)
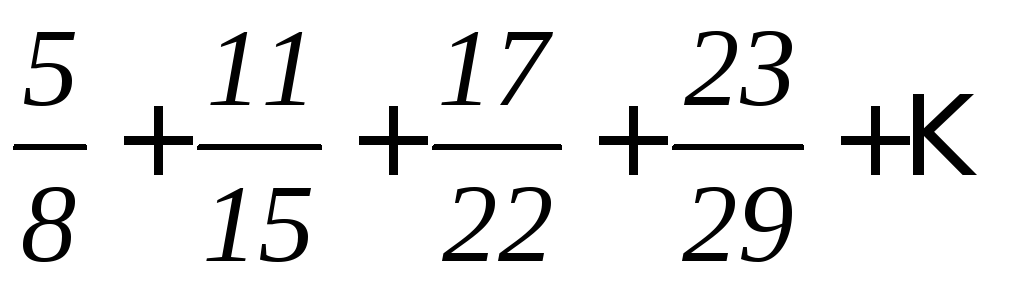
б)

в)

г)

д)

е)

14.
-
а)

б)

в)

г)

д)

е)

15.
-
а)

б)

в)

г)

д)

е)

16.
-
а)

б)
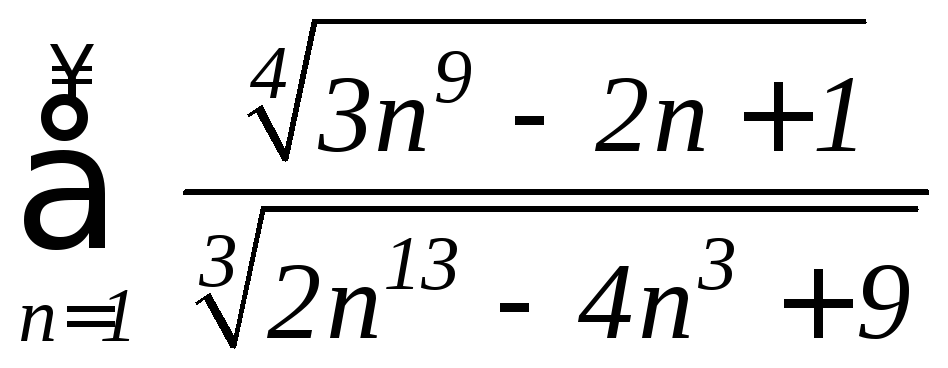
в)

г)

д)

е)

17.
-
а)

б)

в)
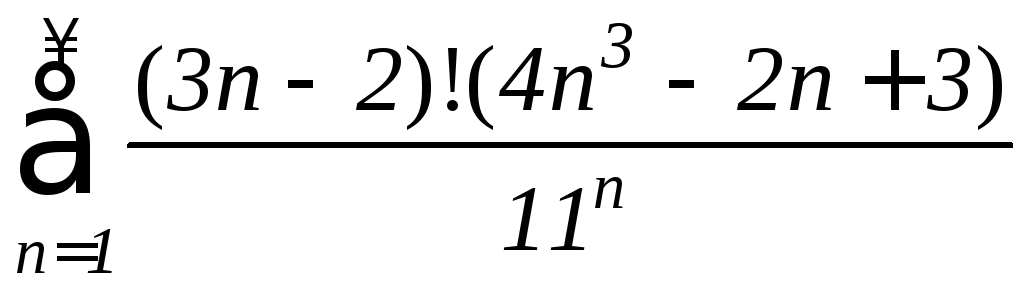
г)
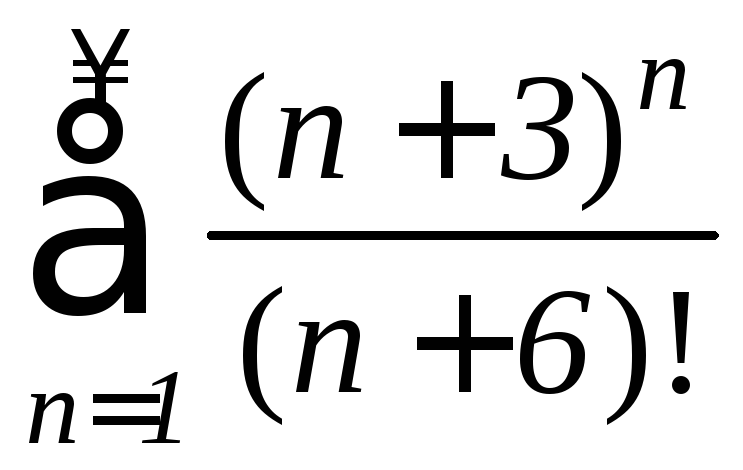
д)

е)

18.
-
а)

б)

в)

г)

д)

е)

19.
-
а)

б)

в)

г)

д)

е)

20.
-
а)
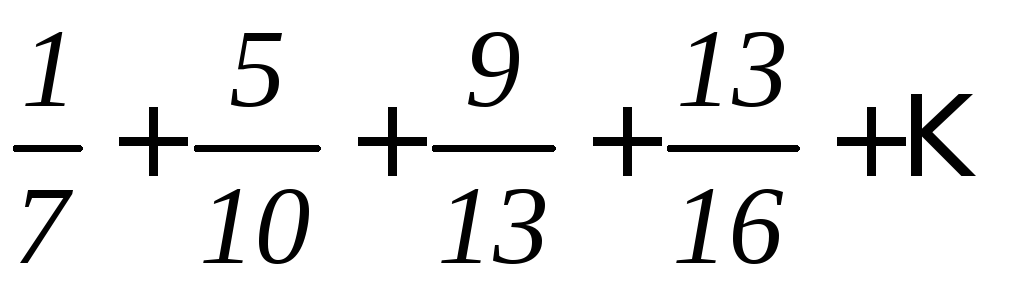
б)
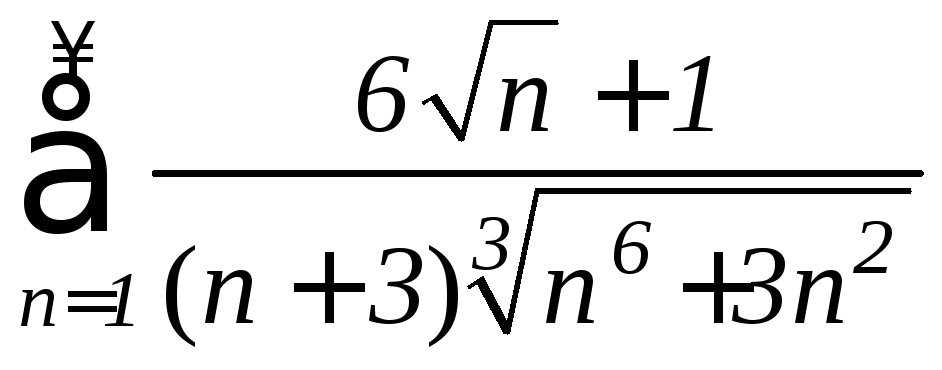
в)

г)

д)

е)

21.
-
а)

б)

в)

г)

д)

е)

22.
-
а)

б)
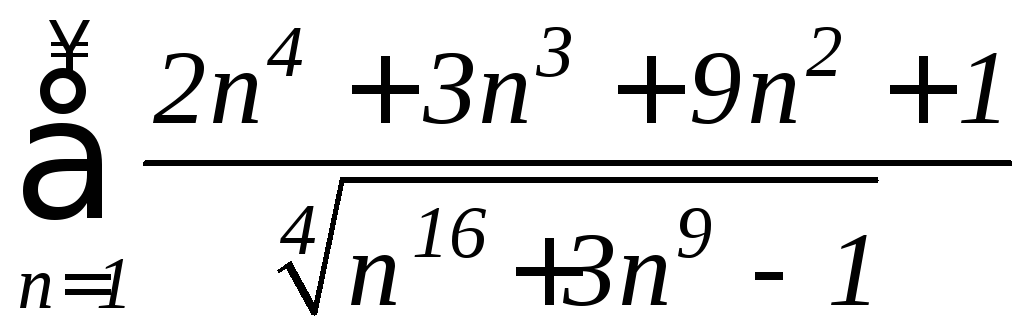
в)

г)

д)

е)

23.
-
а)

б)
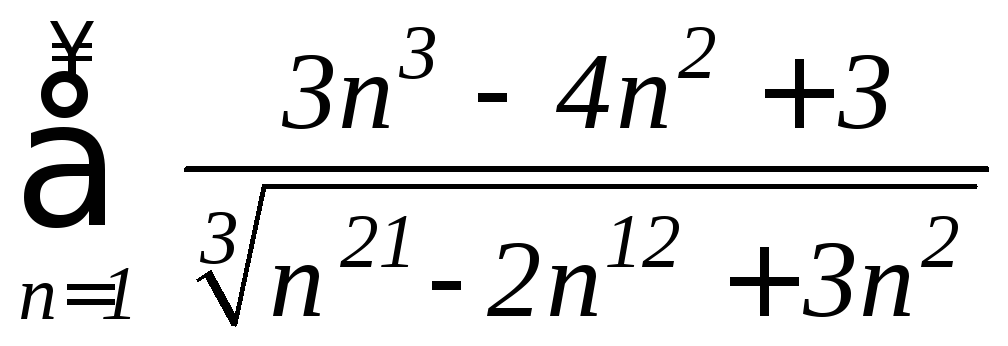
в)

г)

д)
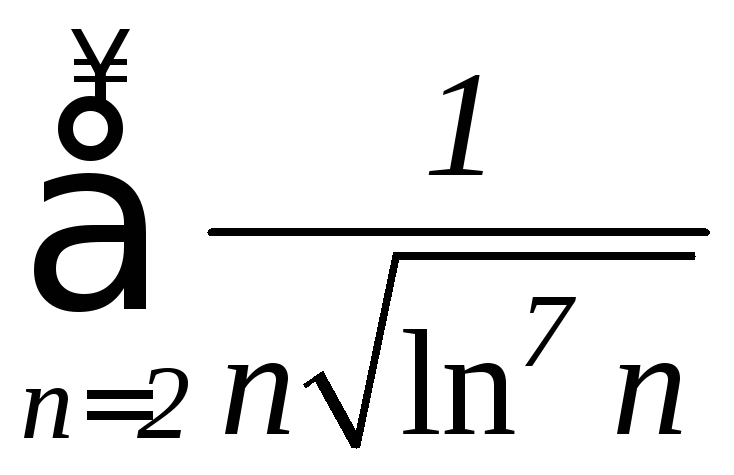
е)

24.
-
а)

б)

в)

г)

д)
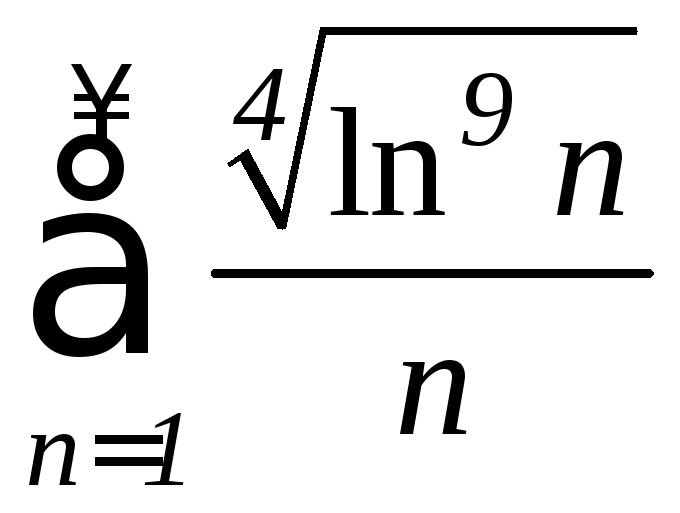
е)

25.
-
а)

б)

в)

г)

д)

е)