13. Ряды

1. Числовые ряды

1. Числовым рядом называется выражени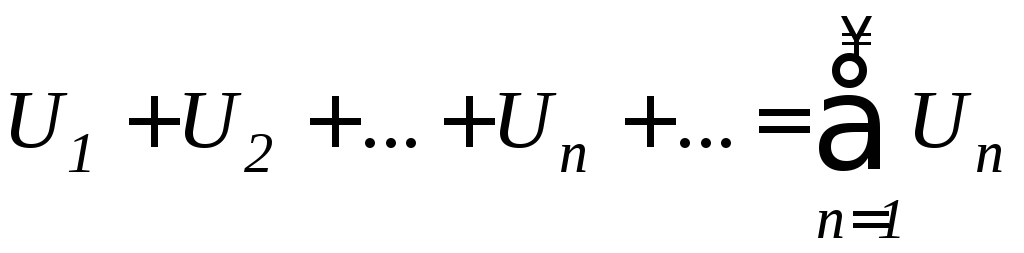е , где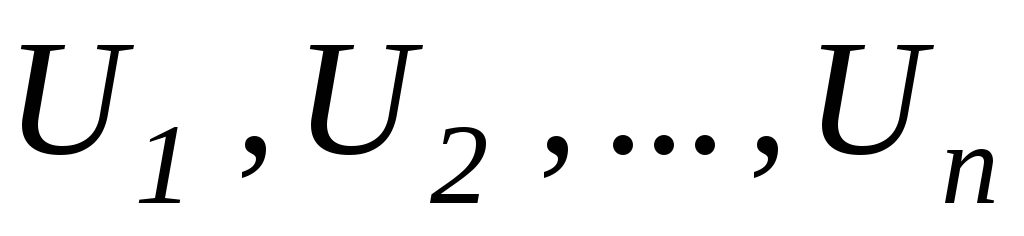- числовая последовательность. Числовой ряд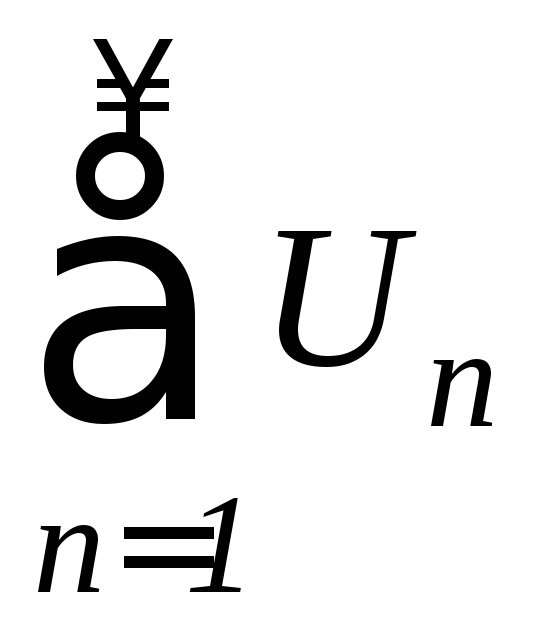называетсясходящимся, если существует 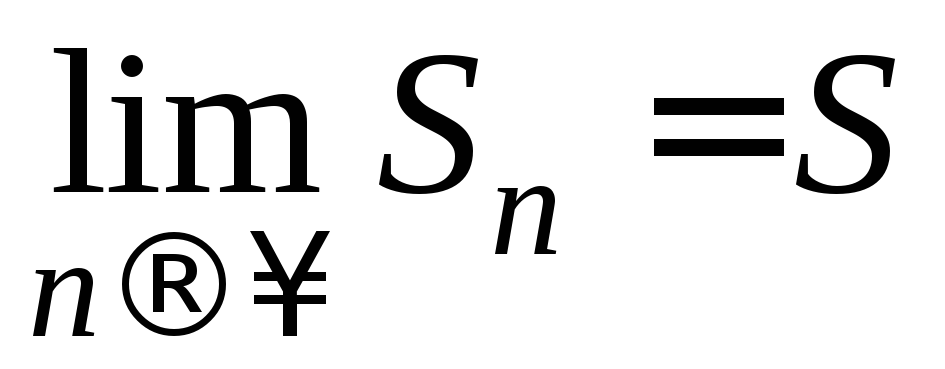, где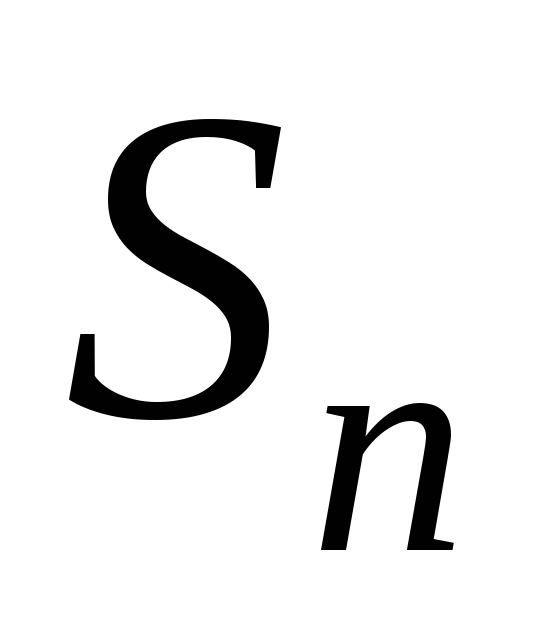- частичная сумма,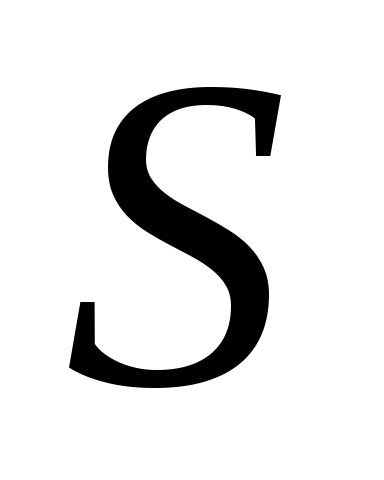- сумма ряда.

Необходимый признак сходимости: если ряд 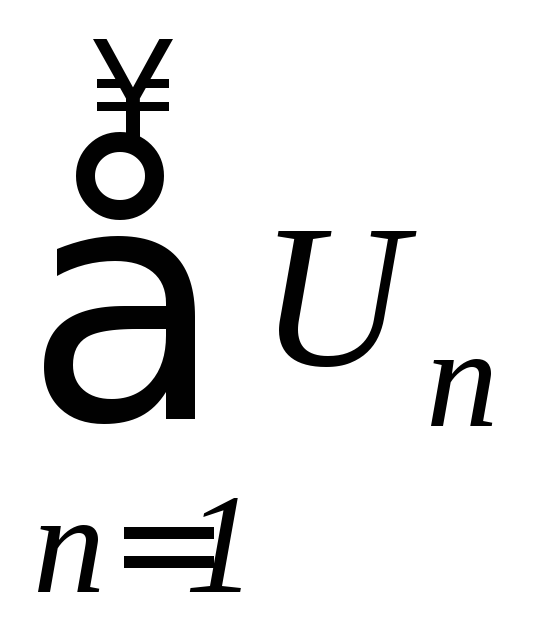сходится, то предел его общего члена приn равен нулю: . Обратное утверждение неверно. Если этот предел не равен0, то ряд расходится.

Достаточные признаки сходимости знакоположительных рядов.

1. Признак сравнения.

Если даны два ряда (1.1) и(1.2), общие члены которых удовлетворяют соотношению, то из сходимости ряда (1.2) следует сходимость ряда (1.1) и из расходимости ряда (1.1) следует расходимость ряда (1.2).

На практике используется предельный признак сравнения.

Если существует 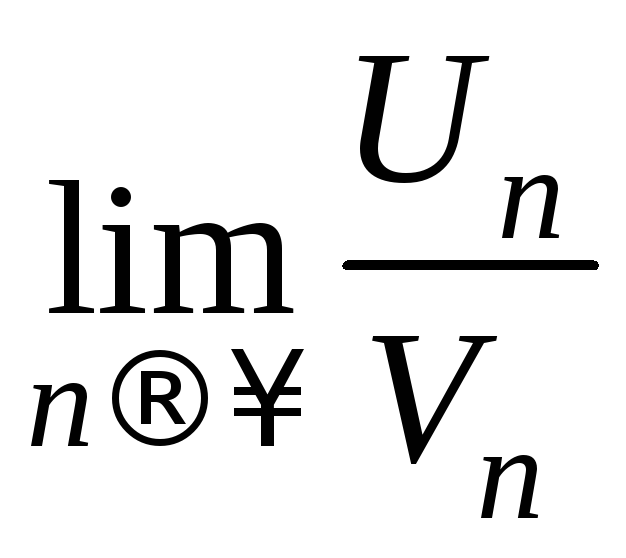конечный, отличный от нуля, то оба ряда либо сходятся, либо расходятся одновременно.

В качестве образцового ряда берут ряд Дирихле 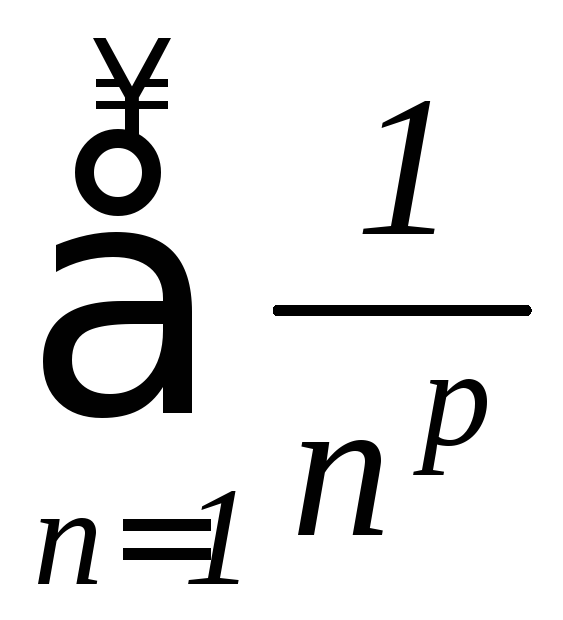, который прирасходится, а при- сходится.

2. Признак Даламбера.

Если для ряда 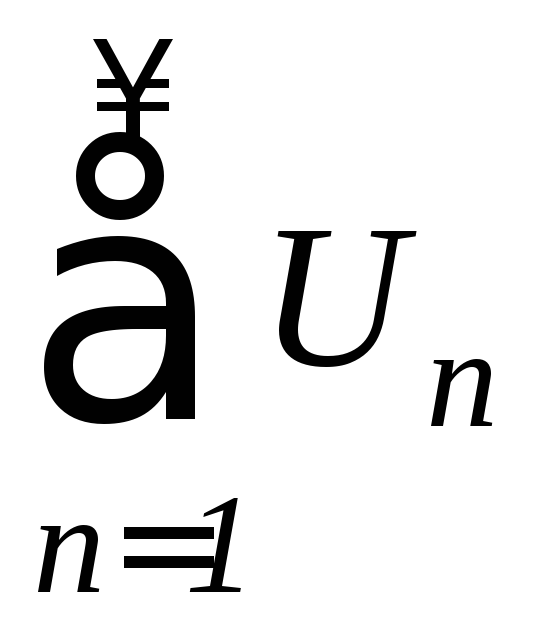существует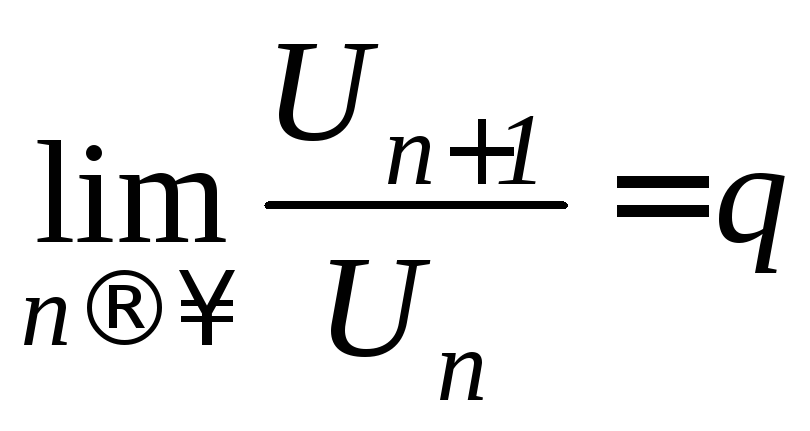, то приряд сходится, при- расходится, при- неопределенность.

3. Радикальный признак.

Если для ряда существует, то приряд

сходится, при - расходится, при- неопределенность.

4. Интегральный признак сходимости.

Если существует функция f(x), для которой f(n)=U_n , где U_n- общий член ряда 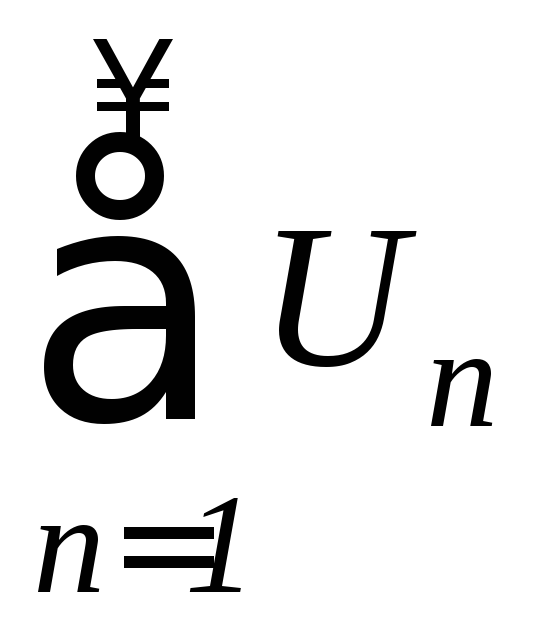, то данный ряд и интеграл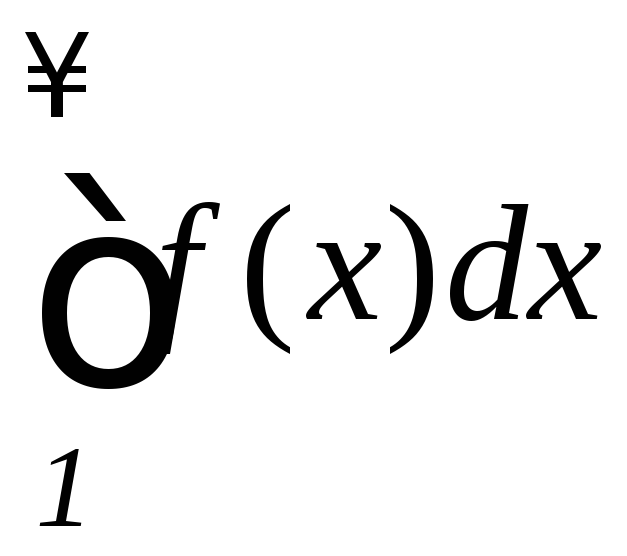сходятся и расходятся одновременно.

5. Признак сходимости знакочередующегося ряда.

Если члены знакочередующегося ряда 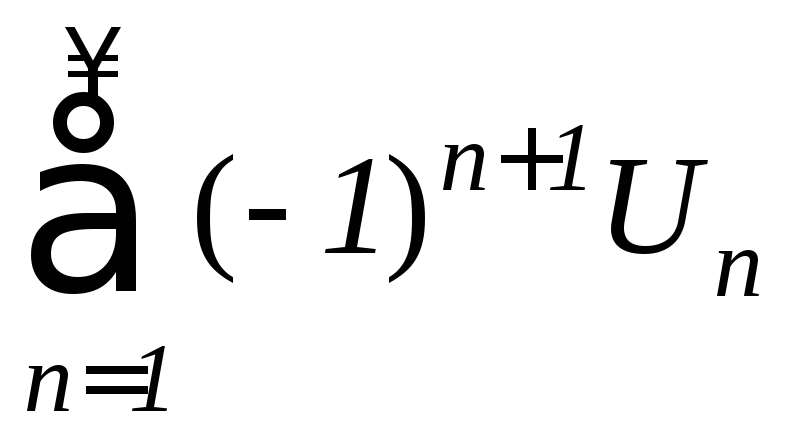удовлетворяют условиям:

2. ,

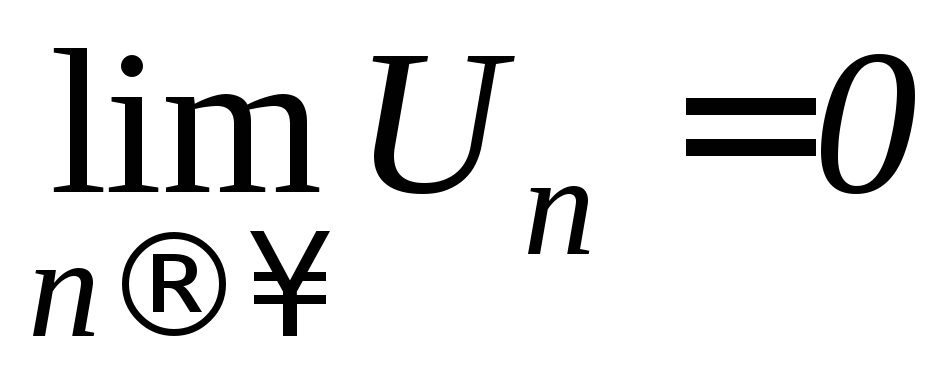то ряд сходится, его сумма положительна и не превосходит первого члена U₁, то есть .

Если в знакочередующемся ряде ограничить сумму n членами, то ошибка, совершаемая при замене суммы ряда на частичную сумму, не превосходит абсолютной величины первого из отброшенных членов.

Пример 1. Исследовать на сходимость ряд .

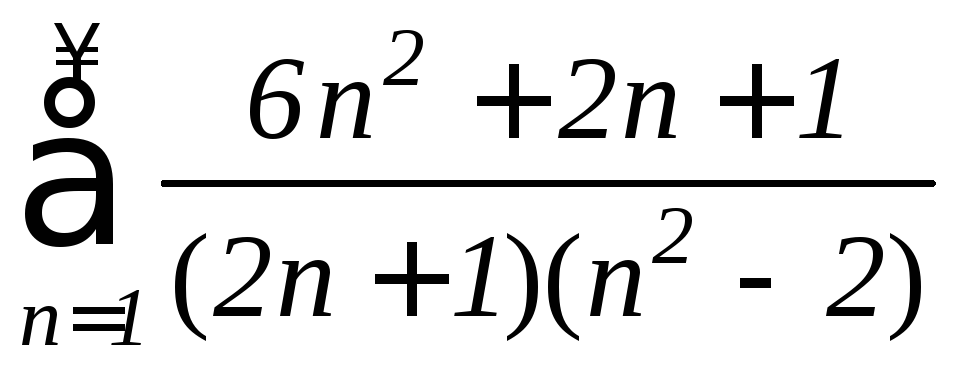Решение. Проверим выполнение необходимого признака .

.

Признак выполняется. Требуется продолжить исследования по достаточным признакам. Применим предельный признак сравнения. В качестве известного ряда возьмем гармонический ряд , который расходится, так как.

,

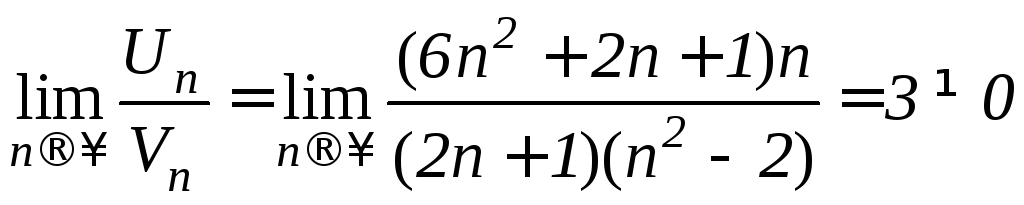значит исследуемый ряд расходится.

Пример 2. Исследовать на сходимость ряд .

Решение. Проверка выполнения необходимого признака потребует громоздких вычислений (применение формулы Стирлинга), поэтому применим один из достаточных признаков. Если в общем члене ряда содержится факториал, то лучше применить признак Даламбера.

;

.

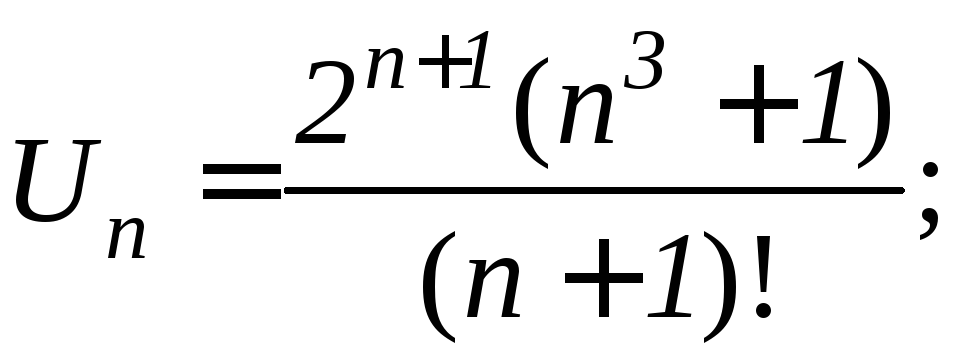
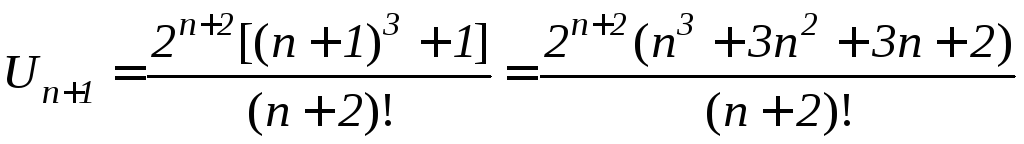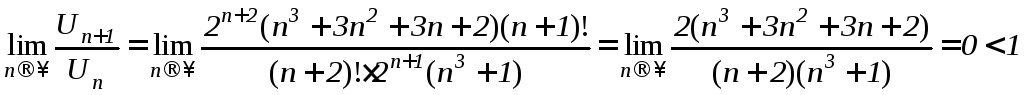Ряд сходится.

Пример 3. Исследовать на сходимость ряд .

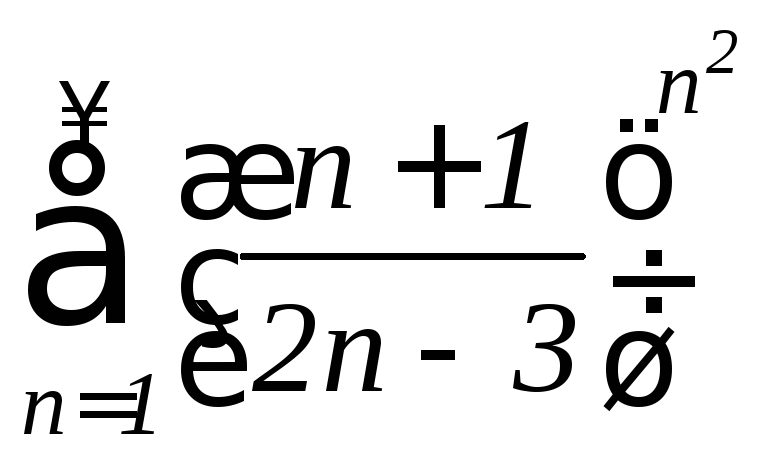Решение. По необходимому признаку получаем:

.

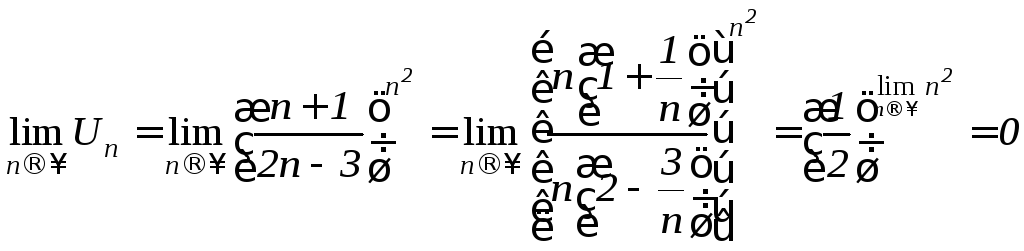Из общего члена ряда легко извлечь корень n-ой степени, поэтому применим радикальный признак Коши:

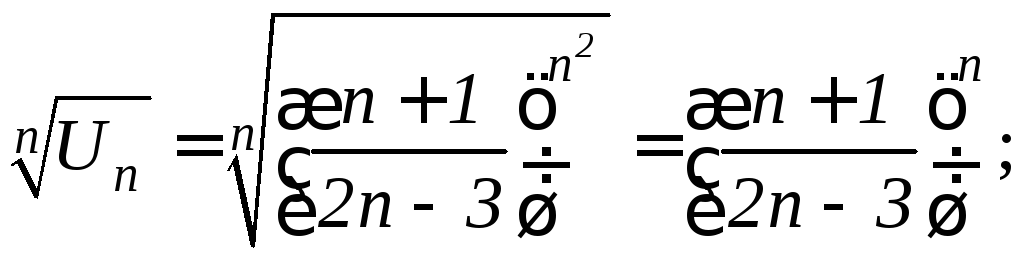
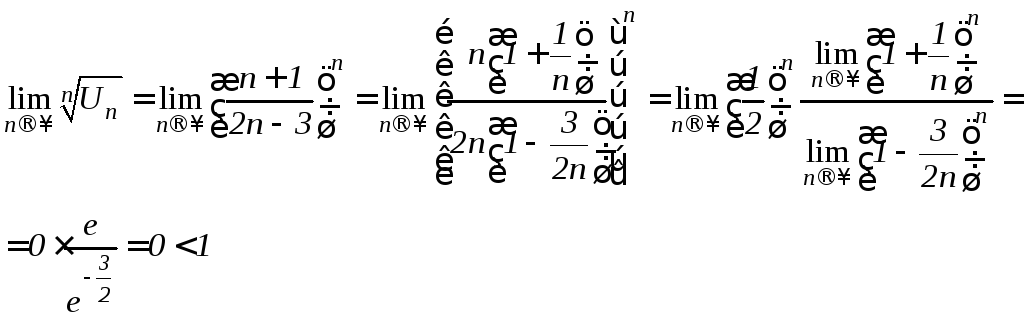
Ряд сходится.

Пример 4. Исследовать на сходимость ряд .

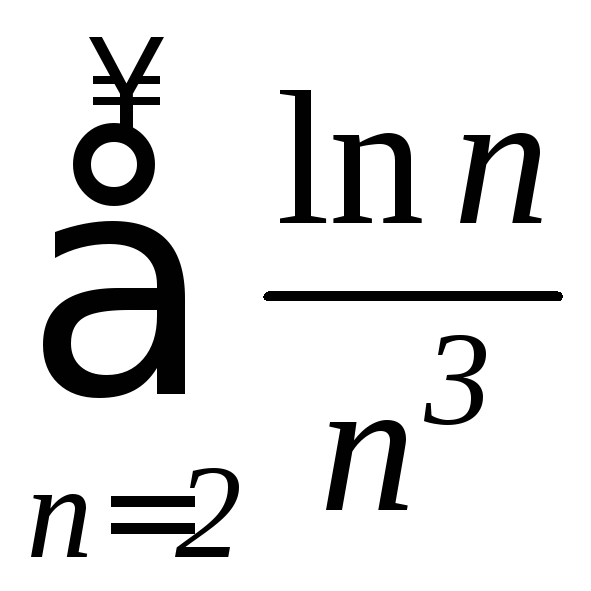Решение. Необходимый признак:

.

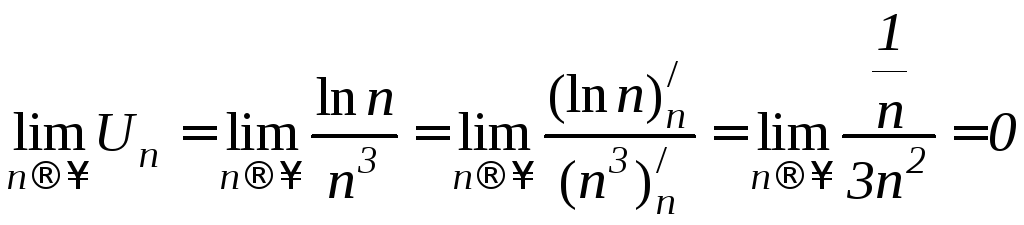Применим интегральный признак.

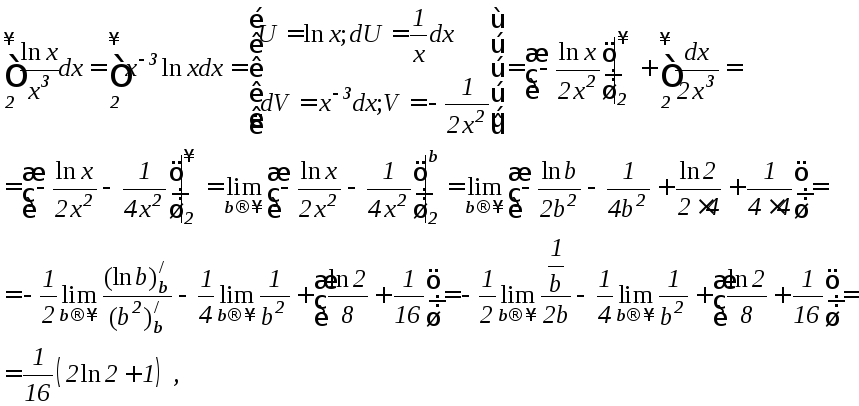несобственный интеграл сходится, значит и ряд сходится.

Пример 5. Исследовать на сходимость ряд .

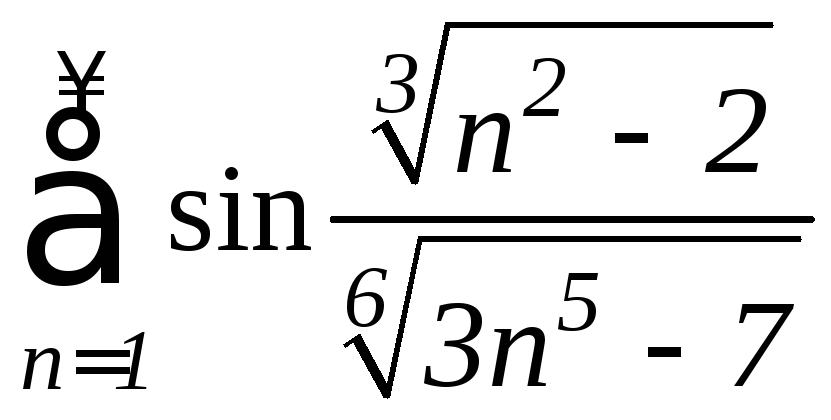Решение.Необходимый признак:

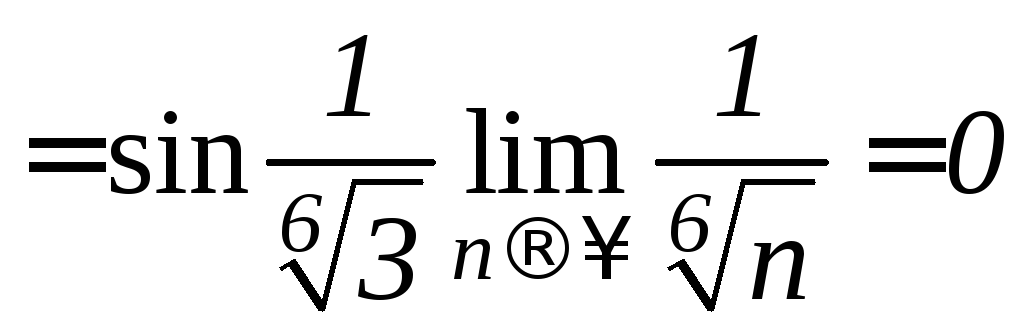
Для исследования ряда применим предельный признак сравнения дважды.

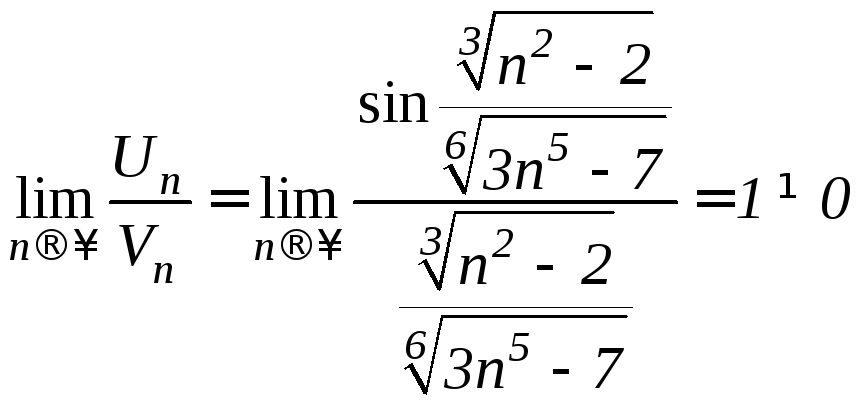- (по первому замечательному пределу),

, где

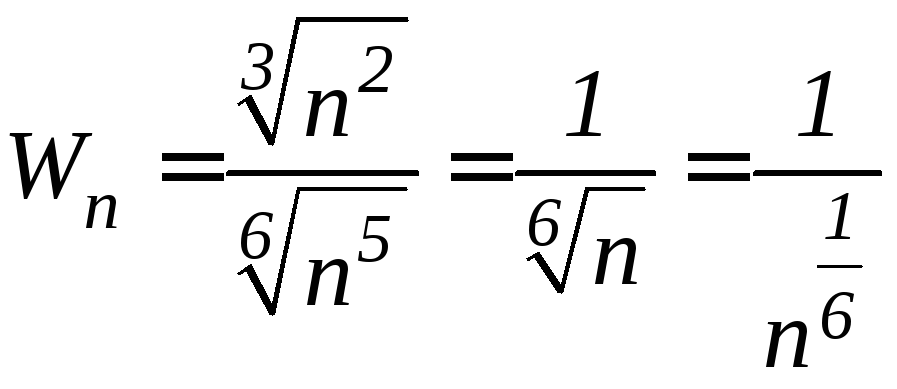- ряд Дирихле, . Все ряды расходятся.

Пример 6. Исследовать на сходимость ряд .

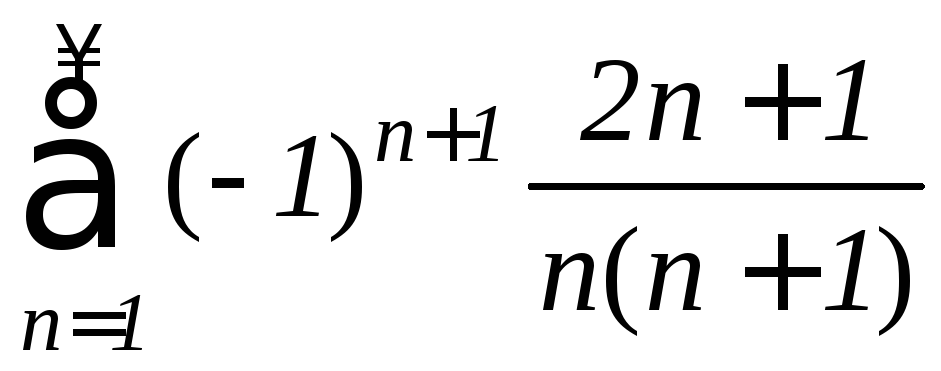Решение. По признаку Лейбница для знакочередующегося ряда:

, ряд сходится.

Исследуем ряд на абсолютную сходимость по признаку сравнения.

.

Ряд абсолютно расходится, т.к. гармонический ряд - расходится.

Знакопеременный ряд - условно сходящийся.